Mechanical Engineering Chapter 5 Homework The free-body diagram of the system is shown

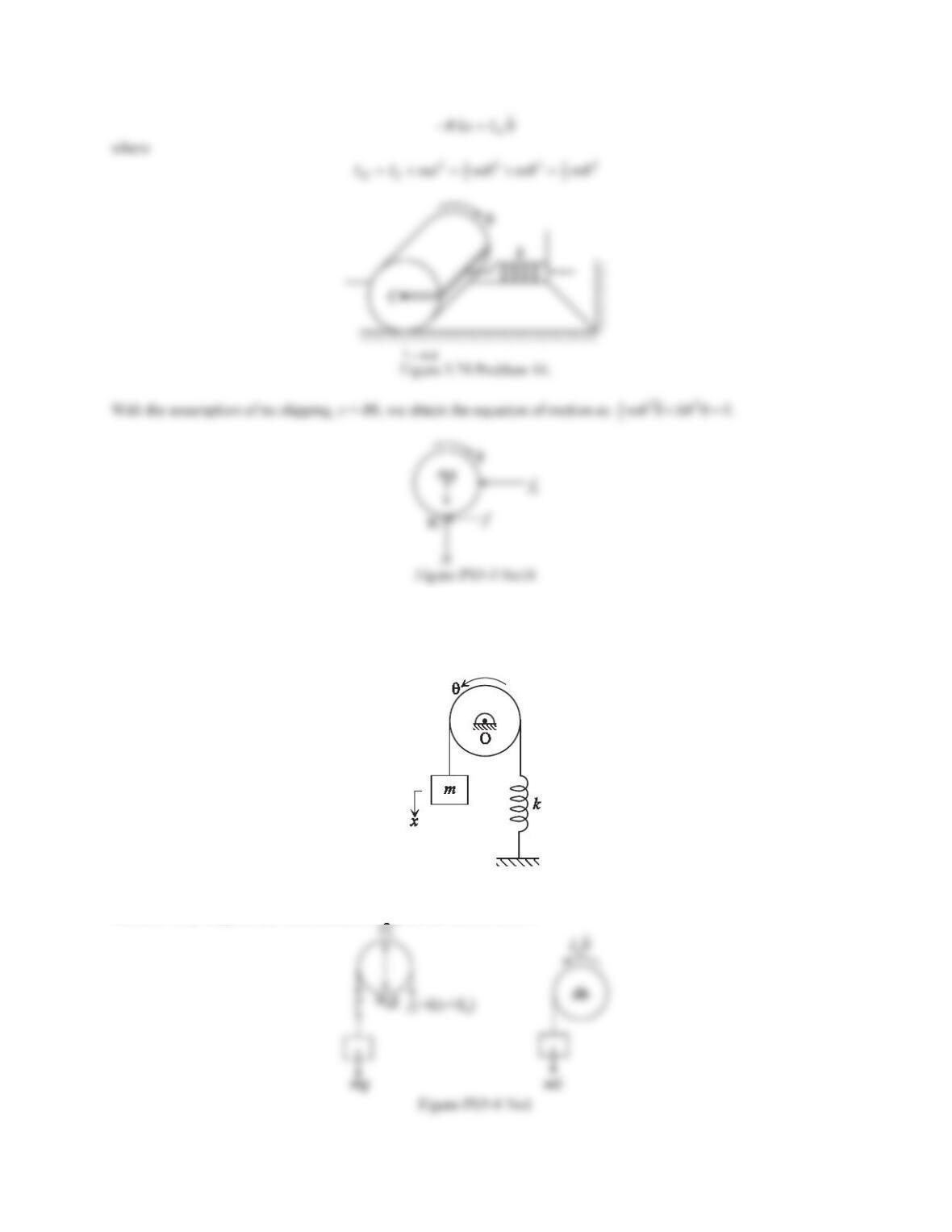
15. Consider the system shown in Figure 5.73, where a uniform sphere of mass mand radius rrolls along an

inclined plane of 30°. A translational spring of stiffness kis attached to the sphere. Assuming that there is no

slipping between the sphere and the surface, draw the necessary free-body diagram and derive the differential

equation of motion.

Figure 5.73 Problem 15.

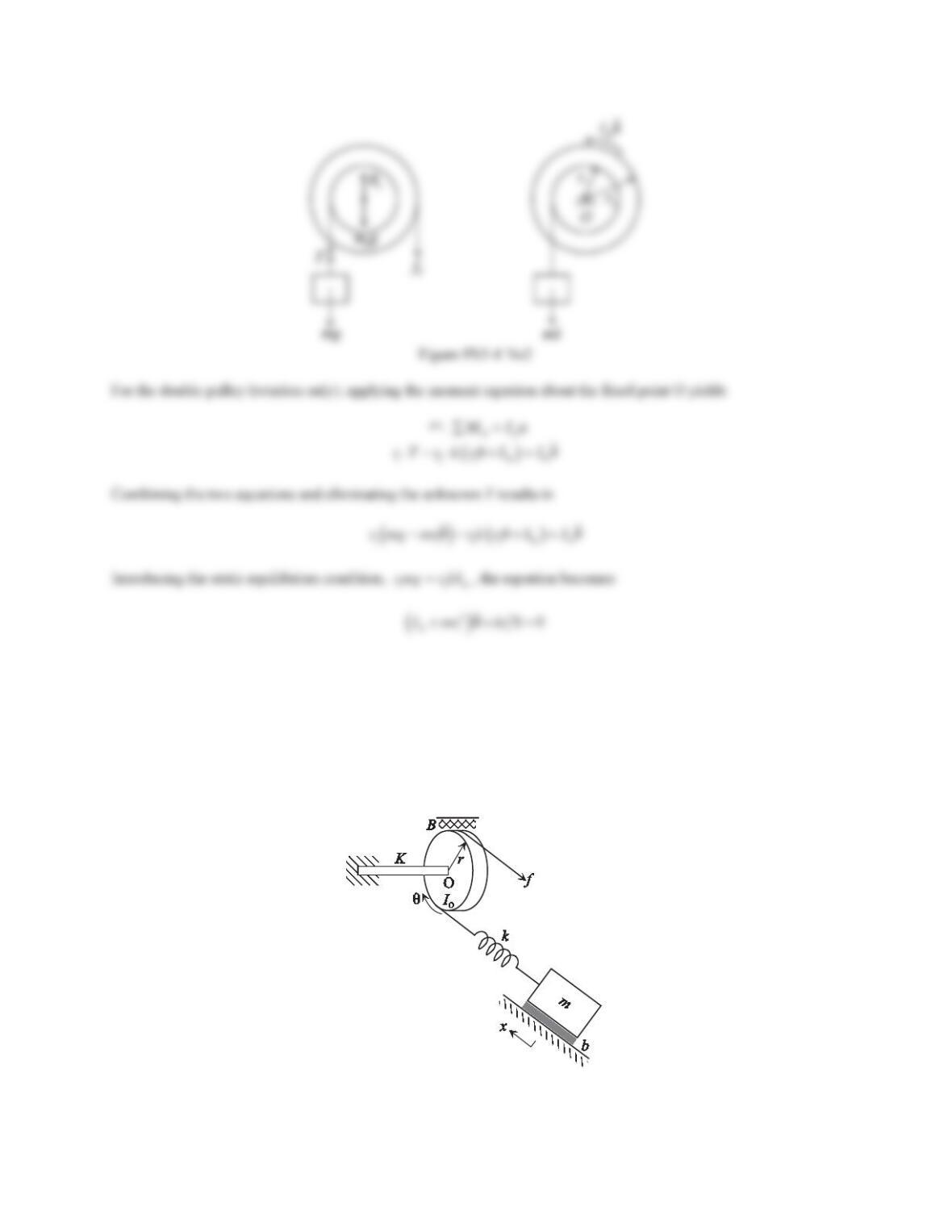
Solution

The free-body diagram of the system is shown in the figure below, where the normal force Nand the friction force f

are reaction forces at the contact point. Assuming that the sphere rolls down the incline, the spring is in compression

and fkis the spring force. When the sphere is at the static equilibrium position, we have fk=kįst ZKHUHįst is the

static deformation of the spring. Then,

16. Consider the system shown in Figure 5.74. A uniform solid cylinder of mass m, radius R, and length Lis fitted

with a frictionless axle along the cylinder’s long axis. A spring of stiffness kis attached to a bracket connected

to the axle. Assume that the cylinder rolls without slipping on a horizontal surface. Draw the necessary free-

body diagram and derive the differential equation of motion.

Solution

The free-body diagram of the system is shown, where the normal force Nand the friction force fare reaction forces

at the contact point. When the cylinder is at the static equilibrium position, Gst = 0, where Gst is the static deformation

175

Problem Set 5.4

1. For the pulley system in Example 5.14, draw the free-body diagram and kinematic diagram, and derive the

equation of motion using the force/moment approach.

Figure 5.82 A pulley system.

Solution

The free-body diagram and the kinematic diagram are shown below.

176

2. The double pulley system shown in Figure 5.86 has an inner radius of r1and an outer radius of r2. The mass

moment of inertia of the pulley about point O is IO. A translational spring of stiffness kand a block of mass m

are suspended by cables wrapped around the pulley as shown. Draw the free-body diagram and kinematic

diagram, and derive the equation of motion using the force/moment approach.

Figure 5.86 Problem 2.

Solution

The free-body diagram and the kinematic diagram are shown below.

At static equilibrium, we have

st

į

k

fk

and

177

3. Consider the mechanical system shown in Figure 5.87. A disk-shaft system is connected to a block of mass m

through a translational spring of stiffness k. The elasticity of the shaft and the fluid coupling are modeled as a

torsional spring of stiffness Kand a torsional viscous damper of damping coefficient B, respectively. The radius

of the disk is rand its mass moment of inertia about point O is IO. Assume that the friction between the block

and the horizontal surface cannot be ignored and is modeled as a translational viscous damper of damping

coefficient b. The input to the system is the force f. Draw the necessary free-body diagram and the kinematic

diagram, and derive the equations of motion.

Figure 5.87 Problem 3.

178

Solution

This is a mixed system, where the mass block undergoes translational motion along x-direction and the motion of the

disk is pure rotation about point O that is fixed. Choose the displacement of the block xand the angular

displacement of the disk șDVWKHJHQHUDOL]HGFRRUGLQDWHVAssuming that the block and the disk are displaced in their

4. Consider the mechanical system shown in Figure 5.88, where the motion of the rod is small angular rotation.

When T= 0 and f= 0, the deformation of each spring is zero and the system is at static equilibrium. Assume that

the friction between the block of mass m1and the horizontal surface cannot be ignored and is modeled as a

translational viscous damper of damping coefficient b.

a. Assuming that a>c> 0, determine the mass moment of inertia of the rod about the pivot point O.

b. Draw the necessary free-body diagram and the kinematic diagram, and derive the equations of motion for

small angles.

Figure 5.88 Problem 4.

179

Solution

a. The mass moment of inertia of the rod about point O can be found by applying the parallel axis theorem



2

22 22

111

OC 12 2 3

() () ( )IIMd MacMa ac Macac      

5. Consider the mechanical system shown in Figure 5.89, where a simple pendulum is pivoted on a cart of mass m.

The pendulum consists of a point mass Mconcentrated at the tip of a massless rod of length L. Assume that the

pendulum is constrained to rotate in a vertical plane, and the cart moves on a smooth horizontal surface. Denote

the displacement of the cart as xDQGWKHDQJXODUGLVSODFHPHQWRIWKHSHQGXOXPDVș‘UDZWKHQHFHVVDU\IUHH–

body diagram and kinematic diagram, and derive the equations of motion for small angles.

Figure 5.89 Problem 5.

Solution

The free-body diagram and the kinematic diagram are shown in the figure below.

6. Consider the mechanical system shown in Figure 5.90. Draw the necessary free-body diagram and kinematic

diagram, and derive the equations of motion for small angles.

Figure 5.90 Problem 6.

Solution

The free-body diagram and the kinematic diagram are shown in the figure below. Applying the force equation to the

whole system along the x-direction gives



2

1

:

xiCi

x

i

xF ma

o ¦ ¦

7. Consider the mechanical system shown in Figure 5.91. The inputs are the force f1applied to the cart and the

force f2applied at the tip of the rod. The outputs are the displacement xof the cart and the angular displacement

șRIWKHSHQGXOXP

a. Draw the free-body diagram and kinematic diagram, and derive the equations of motion for small angles.

b. Using the differential equation obtained in Part (a), determine the state-space representation.

182

Figure 5.91 Problem 7.

Solution

a. The free-body diagram and the kinematic diagram are shown in the figure below.

Applying the force equation to the whole system along the x-direction gives

183

b. The state, the input, and the output are specified as

1

21

32

4

ș

xx

xf

x

xf

x

½½

°°°° ½ ½

°°°°

® ¾ ®¾ ® ¾ ®¾

¯¿

°°°°

¯¿

xuy



Thus, the state-space equation in matrix form is

11

0010 0 0

0001 0 0

xx

ªºªº

«»«»

½ ½



8. Consider the mechanical system shown in Figure 5.92. Draw the necessary free-body diagram and kinematic

diagram, and derive the equations of motion for small angles.

Figure 5.92 Problem 8.

184

Solution

The free-body diagram and the kinematic diagram are shown in the figure below. Applying the force equation to the

whole system along the x-direction gives



2

1

:

xiCi

x

i

xF ma

o ¦ ¦

2

11 2 2 22

șFRVș ș VLQș

LL

kx bx kx bx mx Mx M M      

 

   

9. For the mechanical system in Problem 2, use the energy method to derive the equation of motion.

Solution

The static equilibrium position and the deformed positions are shown in the figure below. At equilibrium, we have

12st

įrmg rk

. Assuming that the block and the pulley move along the direction shown gives

185

10. For the mechanical system in Problem 11 of Problem Set 5.3, use the energy method to derive the equation of

motion.

Solution

The system is only subjected to the gravitational and spring forces, and it is a conservative system. When ș , the

springs are at their free length. Assuming that the rod rotates along the positive direction by a small angle Tgives

2

1

O

2

șTI 

22

111

12

222

()cosșș ș

ge

VV V Mg ab ka kb     

186

11. Repeat Problem 5 using Lagrange’s equations.

Solution

The system is only subjected to the gravitational forces, and it is a conservative system.

187

12. Repeat Problem 6 using Lagrange’s equations.

Solution

The system is only subjected to the gravitational and spring forces, and it is a conservative system.

188

13. A robot arm consists of rigid links connected by joints allowing the relative motion of neighboring links. The

dynamic model for a robot arm can be derived using Lagrange’s equations

d,1,2,,

d

i

ii

i

TTV

in

t

§·

www

 W }

¨¸

wT wT

wT

©¹



ZKHUHșiis the angular displacement of the iWKMRLQWĲiis the torque applied to the ith joint, and nis the total

number of joints. Consider a single-link planar robot arm as shown in Figure 5.93. Use Lagrange’s equations to

derive the dynamic model of the robot arm. Assume that the motion of the robot arm is constrained in a vertical

plane, and the joint angle varies between 0° and 360°.

Figure 5.93 Problem 13.

Solution

The kinetic energy of the robot arm is

22222

111 1

O

223 6

ș ș șT I mL mL



189

14. Repeat Problem 13 for a two-link planar robot arm as shown in Figure 5.94. Assume that the motion of the

robot arm is constrained in a horizontal plane, and the joint angles vary between 0° and 360°.

Figure 5.94 Problem 14.

Solution

The motion of the robot arm is assumed to be constrained in a horizontal plane. Thus, the gravitational potential

energy does not change ( ș

i

Vww

) and the Lagrange’s equations can be rewritten as

190

Figure PS5-4 No14

191

Problem Set 5.5

1. Repeat Example 5.16, and determine a mathematical model for the simple one-degree-of-freedom system

shown in Figure 5.95DLQWKHIRUPRIDGLIIHUHQWLDOHTXDWLRQRIPRWLRQLQș2.

Solution

As shown in Example 5.16, the differential equation of motion in

1

ș

is

2

1

C1 C2 1 1

2

r

II

r

§·

T W

¨¸

©¹



Introducing the geometric constraint

21 12

rrTT

,the above differential equation can be rewritten as

2. Repeat Example 5.17, and determine a mathematical model for the single-link robot arm shown in Figure 5.96

LQWKHIRUPRIDGLIIHUHQWLDOHTXDWLRQRIPRWLRQLQWKHORDGYDULDEOHș

192

Solution

As shown in Example 5.17, the differential equation of motion in terms of the angular displacement of the motor is

22

mmm mm

()( )INI BNBT T W

 

3. Consider the one-degree-of-freedom system shown in Figure 5.98. The system consists of two gears of mass

moments of inertia I1and I2and radii r1and r2UHVSHFWLYHO\7KHDSSOLHGWRUTXHRQJHDULVĲ1. Assume that the

gears are connected with flexible shafts, which can be approximated as two torsional springs of stiffnesses K1

and K2, respectively.

a. Draw the necessary free-ERG\GLDJUDPVDQGGHULYHWKHGLIIHUHQWLDOHTXDWLRQRIPRWLRQLQș1.

b. 8VLQJWKHGLIIHUHQWLDOHTXDWLRQREWDLQHGLQ3DUWDGHWHUPLQHWKHWUDQVIHUIXQFWLRQĬ2(s)/T1(s).

c. Using the differential equation obtained in Part (a), determine the state–VSDFHUHSUHVHQWDWLRQZLWKș2as the

output.

Figure 5.98 Problem 3.

Solution

a. The free-body diagram is shown in the figure below. Applying the moment equation to each gear gives

+:

OO

ĮMI¦

Gear 1:

1111 11

Ĳș șKrFI



Gear 2:

22 2 22

șșKrFI 



193

4. Consider the gear–train system shown in Figure 5.99. The system consists of a rotational cylinder and a pair of

gears. The gear ratio is N=r1/r27KHDSSOLHGWRUTXHRQWKHF\OLQGHULVĲa. Assume that the gears are connected

with flexible shafts, which can be approximated as two torsional springs of stiffnesses K1and K2, respectively.

a. Draw the necessary free-body diagrams, and derive the differential equations of motion.