-30 -20 -10 010
-30
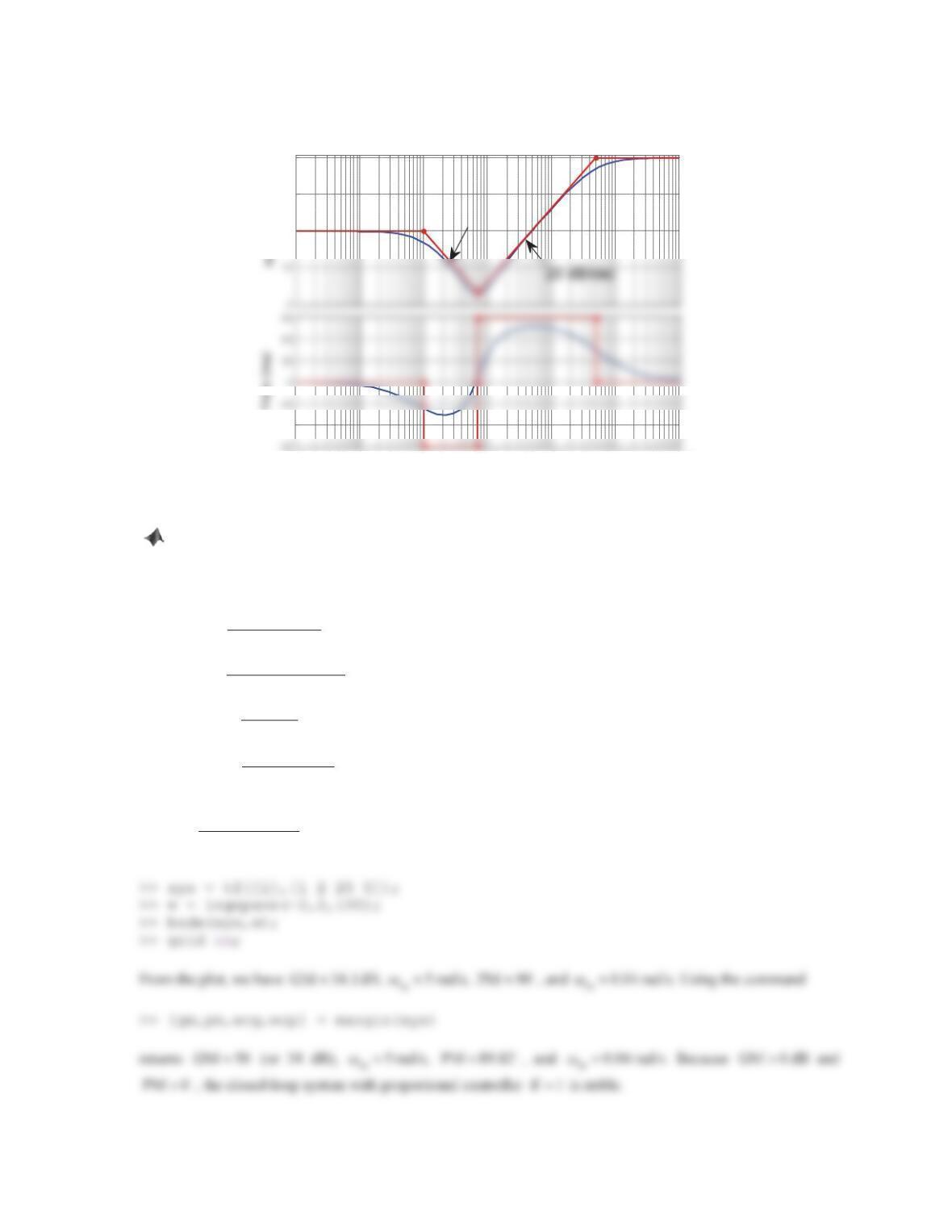
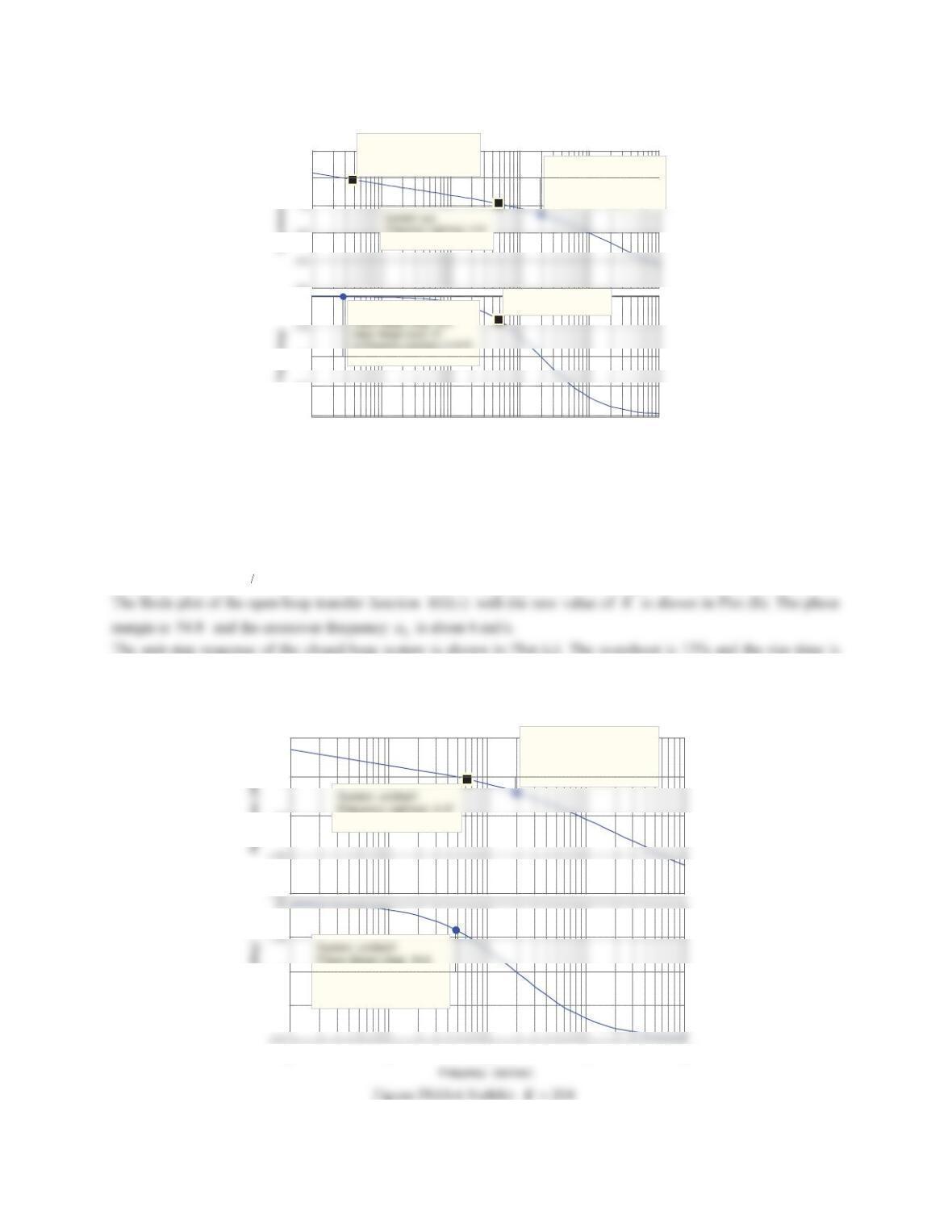
5. Figure 10.75 shows the Bode plot for an open-loop transfer function KG(s) with K= 500.
a. Determine the stability of the closed-loop system with K= 500.
b. Determine the value of Kthat would yield a PM of 45°.
Solution
a. As shown in the figure, the magnitude is 13 dB when the phase curve crosses
180D
. This implies that
GM 13 dB. The phase is
204D
when the magnitude curve crosses 0 dB. This implies that
PM 24 D
.
Because
GM 0
dB and
PM 0
D
, the closed-loop system with a proportional controller 500K is unstable.
b. To yield a phase margin of
45
D
, the phase when the magnitude plot crosses 0 dB should be
135
D
. It is
observed from the figure that the magnitude is 33 dB when the phase is
135
D
. To make the magnitude be 0
dB, the magnitude plot should slide downward by 33 dB. This is the effect of dividing by a constant term of
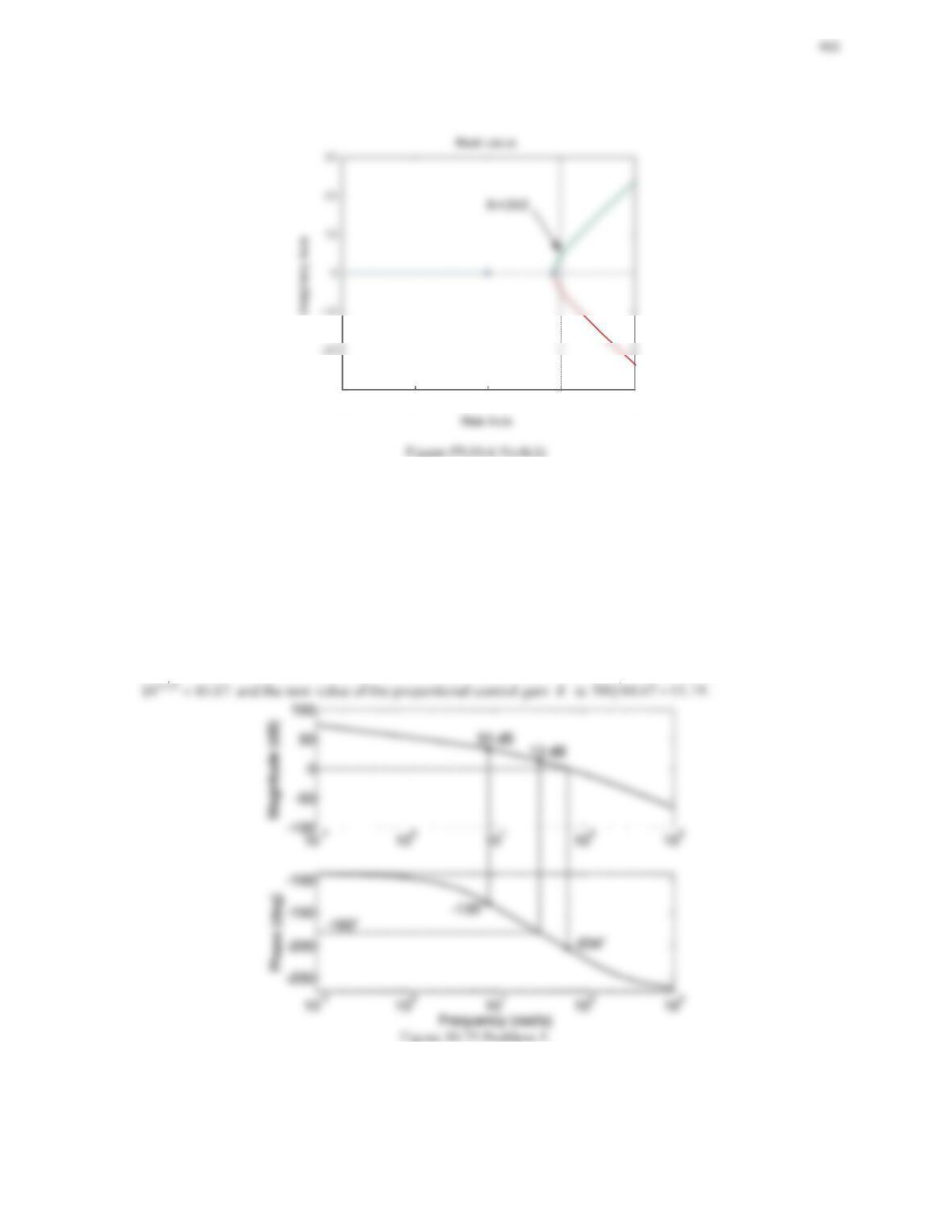
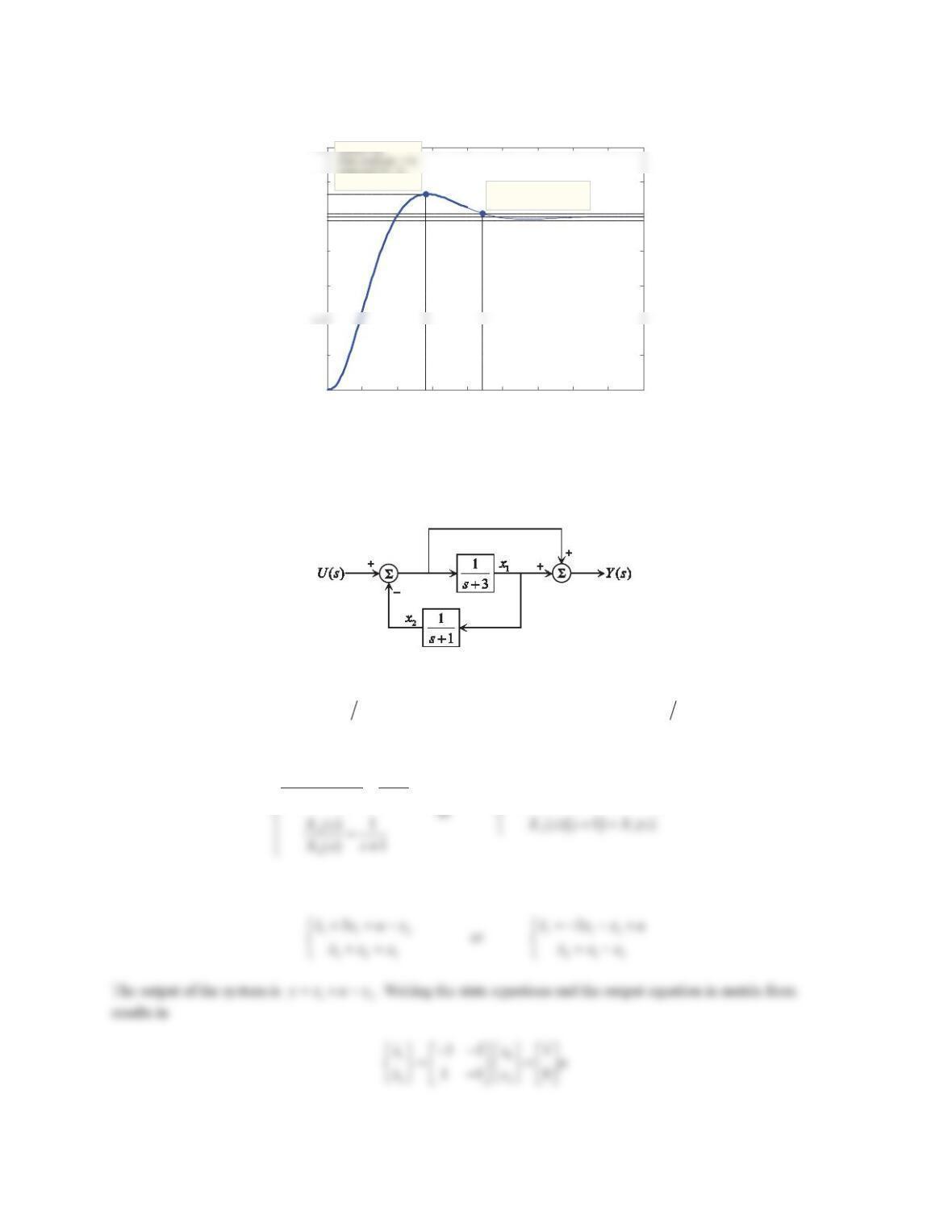
6. The Bode plot for an open-loop transfer function KG(s) is shown in Figure 10.76.
a. Determine the stability of the closed-loop system.