433
Problem Set 10.4
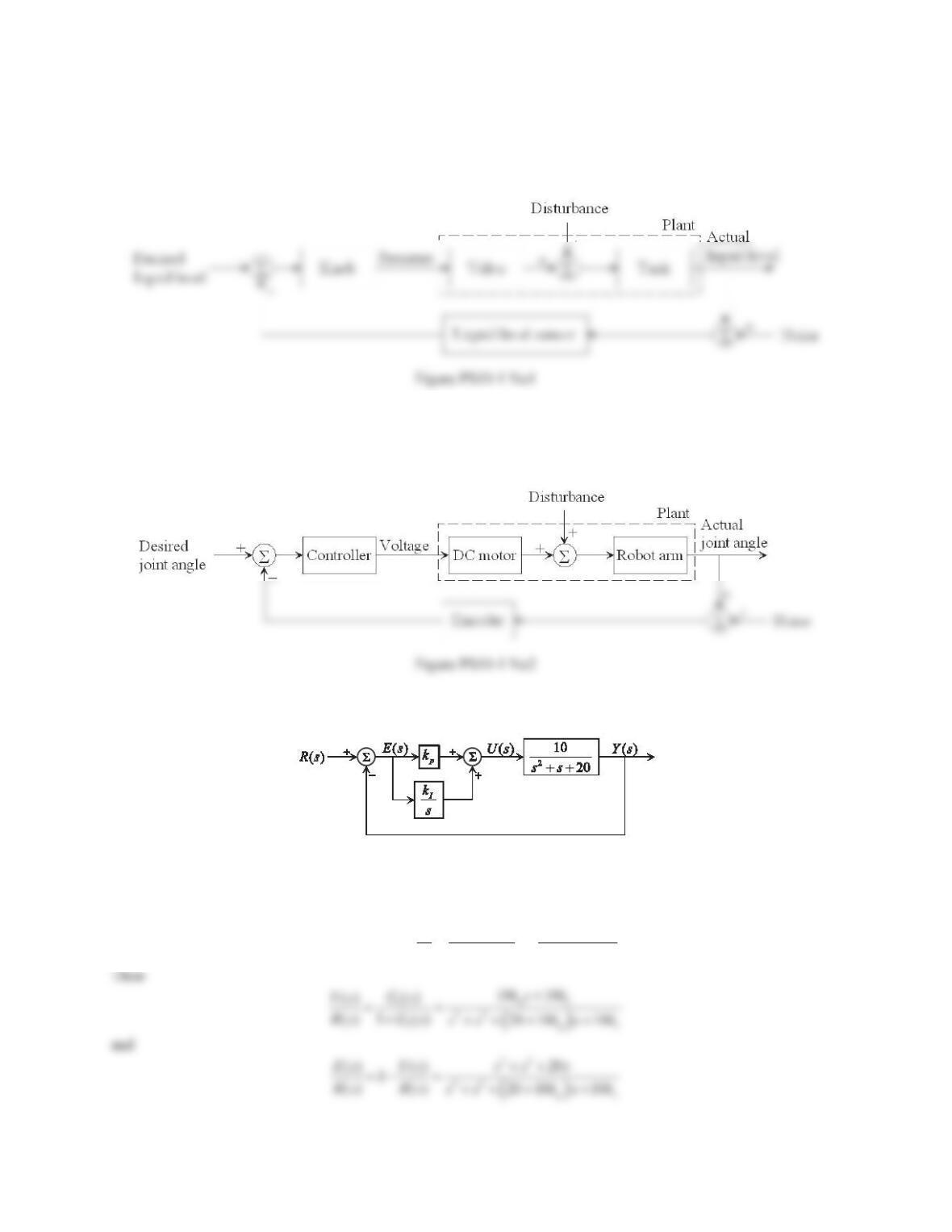
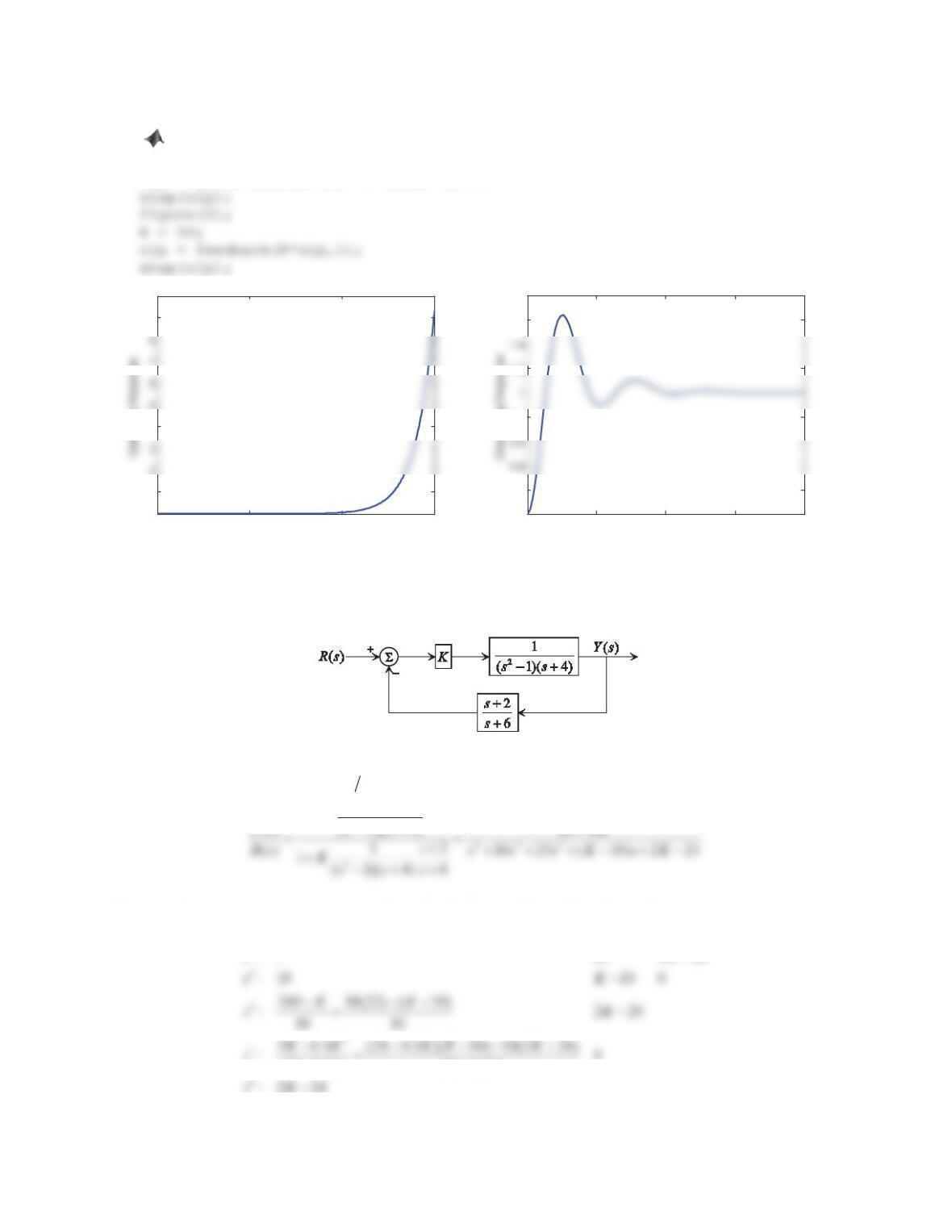
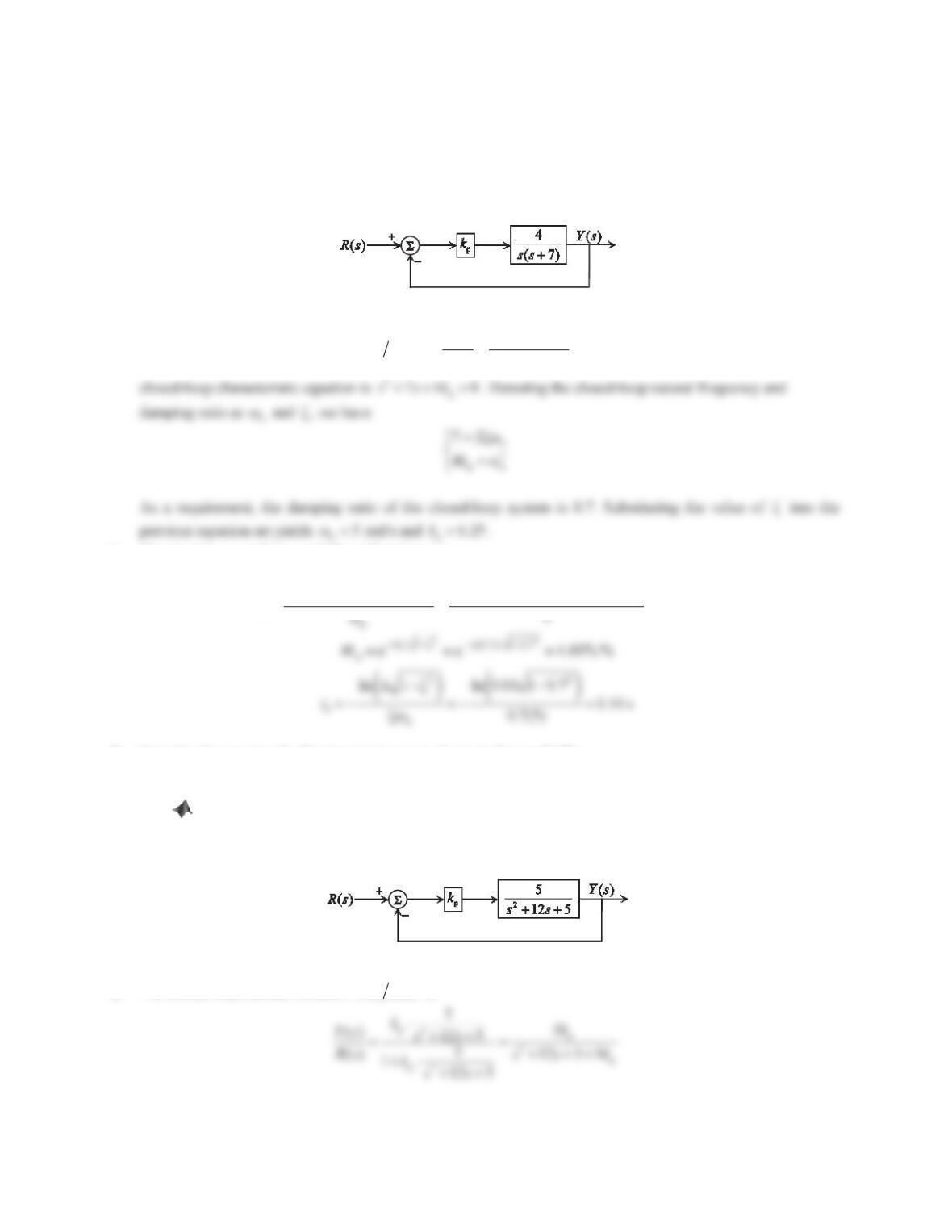
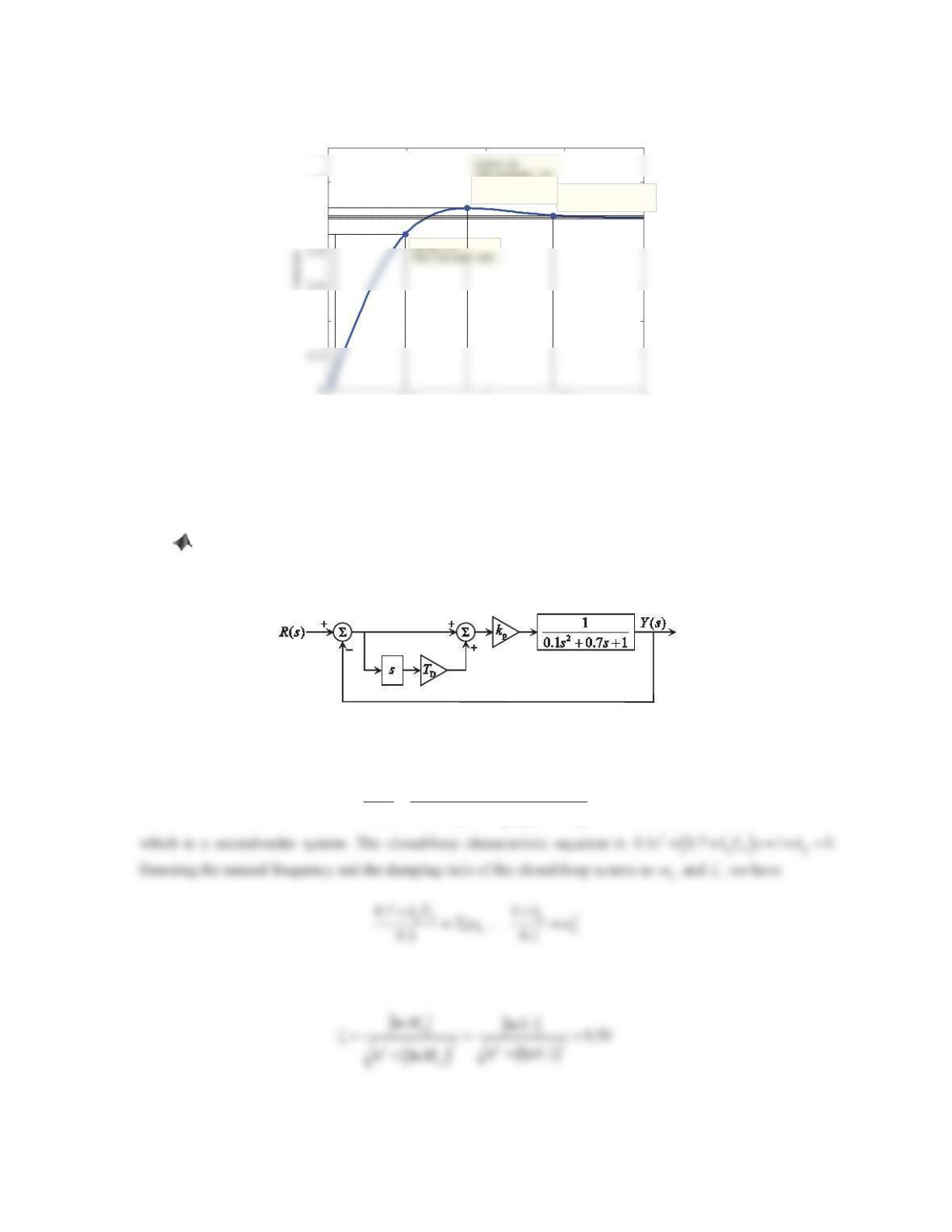
1. Figure 10.38 shows a negative feedback control system.
a. Design a P controller such that the damping ratio of the closed-loop system is 0.7.
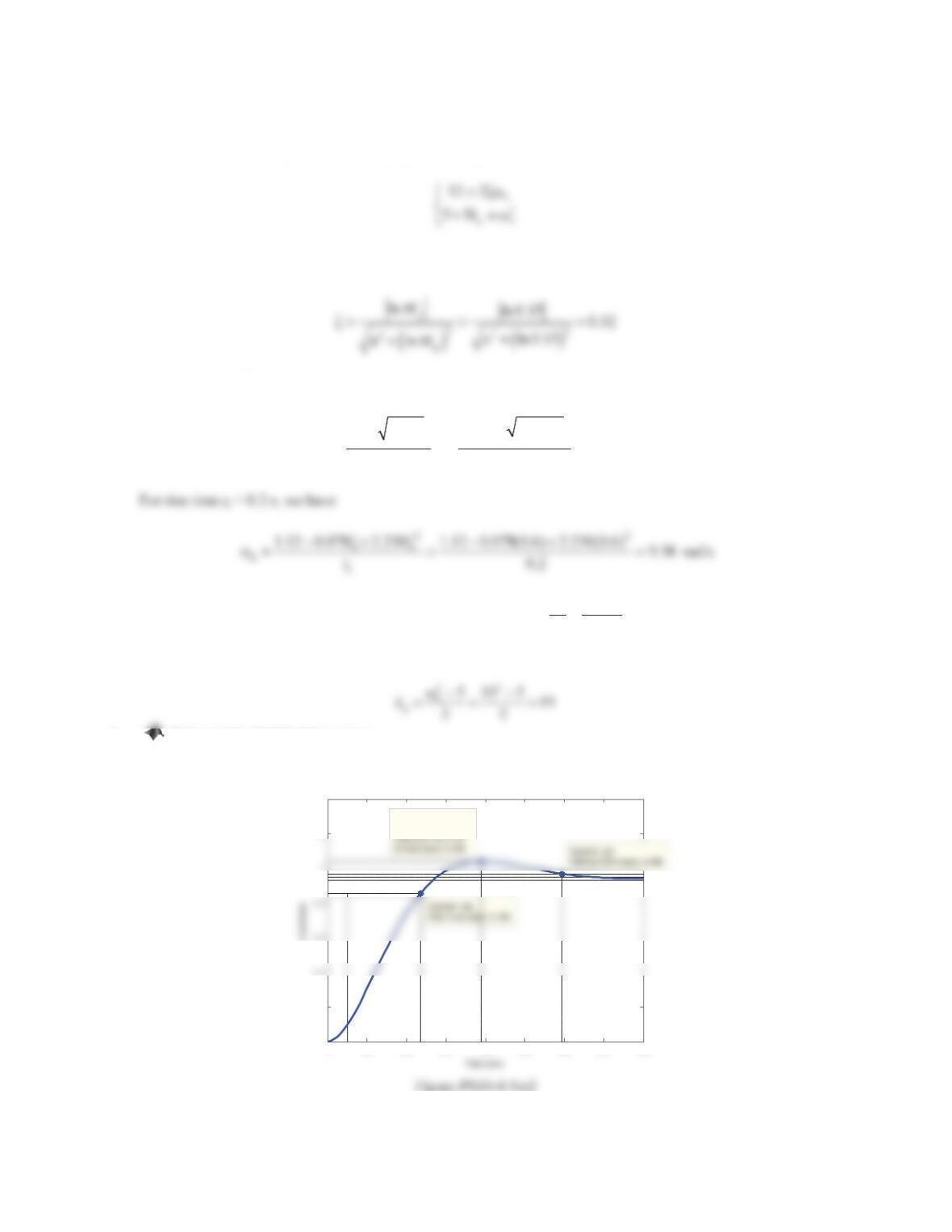
b. Estimate the rise time, overshoot, and 1% settling time in the unit-step response for the closed-loop system.
Figure 10.38 Problem 1.
Solution
a. The closed-loop transfer function () ()Ys Rs is
p
2
p
4
()
() 7 4
k
Ys
Rs s s k
, which is a second-order system. The
b. The rise time, overshoot, and 1% settling time are
22
r
1.12 0.078 2.230 1.12 0.078(0.7) 2.230(0.7) 0.43
t]]
|
s
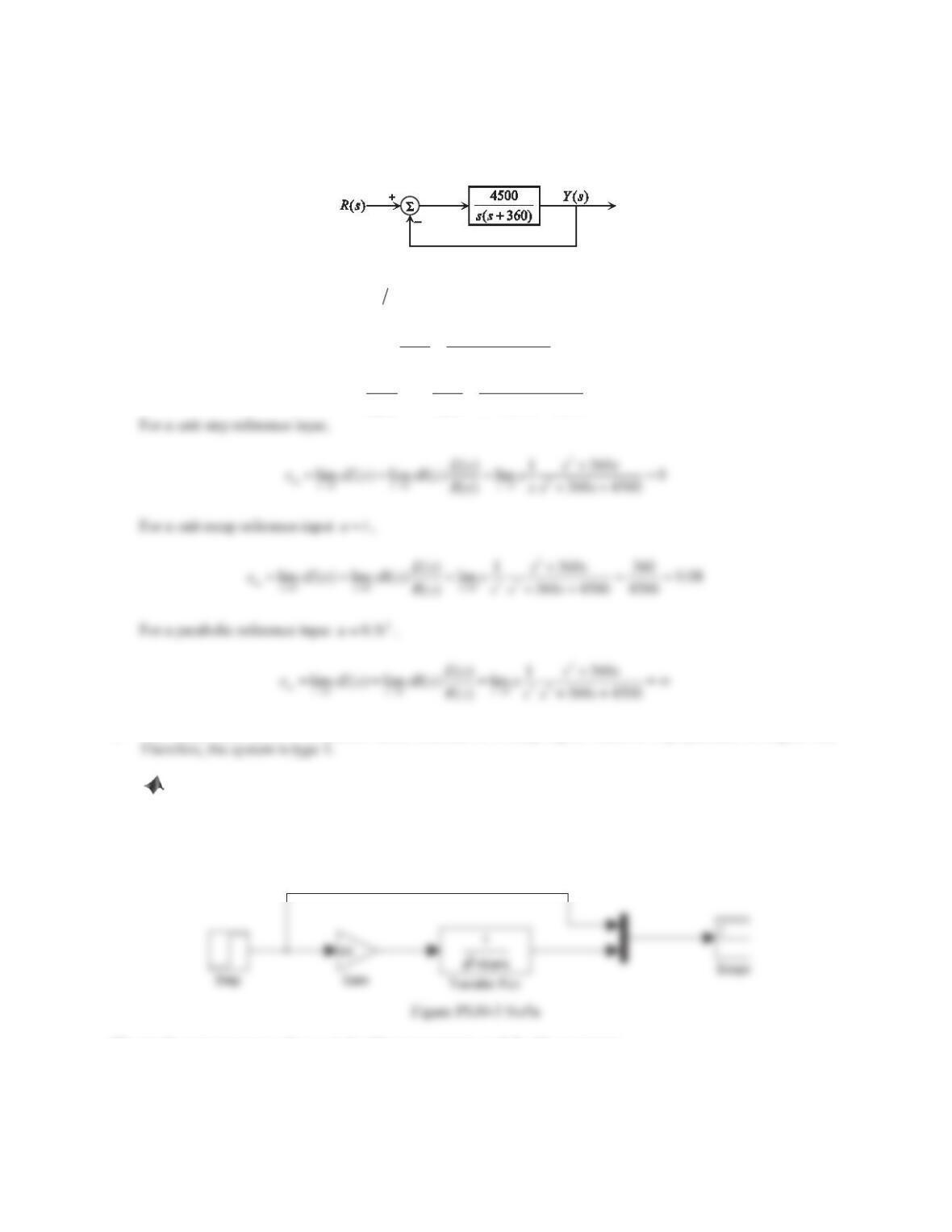
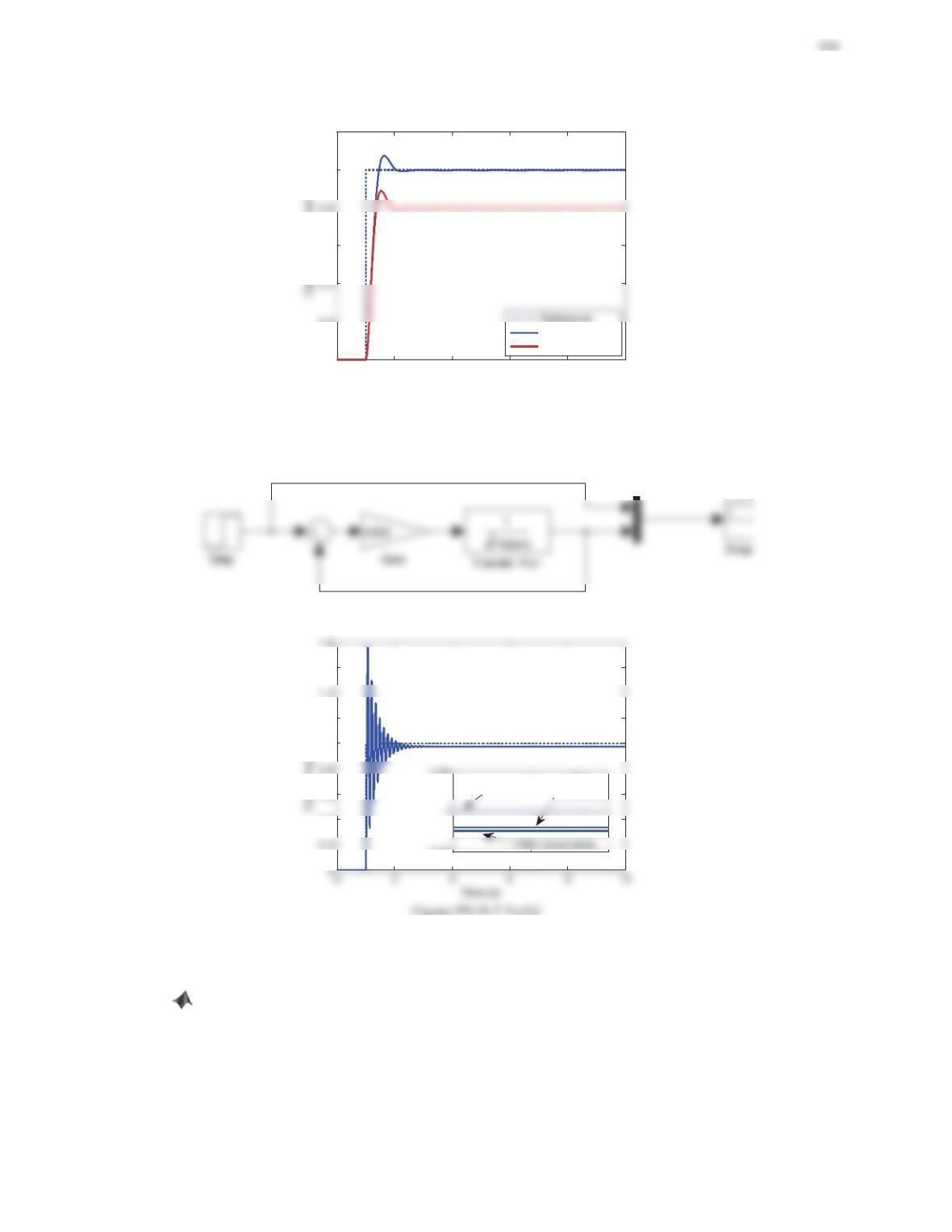
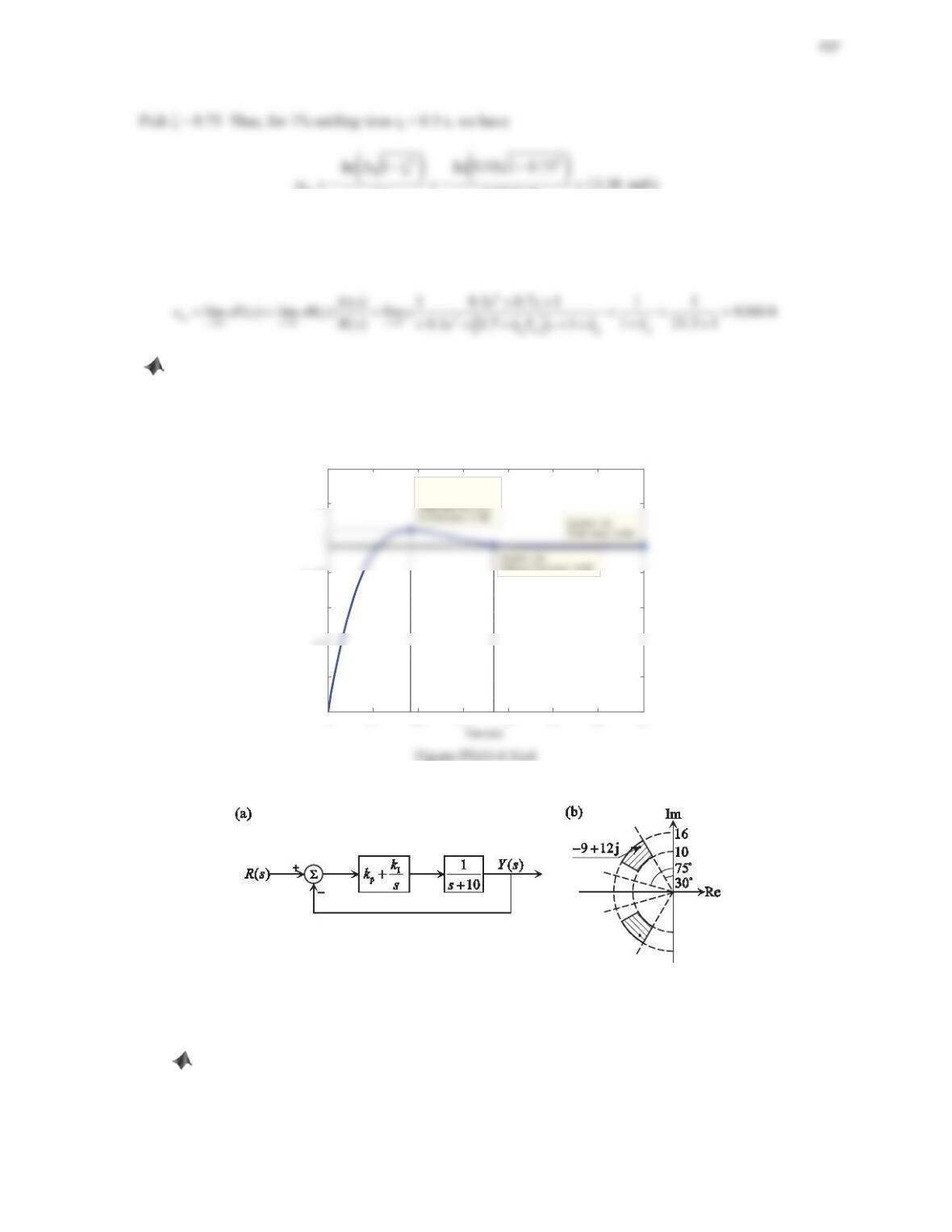
2. Consider the negative feedback control system shown in Figure 10.39.
a. Design a P controller such that the maximum overshoot in the response to a unit-step reference input is less
than 15%, the 2% settling time is less than 1 s, and the rise time is less than 0.2 s.
b. Use MATLAB to plot the unit-step response of the closed-loop system. Find the overshoot, 2%
settling time, and rise time. If the time-domain specifications exceed the requirements, make a fine tuning
and reduce them to be approximately the specified values or less.
Figure 10.39 Problem 2.
Solution
a. The closed-loop transfer function () ()Ys Rs is