297
Unit 12 Design Solutions
Solutions to Unit 12 Design and Simulation Problems
Problem 12.10 is a simulation exercise where students are required to design and simulate a counter. The problem has
14 parts of equal difculty, so that different students can be assigned different parts. We ask students to do the following
preparation and lab work:
1. Read Unit 12 in the course textbook, completing Study Guide parts 1 through 5.
3. Answer the following questions:
(a) How can a D ip-op be set to logic 0 without using the clock input?
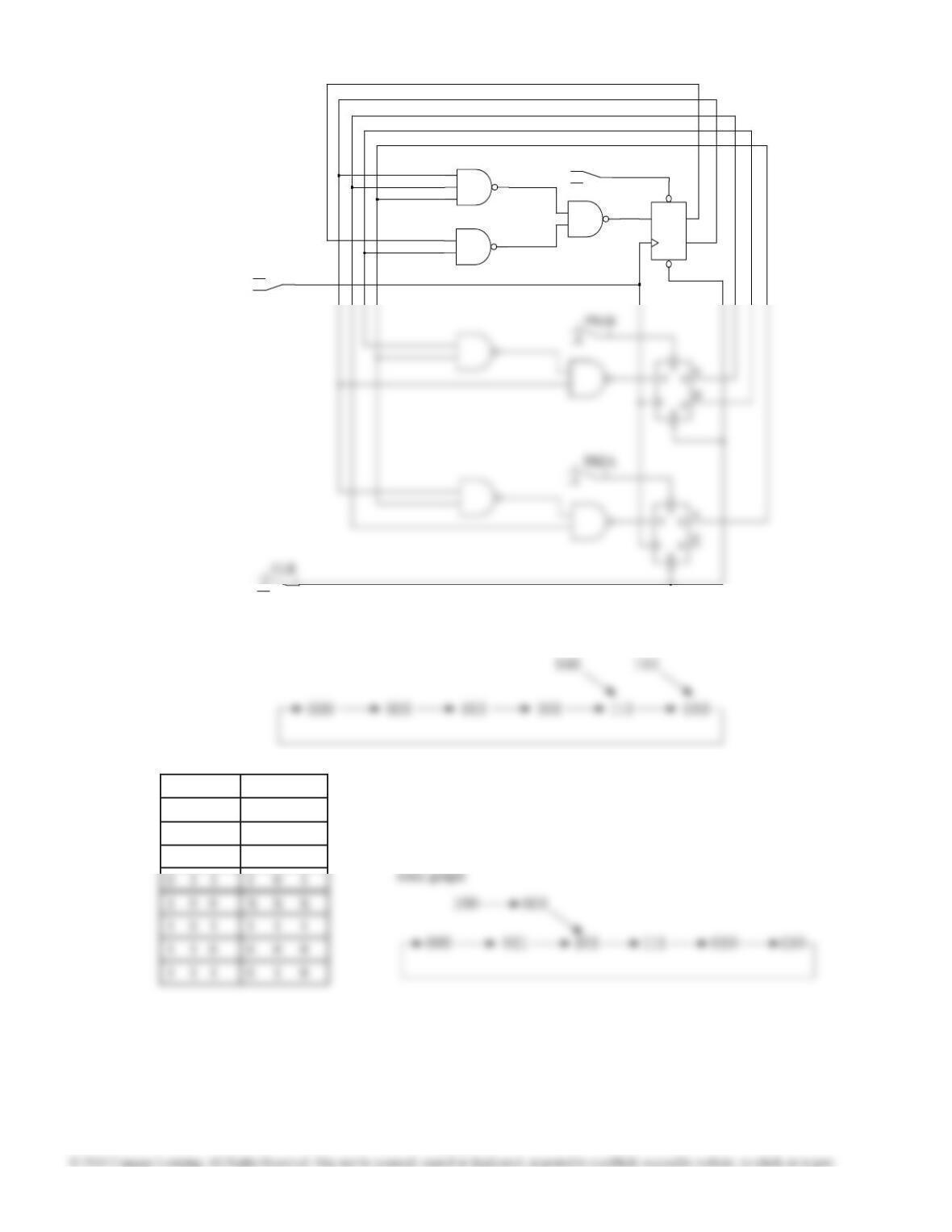
4. Design a counter that counts in the sequence assigned to you. Use D ip-ops, NAND gates, and inverters.
Draw your circuit explicitly showing all connections to gate and ip-op inputs. Explicitly means that you
should draw in all wires, don’t just label the inputs and outputs. Show switches connected to the Preset
and Clear inputs of the ip-ops. Use one switch for all clears and a separate switch for each preset.
5. Explain in detail how you can set the ip-ops to the two missing states not in the prescribed counting sequence
without using the clock input. Your explanation should describe each change you make to a switch position.
After you have cleared or set a ip-op, in what position (0 or 1) should you leave the switches?
C B A C+ B+ A+
0 0 0 0 0 1
0 0 1 0 1 1
0 1 0 0 0 0
C
B A 0 1
00
0
X
C
B A 0 1
00
0
X
C
B A 0 1
00
1
X
12.10(a)
298
Unit 12 Design Solutions
12.10(a)
(cont.)
S
D
RQ’
Q
C
C’
CLK
1
00
PREC
1
01
01
State graph determined experimentally:
12.10(b) C B A C+ B+ A+
0 0 0 0 1 1
0 0 1 X X X
0 1 0 1 1 0
*DC = C’B + B’A DC = C’B + C B’
*DB = C’A’ + C A *DA = B’ + C’A
Circuit based on equations marked * was used to obtain the following
299
Unit 12 Design Solutions
12.10(c) C B A C+ B+ A+
0 0 0 1 1 0
0 0 1 0 0 0
0 1 0 X X X
*DC = A’ + B *DB = C’A’ + B A’
*DA = C B’ + B A’ DA = C B’ + C A’
12.10(d) C B A C+ B+ A+
0 0 0 1 0 0
0 0 1 1 1 0
0 1 0 X X X
*DC = C’ + B’A + B A’ *DB = B’A
*DA = C B’ + B A’ DA = C B’ + C A’
12.10(e) C B A C+ B+ A+
0 0 0 0 1 0
0 0 1 X X X
DC = C’B + B A DB = C’ + B’
DA = C’B A’ + C A
Circuit based on equations marked * was used to obtain the following
Circuit based on equations marked * was used to obtain the following
12.10(f) C B A C+ B+ A+
0 0 0 1 0 0
0 0 1 1 1 1
0 1 0 X X X
DC = C’ + B DB = C’A + B A
DA = C’A + C A’
300
Unit 12 Design Solutions
12.10(g) C B A C+ B+ A+
0 0 0 0 1 0
0 0 1 1 1 0
0 1 0 1 1 1
DC = C’A + C’B + B A DB = C’
DA = C’B + C A
12.10(h) C B A C+ B+ A+
0 0 0 1 0 1
0 0 1 1 1 0
0 1 0 0 1 1
*DC = C’B’ *DB = B’A + C’B A’
*DA = C’B + C’A’ DA = C’B + B’A’
DA = C’A’ + B A
12.10(i) C B A C+ B+ A+
0 0 0 1 0 0
0 0 1 1 1 0
*DC = C’B’ + C B A’ *DB = C A’ + C’A
DB = C A’ + B’A *DA = B A’
12.10(j) C B A C+ B+ A+
0 0 0 0 0 1
0 0 1 1 1 1
DC = B’A + C’B A’ DB = B’A + B A’ + C
DA = B’ + C A’
301
Unit 12 Design Solutions
12.10(k) C B A C+ B+ A+
0 0 0 1 0 0
0 0 1 1 0 1
0 1 0 0 0 1
*DC = C’B’ + B’A *DB = C B’
*DA = B’A + B A’ DA = B’A + C’B
12.10(l) C B A C+ B+ A+
0 0 0 0 1 1
0 0 1 1 0 0
DC = A DB = C’A’ + B A
DA = C’A’ + C’B + B A’
12.10(m) C B A C+ B+ A+
0 0 0 1 0 0
0 0 1 X X X
0 1 0 0 1 1
DC = B’ + C A DB = B A’ + C
DA = C’B A’ + C B’
Circuit based on equations marked * was used to obtain the following
12.10(n) C B A C+ B+ A+
0 0 0 0 1 1
0 0 1 X X X
0 1 0 1 0 0
DC = C’B + A DB = C’B’ + A + C B
DA = C’B’ + C’A
302
Unit 12 Design Solutions