Aeronautical Engineering Chapter 5 Homework Problem When The Fluid Exiting Nozzle

Problem 5.C1

Estimating pipe wall friction is one of the most common tasks in fluids engineering. For long

circular, rough pipes in turbulent flow, wall shear



w is a function of density



, viscosity



, average

velocity V, pipe diameter d, and wall roughness height



. Thus, functionally, we can write



w = fcn(



,



, V, d,



). (a) Using dimensional analysis, rewrite this function in dimensionless form.

(b) A certain pipe has d = 5 cm and



= 0.25 mm. For flow of water at 20C, measurements show

the following values of wall shear stress:

Q (in gal/min)

~

1.5

3.0

6.0

9.0

12.0

14.0



w (in Pa)

~

0.05

0.18

0.37

0.64

0.86

1.25

Plot this data in the dimensionless form obtained in part (a) and suggest a curve-fit formula. Does

your plot reveal the entire functional relation obtained in part (a)?

Solution 5.C1

(a) There are 6 variables and 3 primary dimensions, therefore we expect 3 Pi groups. The

traditional choices are:

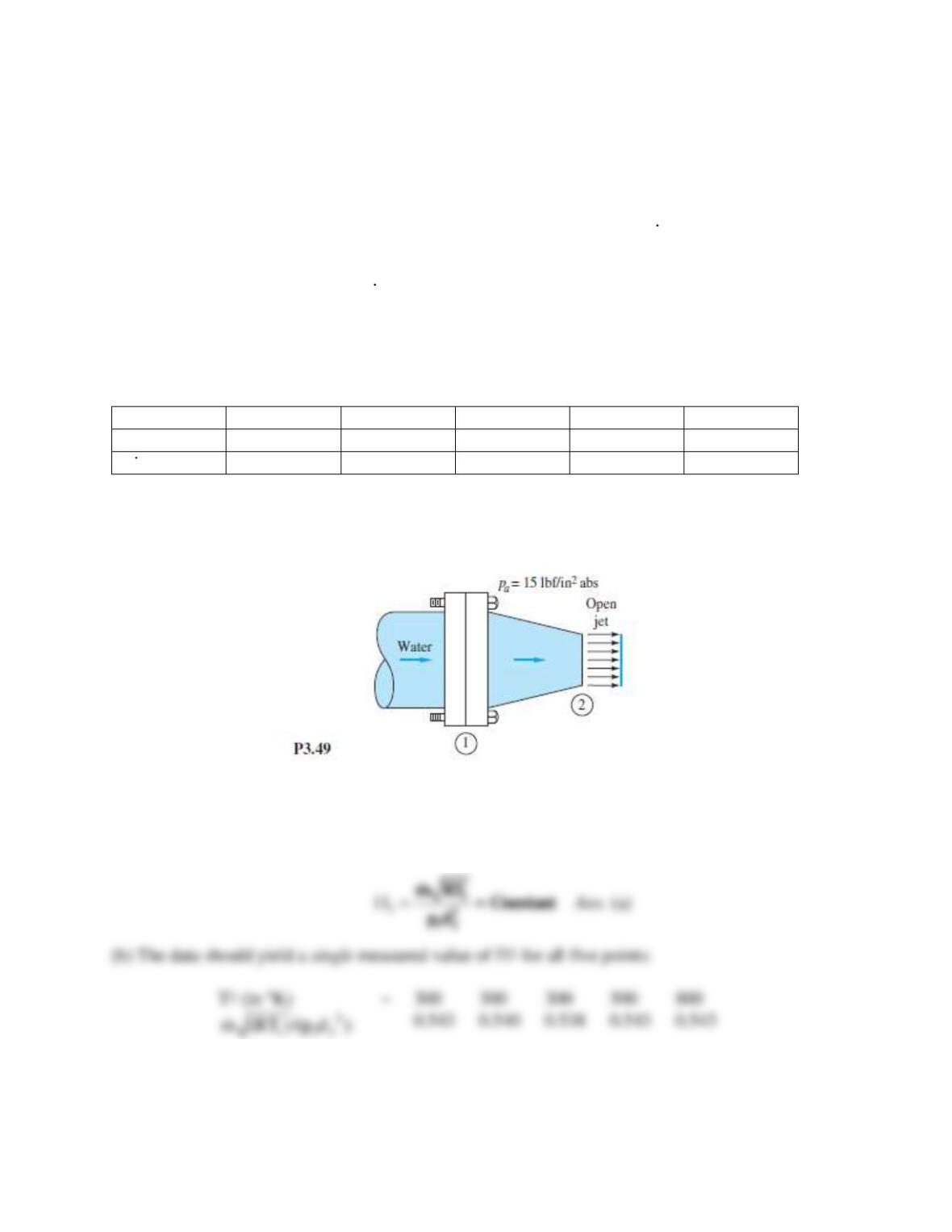
Problem 5.C2

When the fluid exiting a nozzle, as in Fig. P3.49, is a gas, instead of water, compressibility may be

important, especially if upstream pressure p1 is large and exit diameter d2 is small. In this case,

the difference p1 − p2 is no longer controlling, and the gas mass flow,

m,

reaches a maximum

value that depends upon p1 and d2 and also upon the absolute upstream temperature, T1, and the

gas constant, R. Thus, functionally,

=1 2 1

m fcn(p , d , T , R)

.

(a) Using dimensional analysis, rewrite this

function in dimensionless form. (b) A certain pipe has d2 = 1 cm. For flow of air, measurements

show the following values of mass flow through the nozzle:

T1 (in K)

300

500

800

p1 (in kPa)

200

250

300

m

(in kg/s)

0.037

0.046

0.055

0.043

0.034

Plot this data in the dimensionless form obtained in part (a). Does your plot reveal the entire

functional relation obtained in part (a)?

Solution 5.C2

(a) There are n = 5 variables and j = 4 dimensions (M, L, T, ), hence we expect only

n

−

j = 5 − 4 = 1 Pi group, which turns out to be

Problem 5.C3

Reconsider the fully developed draining vertical oil film problem (see Fig. P4.80) as an exercise in

dimensional analysis. Let the vertical velocity be a function only of distance from the plate, fluid

properties, gravity, and film thickness. That is, w = fcn(x,



,



, g,



).

(a) Use the pi theorem to rewrite this function in terms of dimensionless parameters.

(b) Verify that the exact solution from Prob. 4.80 is consistent with your result in part (a).

Solution 5.C3

There are n = 6 variables and j = 3 dimensions (M, L, T), hence we expect only

Problem 5.C4

The Taco Inc. Model 4013 centrifugal pump has an impeller of diameter D = 12.95 in. When pumping

20C water at  = 1160 rev/min, the measured flow rate Q and pressure rise p are given by the

manufacturer as follows:

Q (gal/min)

~

200

300

400

500

600

700

p (lb/in2)

~

36

35

34

32

29

23

(a) Assuming that p = fcn(



, Q, D, ), use the pi theorem to rewrite this function in terms of

dimensionless parameters and then plot the given data in dimensionless form. (b) It is desired to

use the same pump, running at 900 rev/min, to pump 20C gasoline at 400 gal/min. According to

your dimensionless correlation, what pressure rise p is expected, in lbf/in2?

Solution 5.C4

There are n = 5 variables and j = 3 dimensions (M, L, T), hence we expect

Problem 5.C5

Does an automobile radio antenna vibrate in resonance due to vortex shedding? Consider an antenna

of length L and diameter D. According to beam-vibration theory [see [34] or [35, p.401]] , the first

mode natural frequency of a solid circular cantilever beam is



n = 3.516[EI/(



AL4)]1/2, where E is

the modulus of elasticity, I is the area moment of inertia,



is the beam material density, and A is the

beam cross-section area. (a) Show that



n is proportional to the antenna radius R. (b) If the antenna

is steel, with L = 60 cm and D = 4 mm, estimate the natural vibration frequency, in Hz. (c)

Compare with the shedding frequency if the car moves at 65 mi/h.

Solution 5.C5

(a) From Fig. 2.13 for a circular cross-section, A =



R2 and I =



R4/4. Then the natural

frequency is predicted to be:

Problem 5.W1

In 98 percent of data analysis cases, the “reducing factor” j , which lowers the number n of

dimensional variables to n − j dimensionless groups, exactly equals the number of relevant

dimensions ( M , L , T , Q ). In one case (Example 5.5) this was not so. Explain in words why

this situation happens.

Solution 5.W1

Problem 5.W2

Consider the following equation: 1 dollar bill ≈ 6 in. Is this relation dimensionally inconsistent?

Does it satisfy the PDH? Why?

Solution 5.W2

Problem 5.W3

In making a dimensional analysis, what rules do you follow for choosing your scaling variables?

Solution 5.W3

Problem 5.W4

In an earlier edition, the writer asked the following question about Fig. 5.1: “Which of the three

graphs is a more effective presentation?” Why was this a dumb question?

Solution 5.W4

Problem 5.W5

This chapter discusses the difficulty of scaling Mach and Reynolds numbers together (an

airplane) and Froude and Reynolds numbers together (a ship). Give an example of a flow that

would combine Mach and Froude numbers. Would there be scaling problems for common

fluids?

Solution 5.W5

Problem 5.W6

What is different about a very small model of a weir or dam (Fig. P5.32) that would make the

test results difficult to relate to the prototype?

Solution 5.W6

Problem 5.W7

What else are you studying this term? Give an example of a popular equation or formula from

another course (thermodynamics, strength of materials, or the like) that does not satisfy the

principle of dimensional homogeneity. Explain what is wrong and whether it can be modified to

be homogeneous.

Solution 5.W7

Problem 5.W8

Some colleges (such as Colorado State University) have environmental wind tunnels that can be

used to study phenomena like wind flow over city buildings. What details of scaling might be

important in such studies?

Solution 5.W8

The solution to this word problem is not provided.

Problem 5.W9

If the model scale ratio is α = Lm/Lp , as in Eq. (5.31), and the Weber number is important, how

must the model and prototype surface tension be related to α for dynamic similarity?

Solution 5.W9

Problem 5.W10

For a typical incompressible velocity potential analysis in Chap. 8 we solve

20



=

, subject to

known values of

/n





on the boundaries. What dimensionless parameters govern this type of

motion?

Solution 5.W10

Problem 5.1

For axial flow through a circular tube, the Reynolds number for transition to turbulence is

approximately 2300 [see Eq. (6.2)], based upon the diameter and average velocity. If d = 5 cm and

the fluid is kerosene at 20C, find the volume flow rate in m3/h which causes transition.

Solution 5.1

For kerosene at 20C, take



= 804 kg/m3 and



= 0.00192 kg/ms. The only unknown in the

Problem 5.2

A prototype automobile is designed for cold weather in Denver, CO (-10C, 83 kPa). Its drag

force is to be tested in on a one-seventh-scale model in a wind tunnel at 150 mi/h and at 20C

and 1 atm. If model and prototype satisfy dynamic similarity, what prototype velocity, in mi/h,

is matched? Comment on your result.

Solution 5.2

First assemble the necessary air density and viscosity data:

Problem 5.3

The transfer of energy by viscous dissipation is dependent upon viscosity



, thermal conductivity

k, stream velocity U, and stream temperature To. Group these quantities, if possible, into the

dimensionless Brinkman number, which is proportional to



.

Solution 5.3

Here we have only a single dimensionless group. List the dimensions, from Table 5.1:

Problem 5.4

The transfer of energy by viscous dissipation is dependent upon viscosity



, thermal conductivity

k, stream velocity U, and stream temperature To. Group these quantities, if possible, into the

dimensionless Brinkman number, which is proportional to



.

Solution 5.4

For water at 20C take



 998 kg/m3 and



 0.001 kg/ms. For sea-level standard air take

Problem 5.5

An automobile has a characteristic length and area of 8 ft and 60 ft2, respectively. When tested in

sea-level standard air, it has the following measured drag force versus speed:

V, mi/h: 20 40 60

Drag, lbf: 31 115 249

The same car travels in Colorado at 65 mi/h at an altitude of 3500 m. Using dimensional analysis,

estimate (a) its drag force and (b) the horsepower required to overcome air drag.

Solution 5.5

For sea-level air in BG units, take



 0.00238 slug/ft3 and



 3.72E−7 slug/ft·s. Convert

the raw drag and velocity data into dimensionless form:

Problem 5.6

The disk-gap-band parachute in the chapter-opener photo had a drag of 1600 lbf when tested at

15 mi/h in air at 20ºC and 1 atm. (a) What was its drag coefficient? (b) If, as stated, the drag on

Mars is 65,000 lbf and the velocity is 375 mi/h in the thin Mars atmosphere, ρ ≈ 0.020 kg/m3,

what is the drag coefficient on Mars? (c) Can you explain the difference between (a) and (b)?

Solution 5.6

(a) Convert to SI units: 1600 lbf = 7117 N, 15 mi/h = 6.71 m/s, 51 ft = 15.5 m. For air at 20ºC

and 1 atm, take ρ ≈ 1.20 kg/m3. Compute the drag coefficient in the wind tunnel:

Problem 5.7

A body is dropped on the moon (g = 1.62 m/s2) with an initial velocity of 12 m/s. By using option-

2 variables, Eq. (5.11), the ground impact occurs at

** 0.34t=

and

** 0.84.S=

Estimate (a) the

initial displacement, (b) the final displacement, and (c) the time of impact.

Solution 5.7

(a) The initial displacement follows from the “option 2” formula, Eq. (5.12):

Problem 5.8

The Archimedes number, Ar, used to analyze flow of stratified fluids, is a dimensionless

combination of gravity g, density difference Δρ, fluid width H, and viscosity μ. Find the form of

this number if it is proportional to g.

Solution 5.8

Write the dimensions of the variables, from Table 5.1:

Problem 5.9

The Richardson number, Ri, which correlates the production of turbulence by buoyancy, is a

dimensionless combination of the acceleration of gravity g, the fluid temperature To, the local

temperature gradient T/z, and the local velocity gradient u/z. Determine the form of the

Richardson number if it is proportional to g.

Solution 5.9

In the {MLT} system, these variables have the dimensions {g} = {L/T2}, {To} = {},

Problem 5.10

Determine the dimension {MLT} of the following quantities:

22

0

1

(a) (b) ( ) (c) (d)

p

u T u

u p p dA c dx dy dz

x x y t

  

  

   

−

 

All quantities have their standard meanings; for example,



is density, etc.

Solution 5.10

Problem 5.11

During World War II, Sir Geoffrey Taylor, a British fluid dynamicist, used dimensional analysis

to estimate the wave speed of an atomic bomb explosion. He assumed that the blast wave radius

R was a function of energy released E, air density



, and time t. Use dimensional analysis to

show how wave radius must vary with time.

Solution 5.11

The proposed function is R = f(E,



, t). There are four variables (n = 4) and three primary

dimensions (MLT, or j = 3), thus we expect n-j = 4-3 = 1 pi group. List the dimensions:

Problem 5.12

The Stokes number, St, used in particle dynamics studies, is a dimensionless combination of five

variables: acceleration of gravity g , viscosity μ , density ρ , particle velocity U , and particle

diameter D . ( a ) If St is proportional to μ and inversely proportional to g , find its form .

(b) Show that St is actually the quotient of two more traditional dimensionless groups.

Solution 5.12

Problem 5.13

The speed of propagation C of a capillary (very small) wave in deep water is known to be a function

only of density



, wavelength



, and surface tension Y. Find the proper functional relationship,

completing it with a dimensionless constant. For a given density and wavelength, how does the

propagation speed change if the surface tension is doubled?

Solution 5.13

The “function” of







 and Y must have velocity units. Thus

Problem 5.14

Flow in a pipe is often measured with an orifice plate, as in Fig, P5.14. The volume flow Q is a

function of the pressure drop Δp across the plate, the fluid density ρ, the pipe diameter D, and the

orifice diameter d. Rewrite this functional relationship in dimensionless form

.

Solution 5.14

Write out the dimensions of the variables:

Q p D d





Problem 5.15

The wall shear stress



w in a boundary layer is assumed to be a function of stream velocity U,

boundary layer thickness



, local turbulence velocity u, density



, and local pressure gradient

dp/dx. Using (



, U,



) as repeating variables, rewrite this relationship as a dimensionless function.

Solution 5.15

The relevant dimensions are {



w} = {ML–1T–2}, {U} = {LT–1}, {



} = {L}, {u} = {LT–1},

{



} = {ML–3}, and {dp/dx} = {ML–2T–2}. With n = 6 and j = 3, we expect n − j = k = 3 pi

Problem 5.16

Convection heat-transfer data are often reported as a heat-transfer coefficient h, defined by

Q h A T

=

where

Q

= heat flow, J/s

A = surface area, m2

T = temperature difference, K

The dimensionless form of h, called the Stanton number, is a combination of h, fluid density



, specific

heat cp, and flow velocity V. Derive the Stanton number if it is proportional to h. What are the units

of h?

Solution 5.16

22

33

ML M

If {Q} {hA T}, then {h}{L }{ }, or: {h}

TT

 

=  =  =

   





Problem 5.17

If you disturb a tank of length L and water depth h, the surface will oscillate back and forth at

frequency , assumed here to depend also upon water density



and the acceleration of gravity

g. (a) Rewrite this as a dimensionless function. (b) If a tank of water sloshes at 2.0 Hz on earth,

how fast would it oscillate on Mars (g  3.7 m/s2)?

Solution 5.17

Write out the dimensions of the five variables. We hardly even need Table 5.1:

Problem 5.18

Under laminar conditions, the volume flow Q through a small triangular-section pore of side length

b and length L is a function of viscosity



, pressure drop per unit length p/L, and b. Using the pi

theorem, rewrite this relation in dimensionless form. How does the volume flow change if the pore

size b is doubled?

Solution 5.18

Establish the variables and their dimensions:

Q = fcn(p/L ,



, b )

{L3/T} {M/L2T2} {M/LT} {L}

Problem 5.19

The period of oscillation T of a water surface wave is assumed to be a function of density



,

wavelength



, depth h, gravity g, and surface tension Y. Rewrite this relationship in dimensionless

form. What results if Y is negligible?

Solution 5.19

Establish the variables and their dimensions:

Problem 5.20

A fixed cylinder of diameter D and length L, immersed in a stream flowing normal to its axis at

velocity U, will experience zero average lift. However, if the cylinder is rotating at angular

velocity , a lift force F will arise. The fluid density



is important, but viscosity is secondary

and can be neglected. Formulate this lift behavior as a dimensionless function.

Solution 5.20

No suggestion was given for the repeating variables, but for this type of problem (force

coefficient, lift coefficient), we normally choose (



, U, D) for the task. List the dimensions:

D L U F



