Problem 4.20
A two-dimensional incompressible velocity field has u = K(1 – e–ay), for x L and 0 y .
What is the most general form of v(x, y) for which continuity is satisfied and v = vo at y = 0? What
are the proper dimensions for constants K and a?
Solution 4.20
We can find the appropriate velocity v from two-dimensional continuity:
Problem 4.21
Air flows under steady, approximately one-dimensional conditions through the conical nozzle in
Fig. P4.21. If the speed of sound is approximately 340 m/s, what is the minimum nozzle-diameter
ratio De/Do for which we can safely neglect compressibility effects if Vo = (a) 10 m/s and (b) 30 m/s?
Solution 4.21
If we apply one-dimensional continuity to this duct,
Problem 4.22
In an axisymmetric flow, nothing varies with
and the only nonzero velocities are vr and vz (see
Fig. 4.2). If the flow is steady and incompressible and vz = Bz, where B is constant, find the
most general form of vr which satisfies continuity.
Fig. 4.2 Definition sketch for the
cylindrical coordinate system.
Solution 4.22
With no
variation and no v, the equation of continuity (4.9) becomes
Problem 4.23
A tank volume contains gas at conditions (
o, po, To). At time t = 0 it is punctured by a small
hole of area A. According to the theory of Chap. 9, the mass flow out of such a hole is
approximately proportional to A and to the tank pressure. If the tank temperature is assumed
constant and the gas is ideal, find an expression for the variation of density within the tank.
Solution 4.23
Problem 4.24
For laminar flow between parallel plates (see Fig. 4.12b), the flow is two-dimensional (v 0) if
the walls are porous. A special case solution is
22
( )( )u A Bx h y= − −
, where A and B are
constants. (a) Find a general formula for velocity v if v = 0 at y = 0. (b) What is the value of the
constant B if v = vw at y = +h?
Solution 4.24
(a) Use the equation of continuity to find the velocity v:
Problem 4.25
An incompressible flow in polar coordinates is given by
2
v cos 1
r
b
Kr
=−
2
v sin 1 b
Kr
= − +
Does this field satisfy continuity? For consistency, what should the dimensions of constants K
and b be? Sketch the surface where vr = 0 and interpret.
Solution 4.25
Substitute into plane polar coordinate continuity:
Problem 4.26*
Curvilinear, or streamline, coordinates are defined in Fig. P4.26, where n is normal to the
streamline in the plane of the radius of curvature R. Show that Euler’s frictionless momentum
equation (4.36) in streamline coordinates becomes
/ ( / ) (1/ )( / ) s
V t V V s p s g
+ = − +
(1)
21
n
Vp
Vg
t R n
− − = − +
(2)
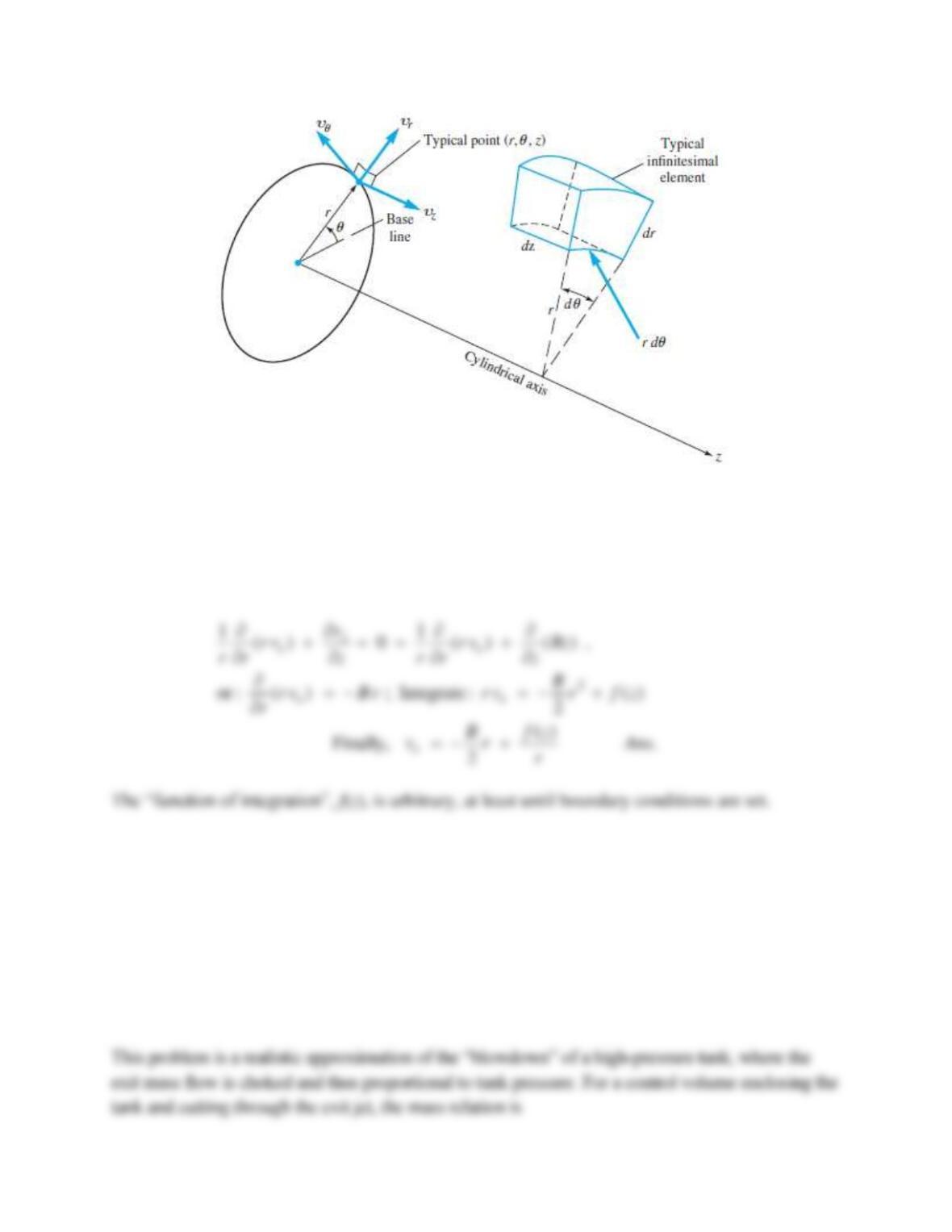
Further show that the integral of Eq. (1) with respect to s is none other than our old friend
Bernoulli’s equation (3.76).
Solution 4.26
This is a laborious derivation, really, the problem is only meant to acquaint the student with
streamline coordinates. The second part is not too hard, though. Multiply the streamwise
Problem 4.27
A frictionless, incompressible steady-flow field is given by
V = 2xyi – y2j
in arbitrary units. Let the density be
o = constant and neglect gravity. Find an expression for the
pressure gradient in the x direction.
Solution 4.27
For this (gravity-free) velocity, the momentum equation is
2
o
u v p, or: [(2xy)(2y ) ( y )(2x 2y )] p
xy
+ = − + − − = −
VV i i j
23
o
Solve for p (2xy 2y ), or: .Ans
= − + 2
o
p
i j 2xy
x
= −
Problem 4.28
For the velocity distribution of Prob. 4.10, (a) check continuity. (b) Are the Navier-Stokes
equations valid? (c) If so, determine p(x,y) if the pressure at the origin is po.
Solution 4.28
Recall u = 4y and v = 2x. It is pretty clear that plane-flow continuity is satisfied:
Problem 4.29
Consider a steady, two-dimensional, incompressible flow of a newtonian fluid in which the
velocity field is known: u = –2xy, v = y2 – x2, and w = 0. (a) Does this flow satisfy conservation
of mass? (b) Find the pressure field p(x, y) if the pressure at point (x = 0, y = 0) is equal to pa.
Solution 4.29
Evaluate and check the incompressible continuity equation:
0 2 2 0 0 (a)
u v w y y Ans.
x y z
+ + = = − + + Yes!
(b) Find the pressure gradients from the Navier-Stokes x– and y-relations:
222
2 2 2 ,:
u u u p u u u
u v w or
x y z x x y z
+ + = − + + +
2 2 2 3
[ 2 ( 2 ) ( )( 2 )] (0 0 0), : 2 ( )
pp
xy y y x x or xy x
xx
− − + − − = − + + + = − +
and, similarly for the y-momentum relation,
2 2 2
2 2 2 ,:
v v v p v v v
u v w or
x y z y x y z
+ + = − + + +
2 2 2 3
[ 2 ( 2 ) ( )(2 )] ( 2 2 0), : = 2 ( )
pp
xy x y x y or x y y
yy
− − + − = − + − + + − +
The two gradients
p/
x and
p/
y may be integrated to find p(x, y):
2 2 4
2 ( ), :
24
y Const
p x y x
p dx f y then differentiate
x
=
= = − + +
2 2 3 3 4
2 ( ) 2 ( ), 2 , : ( ) 2
p df df
x y x y y whence y or f y y C
y dy dy
= − + = − + = − = − +
Finally, the pressure field for this flow is given by
(b)Ans.
2 2 4 4
a
p p (2x y x y )
=−++
`
Problem 4.30
For the velocity distribution of Problem 4.4, determine if (a) the equation of continuity and
(b) the Navier-Stokes equation are satisfied. (c) If the latter is true, find the pressure distribution
p(x,y) when the pressure at the origin equals po.
Solution 4.30
Recall that we were given u = Uo(1+x/L) and v = -Uo y/L. (a) Test continuity:
2 2 4 4
: (2 ) ( , ) (0,0), :
2a
Thus p x y x y C p at x y or
= − + + + = = a
C = p
Problem 4.31
According to potential theory (Chap. 8) for the flow approaching a rounded two-dimensional body,
as in Fig. P4.31, the velocity approaching the stagnation point is given by u = U(1 – a2/x2),
where a is the nose radius and U is the velocity far upstream. Compute the value and position of
the maximum viscous normal stress along this streamline. Is this also the position
of maximum fluid deceleration? Evaluate the maximum viscous normal stress if the fluid is
SAE 30 oil at 20°C, with U = 2 m/s and a = 6 cm.
Problem 4.32
The answer to Prob. 4.14 is
= f(r) only. Do not reveal this to your friends if they are still
working on Prob. 4.14. Show that this flow field is an exact solution to the Navier-Stokes
equations (4.38) for only two special cases of the function f(r). Neglect gravity. Interpret these
two cases physically.
Solution 4.32
Given v
= f(r) and vr = vz = 0, we need only satisfy the
-momentum relation:
Problem 4.33
Consider incompressible flow at a volume rate Q toward a drain at the vertex of a 45 wedge of
width b, as in Fig. P4.33. Neglect gravity and friction and assume purely radial inflow. (a) Find
an expression for vr(r). (b) Show that the viscous term in the r-momentum equation is zero.
(c) Find the pressure distribution p(r) if p = po at r = R.
Solution 4.33
(a) Assume one-dimensional, steady, radial inflow. Then, at any radius r,
Problem 4.34
A proposed three-dimensional incompressible flow field has the following vector form:
V = Kxi + Kyj – 2Kzk
(a) Determine if this field is a valid solution to continuity and Navier-Stokes. (b) If g = –gk, find the
pressure field p(x, y, z). (c) Is the flow irrotational?
Solution 4.34
(a) Substitute this field into the three-dimensional incompressible continuity equation:
Problem 4.35
From the Navier-Stokes equations for incompressible flow in polar coordinates (App. D for
cylindrical coordinates), find the most general case of purely circulating motion
(r),
r =
z = 0, for flow with no slip between two fixed concentric cylinders, as in Fig. P4.35.
Appendix D:
Appendix D continued on next page:
Solution 4.35
The preliminary work for this problem is identical to Prob. 4.32 on an earlier page. That is,
Problem 4.36
A constant-thickness film of viscous liquid flows in laminar motion down a plate inclined at
angle
, as in Fig. P4.36. The velocity profile is
u = Cy(2h – y) v = w = 0
Find the constant C in terms of the specific weight and viscosity and the angle
. Find the
volume flux Q per unit width in terms of these parameters.
Solution 4.36
There is atmospheric pressure all along the surface at y = h, hence
p/
x = 0. The x-momentum
equation can easily be evaluated from the known velocity profile:
Problem 4.37
A viscous liquid of constant ρ and μ falls due to gravity between two plates a distance 2h apart,
as in Fig. P4.37. The flow is fully developed, with a single velocity w = w(x). There are no
applied pressure gradients, only gravity. Solve the Navier-Stokes equation for the velocity profile
between the plates.
Solution 4.37
Only the z–component of Navier-Stokes is relevant:
Problem 4.38
Show that the incompressible flow distribution, in cylindrical coordinates,
where C is a constant, (a) satisfies the Navier-Stokes equation for only two values of n. Neglect
gravity. (b) Knowing that p = p(r) only, find the pressure distribution for each case, assuming
that the pressure at r = R is po. What might these two cases represent?
Solution 4.38
(a) The important direction here is the
-momentum equation, Eq. (D.6):
00 === z
n
rvrCvv
Problem 4.39
Reconsider the angular-momentum balance of Fig. 4.5 by adding a concentrated body couple Cz
about the z axis [6]. Determine a relation between the body couple and shear stress for equilibrium.
What are the proper dimensions for Cz? (Body couples are important in continuous media with
microstructure, such as granular materials.)
Solution 4.39
rR
The couple Cz has to be per unit volume to make physical sense in Eq. (4.39):
Problem 4.40
For pressure-driven laminar flow between parallel plates (see Fig. 4.12b), the velocity
components are u = U(1– y2/ h2), v = 0, and w = 0, where U is the centerline velocity. In the
spirit of Ex. 4.6, find the temperature distribution T(y) for a constant wall temperature Tw.
Solution 4.40
There are no variations with x or z, so the energy equation (4.53) reduces to
Problem 4.41
As mentioned in Sec. 4.10, the velocity profile for laminar flow between two plates, as in
Fig. P4.41, is
max
2
4 ( ) 0
u y h y
uw
h
−
= = =
If the wall temperature is Tw at both walls, use
the incompressible-flow energy equation (4.75) to solve for the temperature distribution T(y)
between the walls for steady flow.
Solution 4.41
Assume T = T(y) and use the energy equation with the known u(y):