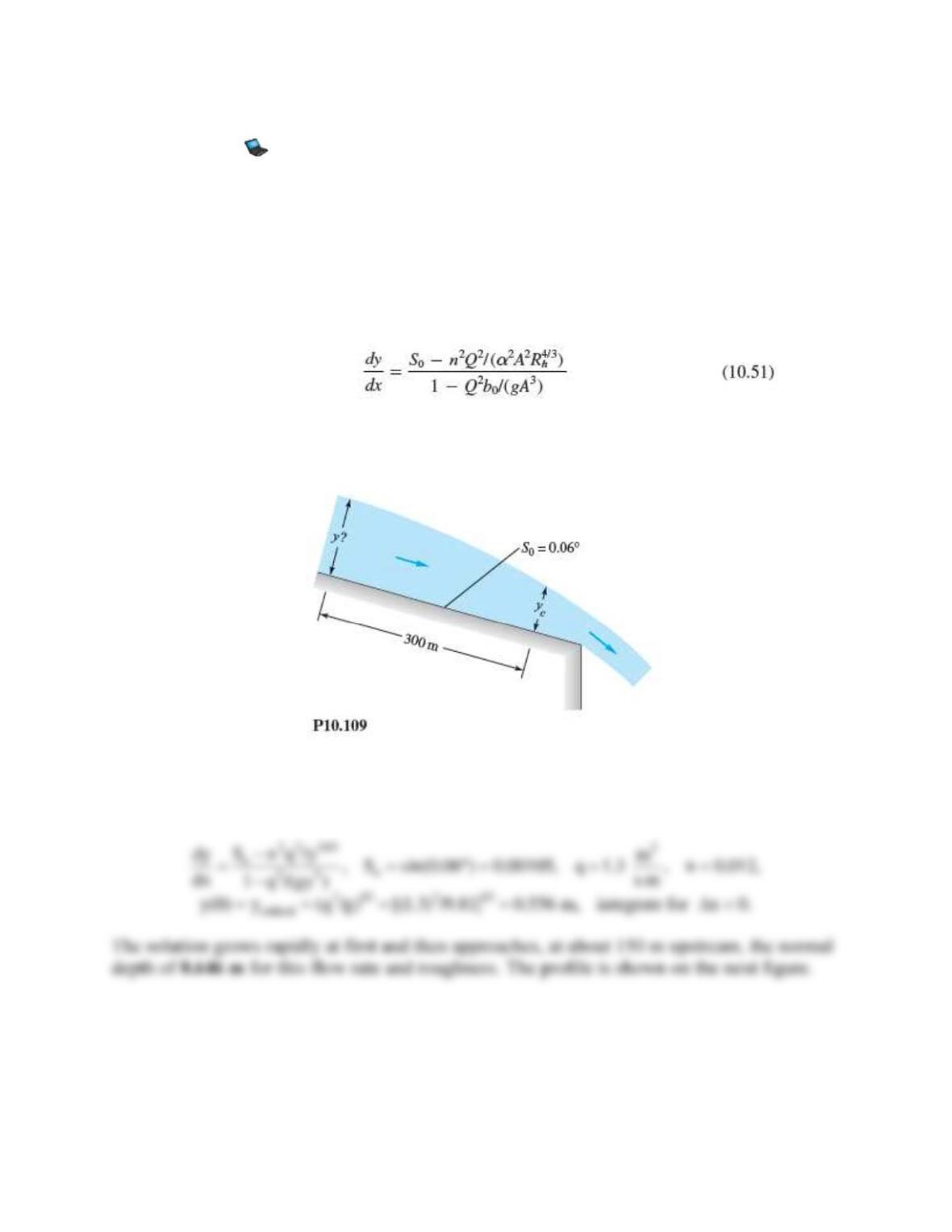
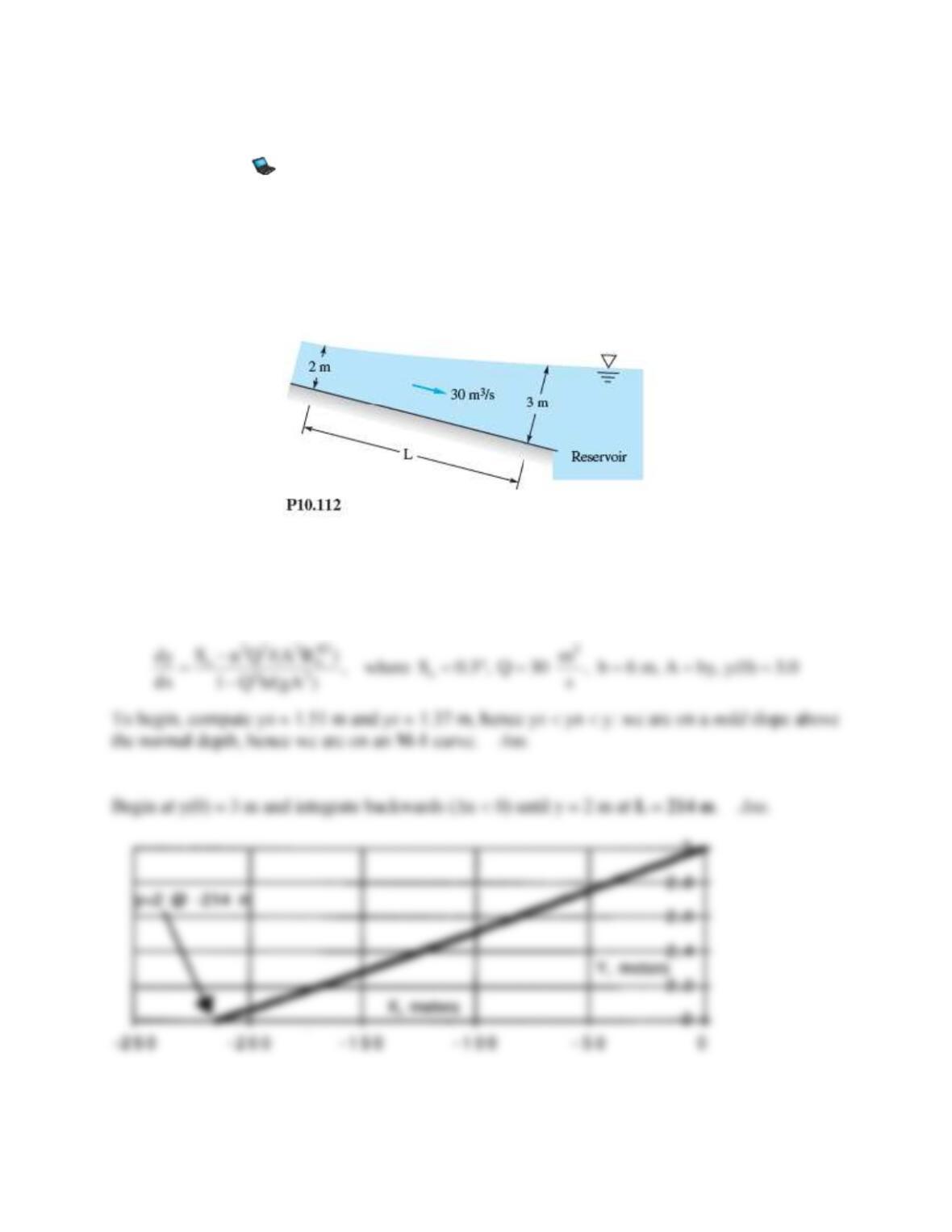
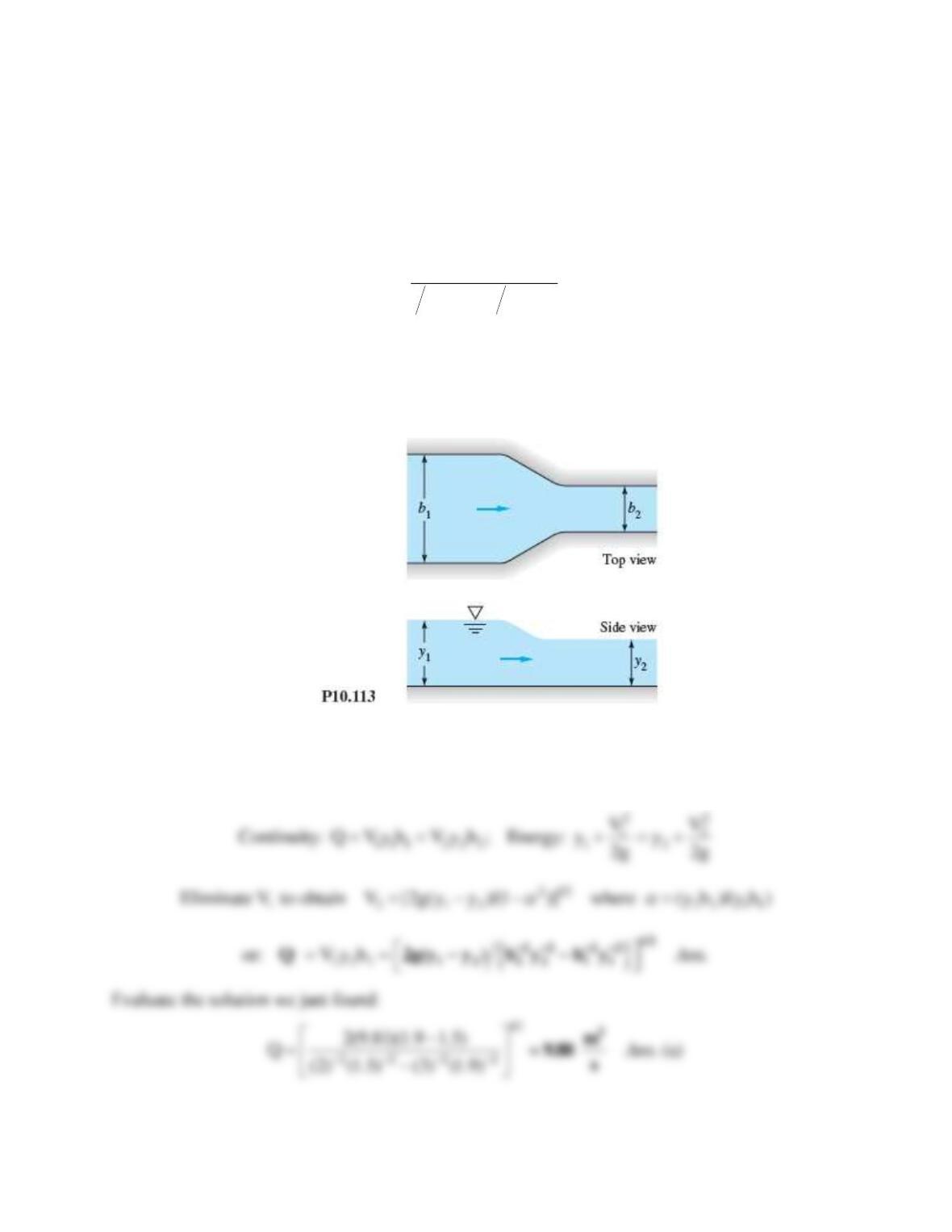
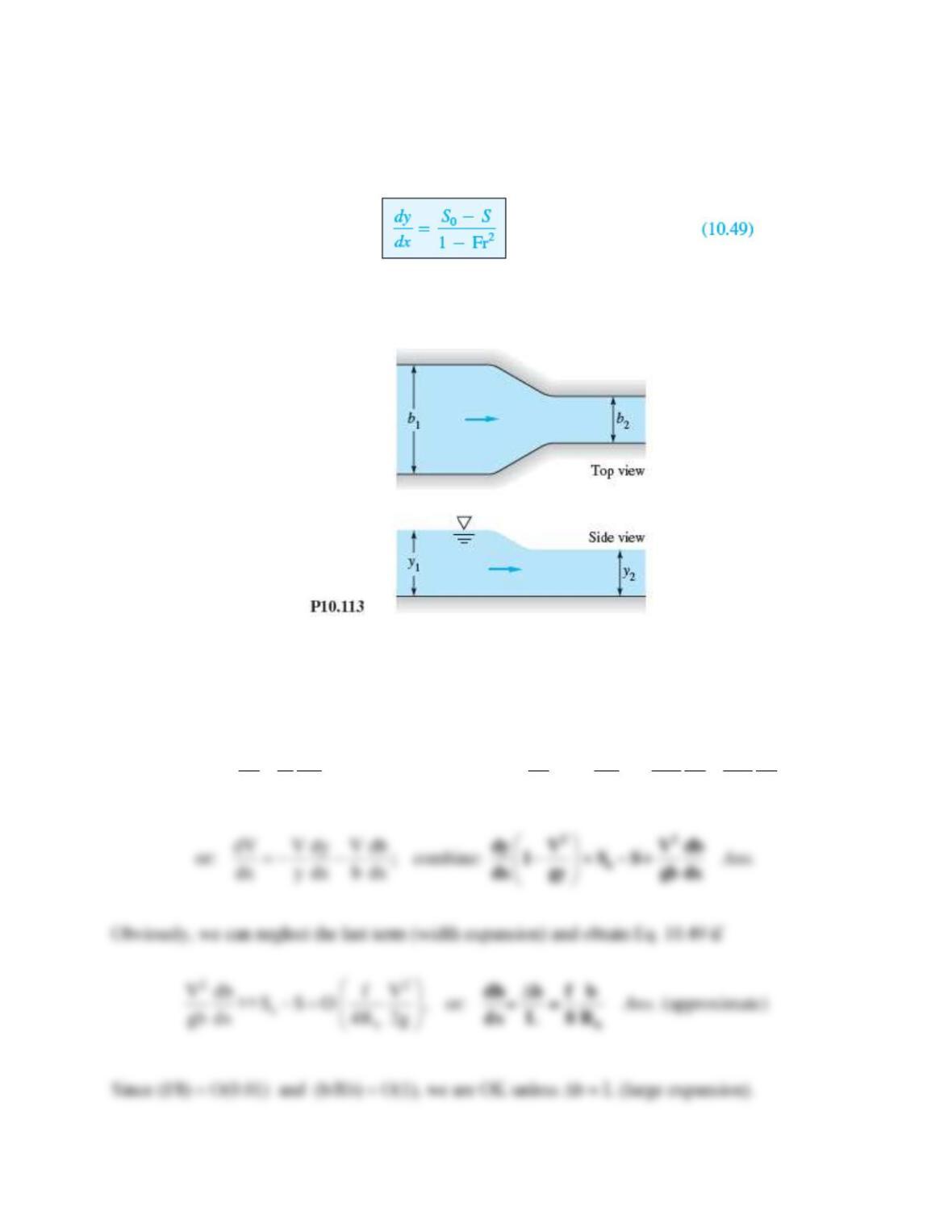
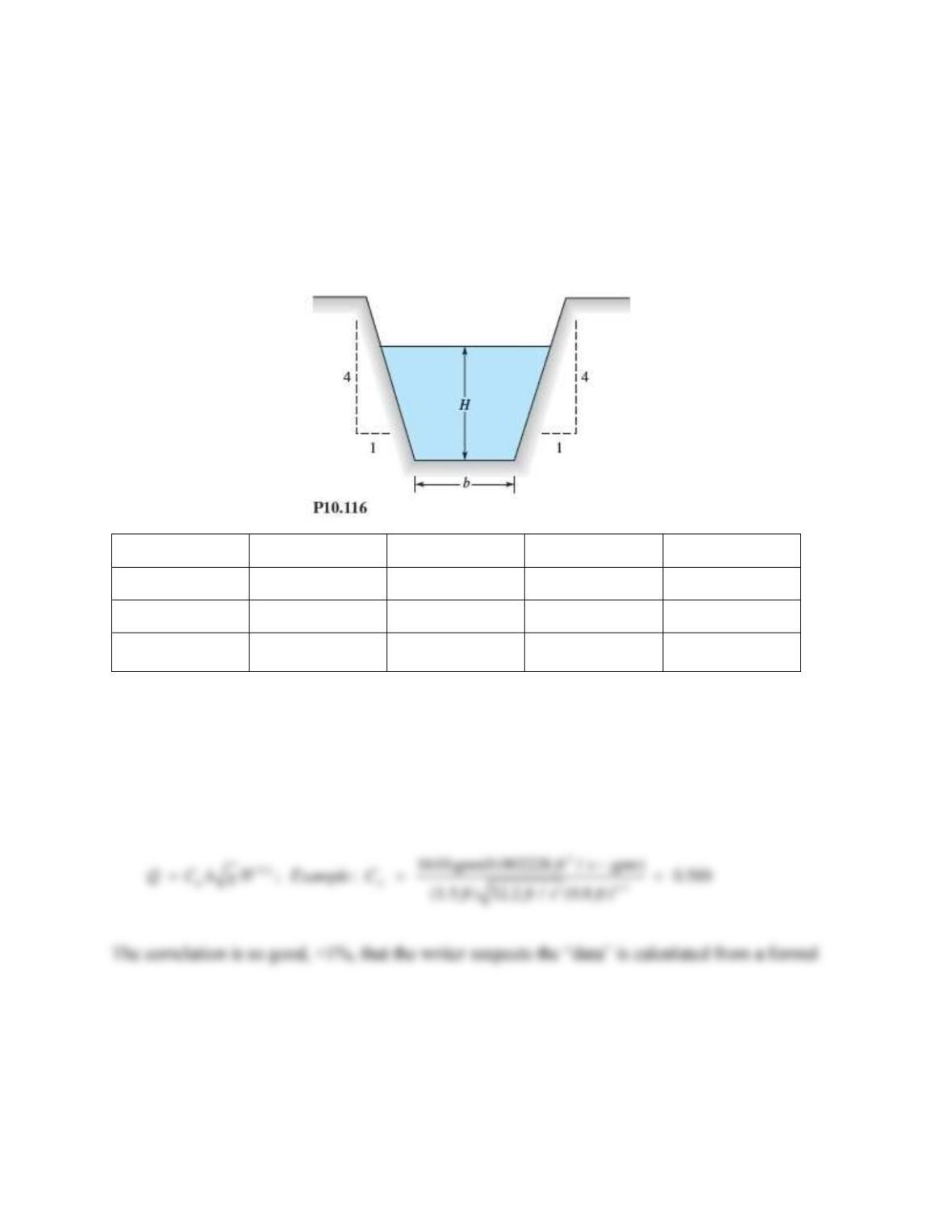
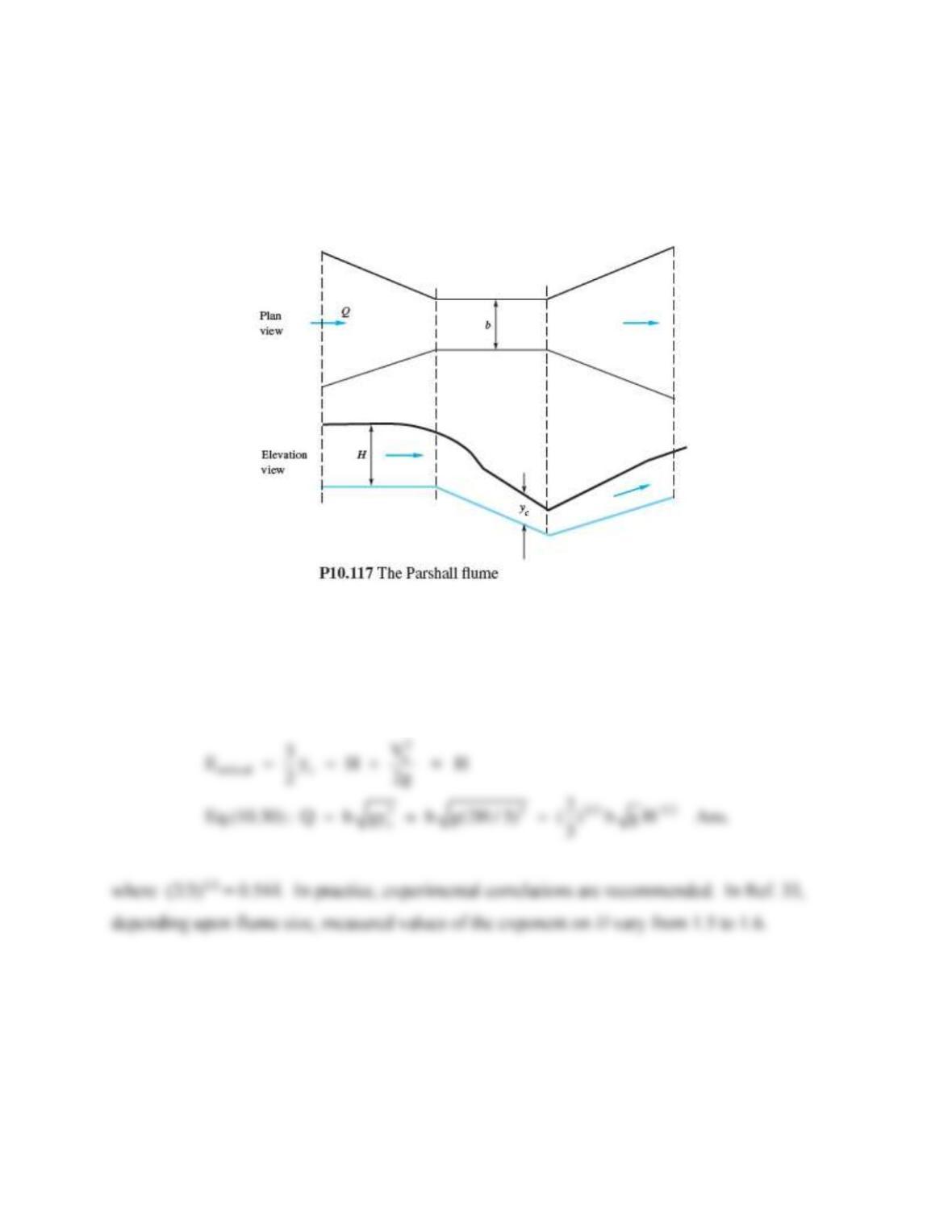
Problem 10.106
A rectangular channel with n = 0.018 and a constant slope of 0.0025 increases its width linearly from b
to 2b over a distance L, as in Fig. P10.106. (a) Determine the variation y(x) along the channel if
b = 4 m, L = 250 m, the initial depth is y(0) = 1.05 m, and the flow rate is 7 m3/s. (b) Then, if your
computer program is running well, determine the initial depth y(0) for which the exit flow will be
exactly critical.
Solution 10.106
We are to solve the gradually-varied-flow relation, Eq. 10.51:
Problem 10.107
A clean-earth wide-channel flow is flowing up an adverse slope with So = −0.002. If the flow rate is
q = 4.5 m3/(s·m), use gradually varied theory to compute the distance for the depth to drop from
3.0 to 2.0 meters.
Solution 10.107
For clean earth, take n 0.022. The basic differential equation is
Problem 10.108
Water flows at 1.5 m3/s along a straight, riveted-steel 90 V-channel (see Fig. 10.41,
= 45).
At section 1, the water depth is 1.0 m. (a) As we proceed downstream, will the water depth rise
or fall? Explain. (b) Depending upon your answer to part (a), calculate, in one numerical
swoop, from gradually varied theory, the distance downstream for which the depth rises (or falls)
0.1 m.
Solution 10.108
For riveted steel, from Table 10.1, n = 0.015. Calculate yn and yc at section 1:
Problem 10.109
Figure P10.109 illustrates a free overfall or dropdown flow pattern, where a channel flow
accelerates down a slope and falls freely over an abrupt edge. As shown, the flow reaches critical
just before the overfall. Between yc and the edge the flow is rapidly varied and does not satisfy
gradually varied theory. Suppose that the flow rate is q = 1.3 m3/(s·m) and the surface is
unfinished cement. Use Eq. (10.51) to estimate the water depth 300 m upstream as shown.
Solution 10.109
For unfinished cement, take n 0.012. The basic differential equation is
Problem 10.110
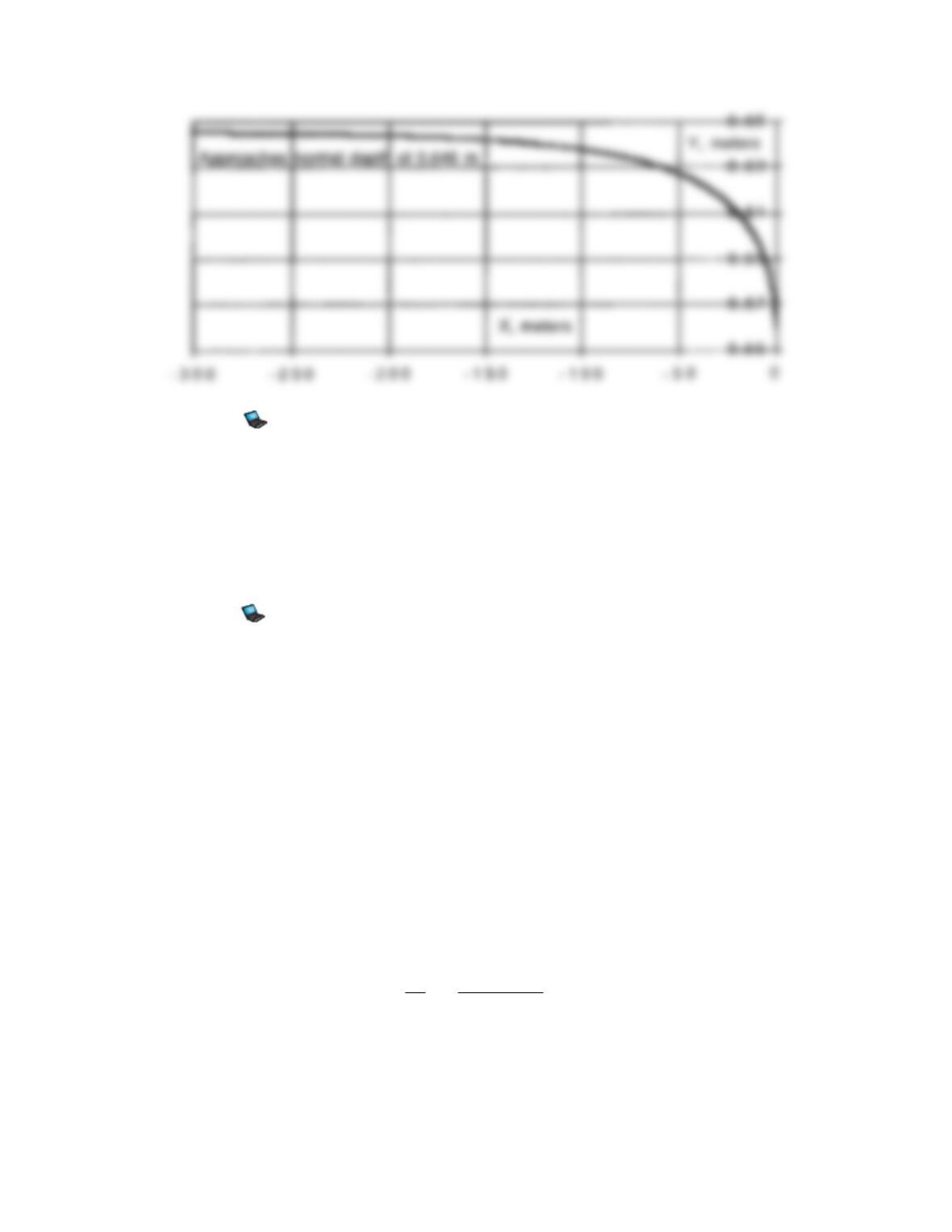
We assumed frictionless flow in solving the bump case, Prob. 10.65, for which V2 = 1.21 m/s and
y2 = 0.826 m over the crest when hmax = 15 cm, V1 = 1 m/s, and y1 = 1 m. However, if the bump
is long and rough, friction may be important. Repeat Prob. 10.65 for the same bump shape,
h = 0.5hmax[1 – cos(2
x/L)], to compute conditions (a) at the crest and (b) at the end of the
bump, x = L. Let hmax = 15 cm and L = 100 m, and assume a clean-earth surface.
Problem 10.65
Program and solve the differential equation of “frictionless flow over a bump,” from Prob. 10.62,
for entrance conditions Vo = 1 m/s and yo = 1 m. Let the bump have the convenient shape
h = 0.5hmax[1 − cos(2
x/L)], which simulates Fig. P10.62. Let L = 3 m, and generate a
numerical solution for y(x) in the bump region 0 x L. If you have time for only one case, use
hmax = 15 cm (Prob. 10.63), for which the maximum Froude number is 0.425. If more time is
available, it is instructive to examine a complete family of surface profiles for hmax 1 cm up to
35 cm (which is the solution of Prob. 10.64).
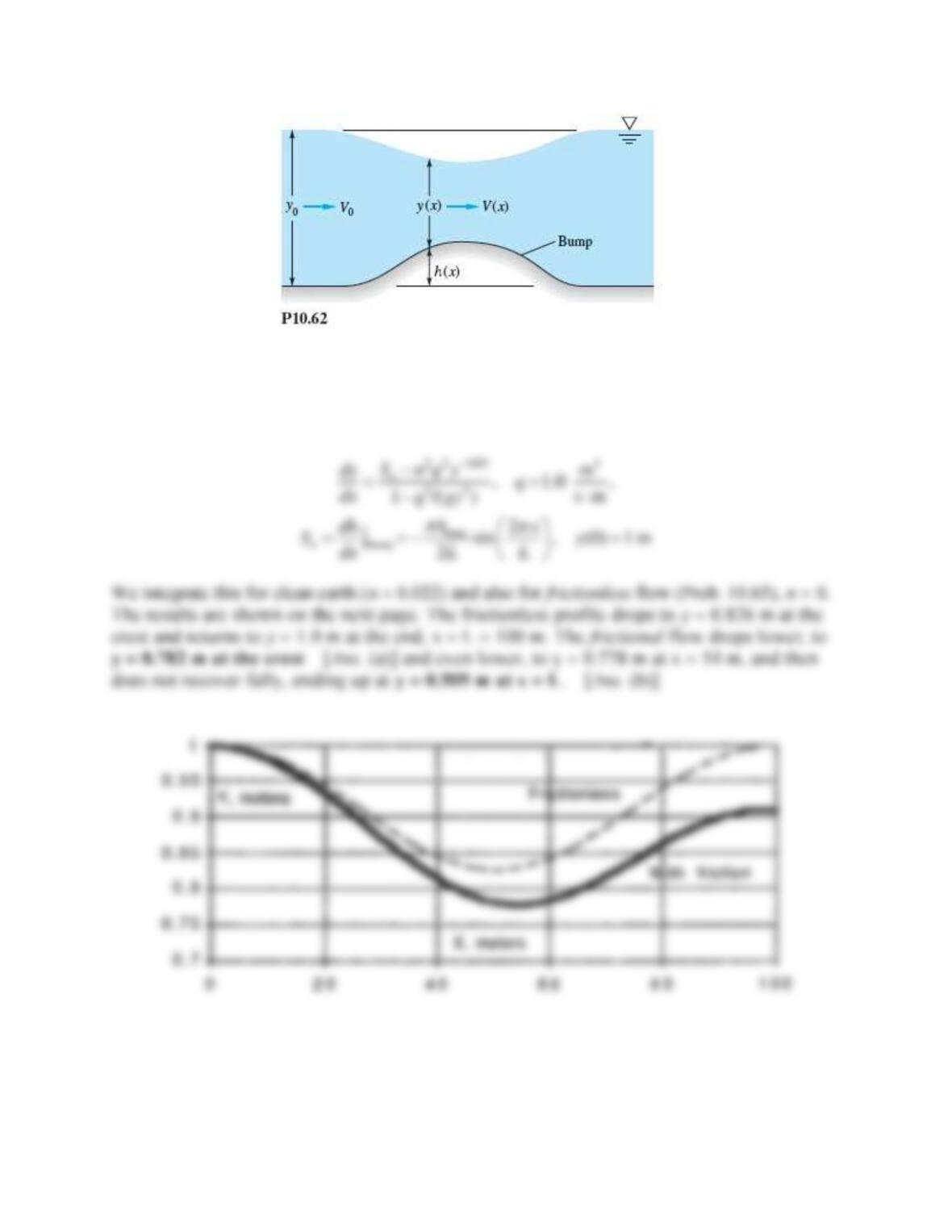
Problem 10.62
Consider the flow in a wide channel over a bump, as in Fig. P10.62. One can estimate the water-
depth change or transition with frictionless flow. Use continuity and the Bernoulli equation to
show that
2
/
1 / ( )
dy dh dx
dx V gy
=− −
Is the drawdown of the water surface realistic in Fig. P10.62? Explain under what conditions the
surface might rise above its upstream position yo.
Solution 10.110
For clean earth, take n = 0.022. The basic differential equation is
Problem 10.111*
The Rolling Dam on the Blackstone River has a weedy bottom and an average flow rate of
900 ft3/s. Assume the river upstream is 150 ft wide and slopes at 10 ft per statute mile. The water
depth just upstream of the dam is 7.7 ft. Calculate the water depth one mile upstream (a) for the
given initial depth, 7.7 ft; and (b) if flashboards on the dam raise this depth to 10.7 ft.
Solution 10.111*
For a weedy bottom, take n ≈ 0.030. Calculate the normal and critical depths:
Problem 10.112
The clean-earth channel in Fig. P10.112 is 6 m wide and slopes at 0.3. Water flows at 30 m3/s
in the channel and enters a reservoir so that the channel depth is 3 m just before the entry.
Assuming gradually varied flow, how far is the distance L to a point in the channel where
y = 2m? What type of curve is the water surface?
Solution 10.112
For clean earth, take n 0.022. The differential equation is Eq. 10.51:
Problem 10.113
Figure P10.113 shows a channel contraction section often called a venturi flume [23, p. 167],
because measurements of y1 and y2 can be used to meter the flow rate. Show that if losses are
neglected and the flow is one–dimensional and subcritical, the flow rate is given by
( ) ( )
1/2
12
2 2 2 2
2 2 1 1
2 ( )
11
g y y
Q
b y b y
−
=
−
Apply this to the special case b1 = 3 m, b2 = 2 m, and y1 = 1.9 m. Find the flow rate (a) if
y2 = 1.5 m. (b) Also find the depth y2 for which the flow becomes critical in the throat.
Solution 10.113
Given the water depths, continuity and energy allow us to eliminate one velocity:
Problem 10.114
For the gate/jump/weir system sketched earlier in Fig. P10.76, the flow rate was determined to be
379 ft3/s. Determine the water depth y4 just upstream of the weir.
Solution 10.114
With the flow rate and weir width known, we can go directly to Eqs. (10.55, 56)
Problem 10.115
Gradually varied theory, Eq. (10.49), neglects the effect of width changes, db/dx, assuming that
they are small. But they are not small for a short, sharp contraction such as the venturi flume in
Fig. P10.113. Show that, for a rectangular section with b = b(x), Eq. (10.49) should be modified
as follows:
2
o
2
[ /( )]( / )
1 Fr
S S V gb db dx
dy
dx
−+
−
Investigate a criterion for reducing this relation to Eq. (10.49).
Solution 10.115
We use the same energy equation, 10.47, but modify continuity, 10.47:
o22
dy V dV Q dV Q dy Q db
Energy: S S; continuity: V ,
dx g dx by dx dx dx
by yb
+ = − = = − −
Problem 10.116
A Cipolletti weir, popular in irrigation systems, is trapezoidal, with sides sloped at 1:4 horizontal
to vertical, as in Fig. P10.116. The following are flow-rate values, from the U. S. Dept. of
Agriculture, for a few different system parameters:
H, ft
0.8
1.0
1.35
1.5
b, ft
1.5
2.0
2.5
3.5
Q, gal/min
1610
3030
5920
9750
Cd (calculated)
0.589
0.595
0.593
0.595
Use this data to correlate a Cipolletti weir formula with a reasonably constant weir coefficient.
Solution 10.116
We have done this, and added a bottom row to the table. The correlation is
Problem 10.117
A popular flow-measurement device in agriculture is the Parshall flume [33], Fig. P10.117,
named after its inventor, Ralph L. Parshall, who developed it in 1922 for the U. S. Bureau of
Reclamation. The subcritical approach flow is driven, by a steep constriction, to go critical
(y = yc) and then supercritical. It gives a constant reading H for a wide range of tailwaters.
Derive a formula for estimating Q from measurement of H and knowledge of constriction width
b. Neglect the entrance velocity head.
Solution 10.117
The rectangular constriction fits the specific energy conditions of Eq. (10.31):
Problem 10.118*
Using a Bernoulli-type analysis similar to Fig. 10.16a, show that the theoretical discharge of the
V-shaped weir in Fig. P10.118 is given by
1/2 5/2
0.7542 tanQ g H
=
Solution 10.118
As in Eq. 10.52, assume that velocity V in any strip of height dz and width b, where z is
measured down from the top, is V (2gz) and integrate for the flow rate:
Problem 10.119
Data by A. T. Lenz for water at 20C (reported in Ref. 23) show a significant increase of
discharge coefficient of V-notch weirs (Fig. P10.118) at low heads. For
= 20, some measured
values are as follows:
H, ft:
0.2
0.4
0.6
0.8
1.0
Cd:
0.499
0.470
0.461
0.456
0.452
Determine if these data can be correlated with Reynolds and Weber numbers vis-à-vis Eq.
(10.61). If not, suggest another correlation.
Solution 10.119
There is little or no Reynolds number effect. We can ascribe the entire effect to surface tension
Y, or Weber number We =
gH2/Y.
Problem 10.120
The rectangular channel in Fig. P10.120 contains a V-notch weir as shown. The intent is to meter
flow rates between 2.0 and 6.0 m3/s with an upstream hook gage set to measure water depths
between 2.0 and 2.75 m. What are the most appropriate values for the notch height Y and the
notch half-angle
Solution 10.120
There is an exact solution to this problem which uses the full range of water depth to measure the
full range of flow rates. Of course, there are also a wide variety of combinations of (
, Y) which