Problem 10.41
Determine the most efficient value of
for the V-shaped channel of Fig. P10.41.
Solution 10.41
Given the (simple) geometric properties
Problem 10.42
It is desired to deliver 30,000 gal/min of water in a brickwork channel laid on a slope of 1:100.
Which would require fewer bricks, in uniform flow: (a) a V-channel with
= 45, as in
Fig. P10.41, or (b) an efficient rectangular channel with b = 2y?
Solution 10.42
For brickwork, from Table 10.1, n = 0.015.
The answer may be surprising, but it is hard to
Same perimeter, same number of bricks! These two designs are equally successful.
Problem 10.43
Determine the most efficient dimensions for a clay tile rectangular channel to carry
110,000 gal/min on a slope of 0.002.
Solution 10.43
For clay tile, from Table 10.1, n = 0.014. Convert 110,000 gal/min to 245 ft3/s. The most
Problem 10.44
What are the most efficient dimensions for a half-hexagon cast-iron channel to carry
15000 gal/min of water at a slope of 0.16?
Solution 10.44
For cast iron, take n 0.013. We know from Fig. 10.7 for a half-hexagon that
Problem 10.45
Calculus tells us that the most efficient wall angle for a V-shaped channel (Fig. P10.41) is
= 45. It yields the highest normal flow rate for a given area. But is this a sharp or a flat
maximum? For a flow area of 1 m2 and an unfinished-concrete channel of slope 0.004, plot the
normal flow rate Q, in m3/s, versus angle for the range 30
60 and comment.
Solution 10.45
The area is A = y2cot(
), so, if A = 1 m2,
Fig. P10.45
Problem 10.46
It is suggested that a channel which reduces erosion has a parabolic shape, as in Fig. P10.46.
Formulas for area and perimeter of the parabolic cross-section are as follows [ 7, p. 36]:
()
22
0
4
21
; 1 ln , where
1
32
o
h
b
A bh P b
= = + + =
++
For uniform flow conditions, determine the most efficient ratio ho/b for this channel (minimum
perimeter for a given constant area).
Solution 10.46
We are to minimize P for constant A, and this time, unlike Prob. 10.37, the algebra is too heavy,
Problem 10.47
Calculus tells us that the most efficient water depth for a rectangular channel (such as Fig. E10.1)
is y/b = 1/2. It yields the highest normal flow rate for a given area. But is this a sharp or a flat
maximum? For a flow area of 1 m2 and a clay tile channel with a slope of 0.006, plot the normal
flow rate Q, in m3/s, versus y/b for the range 0.3 y/b 0.7 and comment.
Solution 10.47
The area = 1 m2 = (y)(b), so y/b = A/b2.
y
A = 1 m2
Problem 10.48
A wide, clean-earth river has a flow rate q = 150 ft3/(s·ft). What is the critical depth? If the actual
depth is 12 ft, what is the Froude number of the river? Compute the critical slope by (a)
Manning’s formula and (b) the Moody chart.
Solution 10.48
For clean earth, take n 0.030 and roughness
0.8 ft. The critical depth is
Problem 10.49
Find the critical depth of the brick channel in Prob. 10.34 for both the 4 – and 8-ft widths. Are the
normal flows subcritical or supercritical?
Problem 10.34
A brick rectangular channel with S0 = 0.002 is designed to carry 230 ft3/s of water in uniform
flow. There is an argument over whether the channel width should be 4 or 8 ft. Which design
needs fewer bricks? By what percentage?
Solution 10.49
For brick, take n 0.015. Recall and extend our results from Prob. 10.34:
Problem 10.50
A pencil point piercing the surface of a rectangular channel flow creates a wedge-like 25 half-
angle wave, as in Fig. P10.50. If the channel surface is painted steel and the depth is 35 cm,
determine (a) the Froude number, (b) the critical depth; and (c) the critical slope for uniform
flow.
Solution 10.50
For painted steel, take n 0.014. The wave angle and depth give
Problem 10.51
An unfinished concrete duct, of diameter 1.5 m, is flowing half-full at 8.0 m3/s. (a) Is this a
critical flow? If not, what is (b) the critical flow rate, (c) the critical slope, and (d) the Froude
number? (e) If the flow is uniform, what is the slope of the duct?
Solution 10.51
For unfinished concrete, from Table 10.1, n = 0.014. (b) Compute the critical flow rate:
Problem 10.52
Water flows full in an asphalt half-hexagon channel of bottom width W. The flow rate is 12 m3/s.
Estimate W if the Froude number is exactly 0.60.
Solution 10.52
For asphalt, n = 0.016, but we don’t need n because critical flow is independent of roughness.
Work out the properties of a half-hexagon:
Problem 10.53
For the river flow of Prob. 10.48, find the depth y2 which has the same specific energy as the
given depth y1 = 12 ft. These are called conjugate depths. What is Fr2?
Problem 10.48
A wide, clean-earth river has a flow rate q = 150 ft3/(s·ft). What is the critical depth? If the actual
depth is 12 ft, what is the Froude number of the river? Compute the critical slope by (a)
Manning’s formula and (b) the Moody chart.
Solution 10.53
Recall from Prob. 10.48 that the flow rate is q = 150 ft3/(s·ft). Hence
Problem 10.54
A clay tile V-shaped channel has an included angle of 70 and carries 8.5 m3/s. Compute (a) the
critical depth, (b) the critical velocity, and (c) the critical slope for uniform flow.
Solution 10.54
For clay tile, take n 0.014. The cross-section properties are
Problem 10.55
A trapezoidal channel resembles Fig. 10.7 with b = 1 m and
= 50. The water depth is 2 m and
Q = 32 m3/s. If you stick your fingernail in the surface, as in Fig. P10.50, what half-angle wave
might appear?
Solution 10.55
The cross-section properties are
Problem 10.56
A 4-ft-diameter finished-concrete sewer pipe is half full of water. (a) In the spirit of Fig. 10.4a,
estimate the speed of propagation of a small-amplitude wave propagating along the channel.
(b) If the water is flowing at 14,000 gal/min, calculate the Froude number.
Solution 10.56
For finished concrete, n = 0.012, but we don’t need this number! (a) From the critical-flow
analysis, Eq. (10.37b), the critical velocity is the desired speed of wave propagation:
Problem 10.57
Consider the V-shaped channel of arbitrary angle in Fig. P10.41. If the depth is y, (a) find an
analytic expression for the propagation speed co of a small-disturbance wave along this channel.
[HINT: Eliminate flow rate from the analyses in Sec. 10.4.] If
= 45 and the depth is 1 m,
determine (b) the propagation speed; and (c) the flow rate if the channel is running at a Froude
number of 1/3.
Solution 10.57
The algebra is given in Ex.10.6:
Problem 10.58
For a half-hexagon channel running full, find an analytic expression for the propagation speed of
a small-disturbance wave travelling along this channel. Denote the bottom width as b and use
Fig. 10.7 as a guide.
Solution 10.58
In Fig. 10.7, for a half-hexagon, let W = b. Then y = b sin60º, and the area and top width are
Problem 10.59
Uniform water flow in a wide brick channel of slope 0.02 moves over a 10-cm bump as in
Fig. P10.59. A slight depression in the water surface results. If the minimum water depth over the
bump is 50 cm, compute (a) the velocity over the bump; and (b) the flow rate per meter of width.
Solution 10.59
For brickwork, take n 0.015. Since the water level decreases over the bump, the upstream flow
is subcritical. For a wide channel, Rh = y/2, and Eq. 10.39 holds:
Problem 10.60
Water, flowing in a rectangular channel 2 m wide, encounters a bottom bump 10 cm high. The
approach depth is 60 cm, and the flow rate 4.8 m3/s. Determine (a) the water depth, (b) velocity,
and (c) Froude number above the bump. HINT: The change in water depth is rather slight, only
about 8 cm.
Solution 10.60
First compute the approach velocity and Froude number:
1
11
11
4.8 4.0
4.0 ; 1.65
(2.0)(0.6) 9.81(0.6)
o
V
Qm
V Fr
b y s gy
= = = = = =
Problem 10.61
Modify Prob. 10.59 as follows: Again assuming uniform subcritical approach flow (V1, y1) find
(a) the flow rate q; and (b) the height y2 for which the flow at the crest of the bump is exactly
critical (Fr2 = 1.0).
Problem 10.59
Uniform water flow in a wide brick channel of slope 0.02 moves over a 10-cm bump as in
Fig. P10.59. A slight depression in the water surface results. If the minimum water depth over the
bump is 50 cm, compute (a) the velocity over the bump; and (b) the flow rate per meter of width.
Solution 10.61
The basic analysis above, for uniform upstream flow plus a bump, still holds:
Problem 10.62
Consider the flow in a wide channel over a bump, as in Fig. P10.62. One can estimate the water–
depth change or transition with frictionless flow. Use continuity and the Bernoulli equation to
show that
2
/
1 / ( )
dy dh dx
dx V gy
=− −
Is the drawdown of the water surface realistic in Fig. P10.62? Explain under what conditions the
surface might rise above its upstream position yo.
Solution 10.62
This is a form of frictionless “gradually–varied” flow theory (Sect. 10.6). Use the frictionless
energy equation from upstream to any point along the bump section:
Problem 10.63
Problem 10.62
Consider the flow in a wide channel over a bump, as in Fig. P10.62. One can estimate the water-
depth change or transition with frictionless flow. Use continuity and the Bernoulli equation to
show that
2
/
1 / ( )
dy dh dx
dx V gy
=− −
Is the drawdown of the water surface realistic in Fig. P10.62? Explain under what conditions the
surface might rise above its upstream position yo.
Solution 10.63
Here we don’t need to differentiate, just apply Eq. 10.39 directly:
Problem 10.64
For the rectangular channel in Prob. P10.60, the Froude number over the bump is about 1.37,
which is 17 percent less than the approach value. For the same entrance conditions, find the
bump height
h that causes the bump Froude number to be 1.00.
Problem 10.60
Water, flowing in a rectangular channel 2 m wide, encounters a bottom bump 10 cm high. The
approach depth is 60 cm, and the flow rate 4.8 m3/s. Determine (a) the water depth, (b) velocity,
and (c) Froude number above the bump. HINT: The change in water depth is rather slight, only
about 8 cm.
Solution 10.64
Recall that bo = 2 m, Q = 4.8 m3/s, and y1 = 60 cm. The bump height is the essential unknown in
Eq. (10.39):
Problem 10.65
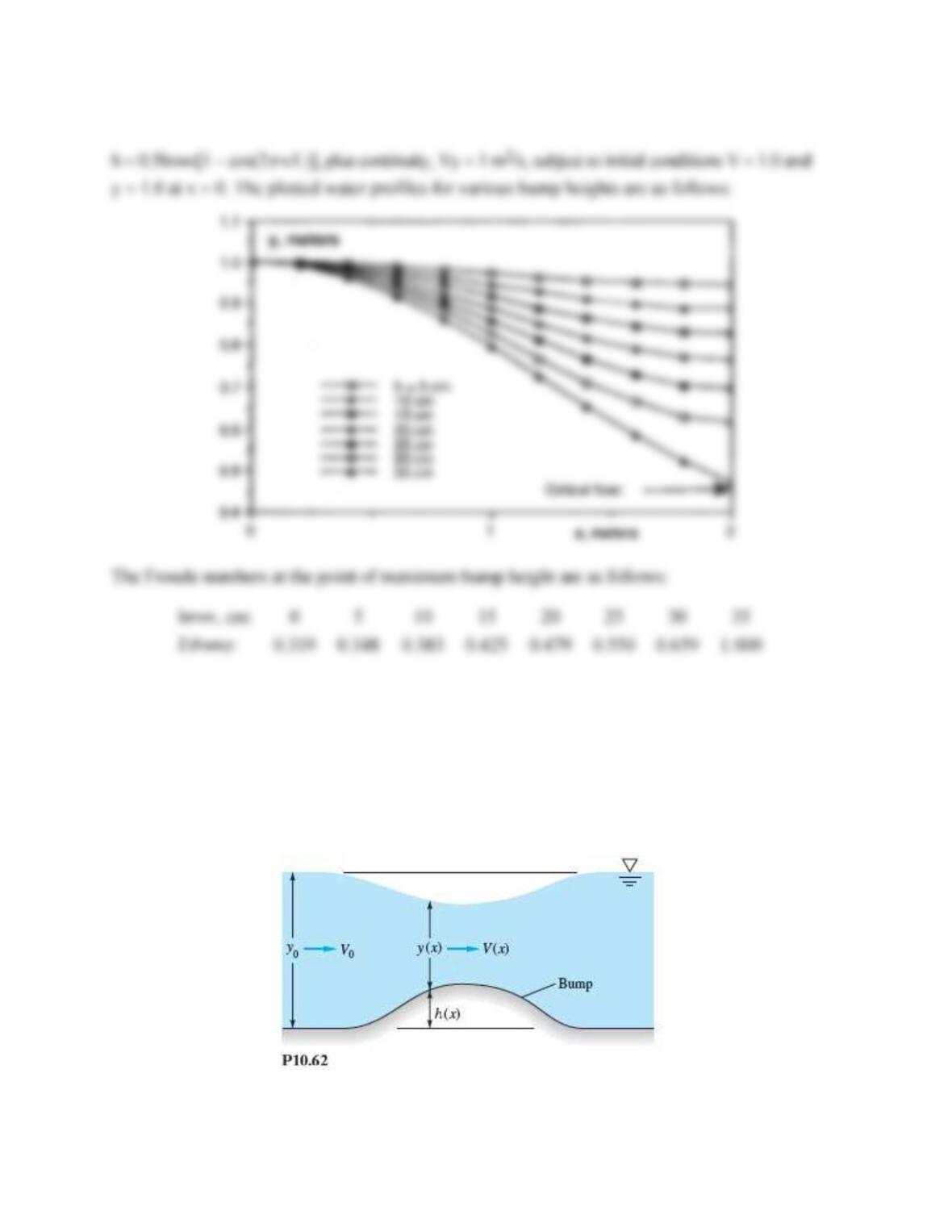
Program and solve the differential equation of “frictionless flow over a bump,” from Prob. 10.62,
for entrance conditions Vo = 1 m/s and yo = 1 m. Let the bump have the convenient shape
h = 0.5hmax[1 − cos(2
x/L)], which simulates Fig. P10.62. Let L = 3 m, and generate a
numerical solution for y(x) in the bump region 0 x L. If you have time for only one case, use
hmax = 15 cm (Prob. 10.63), for which the maximum Froude number is 0.425. If more time is
available, it is instructive to examine a complete family of surface profiles for hmax 1 cm up to
35 cm (which is the solution of Prob. 10.64).
Problem 10.62
Consider the flow in a wide channel over a bump, as in Fig. P10.62. One can estimate the water–
depth change or transition with frictionless flow. Use continuity and the Bernoulli equation to
show that
2
/
1 / ( )
dy dh dx
dx V gy
=− −
Is the drawdown of the water surface realistic in Fig. P10.62? Explain under what conditions the
surface might rise above its upstream position yo.
Problem 10.63
In Fig. P10.62, let Vo = 1 m/s and yo = 1 m. If the maximum bump height is 15 cm, estimate
(a) the Froude number over the top of the bump; and (b) the maximum depression in the water
surface.
Problem 10.64
For the rectangular channel in Prob. P10.60, the Froude number over the bump is about 1.37,
which is 17 percent less than the approach value. For the same entrance conditions, find the
bump height
h that causes the bump Froude number to be 1.00.
Problem 10.60
Water, flowing in a rectangular channel 2 m wide, encounters a bottom bump 10 cm high. The
approach depth is 60 cm, and the flow rate 4.8 m3/s. Determine (a) the water depth, (b) velocity,
and (c) Froude number above the bump. HINT: The change in water depth is rather slight, only
about 8 cm.
Solution 10.65
We solve the differential equation dy/dx = −(dh/dx)/[1 − V2/(gy)], with
Problem 10.66*
In Fig. P10.62 let Vo = 5.5 m/s and yo = 90 cm. (a) Will the water rise or fall over the bump?
(b) For a bump height of 30 cm, determine the Froude number over the bump. (c) Find the bump
height that will cause critical flow over the bump.
Solution 10.66*