Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
61
49.7 m3/sec. The excavated earth channel is a well-maintained (clean) with a flow slope of
0.2% and side slopes of 4:1 (H:V). Solve using successive substitution and Figure 6.4.
5. A grass-lined roadside channel (n = 0.02) is triangular in shape with 30° side slopes and a
bottom slope of 0.006. Determine the normal depth of flow when the discharge is 4 cfs
(ft3/sec). Check your solution using appropriate computer software.
6. Find the best hydraulic (rectangular) channel cut in rock (n = 0.035) to pass 25m3/sec on a
slope of 0.003 m/m. Determine the excavation volume of the 100-m-long channel
7. A 12-ft-wide rectangular channel conveys 3,030 cfs. Determine the normal and critical
depths for the concrete channel (1% slope). Also determine the flow classification (critical,
supercritical, or subcritical) when the channel flows at normal depth.
62
8. A 60-cm-diameter concrete pipe on a 1:400 slope carries water at a depth of 30 cm.
Determine the flow rate and flow classification (subcritical, critical, or supercritical).
9. Water flows in a long, uniform trapezoidal channel lined with brick (n = 0.013) at a depth of
4.5 feet. The base width of the channel is 16.0 ft., the side slopes are 3:1 (H:V), and the
bottom drops a foot for every 1000 feet of length. Determine the velocity of flow and the
flow classification (subcritical, critical, or supercritical).
10. A hydraulic jump occurs in a rectangular channel that is 7 m wide. The initial depth is 0.8 m
and the sequent depth if 3.1 m. Determine the energy loss and the discharge in the channel.
Also determine the Froude number before and after the jump.
63
11. A hydraulic jump occurs in 12-ft wide rectangular channel. If the flow rate is 403 cfs and the
downstream depth is 5 feet, determine the upstream depth, the loss of energy in the jump, and
the Froude number before and after the jump.
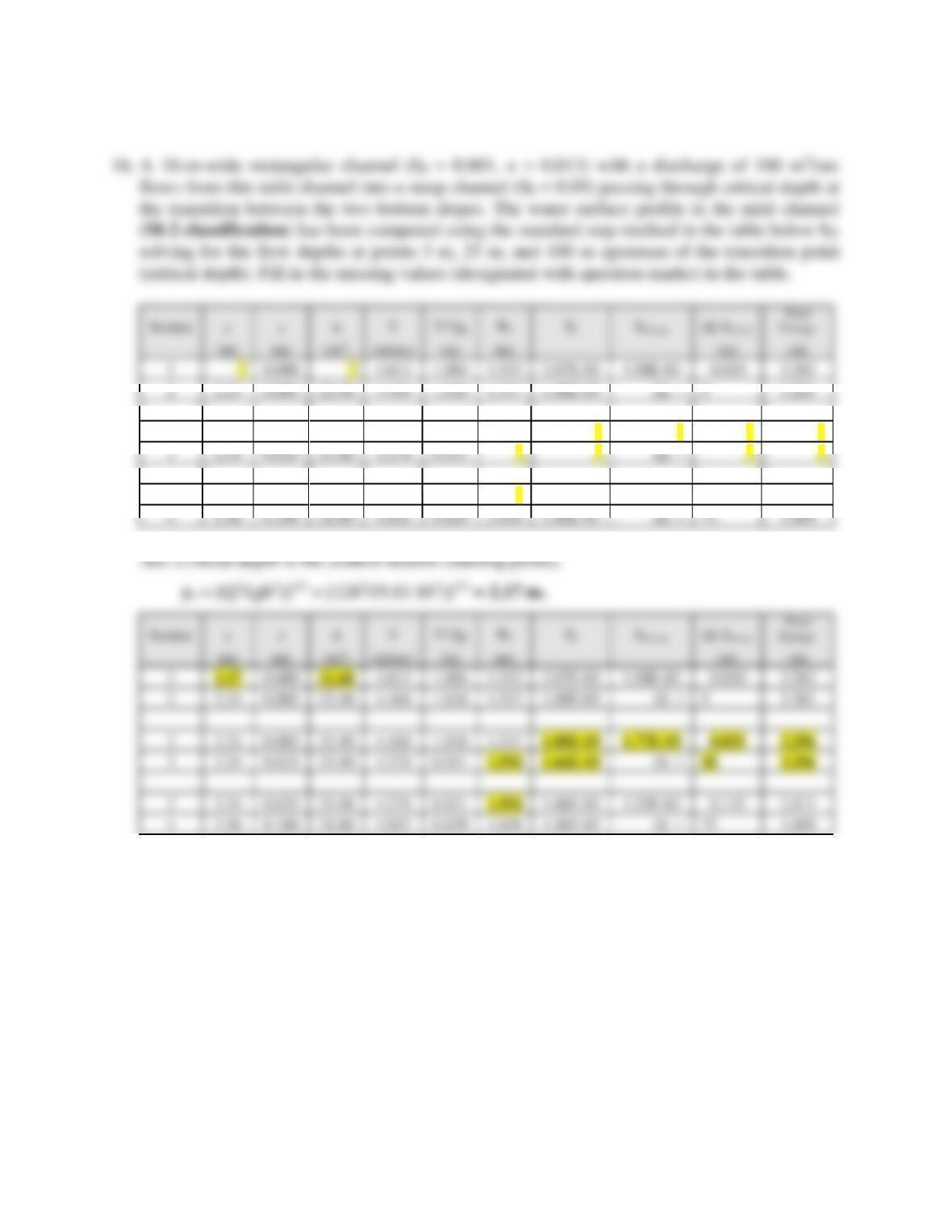
12. Water flows at a rate of 22.8 m3/sec in a trapezoidal channel (n = 0.04) with a bottom width
of 3 m, side slopes of 2:1 (H:V), and a bottom slope of 0.005. At a certain location, the
bottom slope increases to 0.022 with no change in channel dimensions. Normal depths are
1.83 m (upstream) and 1.27 m (downstream). Determine the channel and flow classification
(e.g., M-3, S-2, etc.) just upstream of the break in slope. Explain your supporting logic.
13. Water flows at the rate of 50 m3/sec in a 5-m-wide, rectangular channel (n = 0.011) at a depth
of 1.90 m where the bottom elevation is 150 m above MSL. Upstream 100 m, the depth is
2.00 m where the bottom elevation is 151 m above MSL. What is the slope of the energy
grade line in this section of channel? If critical depth is 2.17 m, determine the channel and
flow classification (e.g., M-3, S-2, etc.). (Note: MSL stands for Mean Sea Level, the datum.)
14. A trapezoidal, concrete channel (n = 0.013) has an 8-ft bottom width and z = 1.0 side slope. It
discharges 650 ft3/sec on a 0.001 channel slope. The channel is flowing at normal depth (5.85
ft) when it encounters an obstruction. The obstruction causes the depth to rise to 7.00 ft. If
critical depth is 4.80 ft, determine the channel and flow classification (e.g., M-3, S-2, etc.).
16. A 10-m-wide rectangular channel (S0 = 0.001, n = 0.013) with a discharge of 100 m3/sec
flows from this mild channel into a steep channel (S0 = 0.05) passing through critical depth at
the transition between the two bottom slopes. The water surface profile in the mild channel
(M-2 classification) has been computed using the standard step method in the table below by
solving for the flow depths at points 5 m, 25 m, and 100 m upstream of the transition point
(critical depth). Fill in the missing values (designated with question marks) in the table.
Section
y
z
A
V
V2/2g
Rh
Se
Se(avg)
ΔL∙Se(avg)
Total
Energy
(m)
(m)
(m2)
(m/sec)
(m)
(m)
(m)
(m)
1
?
0.000
?
4.613
1.084
1.512
2.07E-03
1.98E-03
0.010
3.262
2
2.24
0.005
22.40
4.464
1.016
1.547
1.88E-03
ΔL =
5
3.261
2
2.24
0.005
22.40
4.464
1.016
1.547
?
?
?
?
3
2.34
0.025
23.40
4.274
0.931
?
?
ΔL =
?
?
3
2.34
0.025
23.40
4.274
0.931
?
1.66E-03
1.53E-03
0.115
3.411
4
2.48
0.100
24.80
4.032
0.829
1.658
1.40E-03
ΔL =
75
3.409
