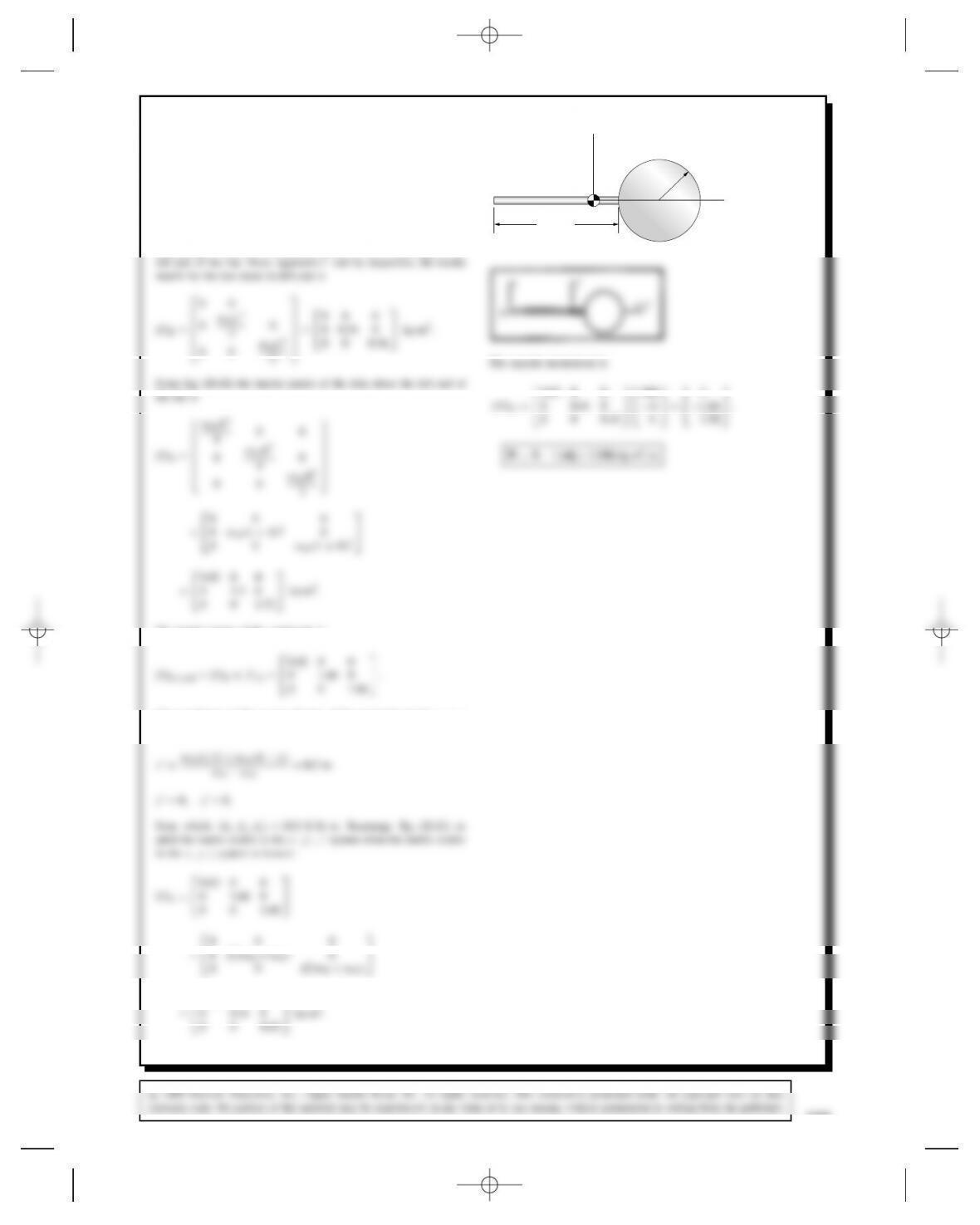
Problem 20.92 A 3-kg slender bar is rigidly attached
to a 2-kg thin circular disk. In terms of the body-fixed
coordinate system shown, the angular velocity of the
composite object is ω=100i−4j+6k(rad/s). What is
the object’s angular momentum about its center of mass?
y
x
600 mm
200 mm
Solution: Choose a coordinate system x,y,zoriginating at the
Problem 20.93* The mass of the homogeneous slen-
der bar is m. If the bar rotates with angular velocity
ω=ω0(24i+12j−6k), what is its angular momentum
about its center of mass?
y
x
z
b
b
b
b
700
Problem 20.94* The 8-kg homogeneous slender bar
has ball-and-socket supports at Aand B.
(a) What is the bar’s moment of inertia about the axis
AB?
(b) If the bar rotates about the axis AB at 4 rad/s, what
is the magnitude of its angular momentum about its
axis of rotation?
y
A
x
B
1 m
4=2.667 kg-m2,
4=10.0 kg-m2
4=8.667 kg-m2,
m
I(RA)
xz =I(RG)
xz +dxdz
4=4.0 kg-m2,
m
4=1.0 kg-m2
Sum the two inertia matrices:
3.333 −2−4
−4−18.667
where the negative signs are a consequence of the definition of the
2=9.333 kg-m2
2=5.333 kg-m2,
I(CA)
xy =I(CG)
xy +dxdy
m
702
Problem 20.95* The 8-kg homogeneous slender bar
in Problem 20.94 is released from rest in the position
shown. (The x–zplane is horizontal.) What is the
magnitude of the bar’s angular acceleration about the
axis AB at the instant of release?
Problem 20.96 In terms of a coordinate system x′y′z′
with its origin at the center of mass, the inertia matrix
of a rigid body is
[I′]=20 10 −10
10 60 0
Ix′z′=10 kg-m2,
From Eq. (20.45), the principal values are the roots of the cubic
equation. AI3+BI2+CI +D=0, where
0
–40000
–20000
20 40 60
I
80 100
704
c
2008 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
Problem 20.97 For the object in Problem 20.81, deter-
0.1 m0.1 m
y
x
0.1 m
0.2 m
Solution: In Problem 20.81, we found the inertia matrix to be
0.00667 −0.01 0
000.08 −I
I1=0.08 kg-m2,I
2=0.0748 kg-m2,I
3=0.0052 kg-m2.
Substituting these principal inertias into Eqs. (20.46) and dividing the
Problem 20.98 The 1-kg, 1-m long slender bar lies in
the x′–y′plane. Its moment of inertia matrix is
1
12 sin2β−1
12 sin βcos β0
Use Eqs. (20.45) and (20.46) to determine the princi-
pal moments of inertia and unit vectors parallel to the
corresponding principal axes.
y’
principal value will be zero, and the associated principal axis will
coincide with the slender bar. Since the moments of inertia about the
preliminary results.]
Principal Moments of Inertia: The moments and products:
A=+1,
B=−(Ix′x′+Iy′y′+Iz′z′)=−sin2β
D=−(Ix′x′Iy′y′Iz′z′−Ix′x′I2
y′z′−Iy′y′I2
x′z′−Iz′z′I2
x′y′
−2Ix′y′Iy′z′Ix′z′),
the solution of the quadratic I2+2bI +c=0 where b=−1
12 ,c=
1
144 , from which I1,2=−b±√b2−c=1
12 , from which I2=1
12 ,
V(j )
y=Ix′y′(Iz′z′−Ij)+Ix′z′Iy′z′
V(j )
|V(1)|=|cos β|
144 cos2β+sin2β=|cos β|
144 ,
and the unit vector is e1=sgn(cos β)(cos βi+sin βj), where
Eq. (20.46) fails for the repeated principal values, and the charac-
teristic vectors are to determined from the condition of orthogonality
with e1. From the preliminary discussion, e2=−isin β+jcos β
706
Problem 20.99* The mass of the homogeneous thin
plate is 3 slugs. For a coordinate system with its origin
at O, determine the plate’s principal moments of inertia
and unit vectors parallel to the corresponding principal
axes.
x’
y’
z’
2 ft
3 ft
4 ft
O
Solution: Divide the plate into Aand Bsheets, as shown. Denote
The coordinates of the center of mass of Bare
I(A)
x′y′=dxdymA=1.5 slug-ft2,
I(A)
x′z′=0,I(A)
y′z′=0.
The moments and products of inertia for plate Bare
I(B)
x′x′=mBb2
12 +(d2
y+d2
z)mB=10.67 slug-ft2,
I(B)
y′y′=mB(c2+b2)
12 +(d2
x+d2
z)mB=16.67 slug-ft2,
I(B)
z′z′=mBc2
12 +(d2
x+d2
y)mB=6 slug-ft2,I(B)
x′y′=0,
I(B)
x′z′=dxdzmB=6 slug-ft2,I(B)
y′z′=0.
The inertia matrix is the sum of the two matrices:
[I′]=
Ix′x′−Ix′y′−Ix′z′
−Iy′x′Iy′y′−Iy′z′
−Iz′x′−Iz′y′Iz′z′
=
12 −15 −6
−1.519.67 0
−6010.33
.
z‘
05
10 15
I
Zero Crossings
20 25
=524.97,
Principal axes: The characteristic vectors parallel to the principal axes
are obtained from Eq. (9.20),
708
Problem 20.100 The disk is pinned to the horizontal
shaft and rotates relative to it with angular velocity ω0.
Relative to an earth-fixed reference frame, the vertical
shaft rotates with angular velocity ω0.
(a) Determine the disk’s angular velocity vector ωrel-
ative to the earth-fixed reference frame.
(b) What is the velocity of point Aof the disk relative
to the earth-fixed reference frame?
θ
b
A
x
R
z
y
ω
0
ω
d
008.333 ×105
For rotation at a constant rate, the angular acceleration is zero,
α=0. The body-fixed coordinate system rotates with angular velocity
MOz
=
00.01047 0
×
4.167 ×1052.5×1050
2.5×1054.167 ×1050
×
0.01047
0
Problem 20.101 The disk is pinned to the horizon-
tal shaft and rotates relative to it with constant angular
velocity ω0. Relative to an earth-fixed reference frame,
the vertical shaft rotates with constant angular veloc-
ity ω0. What is the acceleration of point Aof the disk
relative to the earth-fixed reference frame?
710
Problem 20.102 The cone is connected by a ball-and-
socket joint at its vertex to a 100-mm post. The radius
of its base is 100 mm, and the base rolls on the floor.
The velocity of the center of the base is vC=2k(m/s).
(a) What is the cone’s angular velocity vector ω?
(b) What is the velocity of point A?
x
100 mm
A
y
z
C
60°
400 mm
Solution: Denote θ=60◦,h=0.1m,L=0.4m,R=0.1m.
y
Problem 20.103 The mechanism shown is a type of
universal joint called a yoke and spider. The axis Llies
in the x–zplane. Determine the angular velocity ωLand
the angular velocity vector ωSof the cross-shaped “spi-
der” in terms of the angular velocity ωRat the instant
shown.
2b
2b
y
z
L
x
φ
ω
L
ω
R
712