Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
2-30.
X
P(X)
X · P(X)
0
0.05
0.00
1
0.15
0.15
2-31.
X
P(X)
X · P(X)
X – E(X)
(X – E(X))2
(X – E(X))2P(X)
1
0.05
0.05
–4.45
19.803
0.99013
2
0.05
0.1
–3.45
11.903
0.59513
3
0.10
0.3
–2.45
6.003
0.60025
2-32. This is a binomial distribution with n = 10, p = 0.5, q = 0.5
a)
( ) ( ) ( ) ( )
7 10 7
10!
7 0.5 0.5 0.1172
7! 10 7 !
Pr −
= = =
−
= 0.1719
2-33. This is a binomial distribution with n=4, p=0.7, and q=0.3.
3 4 3
4!
−
2-34. This is a binomial distribution with n =5, p=0.1, and q=0.9.
1 5 1
5!
−
2-35. This is a binomial distribution with n=6, p=0.05, and q=0.95.
6!
2-36. This is a binomial distribution with n=6, p=0.15, and q=0.85.
( ) ( ) ( ) ( )
0 6 0
6!
0 0.15 0.85 0.377
0! 6 0 !
Pr
−
= = =
−
2-37.
= 450 degrees
= 25 degrees
X = 475 degrees
The area to the left of 475 is 0.8413 from Table 2.9, where
= 1. The area to the right of 475
is 1 – 0.84134 = 0.15866. Thus, the probability of the oven getting hotter than 475 is 0.1587.
area X1 = 0.65542
Z2 =
470 450 20 0.8
25 25
−==
area X2 = 0.78814
2-38.
= 4,700;
= 500
a. The sale of 5,500 oranges (X = 5,500) is the equivalent of some Z value which may be
obtained from
Z =
X
−
b.
c.
d.
Z =
4,300 4,700 400 0.8
500 500
−= − = −
2-39.
= 87,000
= 4,000
X = 81,000
2-40.
= 457,000
Ninety percent of the time, sales have been between 460,000 and 454,000 pencils. This means
that 10% of the time sales have exceeded 460,000 or fallen below 454,000. Since the curve is
X = 460,000
= 457,000
is unknown
Z = 1.64
2-41. The time to complete the project (X) is normally distributed with
= 60 and
= 4.
a) P(X 62) = P(Z (62 – 60)/4) = P(Z 0.5) = 0.69146
b) P(X 66) = P(Z (66 – 60)/4) = P(Z 1.5) = 0.93319
2-42. The time to complete the project (X) is normally distributed with
= 40 and
= 5. A
penalty must be paid if the project takes longer than the due date (or if X due date).
a) P(X 40) = 1 – (X 40) = 1 – P(Z (40 – 40)/5) = 1 – P(Z 0) = 1 – 0.5 = 0.5
P(X due date) = 0.95 or
P(X _____) = 0.95
The Z-value for a probability of 0.95 is approximately 1.64, so the due date (X) should
have a Z-value of 1.64. Thus,
2-43. = 5/day; e– = 0.0067 (from Appendix C)
a.
( ) ( )( )
1 0.0067
0 0.0067
!1
xe
PX
−
= = =
( ) ( )( )
5 0.0067
1 0.0335
1
P==
b. These sum to 0.6125, not 1, because there are more possible arrivals. For example, 6 or 7
patients might arrive in one day.
2-44. P(X 3) = 1 – P(X 3) = 1 – [P(0) + P(1) + P(2) + P(3)]
2-45.
= 3/hour
a. Expected time =
11
hour
3
=
2-46. Let S = steroids present
N = steroids not present
TP = test is positive for steroids
2-47. Let G = market is good
P = market is poor
PG = test predicts good market
PP = test predicts poor market
2-48. Let W = candidate wins the election
L = candidate loses the election
PW = poll predicts win
( ) ( )
( )
( )
( )
( )
( )
( )
( ) ( )
0.80 0.50 0.89
0.80 0.50 0.10 0.50
P PW W P W
P W PW P PW W P W P PW L P L
=+
==
+
2-49. Let S = successful restaurant
U = unsuccessful restaurant
PS = model predicts successful restaurant
PU = model predicts unsuccessful restaurant
2-50. Let D = Default on loan; D' = No default; R = Loan rejected; R = Loan approved Given:
P(D) = 0.2
P(D') = 0.8
P(R | D) = 0.9
2-51. (a) F0.05, 5, 10 = 3.33
2-52. (a) F0.01, 15, 6 = 7.56
2-53. (a) From the appendix, P(F3,4 6.59) = 0.05, so P(F 6.8) must be less than 0.05.
(b) From the appendix, P(F7,3 8.89) = 0.05, so P(F 3.6) must be greater than 0.05.
(c) From the appendix, P(F20,20 2.12) = 0.05, so P(F 2.6) must be less than 0.05.
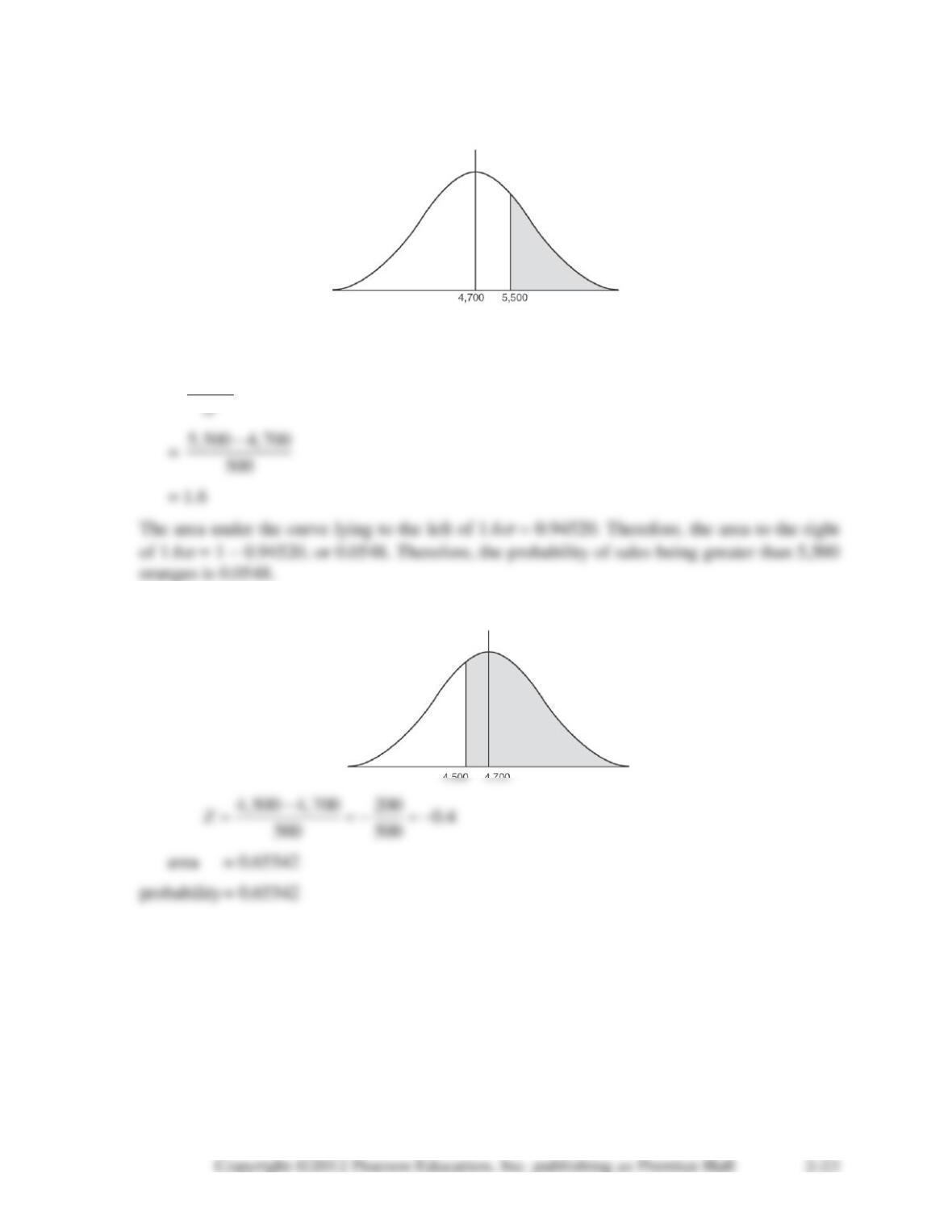
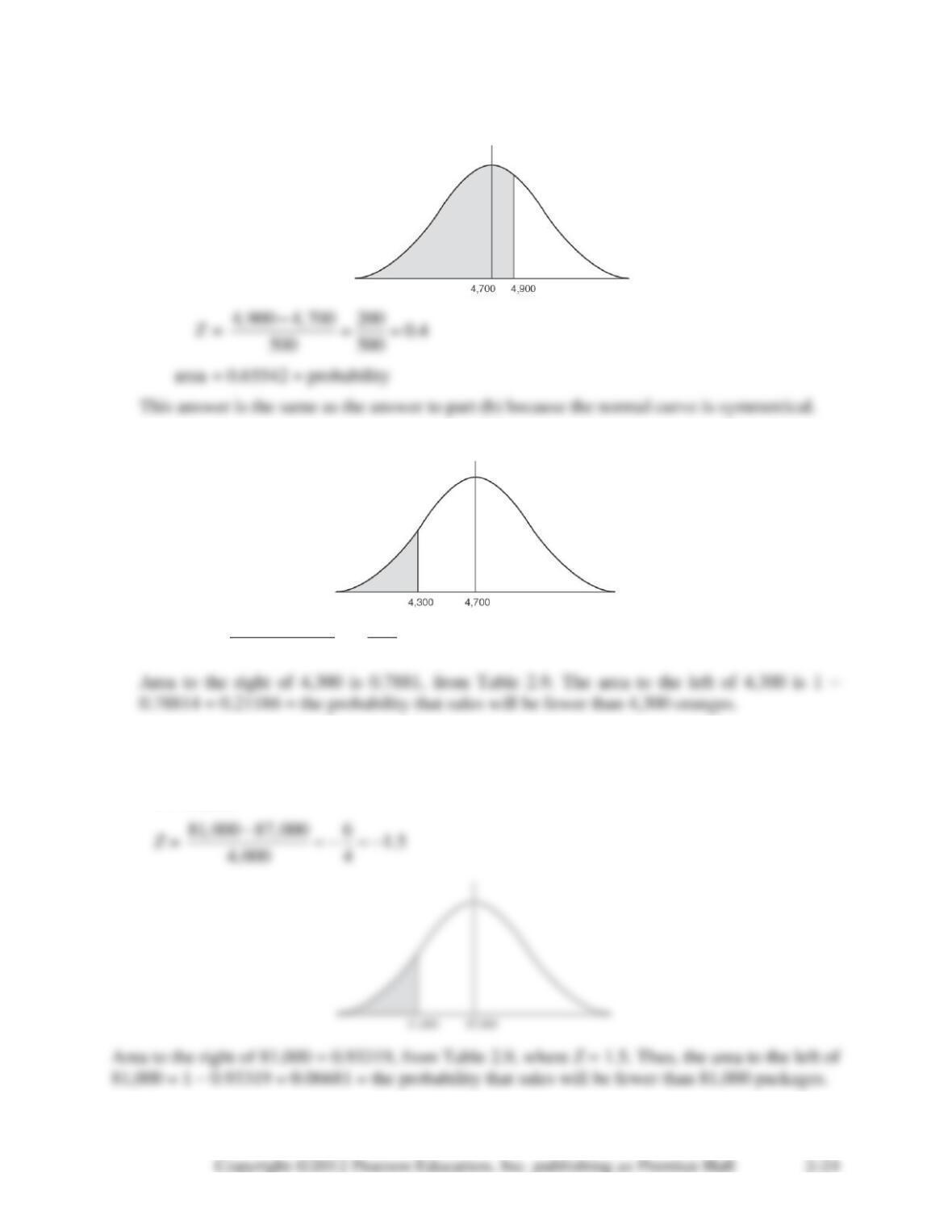
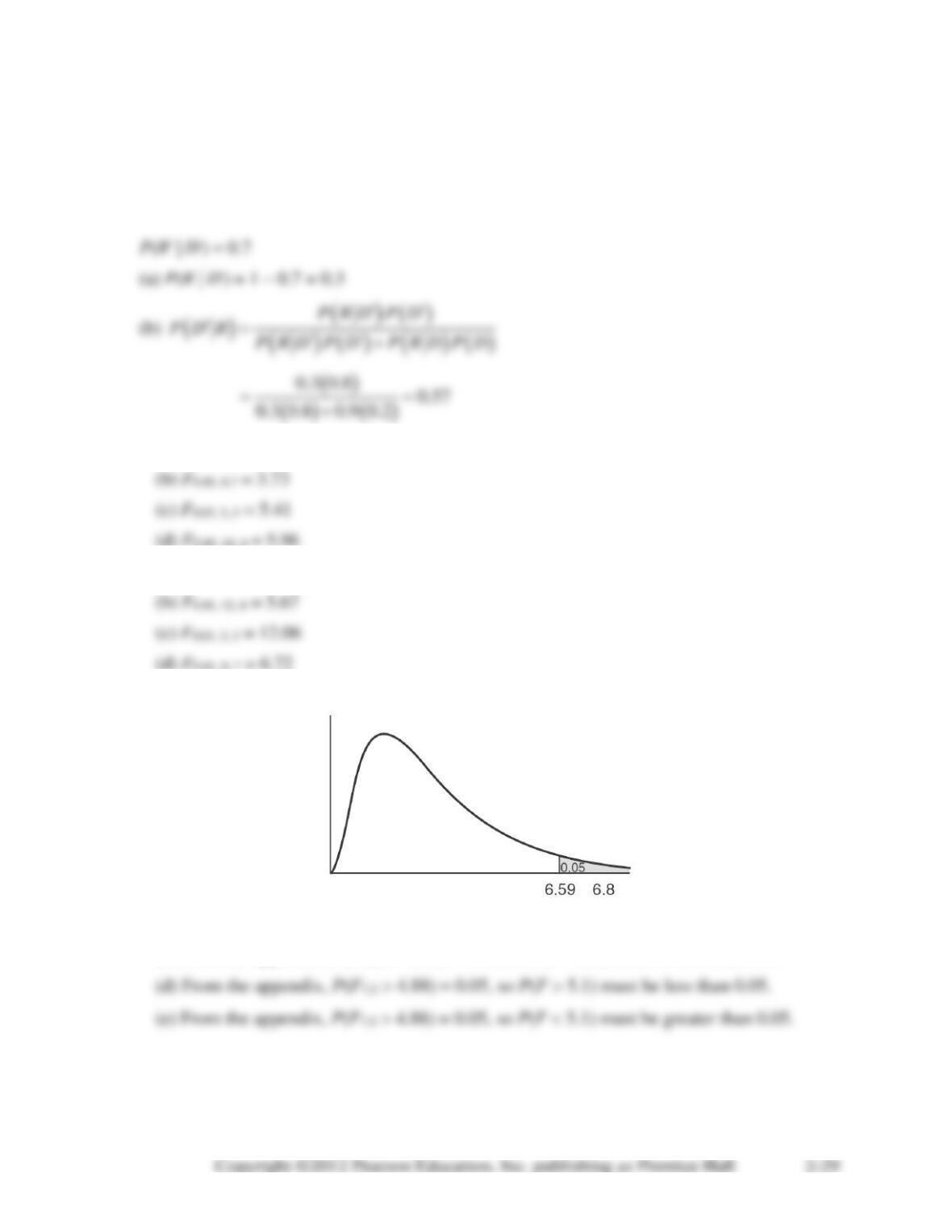
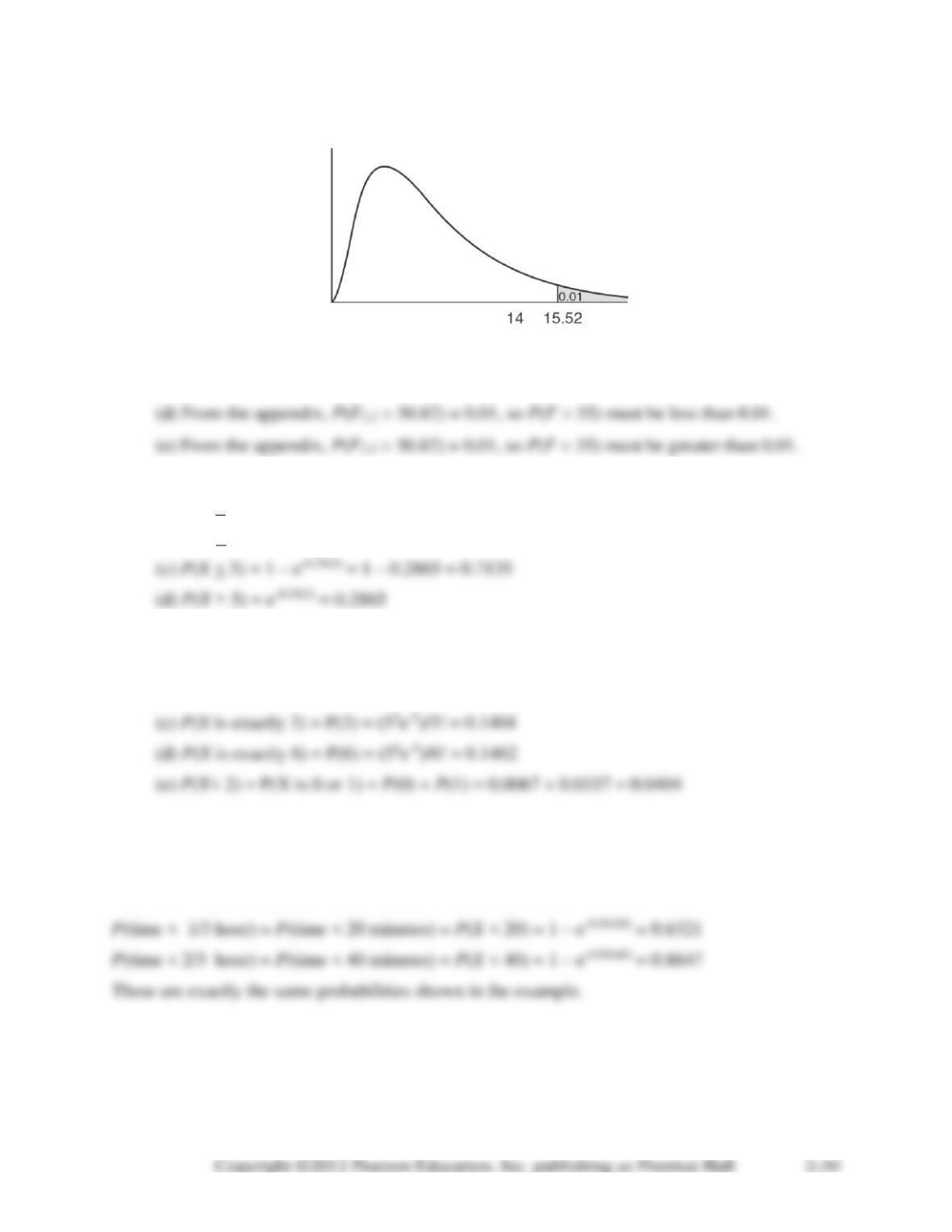
2-54. (a) From the appendix, P(F5,4 15.52) = 0.01, so P(F 14) must be greater than 0.01.
(b) From the appendix, P(F6,3 27.91) = 0.01, so P(F 30) must be less than 0.01.
(c) From the appendix, P(F10,12 4.30) = 0.01, so P(F 4.2) must be greater than 0.01.
2-55. Average time = 4 minutes = 1/µ. So µ = ¼ = 0.25
(a) P(X < 3) = 1 – e-0.25(3) = 1 – 0.4724 = 0.5276
(b) P(X < 4) = 1 – e-0.25(4) = 1 – 0.3679 = 0.6321
2-56. Average number per minute = 5. So λ = 5
(a) P(X is exactly 5) = P(5) = (55e-5)/5! = 0.1755
(b) P(X is exactly 4) = P(4) = (54e-5)/4! = 0.1755
2-57. The average time to service a customer is 1/3 hour or 20 minutes. The average number that
would be served per minute (µ) is 1/20 = 0.05 per minute.
P(time < ½ hour) = P(time < 30 minutes) = P(X < 30) = 1 – e-0.05(30) = 0.7769
2-58. X = 280
= 250
= 1.20 standard deviations
2-59. The probability of sales being over 265 boats:
X = 265
= 250
= 0.60
0.60. This area is 1 – 0.72575, or 0.27425. Therefore, the probability of selling more than 265
boats = 0.2743.
For a sale of fewer than 250 boats:
2-60.
= 0.55 inch (average shaft size)
X = 0.65 inch
= 0.10 inch
Converting to a Z value yields
We thus need to look up the area under the curve that lies to the left of 1
. From Table 2.9, this
is seen to be = 0.84134. As seen earlier, the area to the left of
is = 0.5000.
2-61. Greater than 0.65 inch:
= 0.15866
Thus, the probability of a shaft size being greater than 0.65 inch is 0.1587.
Converting to scores:
1
1
X
Z
−
=
2
2
Z
X
−
=
Since Table 2.9 handles only positive Z values, we need to calculate the probability of the shaft
size being greater than 0.55 + 0.02 = 0.57 inch. This is determined by finding the area to the left
of 0.57, that is, to the left of 0.2. From Table 2.9, this is 0.57926. The area to the right of 0.2
0.23468. The probability that the shaft will be between 0.53 inch and 0.59 inch is 0.2347.
X
Z
−
=
Thus, we need to find the area to the left of –1
. Again, since Table 2.9 handles only positive
values of Z, we need to determine the area to the right of 1
. This is obtained by 1 – 0.84134 =
0.15866 (0.84134 is the area to the left of 1
). Therefore, the area to the left of –1
= 0.15866
(the curve is symmetrical). Thus, the probability that the shaft size will be under 0.45 inch is
0.1587.
2-62.
x n x
npq
x
−
x = 3
n = 4
2-63. Probability one will be fined =
P(2) + P(3) + P(4) + P(5)
= 1 – P(0) – P(1)
2-64.
X
P(X)
0
( ) ( )
05
5.2 .8 .327
0
=
.327
1
( ) ( )
1 5 1
5.2 .8 .410
1
−
=
.410
1.0
XP(X)
X – E(X)
(X – E(X))2
(X – E(X))2P(X)
0.0
–.9985
.997
.326
.41
.0015
0
0
.41
1.0015
1.003
.2056
Using the formulas for the binomial:
E(X) = np
= (5)(.2) = 1.0
2-65. a. n = 10; p = .25; q = .75;
10
10 xx
pq
x
−
P(X)
X
( ) ( )
0 10 0
10 .25 .75
0
−
=
.0563
0
( ) ( )
5 10 5
10 .25 .75
5
−
=
.0584
5
( ) ( )
6 10 6
10 .25 .75
6
−
=
.0162
6
( ) ( )
7 10 7
10 .25 .75
7
−
=
.0031
7
b. E(X) = (10).25 = 2.5
2 = npq = (10)(.25)(.75)
= 1.875
SOLUTION TO WTVX CASE
1. The chances of getting 15 days of rain during the next 30 days can be computed by using the
binomial theorem. The problem is well suited for solution by the theorem because there are two
and only two possible outcomes (rain or shine) with given probabilities (70% and 30%,
respectively). The formula used is:
Probability of r successes =
( )
( )
!
!!
r n r
npq
r n r
−
−
where
n = the number of trials (in this case, the number of days = 30),
The probability of getting exactly 15 days of rain in the next 30 days is 0.0106 or a 1.06%
chance.
2. Joe’s assumptions concerning the weather for the next 30 days state that what happens on one
day is not in any way dependent on what happened the day before; what this says, for example, is
that if a cold front passed through yesterday, it will not affect what happens today.
