Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
CHAPTER 11
Network Models
TEACHING SUGGESTIONS
Teaching Suggestion 11.1:
The solution techniques for this chapter are easy and straightforward. Although they obtain an
Teaching Suggestion 11.2:
Teaching Suggestion 11.3:
The maximal-flow technique can be used to solve a number of interesting types of problems.
Have students develop and solve maximal-flow problems different from the ones in the chapter
and at the end of the chapter.
Teaching Suggestion 11.4:
The maximal-flow technique involves subtracting capacity along the path that is picked with
Teaching Suggestion 11.5:
Students may wonder why we put the distance in a box by the node that is the closest to the
Teaching Suggestion 11.6:
The shortest-route problem can be solved using several techniques, including dynamic program-
ming. This can lead to a discussion about selecting the best technique to solve a management
science problem.
ALTERNATIVE EXAMPLES
Alternative Example 11.1: Given the following network, perform the minimum-spanning tree
technique to determine the best way to connect nodes on the network, while minimizing total dis-
tance.
We begin with node 1. Node 4 is the nearest node, and thus we connect node 1 to node 4.
1.
Using the minimum-spanning tree technique, we can see that the total distance required to
connect all nodes is 18. The following figure shows the results.
Alternative Example 11.2: Given the network in the figure on the next page, determine the
maximum amount that can flow through the network.
Next, we put the maximum flow of 4 units through nodes 1, 4, and 6. The adjusted network is
shown below.
1–2–6 4 units
Alternative Example 11.3: Given the network in the following figure, determine the shortest
route or path through the network.
We continue the process. The next-nearest node to node 1 is node 5. The distance between
node 4 and 5 is 100 and the total distance between node 5 and node 1 is 200. Thus we put 200 in
a box by node 5. The results of this step are shown in the following figure.
SOLUTIONS TO DISCUSSION QUESTIONS AND PROBLEMS
11-1. The minimal-spanning technique is one that will find the best way to connect all the nodes
in a network together while minimizing the total distance between nodes or the total cost of con-
11-2. The first step of the maximal-flow technique involves picking any path that has some ca-
pacity through the network. Then the flow along this path is increased to the maximum. Capacity
11-3. The maximal-flow technique can be used to determine the maximum number of cars that
can flow through a road system, the number of gallons of chemicals that can flow through a
11-4. The first step of the shortest-route technique is to find the nearest node to the origin. We
put the distance in a box to help us keep track of intermediate solutions. Next, we find the next
nearest node to the origin, using any previous analysis. This process is continued until we get an
optimal solution.
11-5. The shortest-route technique can be used to find the best way to install a phone cable be-
11-6. Yes, it is possible to get alternative optimal solutions with all of the techniques discussed
in this chapter. There are, however, no automatic approaches or procedures that will alert you to
alternative optimal solutions as was the case in linear programming. In most cases, however, al-
ternative optimal solutions can be found by inspection.
11-7.
A maximal-flow problem can be modeled as a capacitated transshipment problem in which eve-
11-8.
The shortest-route problem can be modeled as a transshipment problem with only one source and
11-9.
One optimal solution is shown. Connect 1–3, 1–4, 3–6, 6–7, 1–2, 4–5, 7–9, 9–8, 9–10, 10–11,
11–13, 13–14, and 14–12. Alternate solutions can be found by substituting 3–4 for 1–4 and sub-
stituting 9–12 for 13–14. Total distance = 45.
11-10.
Flow
Path
(Cars/Hour)
1–2–5–7–8
2
11-11.
The shortest route is 1–3–5–7–10–13. The distance is 430 miles.
11-12. The minimal-spanning tree technique is needed to solve this problem. The minimum dis-
tance is 47 (4,700 feet). As you can see, the final solution has changed.
Figure for Problem 11-12
11-13. The maximal flow through the network is 7. This is higher by 2 cars from Problem 11-
10. The solution is given below.
Flow
Path
(Cars/Hour)
1–2–5–7–8
2
11-14. This is the only optimum solution to this problem (177 units of length).
11-15. There are several possible solutions. One solution is presented below.
One solution:
1–4–6 40
167 widgets per day
Alternative solutions: Substitute 1–2–4–6 for 32 in lieu of 1–4–6 or 1–4–5–6 (or for some por-
tion of the 32).
11-16. No, the changes do not have an impact on the final solution. With the changes, the opti-
mal solution still has a shortest distance of 430 miles. The final network is given below. Note
Figure for Problem 11-16
11-17. The solution to the minimal-spanning tree problem results in a minimum distance of 21
(2,100 yards). The final network follows.
Figure for Problem 11-17
11-18. If the distance between nodes 6 and 7 becomes 5, the minimum distance changes to 23
(2,300 yards). The final network follows.
11-19. The maximum number of cars that can flow from the hotel complex to Disney World is
13 (1,300 cars per hour).
Solution to Problem 11-19
Flow
1–2
3
1–3
8
1–4
2
11-20. The impact of the construction project to increase the road capacity around the outside
roads from International Drive to Disney World would increase the number of cars per hour to
1,700 per hour (17). The increase is 400 cars per hour as would be expected. The solution follows.
Solution to Problem 11-20
Flow
1–2
5
1–3
8
1–4
2
1–5
2
2–6
5
3–7
8
11-21. Let Xij = flow from node i to node j
Maximize Flow = X11,1
Subject to
X12 < 10
X48 < 2
X58 < 14
X69 < 4
X7,10 < 8
X8,10 < 3
X9,11 < 8
X10,11 < 10
X10,8 < 1
X12 = X21 + X26
X13 +X73 = X31 + X37
X14 = X47 + X48
X15 +X85 = X51 + X58
X26 = X69
Xij > 0 and integer for all i and j
Solving this on the computer shows a capacity of 13. There are multiple optimal solutions. For
11-22. The capacities would increase by 2 along the paths 1-2-6-9-11 and 1-5-8-10-11. These
would result in changes in eight of the constraints in Problem 11-21. All other constraints would
remain unchanged. The new constraints would be:
X12 < 12
X15 < 17
X26 < 5
X58 < 16
11-23. Solving this maximal flow problem results in a situation where 3,000 gallons per hour (3)
will be flowing from the origin to the final network node. The solution follows:
Solution to Problem 11-23
Flow
1–2
1
1–3
1
1–4
1
2–5
1
11-24. The impact of the emergency repair is that nodes 6 and 7 cannot be used. All flow in and
out of these nodes is 0. As a result, the flow from the origin to the final network node has been
reduced to 2,000 gallons per hour (2). The solution is shown in the following table.
Solution to Problem 11-24
Flow
1–2
1
1–4
1
2–5
1
4–8
1
11-25. The shortest route from node 1 to node 16 is 74 kilometers. The solution along with the
final network is shown in the following table and figure.
Value
1–3
15
3–7
11
7–11
18
Figure for Problem 11-25
11-26. The impact of closing two nodes (nodes 7 and 8) is to increase the shortest route from 74
to 76 kilometers. Note that all paths into and from nodes 7 and 8 have their values changed to a
very high relative number (10,000) to force these paths out of the final solution. The solution
along with the final network is given below.
Value
1–2
20
2–6
10
Figure for Problem 11-26
11-27. Xij = 1 if the arc from node i to node j is selected; 0 otherwise.
Minimize distance = 20X12 +15X13 + 18X14 + 10X25 + 10X52 + 10X26 + 10X62 + 11X37 +
12X48 + 8X56 + 8X65 + 16X59 + 16X95 + 12X69 + 12X96 + 12X67 + 12X76 + + 22X78 + 22X87 +
Subject to
X12 + X13 + X14 = 1 node 1
X12 + X52 + X62 = X25 + X26 node 2
X13 = X37 node 3
X37 + X67 + X87 + X10,7 + X11,7 = X76 + X78 + X7,10 + X7,11 node 7
X48 + X78 + X12,8 = X87 + X8,12 node 8
X59 + X69 + X13,9 = X95 + X96 + X13,9 node 9
X7,10 + X13,10 = X10,7 + X10,13 node 10
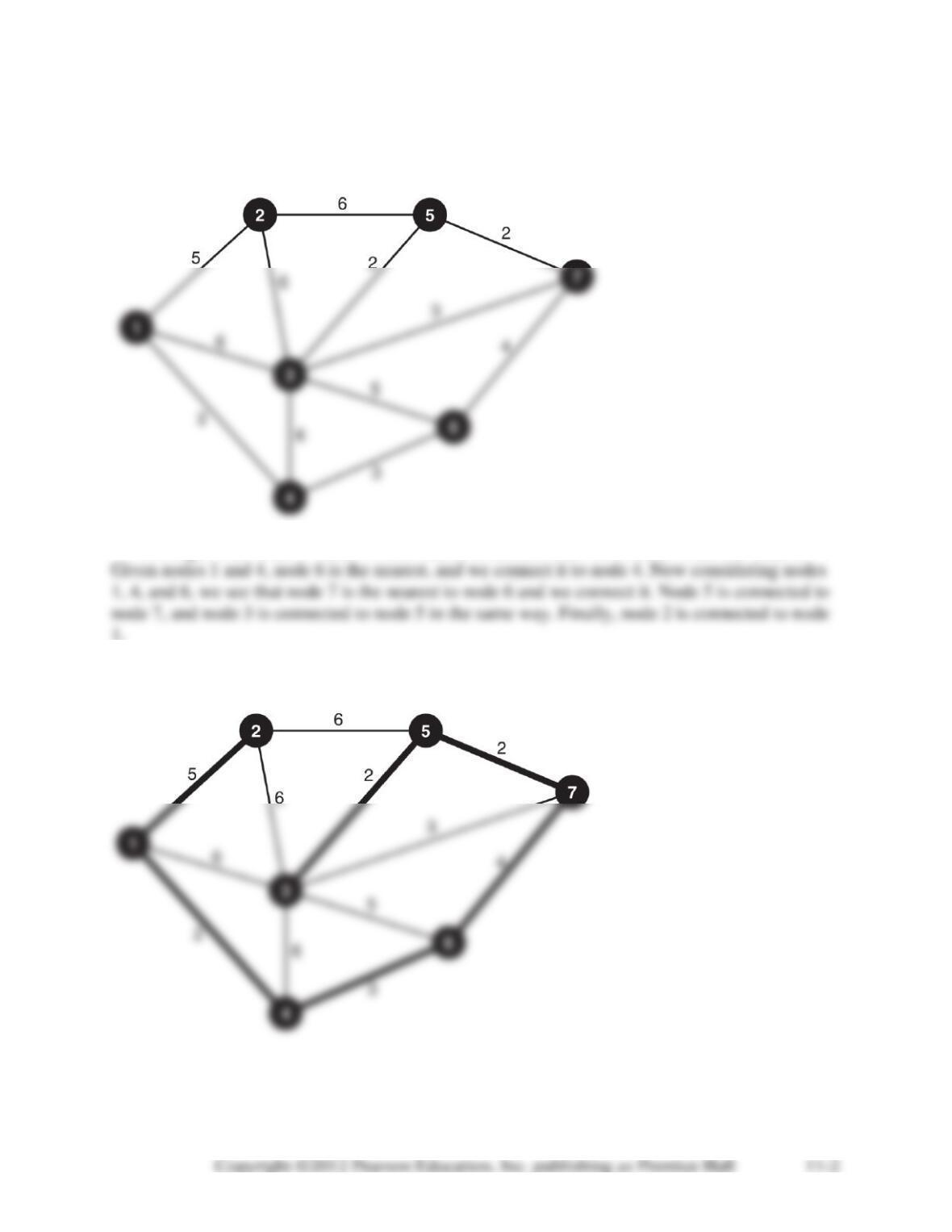
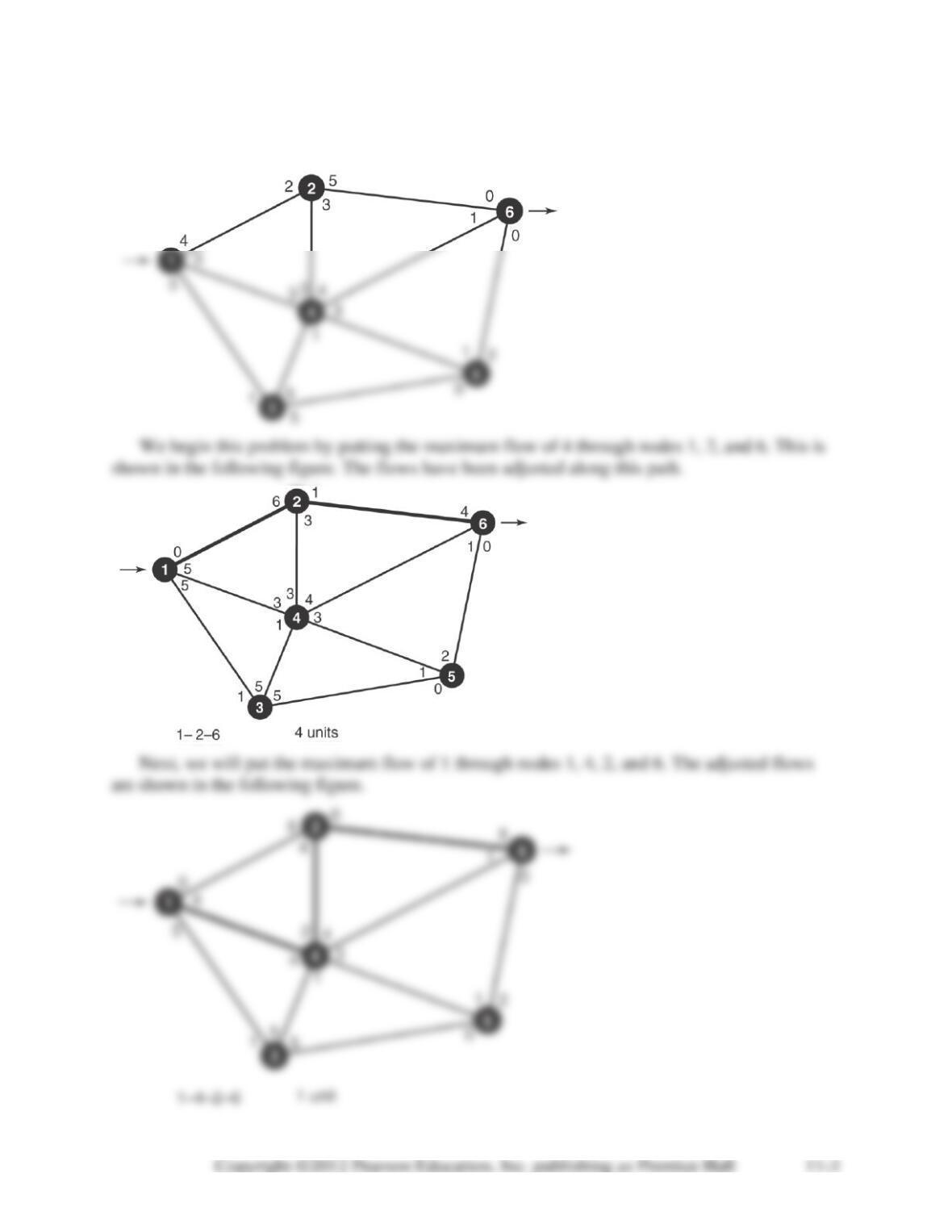
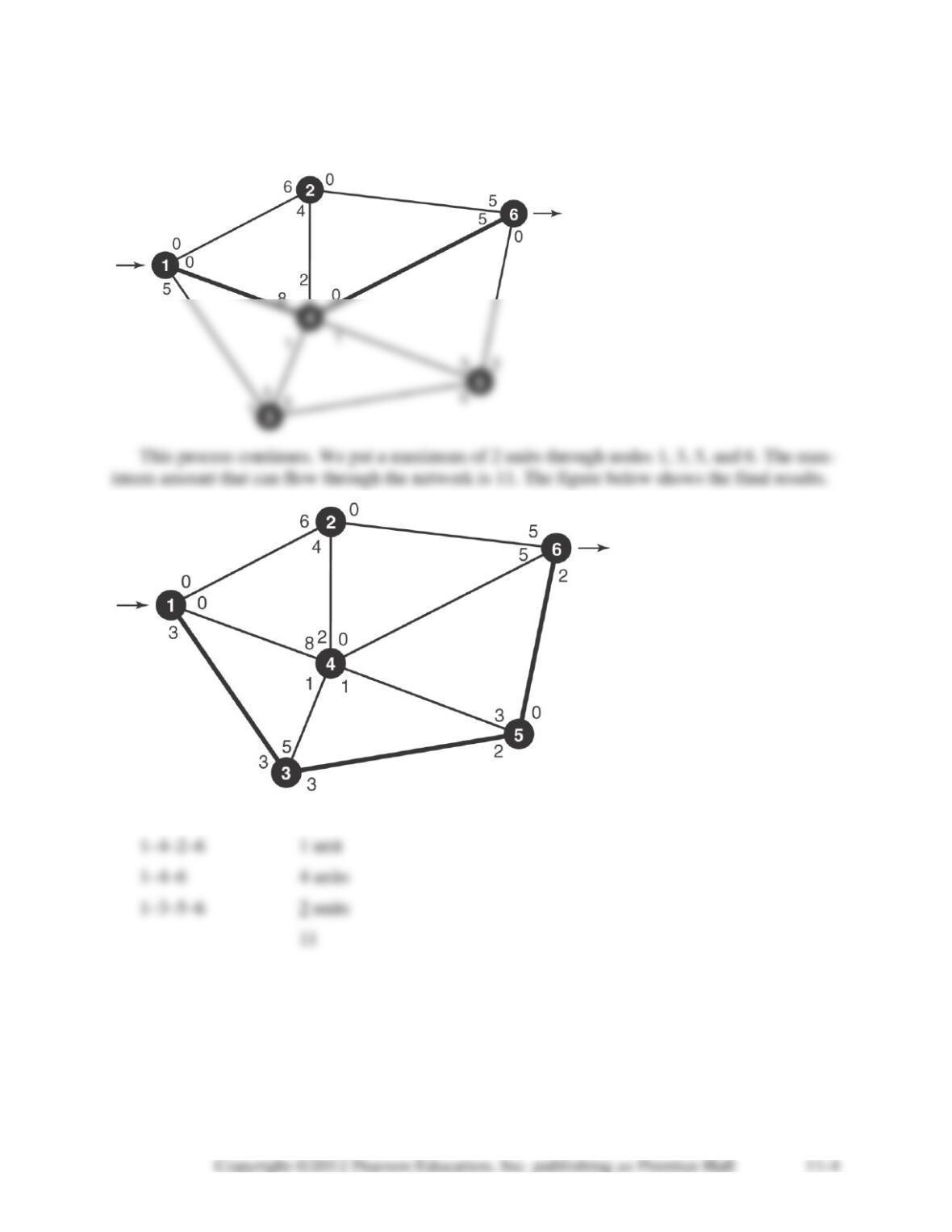
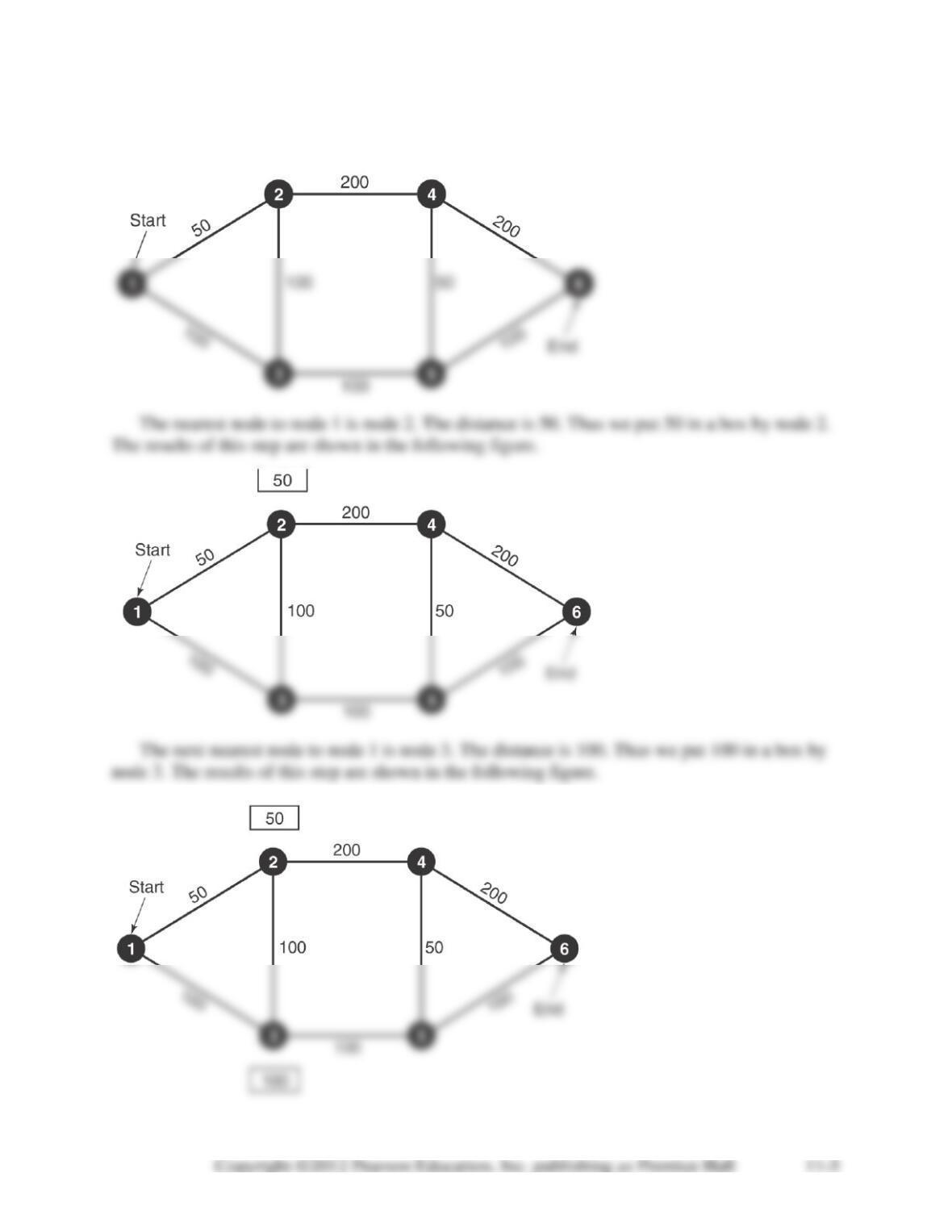
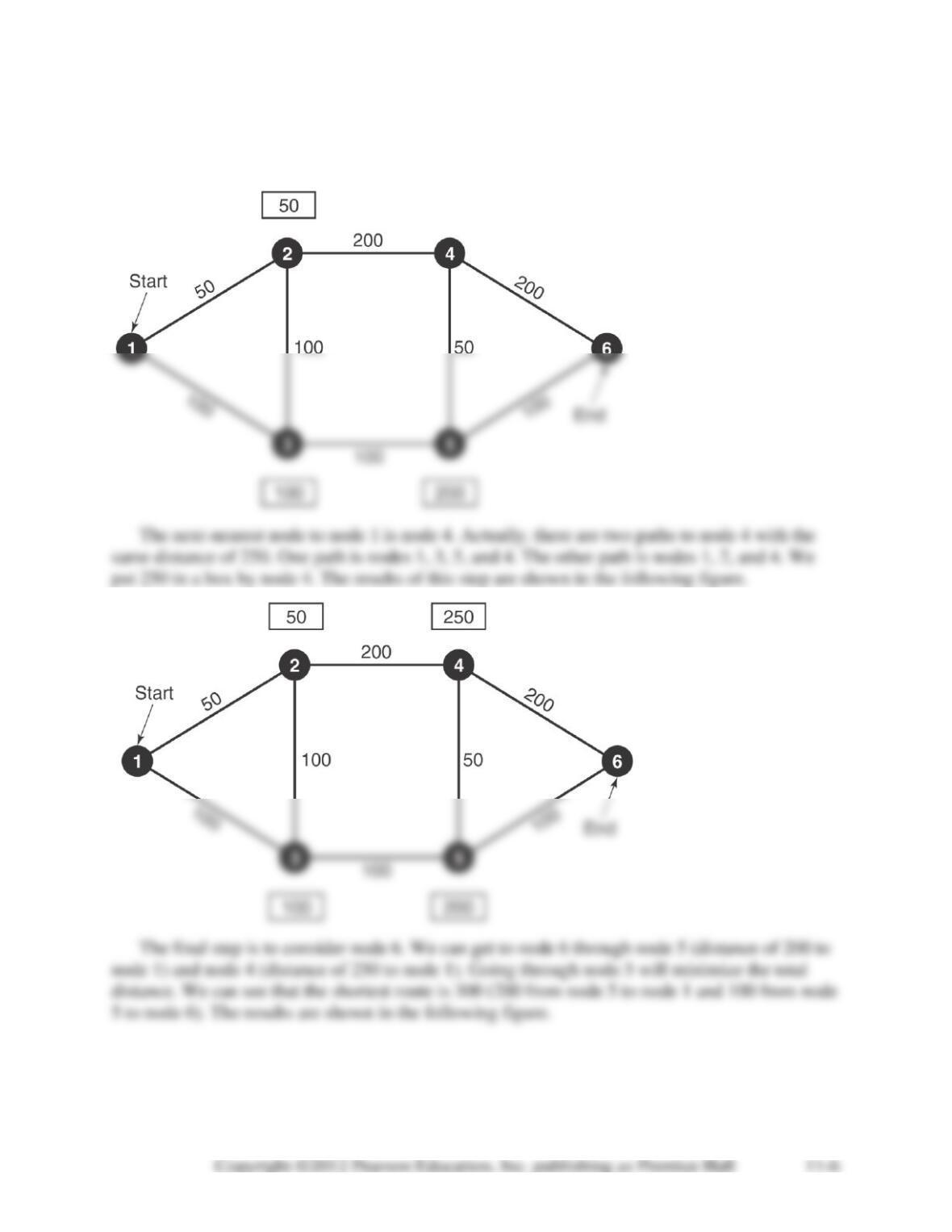
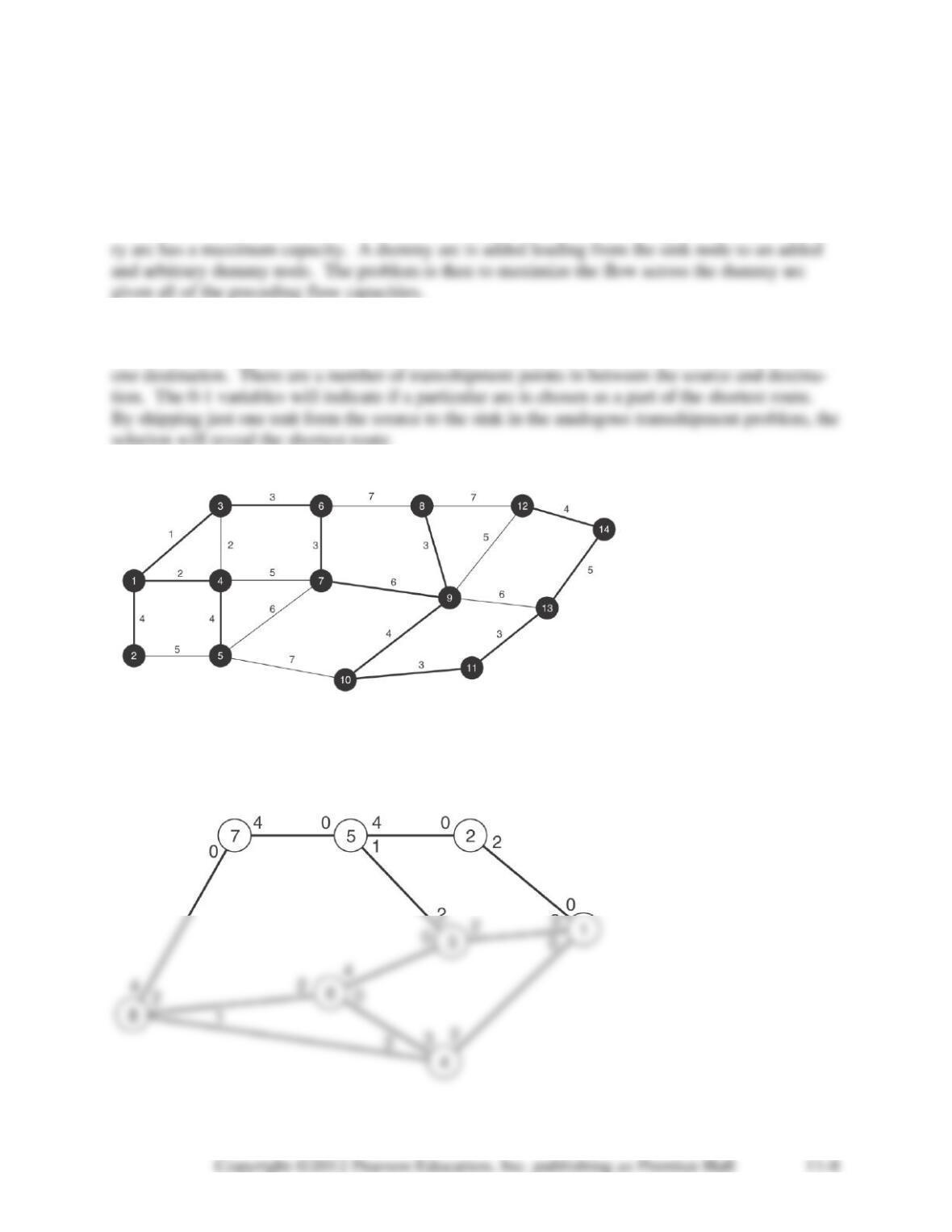
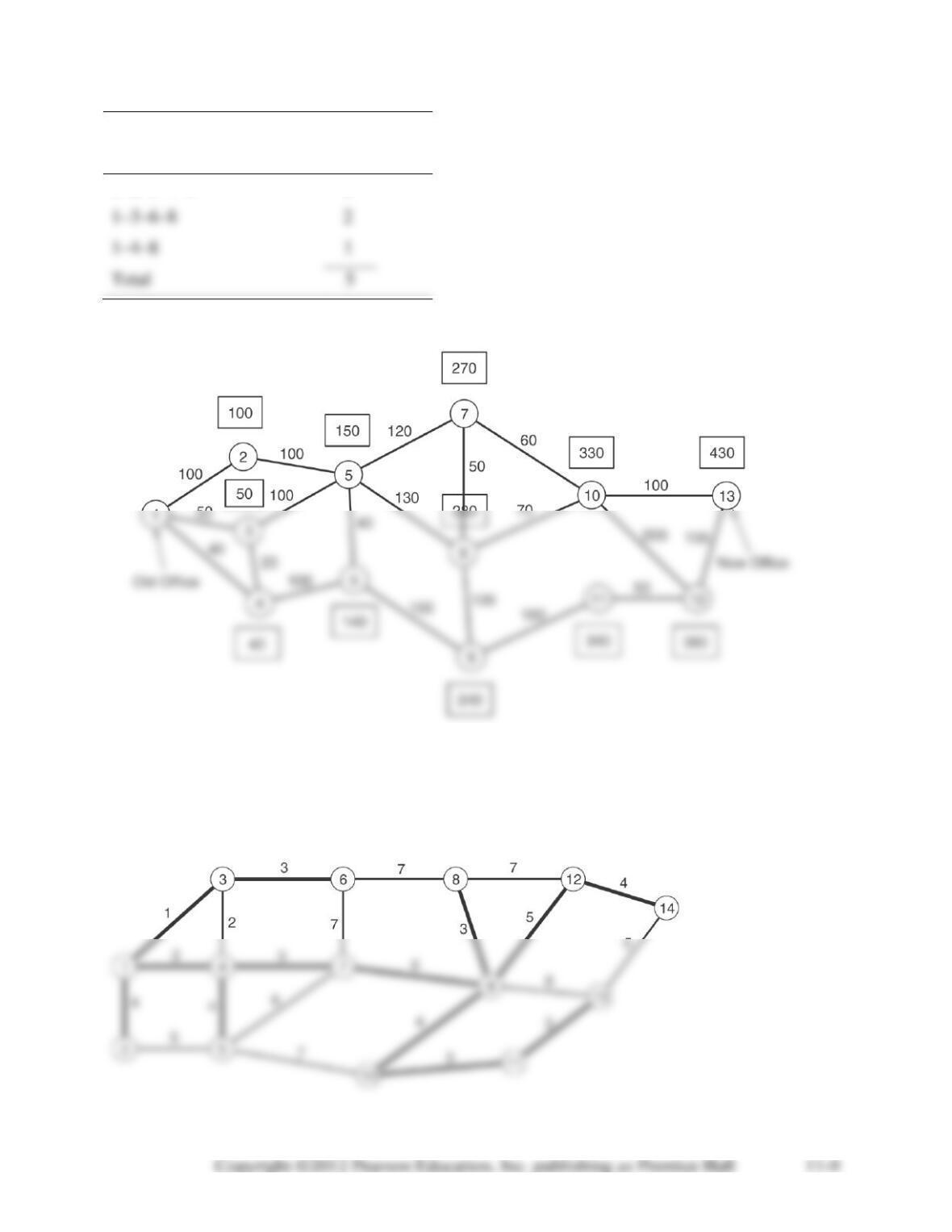
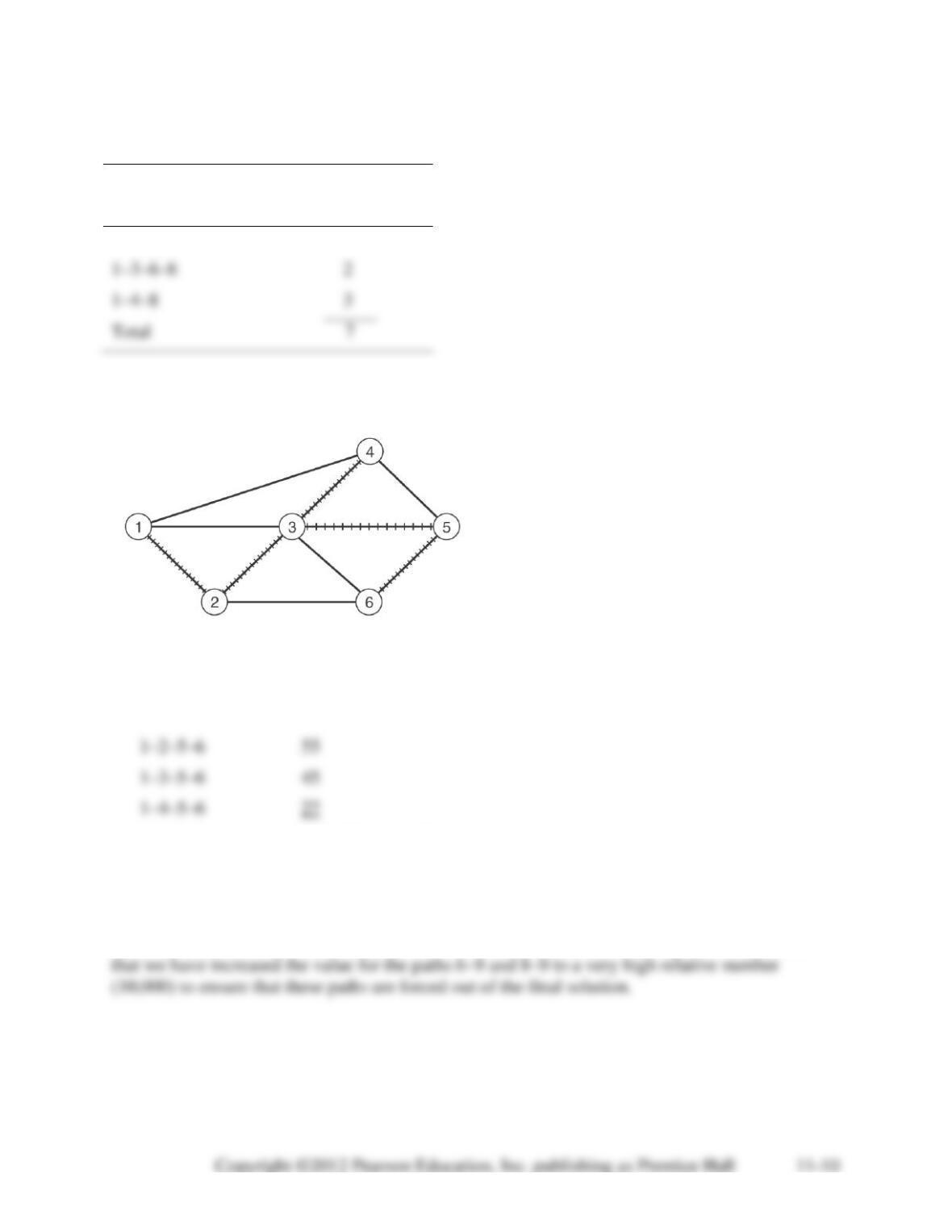
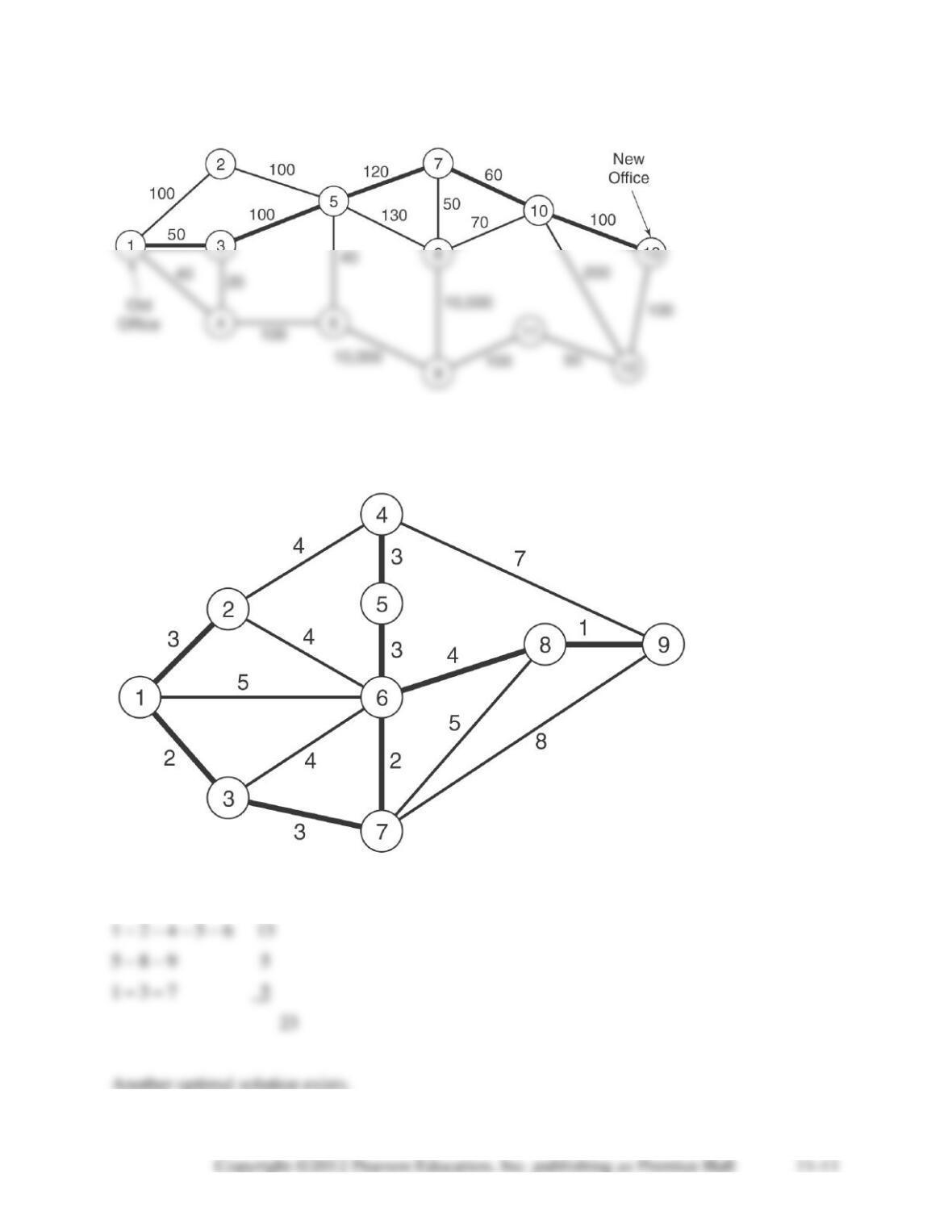
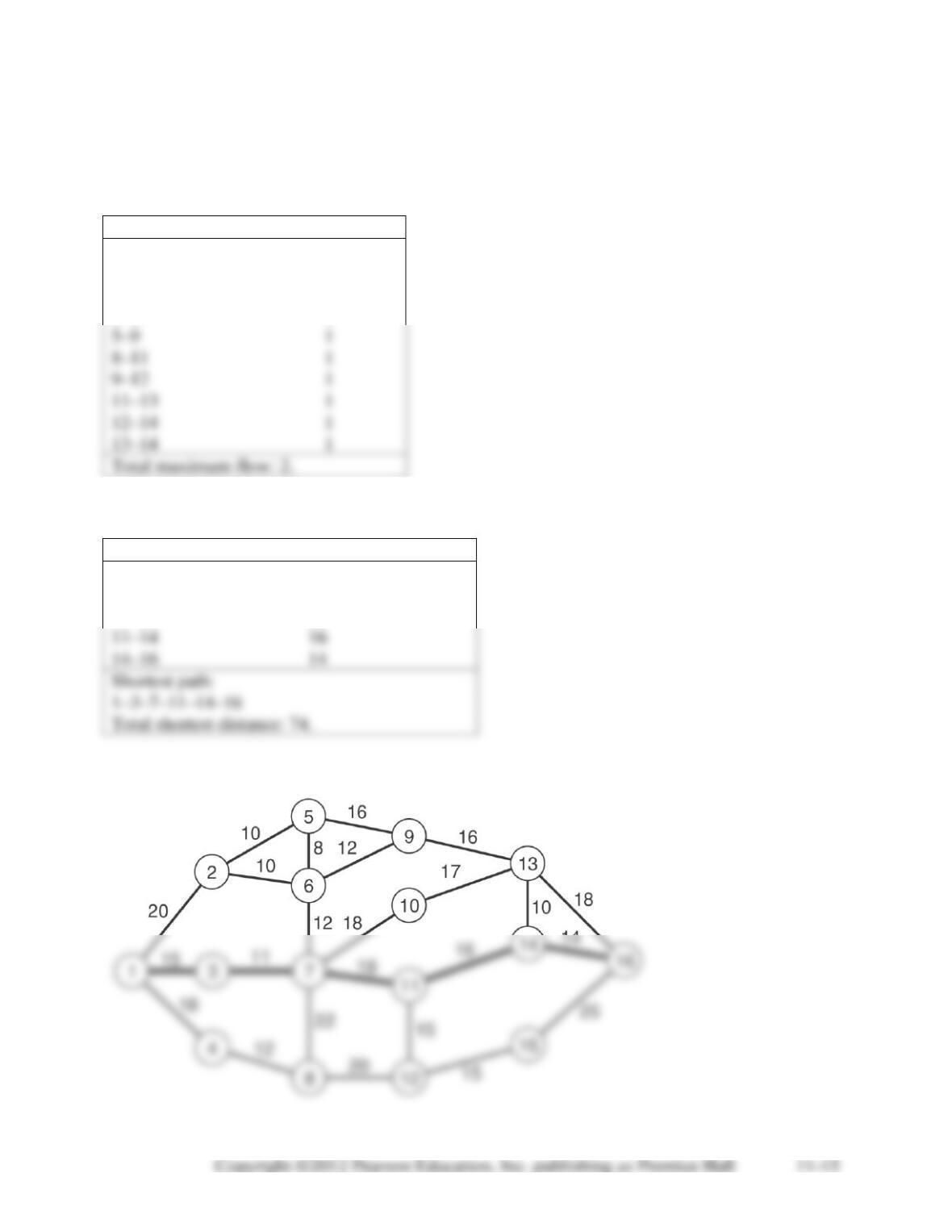
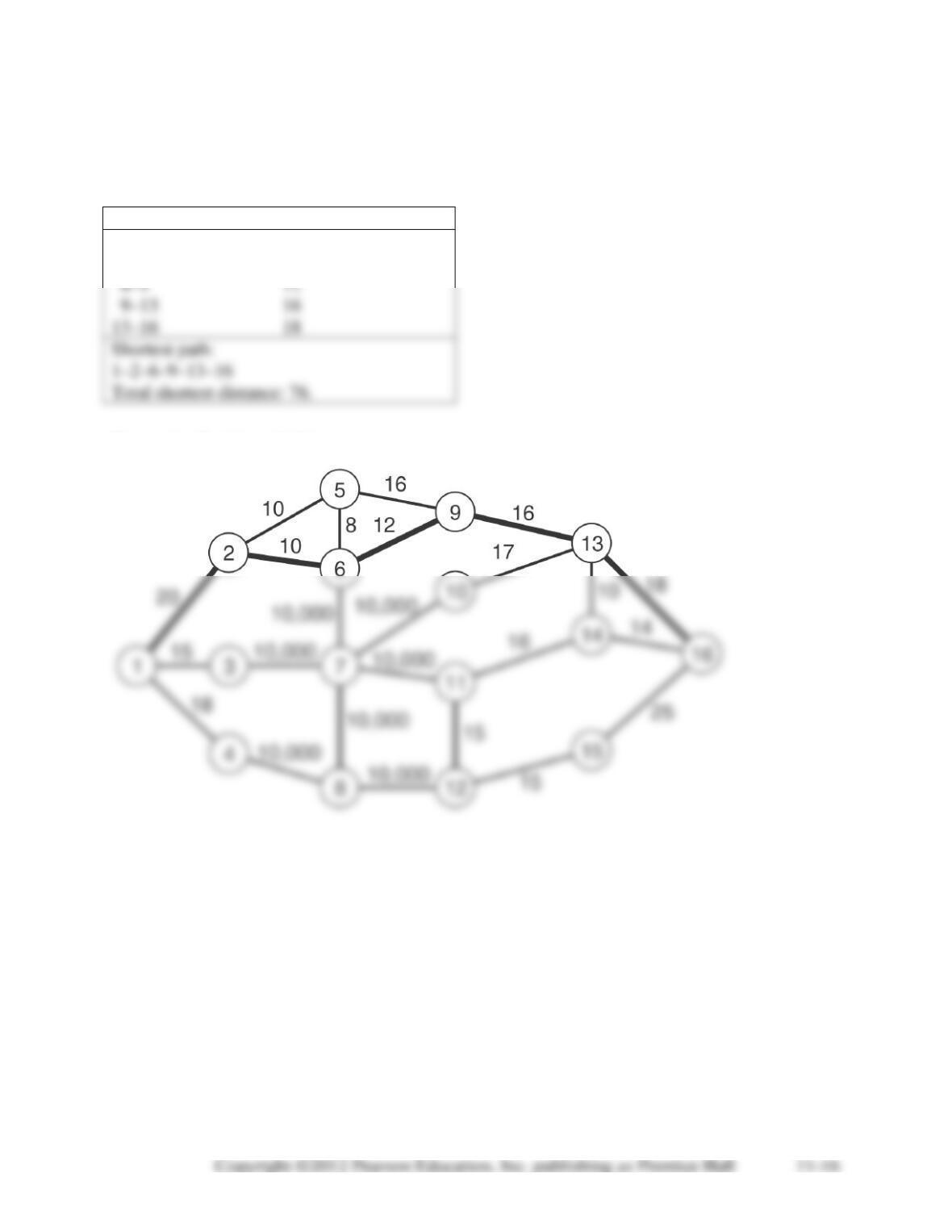
11-28. All variables representing inflow or outflow from nodes 7 and 8 (i.e. any variable with a 7
or 8 as a subscript) would be eliminated, and the constraints for these nodes would be eliminated
also. Because nodes 3, 4, and 10 each have only one arc other than the ones to nodes 7 or 8, the
variables and constraints associated with these can also be eliminated.
Minimize distance = 20X12 +10X25 + 10X52 + 10X26 + 10X62 + 8X56 + 8X65 + 16X59 + 16X95 +
Subject to
X12 + X13 + X14 = 1 node 1
X59 + X69 + X13,9 = X95 + X96 + X13,9 node 9
X12,11 + X14,11 = X11,12 + X11,14 node 11
X11,12 = X12,11 + X12,15 node 12
X13,16 + X14,16 + X15,16 = 1 node 16
All variables = 0 or 1
