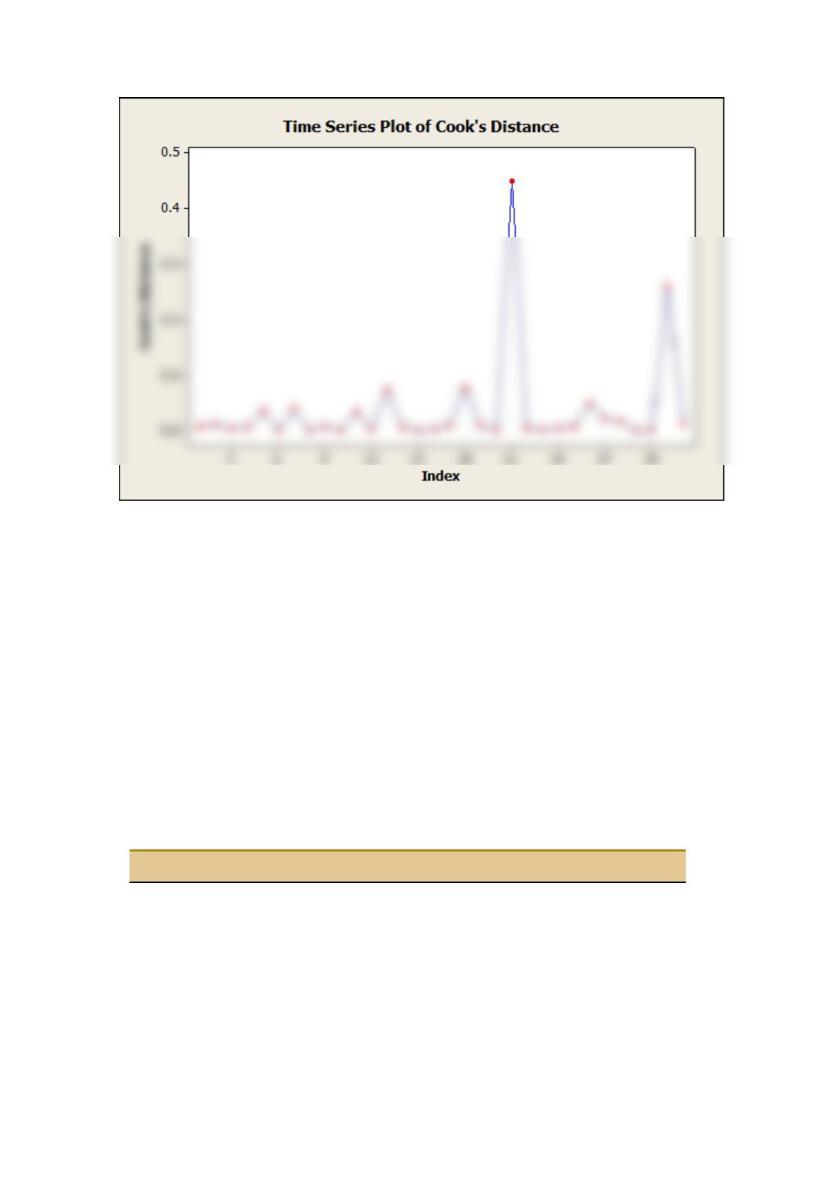
distance greater than 1, two points are different and might be further studied for influence.
Reserve Problems Chapter 12 Section 5 Problem 7
Heat treating is often used to carburize metal parts such as gears. The thickness of the carburized
layer is considered a crucial feature of the gear and contributes to the overall reliability of the
part. Because of the critical nature of this feature, two different lab tests are performed on each
furnace load. One test is run on a sample pin that accompanies each load. The other test is a
destructive test that cross-sections an actual part. This test involves running a carbon analysis on
the surface of both the gear pitch (top of the gear tooth) and the gear root (between the gear
teeth). Table given below shows the results of the pitch carbon analysis test for 32 parts.
The regressors are furnace temperature (TEMP), carbon concentration and duration of the
carburizing cycle (SOAKPCT, SOAKTIME), and carbon concentration and duration of the
diffuse cycle (DIFFPCT, DIFFTIME). The response is the result of the pitch carbon analysis test
(PITCH).