Applied Statistics and Probability for Engineers, 7th edition 2017
(a) The min Cp model is x1,x2
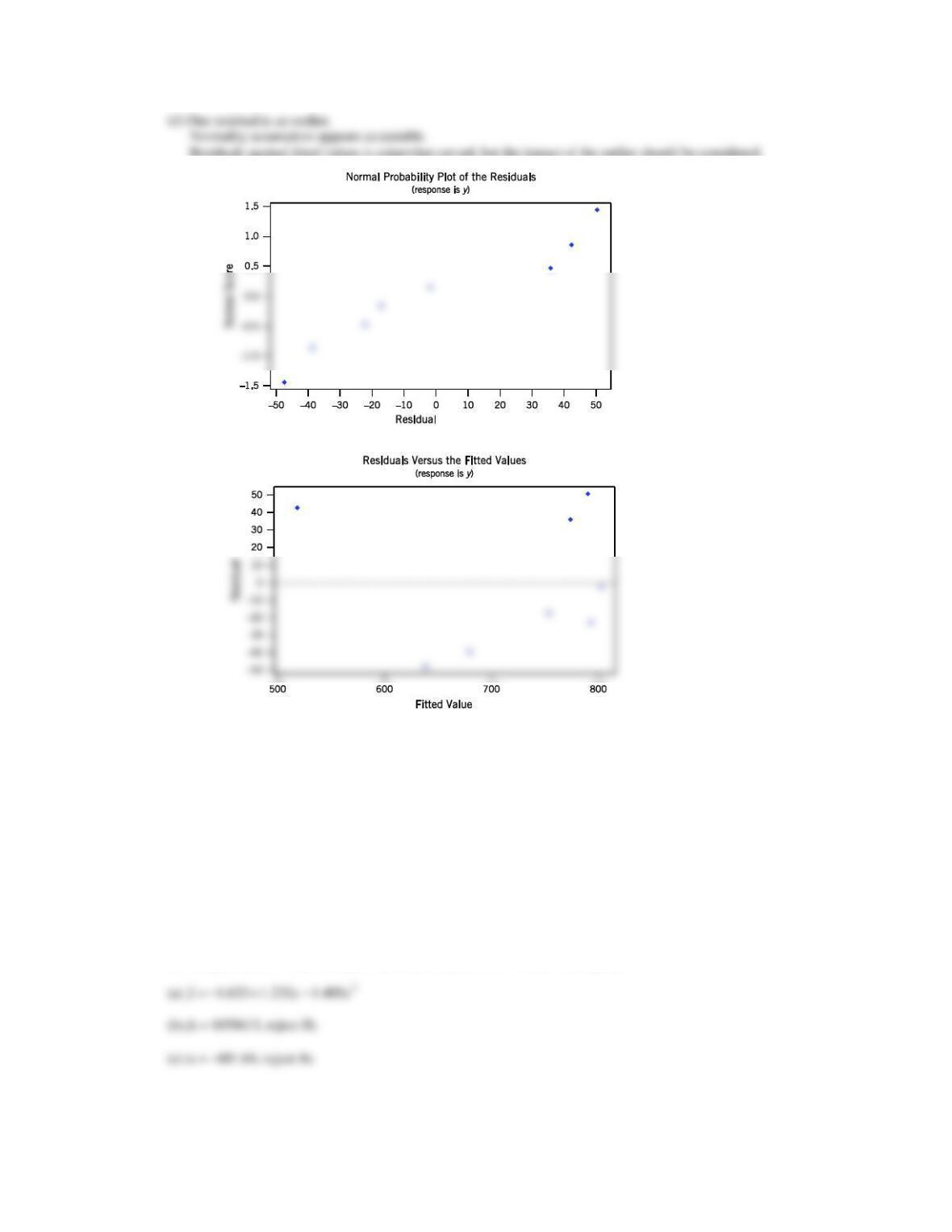
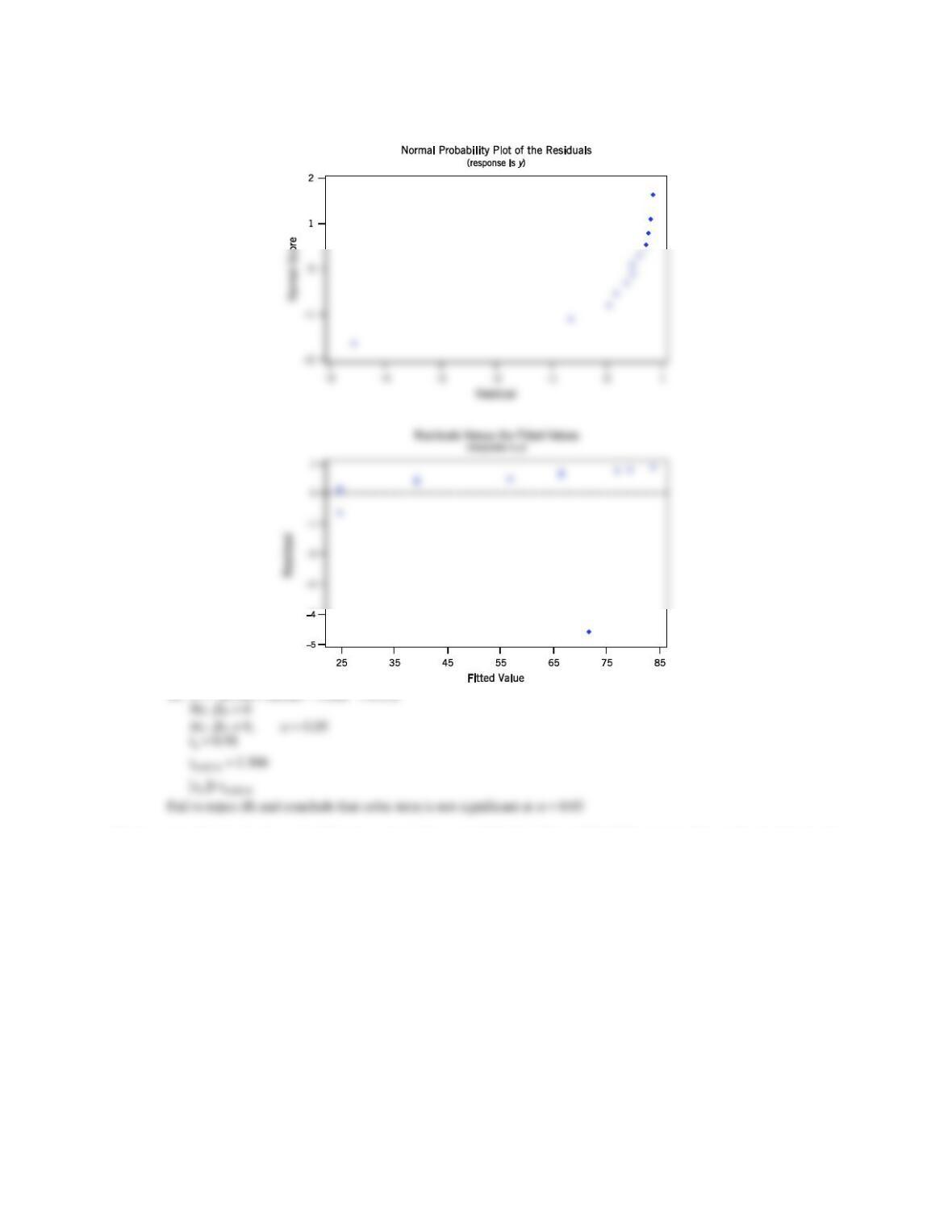
12.6.10 Consider the gray range modulation data in Exercise 12.1.11. Use the useful range as the response. Build regression
models for the data using the following techniques:
(a) All possible regressions.
(b) Stepwise regression.
(c) Forward selection.
(d) Backward elimination.
(f) Comment on the models obtained. Which model would you prefer? Why?
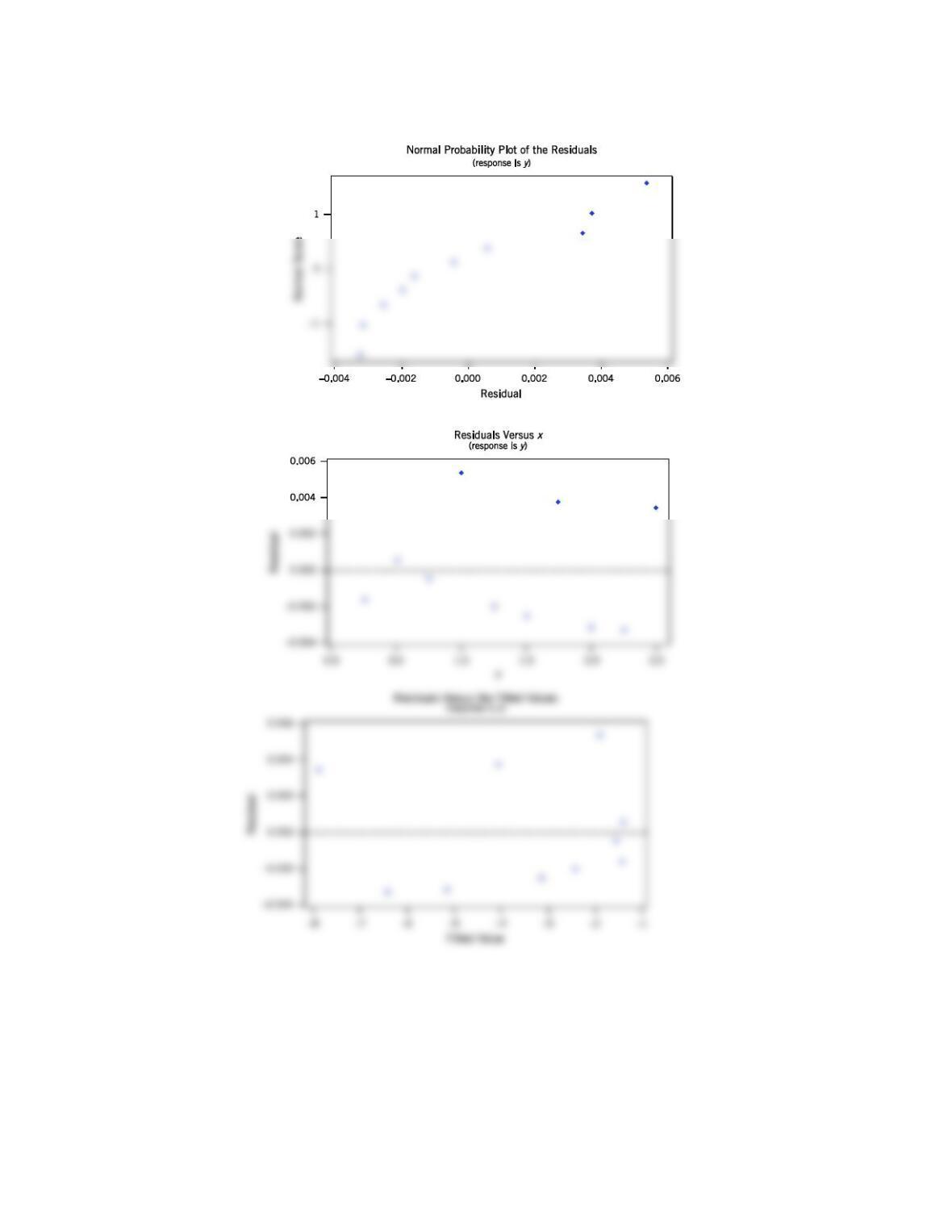
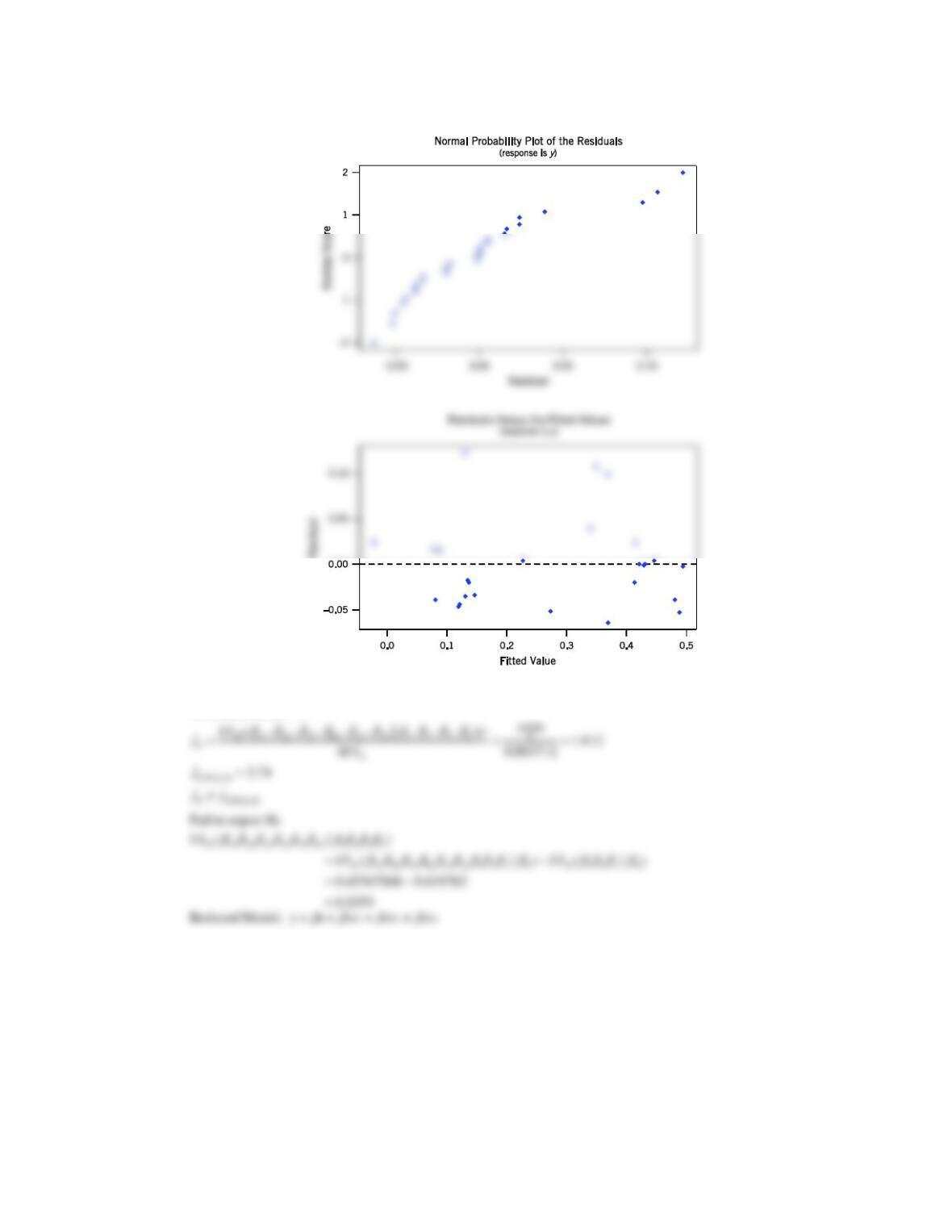
(a) The min Cp model is x2
12.6.11 Consider the NHL data in Exercise 12.1.12. Build regression models for these data with regressors GF through FG
using the following methods:
(a) All possible regressions. Find the minimum Cp and minimum MSE equations.
(b) Stepwise regression.
(c) Forward selection.
(d) Backward elimination.
(e) Which model would you prefer?
The default settings for F-to-enter and F-to-remove for Minitab were used. Different settings can change the models
generated by the method.