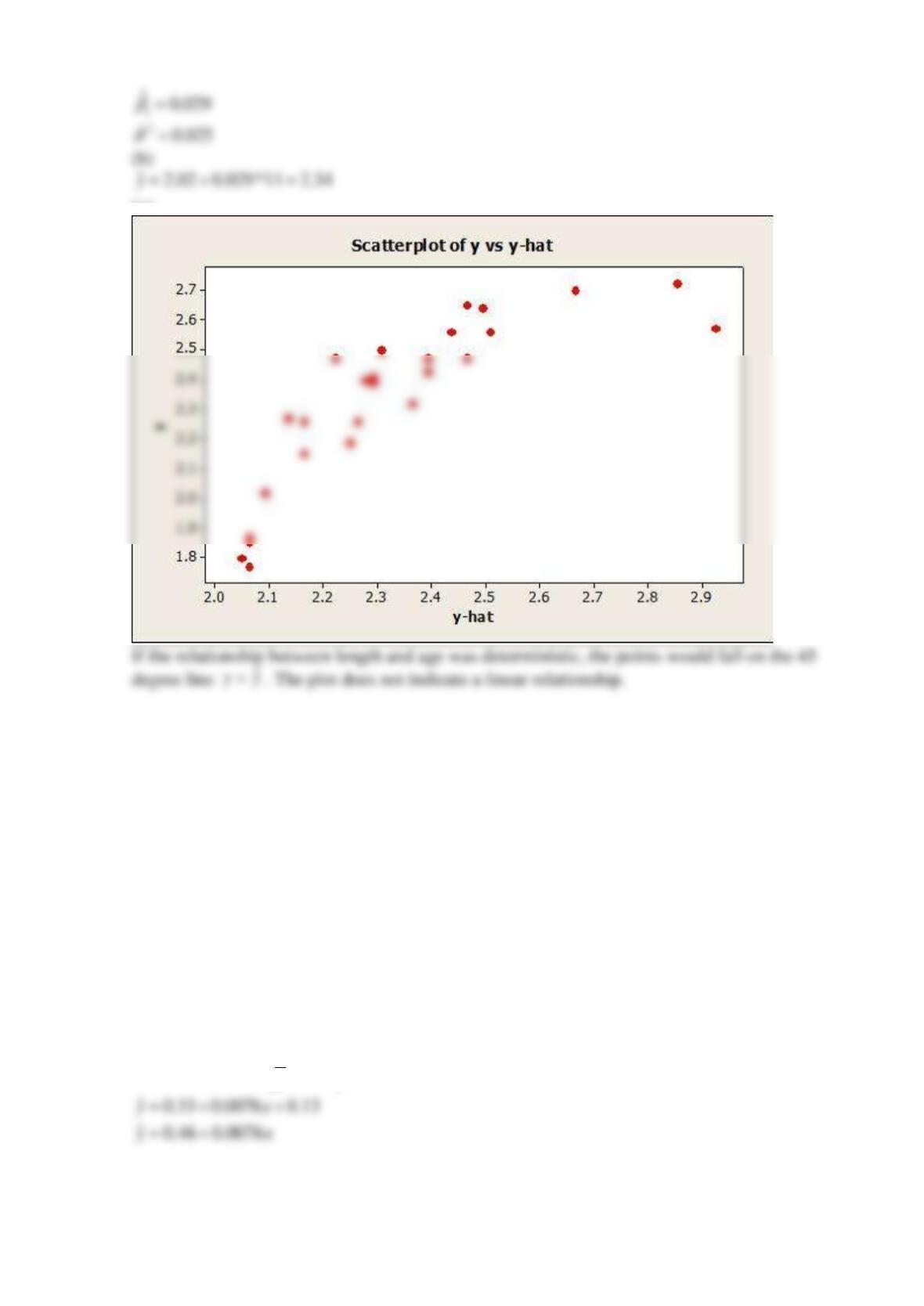
8) Because
, we reject the null hypothesis at
. We can therefore conclude
that the model specifies a useful linear relationship at
.
Reserve Problems Chapter 11 Section 4 Problem 2
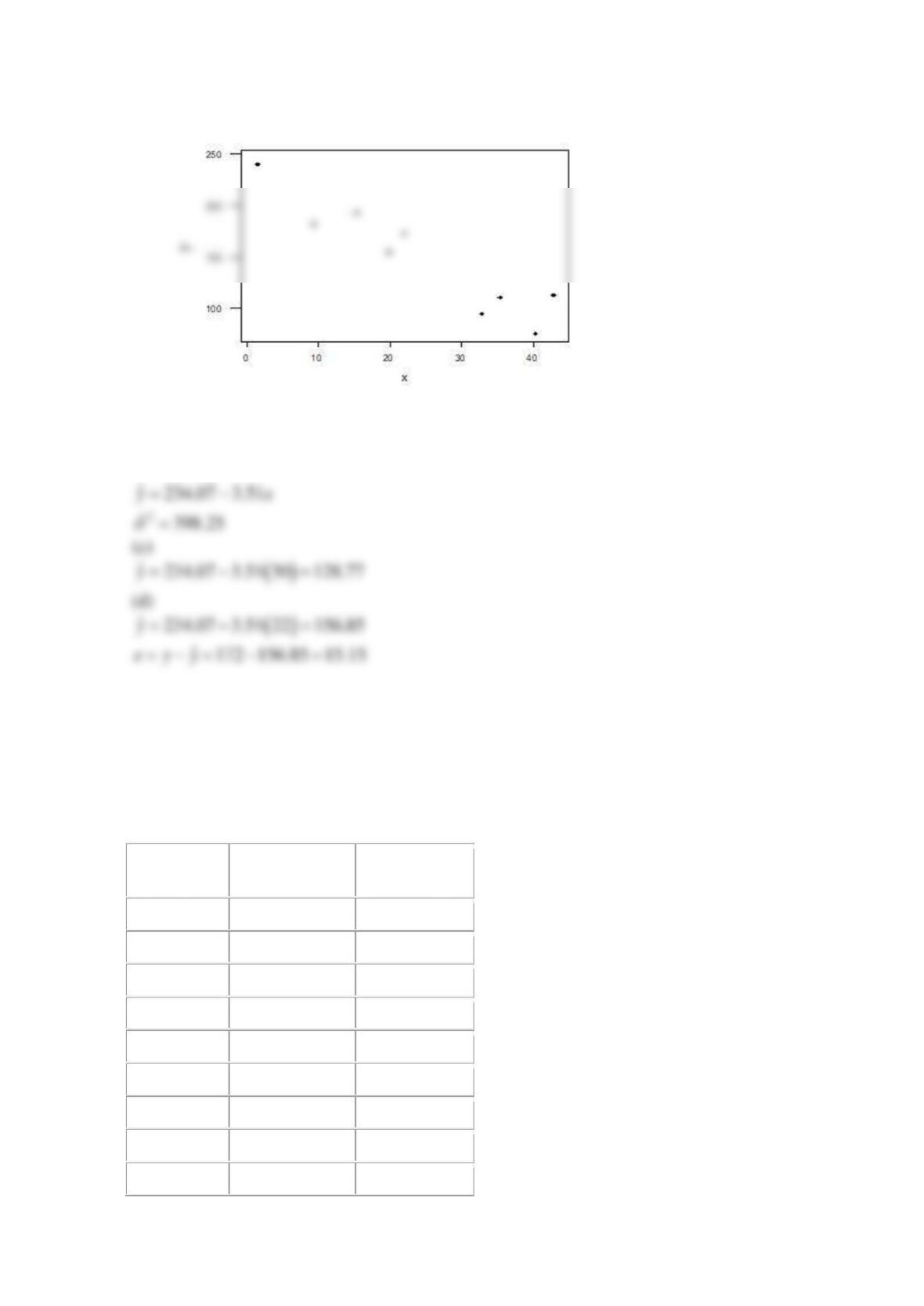
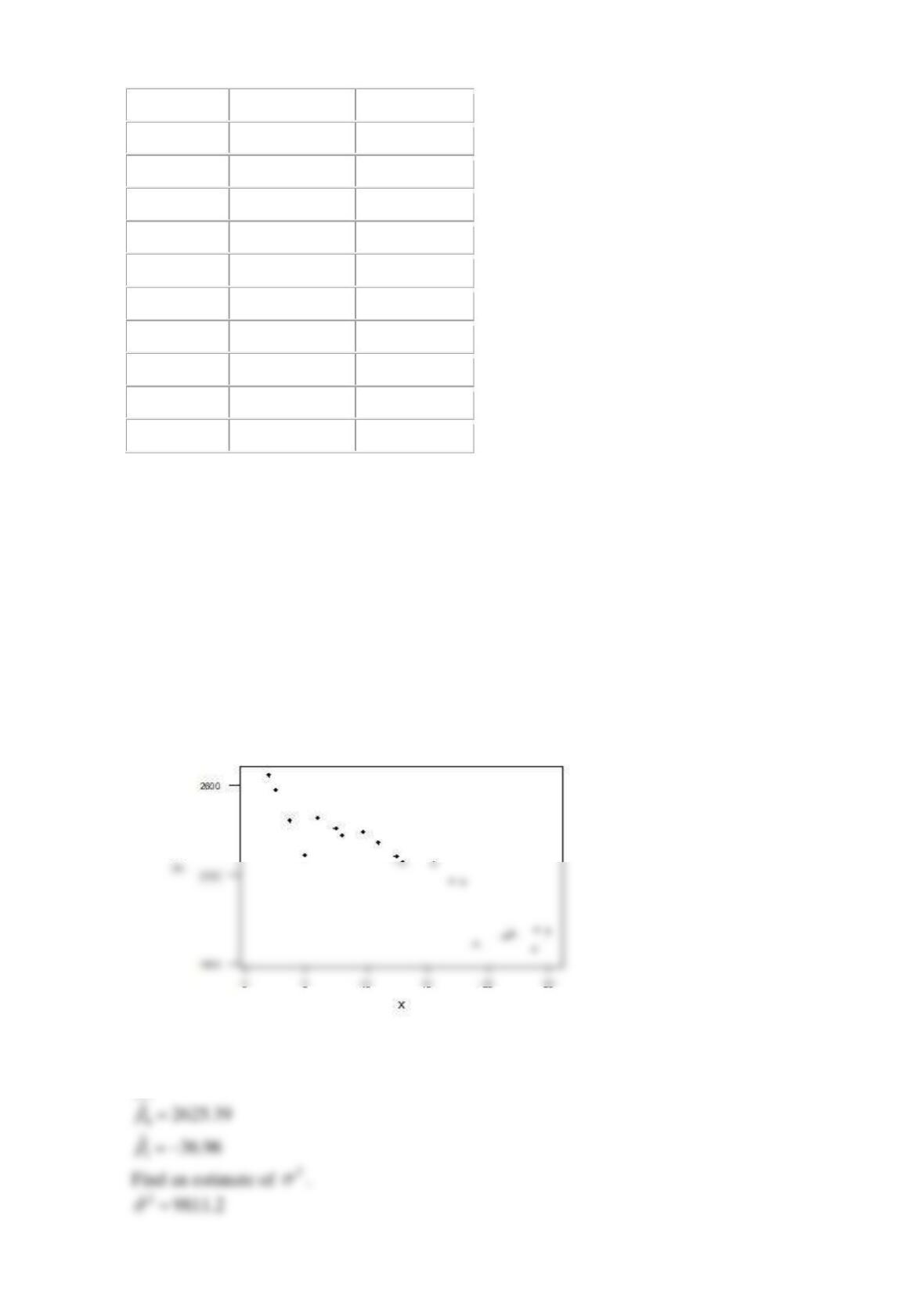
A runner was tested on a treadmill. During the test, his speed x (in km/h) and his heart rate y
were measured. The results are shown in the table.
(a) Test for the significance of regression using the analysis of variance with
. Find the
P-value for this test. Can you conclude that the model specifies a useful linear relationship
between these two variables?
(b) Estimate
.
(c) Estimate the standard error of the slope and intercept in this model.
(d) Test the hypothesis that the increase in the speed of 1 km/h results in the runner’s heart rate
average increase of 7 points at
. Suppose that the alternative hypothesis is that the
average increase of the runner’s heart rate in this situation does not equal 7 points.
SOLUTION
(a)
,
,
,
,