Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
1
Solutions To Problems of Chapter 16
16.1. Prove that an undirected graph is triangulated if and only if its cliques
can be organized into a join tree.
Solution: The proof follows [Jens 01].
a) Let the cliques be organized in a join tree. Let Vbe a leaf clique
and let Fbe its unique neighbor. From the definition of a join tree and
16.2. For the graph of Figure 16.3a give all possible perfect elimination se-
quences and draw the resulting sequence of graphs.
Solution: Alternative perfect elimination sequences are:
x5, x6, x3, x1, x2, x4,
16.3. Derive the formulas for the marginal probabilities of the variables in a) a
clique node and b) in a separator node in a junction tree.
2
(a) (b)
(c) (d) (e)
Figure 1: The resulting graphs associated with the elimination sequence:
x5, x6, x3, x1, x2, x4, for Problem 16.2.
Solution: The proof is direct consequence of the definition of messages.
Let ψV(xV) be a clique of variable (nodes) which comprises xV. Some
of them are not shared by any other clique, and some of them are. The
shared ones will appear in the separators with whom Vis connected to.
16.4. Prove that in a junction tree the joint pdf of the variables is given by (16.8).
Solution: We will show it first for a junction tree comprising two clique
3
Figure 2: The graph structures for Problem 16.4. The arrows indicate two
possible message flows (black and red) in different directions, which are required
Zψ2(xv2)µs→v2(xs).(3)
Also, from (16.7) we get
P(xs) = 1
Zµv1→s(xs)µv2→s(xs) (4)
Moreover, take into account that
Also,
P(xs) = 1
Zµv1→s(xs)µv2→s(xs)µv3→s(xs) (8)
where
µs→v1(xs) = µv3→s(xs)µv2→s(xs),(9)
16.5. Show that obtaining the marginal over a single variable is independent of
which one from the cliques/separators nodes, which contain the variable,
the marginalization is performed.
Hint: Prove it for the case of two neighboring clique nodes in the junction
tree.
Solution: We will consider that the two neighboring nodes V1,V2share
one variable x, which also comprises their common separator, as shown in
Figure 3. Assume for simplicity that V1is a leaf node, without harming
generality. We have that
P(x) = X
xV1
ψ1(xV1, x)µV2→S(x)
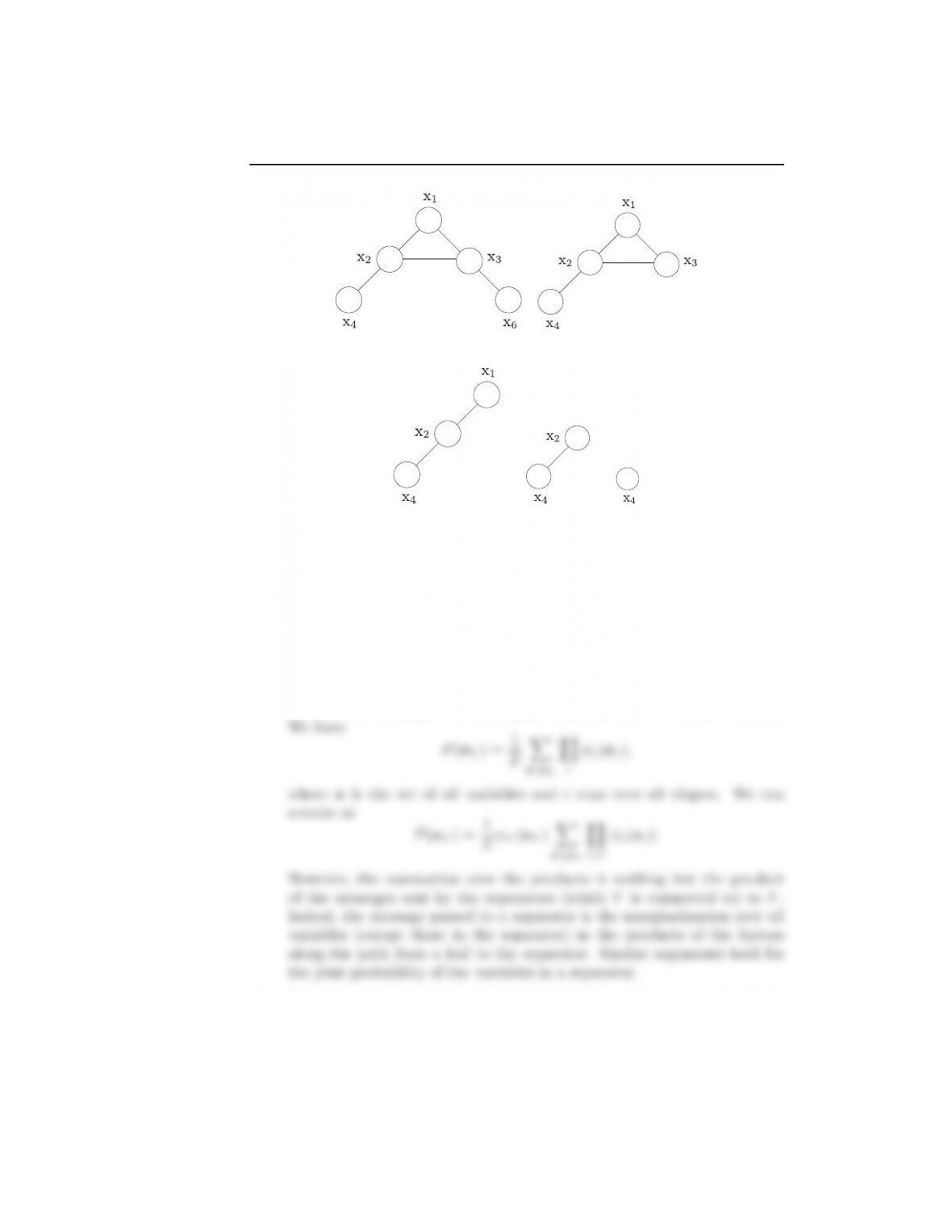
5
Figure 3: The set up for Problem 16.5
(a) (b)
Figure 4: a) The graph for the Problem 16.6. b) A triangulated graph.
16.6. Consider the graph in Figure 4a. Obtain a triangulated version of it.
16.7. Consider the Bayesian network structure given in Figure 5. Obtain a
equivalent join tree.
Solution: First, we moralize the network, and the structure of Figure
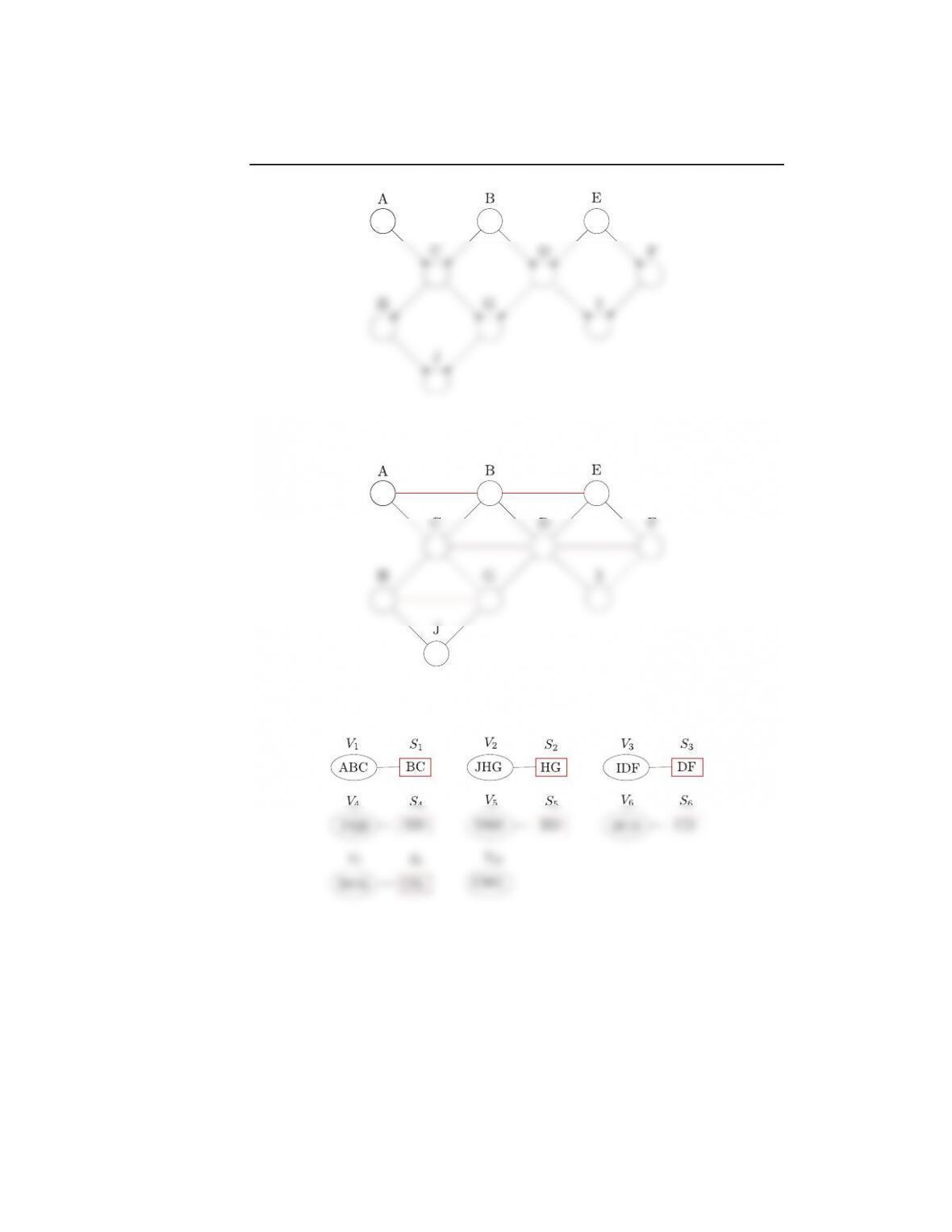
16.8. Consider the random variables A,B,C,D,E,F,G,H,I,J and assume that
the joint distribution is given by the product of the following potential
functions
p=1
Zψ1(A, B, C, D)ψ2(B, E, D)ψ3(E, D, F, I)ψ4(C, D, G)ψ5(C, H, G, J)
Construct an undirected graphical model on which the previous joint prob-
ability factorizes and in the sequence derive an equivalent junction tree.
Solution: The corresponding graph is shown in Figure 6. The nodes
are eliminated in the following sequence: F,I,H,J,G,E,D,C,B,A with
6
Figure 5: The Bayesian network structure for Problem 16.7
Figure 6: The moralized counterpart of the graph in 5
Figure 7: The set of cliques and separators after the sequence of nodes’ elimi-
nation from Figure 6.
(B, E, D), S6= (B, D), V10 = 9A, B, C, D). The resulting junction tree is
shown in Figure 10
16.9. Prove that the function
g(x) = 1 −exp(−x), x > 0,
is log-concave.
Solution: Let
16.10. Derive the conjugate function of
f(x) = ln(1 −exp(−x)).
Solution: By the definition and since f(x) is concave we have
f∗(ξ) = min
16.11. Show that minimizing the bound in Eq. (16.12) is a convex optimization
task.
Solution: Instead of minimizing the bound itself we can minimize its log-
16.12. Show that the function 1 + exp(−x), x ∈Ris log-convex and derive the
respective conjugate one.
Solution:
f(x) = ln 1 + exp(−x),
(1 + exp(−x))2
=exp(−x)
(1 + exp(−x))2>0.
16.13. Derive the KL divergence between P(Xl|X ) and Q(Xl) for the mean field
Boltzmann machine and obtain the respective variational lparameters.
Solution: The KL divergence is given by
KL =−X
Q(Xl|X ;µ) ln
exp
−X
X
θij xixj+˜
θi0xi
xi∈X l
i:xi∈X l
=X
i:xi∈X l!X
j>i
j:xj∈X l
X
xi∈X l
Q(Xl|X ;µ)θij xixj
+X
xi∈X l
Q(Xl|X ;µ)˜
θi0xi
∂KL
∂µi
=X
j6=i
θij µj+˜
θi0+ ln µi+ 1 −ln(1 −µi)−1 = 0,
or
µi=1
j6=i
16.14. Given a distribution in the exponential family,
p(x) = exp θTu(x)−A(θ),
show that A(θ) generates the respective mean parameters which define
the exponential family
∂A(θ)
∂θi
=E[ui(x)] = µi.
Also, show that A(θ) is a convex function.
Solution: By the definition of A(θ) we have
∂A(θ)
=∂
ln Zexp θTu(x)dx,
which is a nonnegative matrix. Hence convexity has been shown.
16.15. Show that the conjugate function of A(θ), associated with an exponential
distribution, such as that in Problem 16.14, is the corresponding negative
entropy function. Moreover, if µand θ(µ) are doubly coupled, then
µ=E[u(x)],
where E[·] is with respect to p(x;θ(µ)).
Solution:
A∗(µ) = max
θ θTµ−A(θ),
16.16. Derive a recursion for updating γ(xn) in HMMs independent of β(xn)
Solution: We know from the text and the respective definition that
γ(xn) = P(xn|Y) = X
xn+1
P(xn,xn+1|Y)
=X
P(xn|xn+1, Y[1:n], Y[n+1,N ])P(xn+1|Y).
16.17. Derive an efficient scheme for prediction in HMM models; that is, to ob-
tain p(yN+1|Y) where Y={y1,y2, . . . , yN}.
Solution: We have that
p(yN+1|Y) = X
xN+1
p(yN+1,xN+1|Y)
16.18. Prove the estimation formulas for the probabilities Pk,k= 1,2, . . . , K,
and Pij ,i, j = 1,2, . . . , K, in the context of the forward-backward algo-
rithm for training HMM.
Solution: From the text, we have
Q(Θ,Θ(t)) =
K
X
γ(x1,k = 1; Θ(t)) ln Pk
N
X
K
X
K
X
16.19. Consider the Gaussian Bayesian network of Section 15.3.5 defined by the
local conditional pdfs
p(xi|Pai) = N
xi|X
k:xk∈Pai
θikxk+θi0, σ2
, i = 1,2, . . . , l.
Assume a set of Nobservations, xi(n), n= 1,2, . . . , N,i= 1,2, . . . , l, and
derive a maximum likelihood estimate of the parameters θ; assume the
common variance σ2to be known.
Solution: The likelihood is given by
L(X;θ) =
N
X
n=1
l
X
i=1 −1
2σ2(xi(n)−θT
ihi(n))2,
n=1
n=1
