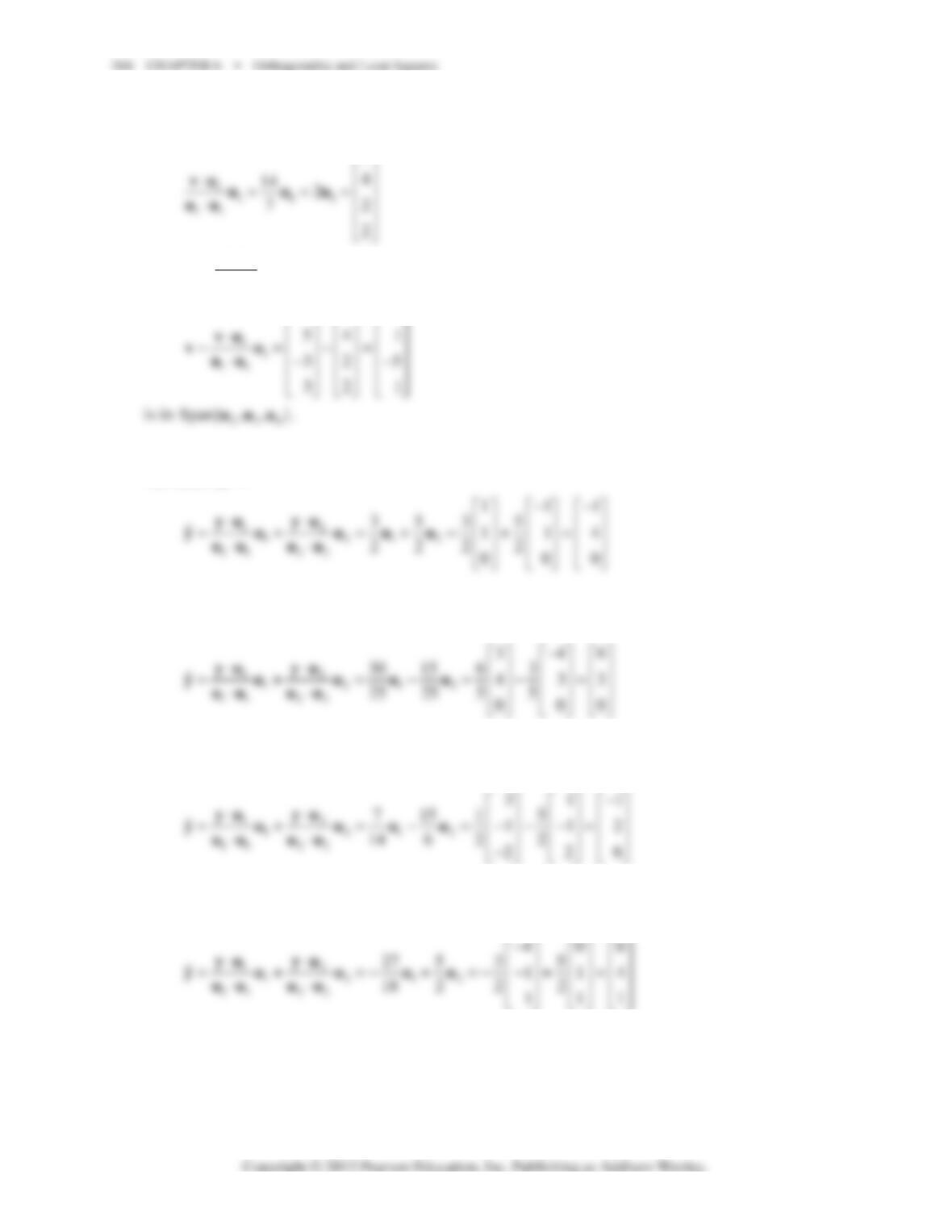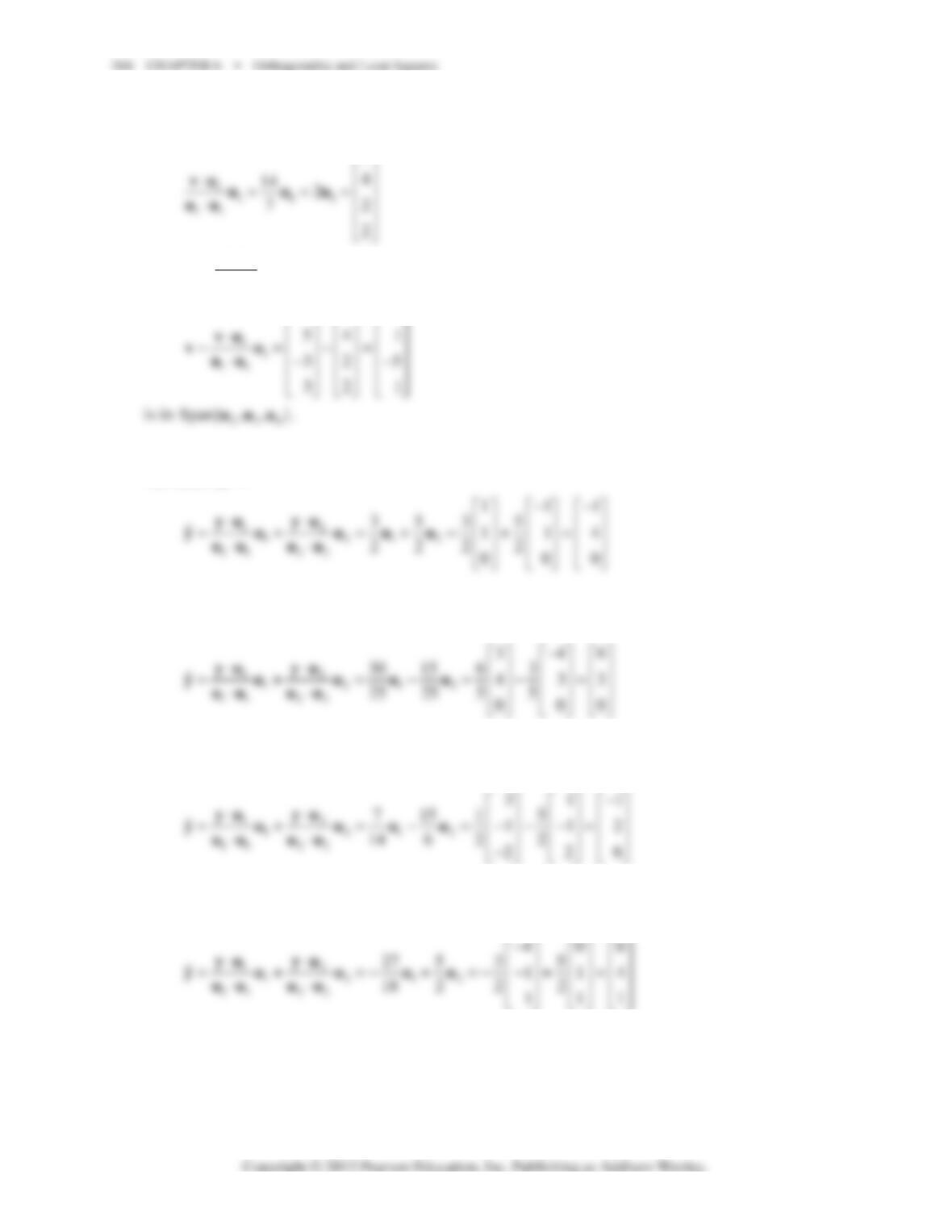r
6.1 SOLUTIONS
Notes:
The first half of this section is
c
concepts of orthogonality and orthogon
a
an important general fact, but is needed
in Section 7.4. The optional material on
1. Since 1
2
−
⎡⎤
=⎢⎥
⎣⎦
u and 4,
6
⎡⎤
=⎢⎥
⎣⎦
v
⋅
=
uu
3. Since
3
1,
5
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
−
⎣⎦
w
22
3(1)⋅= +−ww
5. Since 1
2
−
⎡⎤
=⎢⎥
⎣⎦
u and 4,
6
⎡⎤
=⎢⎥
⎣⎦
v u ⋅ v
r
c
omputational and is easily learned. The second half
c
a
l complements, which are essential for later work.
T
only for Supplementary Exercise 13 at the end of th
e
angles is not used later. Exercises 27–31 concern fact
s
22
(1) 2 5=− + =
, v ⋅ u = 4(–1) + 6(2) = 8, and
8
5
⋅=
⋅
vu
uu
2
(5) 35+− =
, and
3/35
11/35 .
1/7
⎡⎤
⎢⎥
=−
⎢⎥
⋅⎢⎥
−
⎣⎦
w
ww
= (–1)(4) + 2(6) = 8,
22
4652,⋅=+=vv and
c
oncerns the
T
heorem 3 is
e
chapter and
s
used later.
8
.
5
358 CHAPTER 6 • Orthogonality and Least Squares
6. Since
6
2
3
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
⎣⎦
x
and
3
1,
5
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
−
⎣⎦
w
x ⋅ w = 6(3) + (–2)(–1) + 3(–5) = 5,
222
6(2)349,⋅= +− + =xx
and
7. Since
3
1,
5
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
−
⎣⎦
w
222
|| || 3 ( 1) ( 5) 35.=⋅= +−+−=www
9. A unit vector in the direction of the given vector is
⎢
⎣
30 30 3/ 5
11
−−−
⎡
⎤⎡⎤⎡⎤
10. A unit vector in the direction of the given vector is
⎢
⎢
⎢
⎣
6/ 61
66
11
⎡
⎤
−
−−
⎡⎤ ⎡⎤
⎢
⎥
11. A unit vector in the direction of the given vector is
⎢
⎢
⎢
7/ 69
7/4 7/4
⎡
⎤
⎡⎤ ⎡⎤
⎢
⎥
⎣
⎦
12. A unit vector in the direction of the given vector is
22
8/3 8/3 4/5
11
223/5
100 / 9
(8 / 3) 2
⎡⎤ ⎡⎤⎡⎤
==
⎢⎥ ⎢⎥⎢⎥
⎣⎦ ⎣⎦⎣⎦
+
6.1 • Solutions 359
14. Since
0
5
2
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
⎣⎦
u
and
4
1,
8
−
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
⎣⎦
z
22 22
|| || [0 (4)] [5 (1)] [2 8] 68− = −− +− −− + − =uz
and
18. Since y ⋅ z = (–3)(1) + 7(–8) + 4(15) + 0(–7) = 1 ≠ 0, y and z are not orthogonal.
19. a. True. See the definition of || v ||.
b . True. See Theorem 1(c).
c . True. See the discussion of Figure 5.
20. a. True. See Example 1 and Theorem 1(a).
b . False. The absolute value sign is missing. See the box before Example 2.
21. Theorem 1(b):
() () ( )
TTTTT
+ ⋅ = + = + = + =⋅ +⋅uvw uvw u vwuwvwuwvw
The second and third equalities used Theorems 3(b) and 2(c), respectively, from Section 2.1.
22. Since u ⋅ u is the sum of the squares of the entries in u, u ⋅ u ≥ 0. The sum of squares of numbers is
zero if and only if all the numbers are themselves zero.
24. One computes that
222
|| || ( ) ( ) 2 || || 2 || ||+=+⋅+=⋅+⋅+⋅= +⋅+uv uv uv uu uvvv u uv v
and
360 CHAPTER 6 • Orthogonality and Least Squares
25. When
,
a
b
⎡⎤
=⎢⎥
⎣⎦
v the set H of all vectors x
y
⎡
⎤
⎢
⎥
⎣
⎦
that are orthogonal to v is the subspace of vectors whose
entries satisfy ax + by = 0. If a ≠ 0, then x = – (b/a)y with y a free variable, and H is a line through
the origin. A natural choice for a basis for H in this case is
.
b
a
⎧
⎫−
⎡
⎤
⎪
⎪
⎨
⎬
⎢
⎥
⎪
⎣
⎧
⎡
⎪
⎨
⎢
⎪
⎣
⎧
⎡
⎪
⎨
⎢
⎪
⎣
If a = 0 and b ≠ 0, then by = 0.
26. Theorem 2 in Chapter 4 may be used to show that W is a subspace of
3
, because W is the null space
of the 1 × 3 matrix
.
T
u
Geometrically, W is a plane through the origin.
27. If y is orthogonal to u and v, then y ⋅ u = y ⋅ v = 0, and hence by a property of the inner product,
y ⋅ (u + v) = y ⋅ u + y ⋅ v = 0 + 0 = 0. Thus y is orthogonal to u + v.
28. An arbitrary w in Span{u, v} has the form
12
cc=+wuv
. If y is orthogonal to u and v, then
u ⋅ y = v ⋅ y = 0. By Theorem 1(b) and 1(c),
30. a. If z is in
,
W
⊥
u is in W, and c is any scalar, then (cz) ⋅ u = c(z ⋅ u) = c
0 = 0. Since u is any
element of W, c
z is in
.W⊥
31. Suppose that x is in W and
.W⊥
Since x is in
,
W
⊥
x is orthogonal to every vector in W, including x
itself. So x ⋅ x = 0, which happens only when x = 0.
32. [M]
a. One computes that
1234
|| || || || || || || || 1====aa aa
and that
0
ij
⋅=aa
for i ≠ j.
33. [M] Answers to the calculations will vary, but will demonstrate that the mapping
()T⋅
⎛⎞
=⎜⎟
⋅
⎝⎠
xv
xx v
vv
(for v ≠ 0) is a linear transformation. To confirm this, let x and y be in
n
, and
34. [M] One finds that
51
1050 1/3
14
−
⎡⎤
⎢⎥ −
−⎡⎤
6.2 SOLUTIONS
Notes:
The nonsquare matrices in Theorems 6 and 7 are needed for the QR factorization in Section 6.4. It
is important to emphasize that the term orthogonal matrix applies only to certain square matrices. The
subsection on orthogonal projections not only sets the stage for the general case in Section 6.3, it also
provides what is needed for the orthogonal diagonalization exercises in Section 7.1, because none of the
eigenspaces there have dimension greater than 2. For this reason, the Gram-Schmidt process (Section 6.4)
is not really needed in Chapter 7. Exercises 13 and 14 are good preparation for Section 6.3.
1. Since
13
4420,
−
⎡⎤⎡⎤
⎢⎥⎢⎥
⋅− = ≠
⎢⎥⎢⎥
the set is not orthogonal.
362 CHAPTER 6 • Orthogonality and Least Squares
10 1 5 0 5
−−
⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤
3. Since
63
31300,
91
−
⎡⎤⎡⎤
⎢⎥⎢⎥
−⋅ =− ≠
⎢⎥⎢⎥
⎢⎥⎢⎥
−
⎣⎦⎣⎦
the set is not orthogonal.
20 2 4 0 4
⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤
31 33 13
−−
⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤
6. Since
43
1332 0,
35
81
−
⎡⎤⎡⎤
⎢⎥⎢⎥
⎢⎥⎢⎥
⋅=−≠
⎢⎥⎢⎥
−
⎢⎥⎢⎥
−
⎢⎥⎢⎥
⎣⎦⎣⎦
the set is not orthogonal.
7. Since
12
12 12 0,⋅=−=uu
12
{, }uu
is an orthogonal set. Since the vectors are non-zero,
1
u
and
2
u
are linearly independent by Theorem 4. Two such vectors in
2
automatically form a basis for
2
. So
12
{, }uu
is an orthogonal basis for
2
. By Theorem 5,
8. Since
12 660,⋅=−+=uu
12
{, }uu
is an orthogonal set. Since the vectors are non-zero,
1
u
and
2
u
are linearly independent by Theorem 4. Two such vectors in
2
automatically form a basis for
2
. So
12
{, }uu
is an orthogonal basis for
2
. By Theorem 5,
9. Since
12 13 23
0,⋅=⋅=⋅=uu uu u u
,
123
{, }uuu
is an orthogonal set. Since the vectors are non-zero,
1,u
2,u
and
3
u
are linearly independent by Theorem 4. Three such vectors in
3
automatically form
6.2 • Solutions 363
10. Since
12 13 23
0,⋅=⋅=⋅=uu uu u u
,
123
{, }uuu
is an orthogonal set. Since the vectors are non-zero,
1,u
2,u
and
3
u
are linearly independent by Theorem 4. Three such vectors in
3
automatically form
11. Let
1
7
⎡⎤
=⎢⎥
⎣⎦
y and
4.
2
−
⎡
⎤
=
⎢
⎥
⎣
⎦
u The orthogonal projection of y onto the line through u and the origin is
the orthogonal projection of y onto u, and this vector is
12. Let
1
1
⎡⎤
=⎢⎥
−
⎣⎦
y and
1.
3
−
⎡
⎤
=
⎢
⎥
⎣
⎦
u The orthogonal projection of y onto the line through u and the origin is
13. The orthogonal projection of y onto u is
4/5
13
ˆ7/5
65
−
⎡⎤
⋅
==−=
⎢⎥
⋅⎣⎦
yu
yuu
uu
⎡
⎢
⎣
14. The orthogonal projection of y onto u is
14 / 5
2
ˆ2/5
5
⎡⎤
⋅
===
⎢⎥
⋅⎣⎦
yu
yuu
uu
⎡
⎢
⎣
15. The distance from y to the line through u and the origin is ||y –
ˆ
y
||. One computes that
383/5
3
ˆ164/5
10
⎡⎤ ⎡⎤ ⎡ ⎤
⋅
−=− = − =
⎢⎥ ⎢⎥ ⎢ ⎥
−
⋅⎣⎦ ⎣⎦ ⎣ ⎦
yu
yyy u
uu
364 CHAPTER 6 • Orthogonality and Least Squares
16. The distance from y to the line through u and the origin is ||y –
ˆ
y
||. One computes that
17. Let
1/3
1/3 ,
1/3
⎡⎤
⎢⎥
=⎢⎥
⎢⎥
⎣⎦
u
1/2
0.
1/2
−
⎡⎤
⎢⎥
=⎢⎥
⎢⎥
⎣⎦
v
Since u ⋅ v = 0, {u, v} is an orthogonal set. However,
2
|| || 1/ 3=⋅=uuu
and
2
|| || 1/ 2,=⋅=vvv
so {u, v} is not an orthonormal set. The vectors u and v may be normalized to
18. Let
0
1,
0
⎡⎤
⎢⎥
=⎢⎥
⎢⎥
⎣⎦
u
0
1.
0
⎡⎤
⎢⎥
=−
⎢⎥
⎢⎥
⎣⎦
v
Since u ⋅ v = –1 ≠ 0, {u, v} is not an orthogonal set.
19. Let
.6 ,
.8
−
⎡⎤
=⎢⎥
⎣⎦
u
.8 .
.6
⎡⎤
=⎢⎥
⎣⎦
v
Since u ⋅ v = 0, {u, v} is an orthogonal set. Also,
2
|| || 1=⋅=uuu
and
20. Let
2/3
1/3 ,
2/3
−
⎡⎤
⎢⎥
=⎢⎥
⎢⎥
⎣⎦
u
1/3
2/3 .
0
⎡
⎤
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
v
Since u ⋅ v = 0, {u, v} is an orthogonal set. However,
2
|| || 1=⋅=uuu
21. Let
1/ 10
3/ 20 ,
⎢
⎢
⎣
⎢
⎣
⎡⎤
⎢⎥
=
⎢⎥
u
3/ 10
1/ 20 ,
⎡
⎤
⎢
⎥
=−
⎢
⎥
v and
0
1/ 2 .
⎡
⎤
⎢
⎥
=−
⎢
⎥
w Since u ⋅ v = u ⋅ w = v ⋅ w = 0, {u, v, w} is an
6.2 • Solutions 365
22. Let
1/ 18
4/ 18 ,
⎢
⎣
⎢
⎣
⎡⎤
⎢⎥
=
⎢⎥
u
1/ 2
0,
⎡
⎤
⎢
⎥
=
⎢
⎥
v and
2/3
1/3 .
−
⎡
⎤
⎢
⎥
=
⎢
⎥
w Since u ⋅ v = u ⋅ w = v ⋅ w = 0, {u, v, w} is an
23. a. True. For example, the vectors u and y in Example 3 are linearly independent but not orthogonal.
b . True. The formulas for the weights are given in Theorem 5.
24. a. True. But every orthogonal set of nonzero vectors is linearly independent. See Theorem 4.
b . False. To be orthonormal, the vectors is S must be unit vectors as well as being orthogonal to each
25. To prove part (b), note that
()( )()( )
TTTT
UU UU UU⋅= = ==⋅xy xyx yxyxy
26. A set of n nonzero orthogonal vectors must be linearly independent by Theorem 4, so if such a set
spans W it is a basis for W. Thus W is an n–dimensional subspace of
n
, and
W=
n
.
27. If U has orthonormal columns, then
T
UU I=
by Theorem 6. If U is also a square matrix, then the
28. If U is an n × n orthogonal matrix, then
1T
IUU UU
−
==
. Since U is the transpose of
,
T
U Theorem
29. Since U and V are orthogonal, each is invertible. By Theorem 6 in Section 2.2, UV is invertible and
30. If U is an orthogonal matrix, its columns are orthonormal. Interchanging the columns does not
change their orthonormality, so the new matrix – say, V – still has orthonormal columns. By
31. Suppose that
ˆ.
⋅
=⋅
yu
yu
uu
Replacing u by cu with c ≠ 0 gives
32. If
12
0⋅=
vv , then by Theorem 1(c) in Section 6.1,
33. Let L = Span{u}, where u is nonzero, and let
()T
⋅
=⋅
xu
xu
uu
. For any vectors x and y in
n
and any
scalars c and d, the properties of the inner product (Theorem 1) show that
()
()
cd
Tc d
+⋅
+= ⋅
xyu
xy u
uu
cd
⋅+ ⋅
=⋅
xu yu
u
uu
34. Let L = Span{u}, where u is nonzero, and let
( ) refl 2proj
LL
T== −
xy yy
. By Exercise 33, the
mapping
projL
yy
is linear. Thus for any vectors y and z in
n
and any scalars c and d,
()2proj()()
L
Tc d c d c d+= +−+
yz yz yz
2( proj proj )
LL
cd cd=+−−
yzyz
35. [M] One can compute that
4
100 .
T
AA I=
Since the off-diagonal entries in
T
AA are zero, the columns
of A are orthogonal.
36. [M]
a. One computes that
4
,
T
UU I=
while
82 020 8 62024 0
04224 020 62032
20 24 58 20 0 32 0 6
−
⎡⎤
⎢⎥
−−
⎢⎥
⎢⎥
−
The matrices
T
UU
and
T
UU
are of different sizes and look nothing like each other.
b. Answers will vary. The vector
T
UU=py
is in Col
U because
()
T
UU=py
. Since the columns of
U are simply scaled versions of the columns of A, Col
U = Col
A. Thus each p is in Col A.
6.3 SOLUTIONS
Notes:
Example 1 seems to help students understand Theorem 8. Theorem 8 is needed for the Gram-
Schmidt process (but only for a subspace that itself has an orthogonal basis). Theorems 8 and 9 are
needed for the discussions of least squares in Sections 6.5 and 6.6. Theorem 10 is used with the QR
factorization to provide a good numerical method for solving least squares problems, in Section 6.5.
Exercises 19 and 20 lead naturally into consideration of the Gram-Schmidt process.
1. The vector in
4
Span{ }
u is
10
⎡⎤
Since
4
11 2 2 3 3 4
44
,cc c ⋅
=+ + +
⋅
xu
xu u u u
uu the vector
⎢
⎢
⎢
⎢
⎢
⎣
10 10 0
⎡
⎤⎡ ⎤⎡ ⎤
2. The vector in
1
Span{ }
u is
2
⎡⎤
Since
11223344
11
,ccc
⋅
=+++
⋅
vu
x uuuu
uu the vector
⎢
⎢
⎢
⎢
⎢
⎣
42 2
⎡
⎤⎡⎤⎡ ⎤
3. Since
12 110 0,⋅=−++=
uu
12
{, }
uu is an orthogonal set. The orthogonal projection of y onto
12
Span{ , }
uu is
⎡
⎢
⎢
⎢
⎣
4. Since
12 12 12 0 0,⋅=−++=
uu
12
{, }
uu is an orthogonal set. The orthogonal projection of y onto
12
Span{ , }
uu is
⎡
⎢
⎢
⎢
⎣
5. Since
12
314 0,⋅=+−=
uu
12
{, }
uu is an orthogonal set. The orthogonal projection of y onto
12
Span{ , }
uu is
⎡
⎢
⎢
⎢
⎣
6. Since
120110,⋅=−+=
uu
12
{, }
uu is an orthogonal set. The orthogonal projection of y onto
12
Span{ , }
uu is
⎡
⎢
⎢
⎢
⎣
7. Since
12
5380,⋅=+−=
uu
12
{, }
uu is an orthogonal set. By the Orthogonal Decomposition
Theorem,
6.3 • Solutions 369
⎡
⎢
⎢
⎢
⎣
8. Since
12 132 0,⋅=−+−=
uu
12
{, }
uu is an orthogonal set. By the Orthogonal Decomposition
Theorem,
⎢
⎢
⎢
⎣
3/2 5/2
−
⎡
⎤⎡⎤
9. Since
12 13 23
0,⋅=⋅=⋅=
uu uu u u
123
{, , }
uu u is an orthogonal set. By the Orthogonal
Decomposition Theorem,
⎢
⎢
⎢
⎢
⎢
⎣
22
⎡
⎤⎡⎤
10. Since
12 13 23
0,⋅=⋅=⋅=
uu uu u u
123
{, , }
uu u is an orthogonal set. By the Orthogonal
Decomposition Theorem,
⎢
⎢
⎢
⎢
⎢
⎣
52
−
⎡
⎤⎡⎤
11. Note that
1
v and
2
v are orthogonal. The Best Approximation Theorem says that
ˆ
y, which is the
orthogonal projection of y onto
12
Span{ , },W=
vv is the closest point to y in W. This vector is
⎢
⎢
⎢
⎢
⎢
⎣
3
⎡
⎤
12. Note that
1
v and
2
v are orthogonal. The Best Approximation Theorem says that
ˆ
y, which is the
orthogonal projection of y onto
12
Span{ , },W=
vv is the closest point to y in W. This vector is
370 CHAPTER 6 • Orthogonality and Least Squares
⎡
⎢
⎢
⎢
⎢
⎢
⎣
13. Note that
1
v and
2
v are orthogonal. By the Best Approximation Theorem, the closest point in
12
Span{ , }
vv to z is
⎢
⎢
⎢
⎢
⎢
⎣
1
−
⎡
⎤
14. Note that
1
v and
2
v are orthogonal. By the Best Approximation Theorem, the closest point in
12
Span{ , }
vv to z is
⎢
⎢
⎢
⎢
⎢
⎣
1
⎡
⎤
15. The distance from the point y in
3
to a subspace W is defined as the distance from y to the closest
point in W. Since the closest point in W to y is
ˆproj ,
W
=
yy
the desired distance is || y –
ˆ
y||. One
16. The distance from the point y in
4
to a subspace W is defined as the distance from y to the closest
point in W. Since the closest point in W to y is
ˆproj ,
W
=
yy
the desired distance is || y –
ˆ
y||. One
−1 4
⎡⎤ ⎡⎤
17. a.
8/9 2/9 2/9
10
, 2/9 5/9 4/9
01 2/9 4/9 5/9
TT
UU UU
−
⎡⎤
⎡⎤ ⎢⎥
==−
⎢⎥ ⎢⎥
⎣⎦ ⎢⎥
⎣⎦
b . Since
2
,
T
UU I=
the columns of U form an orthonormal basis for W, and by Theorem 10
6.3 • Solutions 371
18. a.
[]
1/10 3/10
11, 3/10 9/10
TT
UU UU
−
⎡⎤
== =
⎢⎥
−
⎣⎦
19. By the Orthogonal Decomposition Theorem,
3
u is the sum of a vector in
12
Span{ , }W=
uu and a
vector v orthogonal to W. This exercise asks for the vector v:
⎢
⎢
⎢
⎣
000
⎡
⎤⎡ ⎤⎡ ⎤
20. By the Orthogonal Decomposition Theorem,
4
u is the sum of a vector in
12
Span{ , }W=
uu and a
vector v orthogonal to W. This exercise asks for the vector v:
⎢
⎢
⎢
⎣
000
⎡
⎤⎡ ⎤⎡ ⎤
21. a. True. See the calculations for
2
z in Example 1 or the box after Example 6 in Section 6.1.
b . True. See the Orthogonal Decomposition Theorem.
22. a. True. See the proof of the Orthogonal Decomposition Theorem.
b . True. See the subsection “A Geometric Interpretation of the Orthogonal Projection.”
23. By the Orthogonal Decomposition Theorem, each x in
n
can be written uniquely as x = p + u, with
p in Row A and u in
(Row ) .A
⊥
By Theorem 3 in Section 6.1,
(Row ) Nul ,AA
⊥
=
so u is in Nul
A.
24. a. By hypothesis, the vectors
1
w, …,
p
w
are pairwise orthogonal, and the vectors
1
v, …,
q
v
are
pairwise orthogonal. Since
i
w is in W for any i and
j
v
is in
W⊥
for any j,
0
ij
⋅=wv
for any i
and j. Thus
11
{,, ,,,}
pq
……wwvv
forms an orthogonal set.
25. [M] Since
4
T
UU I=
, U has orthonormal columns by Theorem 6 in Section 6.2. The closest point to
y in Col U is the orthogonal projection
ˆ
y of y onto Col U. From Theorem 10,
1.2
⎡⎤
⎢⎥
.4
26. [M] The distance from b to Col
U is || b –
ˆ
b||, where
ˆ.UU Τ
=
bb One computes that
.2 .8
⎡⎤ ⎡⎤
⎢⎥ ⎢⎥
.92 .08
⎢⎥ ⎢⎥
⎢⎥ ⎢⎥
.44 .56
6.4 • Solutions 373
6.4 SOLUTIONS
Notes:
The QR factorization encapsulates the essential outcome of the Gram-Schmidt process, just as the
LU factorization describes the result of a row reduction process. For practical use of linear algebra, the
factorizations are more important than the algorithms that produce them. In fact, the Gram-Schmidt
process is not the appropriate way to compute the QR factorization. For that reason, one should consider
deemphasizing the hand calculation of the Gram-Schmidt process, even though it provides easy exam
1. Set
11
=
vx
and compute that
21
22 12 1
11
1
35.
3
−
⎡
⎤
⋅
⎢
⎥
=− =− =
⎢
⎥
⋅
⎢
⎥
−
⎣
xv
vx vx v
vv Thus an orthogonal basis for W
2. Set
11
=
vx
and compute that
21
22 12 1
11
5
14.
28
⎡
⎤
⋅
⎢
⎥
=− =− =
⎢
⎥
⋅
⎢
⎥
−
⎣
⎦
xv
vx vx v
vv Thus an orthogonal basis for W
3. Set
11
=
vx
and compute that
21
22 12 1
11
3
13/2 .
23/2
⎡
⎤
⋅
⎢
⎥
=− =− =
⎢
⎥
⋅
⎢
⎥
⎣
⎦
xv
vx vx v
vv Thus an orthogonal basis for
4. Set
11
=
vx
and compute that
21
22 12 1
11
3
(2) 6.
3
⎡
⎤
⋅
⎢
⎥
=− =−− =
⎢
⎥
⋅
⎢
⎥
⎣
xv
vx vx v
vv Thus an orthogonal basis for
374 CHAPTER 6 • Orthogonality and Least Squares
5. Set
11
=
vx
and compute that
21
22 12 1
11
5
1
2.
4
⎢
⎣
⎡
⎤
⎢
⎥
⋅
⎢
⎥
=− =− =
⎢
⎥
−
⋅
⎢
⎥
xv
vx vx v
vv Thus an orthogonal basis for W
6. Set
11
=
vx
and compute that
21
22 12 1
11
4
6
(3) .
3
⎢
⎢
⎣
⎡
⎤
⎢
⎥
⋅
⎢
⎥
=− =−− =
⎢
⎥
−
⋅
xv
vx vx v
vv Thus an orthogonal basis for
7. Since
1
|| || 30=v
and
2
|| || 27/ 2 3 6 / 2,==v
an orthonormal basis for W is
2/ 30 2/ 6
⎧⎫
⎡⎤⎡⎤
8. Since
1
|| || 50=v
and
2
|| || 54 3 6,==v
an orthonormal basis for W is
3/ 50 1/ 6
⎧⎫
⎡⎤⎡⎤
9. Call the columns of the matrix
1
x,
2
x, and
3
x and perform the Gram-Schmidt process on these
vectors:
⎡
⎢
⎢
⎢
⎢
⎢
⎣
6.4 • Solutions 375
31 32
33 1 23 1 2
11 2 2
3
1
31
1
22
3
−
⎡
⎤
⎢
⎥
⋅⋅ ⎛⎞
⎢
⎥
=− − =− −− =
⎜⎟
⎢
⎥
⋅⋅ ⎝⎠
⎢
⎥
⎢
⎥
⎣
⎦
xv xv
vx v vx v v
vv v v
10. Call the columns of the matrix
1
x,
2
x, and
3
x and perform the Gram-Schmidt process on these
vectors:
11
=
vx
⎡
⎢
⎢
⎢
⎢
⎢
⎣
31 32
33 1 23 1 2
11 2 2
1
1
15
3
22
1
−
⎡
⎤
⎢
⎥
−
⋅⋅
⎢
⎥
=− − =− − =
⎢
⎥
⋅⋅
⎢
⎥
−
⎢
⎥
⎣
⎦
xv xv
vx v vx v v
vv vv
131
⎧⎫−−
⎡⎤⎡⎤⎡⎤
11. Call the columns of the matrix
1
x,
2
x, and
3
x and perform the Gram-Schmidt process on these
vectors:
11
=
vx
⎢
⎢
⎢
⎢
⎢
⎣
3
0
⎡
⎤
⎢
⎥
⎢
⎢
⎢
⎢
⎢
⎣
2
0
⎡
⎤
⎢
⎥
376 CHAPTER 6 • Orthogonality and Least Squares
132
⎧⎫
⎡⎤⎡⎤⎡⎤
12. Call the columns of the matrix
1
x,
2
x, and
3
x and perform the Gram-Schmidt process on these
vectors:
11
=
vx
1
−
⎡⎤
⎢
⎢
⎢
⎢
⎢
⎣
3
3
⎡
⎤
⎢
⎥
Thus an orthogonal basis for W is
113
113
,, .
020
⎧⎫
−
⎡⎤⎡⎤⎡⎤
⎪⎪
⎢⎥⎢⎥⎢⎥
−
⎪⎪
⎢⎥⎢⎥⎢⎥
⎪⎪
⎢⎥⎢⎥⎢⎥
13. Since A and Q are given,
59
⎡⎤
⎢⎥
14. Since A and Q are given,
23
−
⎡⎤
⎢⎥
15. The columns of Q will be normalized versions of the vectors
1
v,
2
v, and
3
v found in Exercise 11.
Thus