Exercise 1
Construction Math
OBJECTIVE
The objective of this exercise is to properly perform
construction-related math equations.
TEXTBOOK REFERENCE
Information related to this activity can be found in the
Landscape Construction textbook in Chapter 4, Construc-
tion Math.
INTRODUCTION
Whether counting the number of shrubs needed for a
planting bed or determining how much concrete to order,
is essential when working on a project, as contractors
typically build upon primary calculations to determine
subsequent numerical values.
The basic math functions covered by this lab manual
include performing item counts, calculating averages,
making linear measurements, and calculating perim-
eters, areas, volumes, and weights. It is assumed that
the reader has already mastered basic math calculations
such as addition, subtraction, multiplication, and divi-
sion of whole numbers, fractions, and decimals. For the
reader’s reference, a written description of geometric
shapes is provided in Table 1–1, and formulas for use in
perimeter, area, and volume calculations are featured in
Figures 1–2, 1–5, and 1–6.
Table 1–1 Common geometric shapes.
• Square/rectangle/parallelogram: Shapes with
two sets of parallel sides. Squares and rectangles
have right-angled corners and parallelograms have
no right-angled corners.
• Trapezoid: Shape with four sides, but only one set of
parallel sides.
• Circle: Round shape with edges equidistant from center.
• Circle sectors: Partial segments of a circle. Defined
by length of the outside arc or the enclosed angle of a
circle measured in degrees.
• Ellipse: Rounded egg shape with edges at variable
distances from center.
97171_01_ch01_p001-010.indd 1 14/06/10 8:38 PM
count, use a plan or installed design to count how many
of a particular object are used in a project. Performing
item counts for bids, estimates, and material ordering
may require separating items into groups of materials
that are the same.
Averages
Averages are used when the contractor needs to calculate
one typical, or average, number from several different
where n equals the number of numbers.
When performing landscape calculations:
• Decimals should not be rounded any smaller
than hundredths (two places).
• Fraction additions require determining the
lowest common denominator.
Linear Measurements
A foundational measurement used in landscape con-
tracting is the linear measurement, or length, of a particu-
lar distance or the dimensions of an object. Items such as
Direct Measurement. Direct measurement involves the
use of a tape measure, measuring wheel, or other measur–
ing device to determine the distance between two points.
To direct measure:
• On flat surfaces, stretch or run the measuring
device between the two points to be measured and
record the distance.
• On sloped surfaces, extend a tape measure
from the highest point along the distance being
method will give an accurate measurement of the
horizontal distance between the two points along
the slope, not the diagonal distance.) (Figure 1–1.)
Pacing. The pacing method of measurement uses an
individual’s typical step to determine distances.
To measure by pacing:
• Determine the average length of your pace. To
do this, set up a course that is a known distance
(e.g., 100 feet), and pace the course three times,
counting the number of steps required to walk
the length of the course. Calculate your average
number of steps. Divide the distance by the
2 Exercise 1 Construction Math
0′ on tape
0′ on tape
Level tape
Level tape
Plumb bob
Plumb bob
Read measurements
Add measurements together
97171_01_ch01_p001-010.indd 2 14/06/10 8:38 PM
pacing practice until you are routinely within
5 percent of an actual, measured distance.
Estimation. Estimating requires determining a distance
based on comparison with a known dimension. When
accuracy is not critical, estimating linear dimensions is a
viable option.
Estimation can be performed by:
• Comparison. This requires visually comparing the
distance to be measured to an object with known
measurements. Items such as door openings
(usually 7 feet high), and sidewalk squares can be
Perimeter Measurements
Perimeter calculations determine the total linear mea-
surement of the outside edges of an area or object. Perim-
eter measurement totals are typically expressed in linear
footage, or LF. To perform perimeter calculations, use the
following steps:
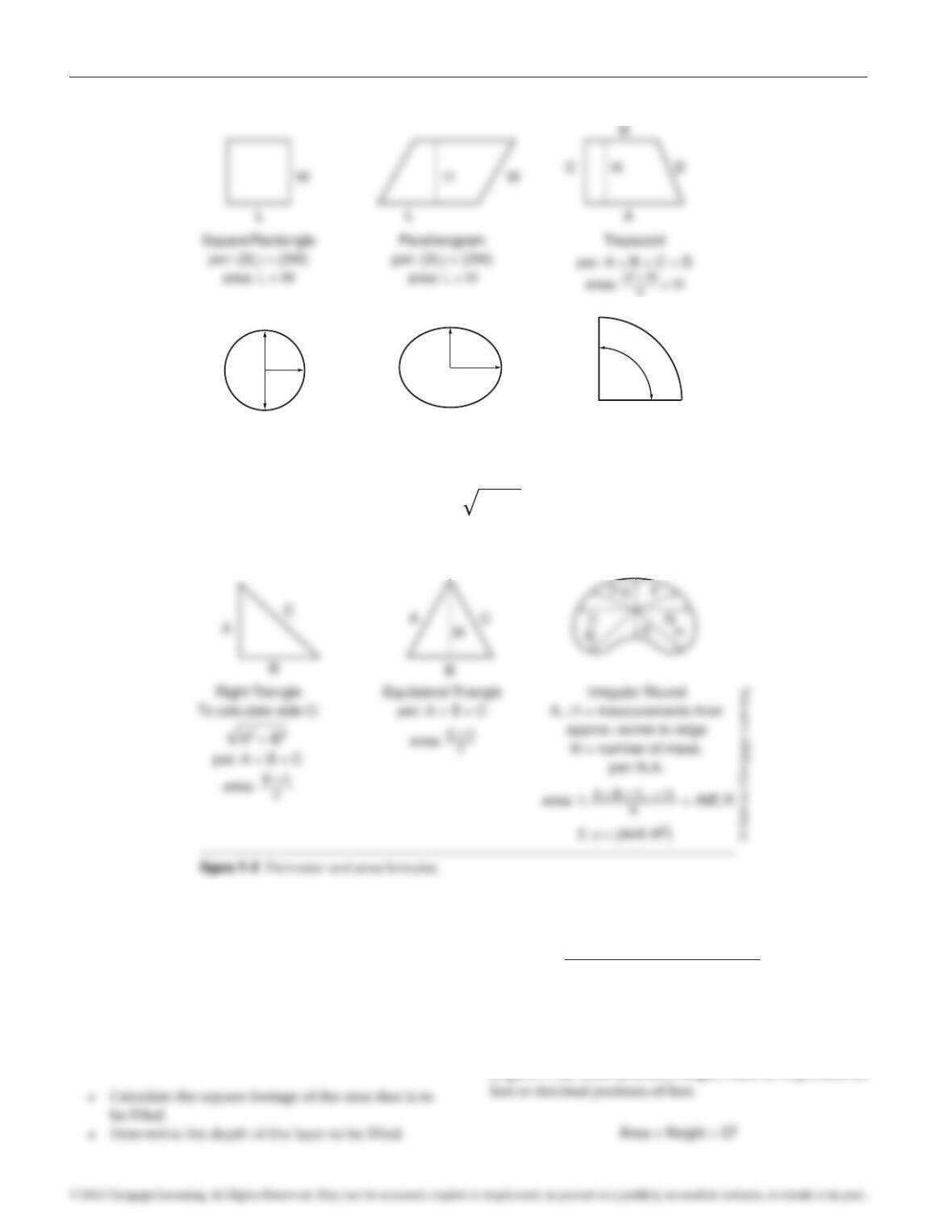
• Identify the subject being measured as one of the
standard geometric shapes identified in Table 1–1
or as an irregular shape.
• If the subject is a standard geometric shape,
perform the necessary linear measurements
required to calculate the shape’s perimeter. Use
the formula listed in Figure 1–2 to discern what
Area Measurements
Area calculations determine the surface area of objects
and spaces found in the landscape. Area measurement
totals are typically expressed in square footage, or SF.
Before performing area calculations, the contractor must
determine if the object or space being measured matches
a typical geometric form or is irregularly shaped.
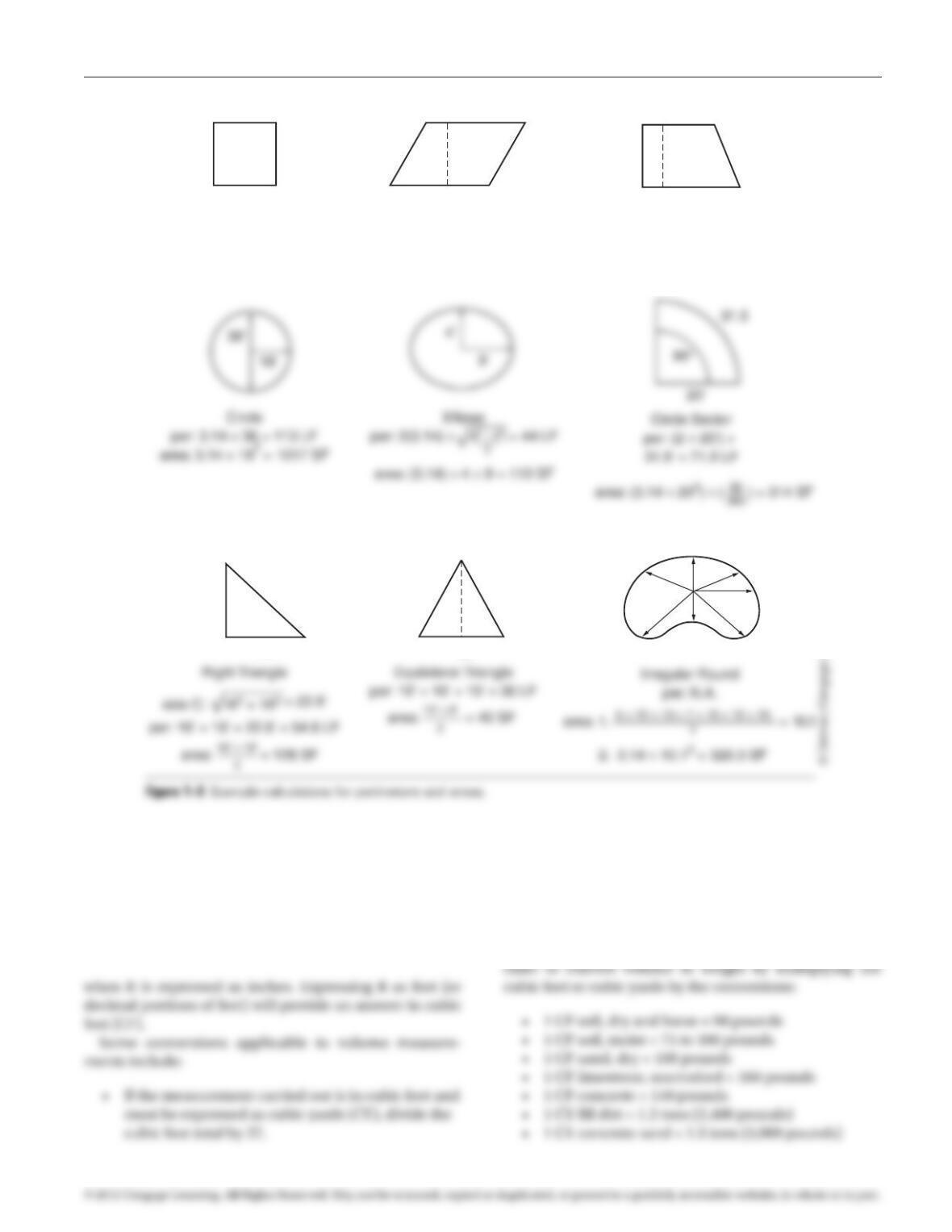
Area Measurements for Standard Geometric Shapes.
When an area calculation needs to be performed for an
• Perform the necessary linear measurements
required to calculate the subject’s area, as listed in
Figure 1–2.
• Use the formula listed in Figure 1–2 to calculate
the area. See Figure 1–3 for examples.
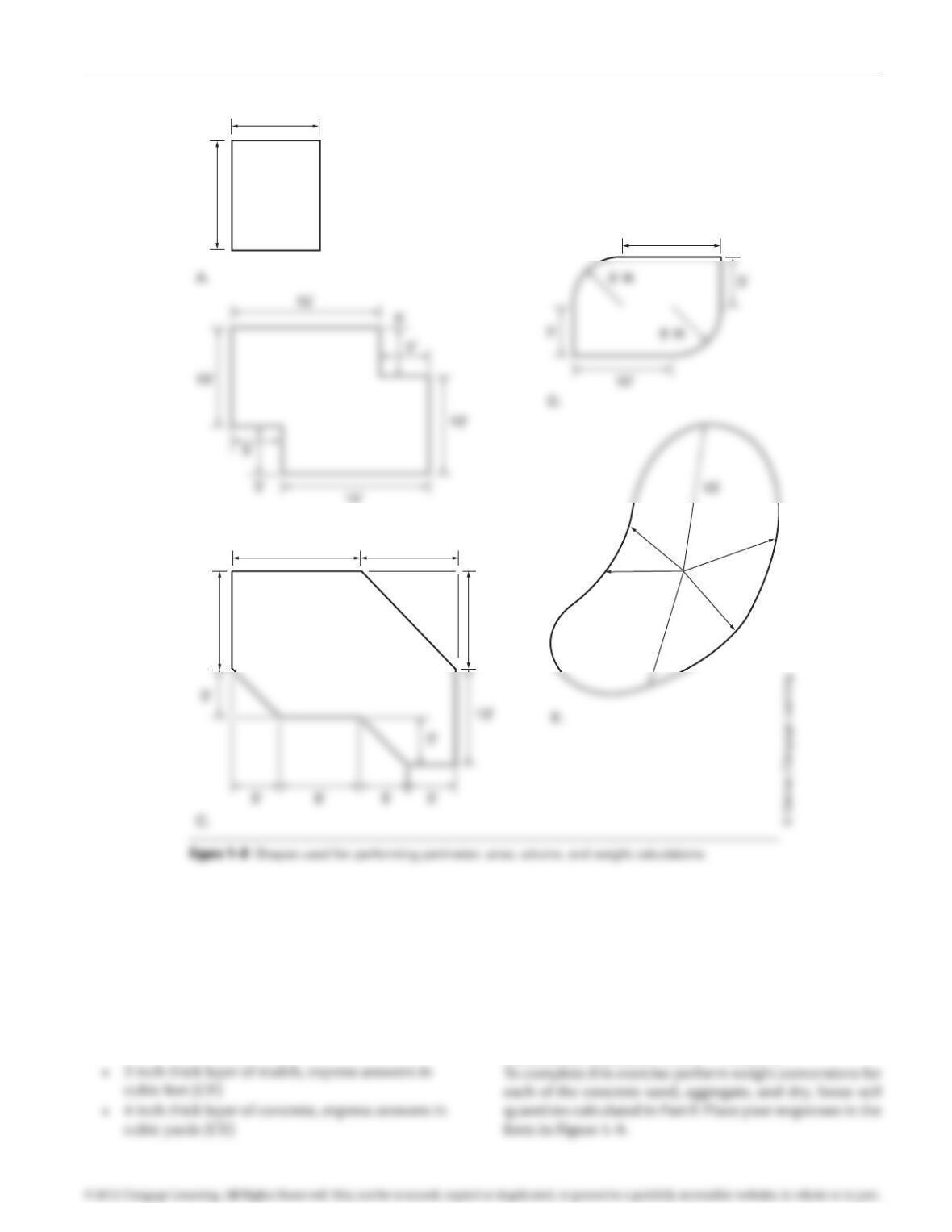
Area Measurements for Irregular Shapes. Most
objects and spaces in the landscape can be broken down
into a collection of shapes that approximate measurable
geometric forms. Once the dimensions of these shapes
calculate area by using the “sum of shapes” method, fol-
low these steps:
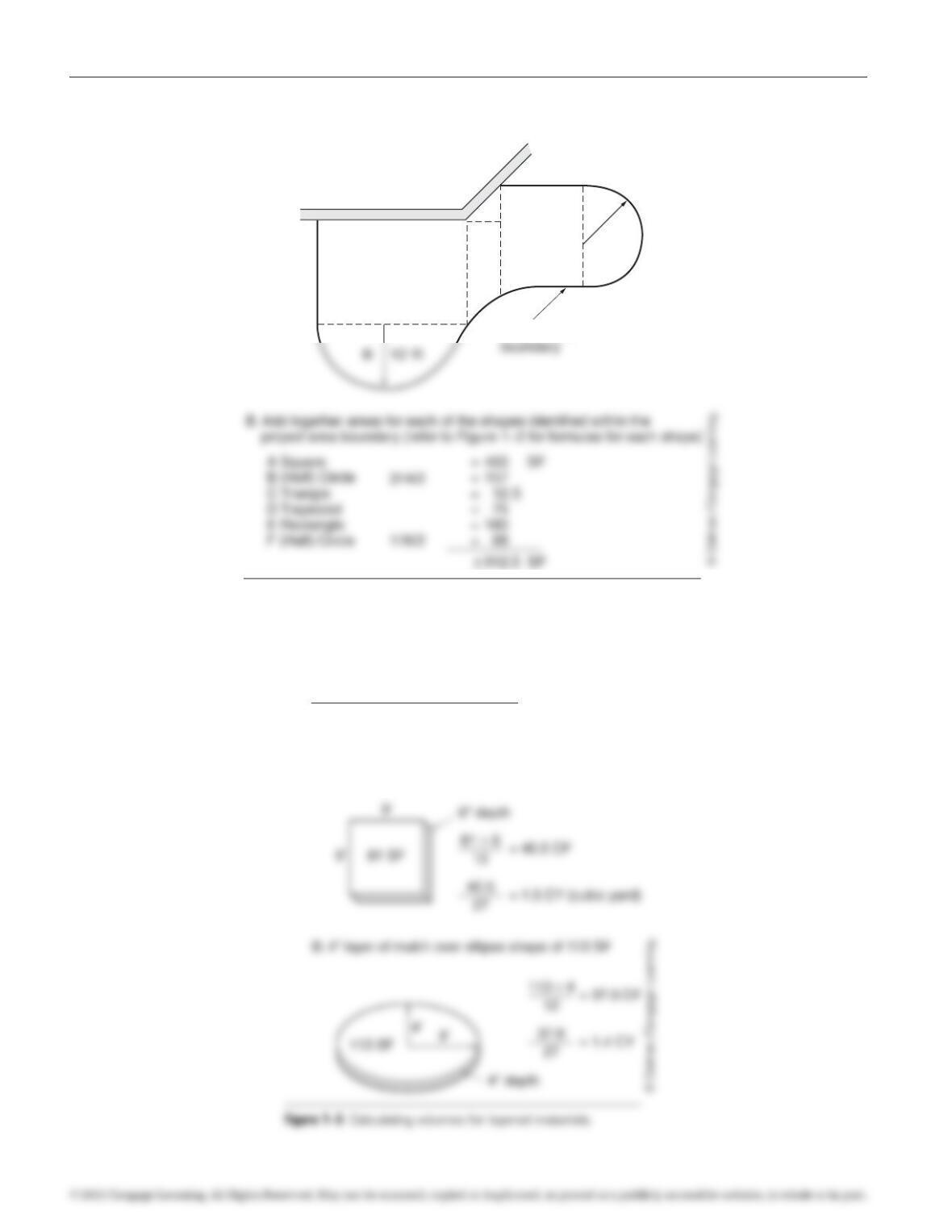
• Analyze the object or space for which an area
measurement is required. Observe what geometric
forms are recognizable within the boundaries of
the overall shape. These shapes should cover the
majority of the space being measured without
much overlap. (Figure 1–4, Step A.)
• Using the formulas in Figure 1–2, take the
necessary linear measurements and perform
the calculations required for each identified
shape.
• Total the answers to obtain the area for the entire
object or space. Be certain all calculations are
footage by 100. To obtain rolls of sod (each sod
roll being 1 SY), divide square footage by 9.
Conversions such as number of unit pavers require
the square footage derived from the previously
mentioned calculations and a conversion
number provided by the manufacturer of
the material (such as 4.5 bricks required for
every square foot of paved area). Multiply the
Exercise 1 Construction Math 3
97171_01_ch01_p001-010.indd 3 14/06/10 8:38 PM
conversion number by the squarefootage to
obtain a material quantity estimate.
Volume Measurements
Volume calculations provide the three-dimensional bulk,
or cubic, measurement of materials used in landscaping.
Volume measurement totals are typically expressed in
cubic footage, or CF. To calculate volumes for landscap-
ing, follow these steps:
• Place the numbers in the following formula:
Area (in SF) × Depth (in inches) = CF
12
Note that the depth is not converted to feet, but is left
in inches. Examples are shown in Figure 1–5. To calcu-
late the volume of a cylinder use the following formula
(Figure 1–6). Both area and height must be expressed as
4 Exercise 1 Construction Math
Circle
R = radius
D = diameter
π = pi, value of 3.14
per: πD
area: πR2
Ellipse
S = short radius
L = long radius
per: 2π
area: πSL
Circle Sector
θ = angle degrees
L = arc length
per: (2R) + L
area: πR2 ×
(
––
)
per = Perimeter
D
R
S
L
L
R
(S2 + L2)
2
360
θ
θ
–––––
97171_01_ch01_p001-010.indd 4 14/06/10 8:38 PM
Exercise 1 Construction Math 5
Calculating the volume of a sphere is a necessary first
step in determining the weight of plant rootballs. Once
the volume has been calculated, a weight conversion can
be used to convert to pounds. The formula for calculating
the volume of a sphere is as follows (Figure 1–6):
4.18 × R × R × R = CI (cubic inches)
• If the measurement carried out is in cubic inches
and must be converted to cubic feet, divide the
cubic inches total by 1,728.
Weight Calculations
Many landscape materials are purchased by weight rather
than by volume. For those materials use the following
Square/Rectangle
per: (2 × 9′) + (2 × 9′)
= 36 LF
area: 9′ × 9′ = 81 SF
Parallelogram
per: (2 × 20′) + (2 × 16′)
= 72 LF
area: 20′ × 14′ = 280 SF
Trapezoid
per: 12′ + 9′ + 10′ + 10.5′ = 41.5 LF
area: ––––– × 10′ = 105 SF
9′ 16′
9′
10.5′H = 10′10′
12′
14′
(12′ + 9′)
2
16′
C = 22.6
16′
10′ 10′
8′
10′
15′
12′
10′
5′
12′
10′
7′
9′ 20′
97171_01_ch01_p001-010.indd 5 14/06/10 8:38 PM
6 Exercise 1 Construction Math
A
20′
20′ D
C
5′
5′
10′
12′
E15′ F
7.5′ R
Project area
A. Identify shapes and measure dimensions of each
–
Figure 1–4 Calculating area for irregular shapes.
Volume formula:
Examples:
A. 6″ layer of topsoil over square shape of 81 SF
area (in SF) × depth (in inches) = CF (cubic feet)
12
97171_01_ch01_p001-010.indd 6 14/06/10 8:38 PM
Exercise 1 Construction Math 7
CI
1728
Volume of Sphere:
Formula: 4.18 × R × R × R = CI
Example: 4.18 × 8 × 8 × 8 = 2140 CI
Conversion to CF: –––––– = CF
2140
1728
–––––– = 1.24 CF
8″ R
• 1 CY aggregate (class 5 aggregate, 1 inch
roadstone, or equal) = 1.25 tons
• 2,000 pounds = 1 ton
Comprehensive Process of Converting
Measurements
If this section has been followed from beginning to end,
it should be apparent that primary measurements and
calculations, such as linear measurements and area
calculations, can be used to determine subsequent
numerical values during the course of a project.
eliminating the need to begin each calculation from
scratch using linear measurements.
PREREQUISITE EXERCISES
None.
MATERIALS REQUIRED
• Calculator
• Writing materials
• 100 foot tape measure or measuring wheel
97171_01_ch01_p001-010.indd 7 14/06/10 8:38 PM
8 Exercise 1 Construction Math
Figure 1–7 Calculating averages problem set.
139 27 18 9 3
)++++
=
n
24 2 16 7
)++ + =
n
614 11 21 39 22
)+++ + =
n
75 6 11 4
)++ + =
n
122 17 83 77
)....+++ =
n
233 76 91 26 10
)…..++++ =
n
615 53 6 33 7 2 1 11 3 2
)…..++++
=
n
7413 344 288
)…++ =
n
113 5
1
2
1
2
1
2
)++ =
n
2315
1
4
3
8
5
16
)++ =
n
n
695 11
6
8
7
16
1
4
)++ =
n
711 12 9 1
3
8
2
8
5
8
4
8
)+++
=
n
n
EXERCISE DESCRIPTION—PART C
To complete this exercise, perform direct measurements
and estimations of linear dimensions for objects identi-
fied by the instructor.
EXERCISE DESCRIPTION—PART E
To complete this exercise perform area calculations for
each of the shapes shown in Figure 1–8. Place your
responses in the form in Figure 1–9.
© Delmar/Cengage Learning.
97171_01_ch01_p001-010.indd 8 14/06/10 8:39 PM
Exercise 1 Construction Math 9
10′
12′
13′ 10′
10′ 10′
15′
10′
10′
12′
8′ 8′
7′
B.
following materials. Place your responses in the form in
Figure 1–9.
• 1 inch thick layer of concrete sand, express
answers in cubic yards (CY)
• 6 inch thick layer of aggregate base material,
express answers in cubic yards (CY)
• 8 inch thick layer of dry, loose soil, express
answers in cubic yards (CY)
EXERCISE DESCRIPTION—PART G
97171_01_ch01_p001-010.indd 9 14/06/10 8:39 PM
10 Exercise 1 Construction Math
Shape
A B C D E
Measurement
Perimeter
Area
Volume (CY)
6″ aggregate
Volume (CY)
8″ soil
97171_01_ch01_p001-010.indd 10 14/06/10 8:39 PM