Unit 19 Solutions
245
Unit 19 Problem Solutions
19.1 See FLD p. 777 for solution. 19.2 See FLD p. 777 for solution.
19.3 See FLD p. 778 for solution. 19.4 See FLD p. 778 for solution.
19.11 19.12 (a)
19.12 (b)
Unit 19 Solutions
246
19.13
S0
0
Reset
X
19.14 (a)
19.14 (b) Let S0, S1, S2 and S3 be the four FF outputs, then
D0 = x’(S0 + S1 + S2 + S3),
D1 = xS0,
19.14 (c) Using state assignment S0 = 00, S1 = 01, S2 = 10
and S3 = 11, and denoting state variables Q1 and
Q0, D1 is the OR of D2 and D3 from Part b) so
Unit 19 Solutions
247
S1
0
K
0
1
Reset
St
So
0
1
So0
Sh, SI Sh
19.15 (a)
D1 = K’Q1 + K’SoQ0 , D0 = K’Q0 + StQ0‘
Next State Table for Q1+ Q0+: S1 = 00, S2 = 01 and
S3 = 11.
St K So
Q1Q0000 001 011 010
00 00 00 00 00
01 01 11 00 00
11 11 11 00 00
10 — — — —
Output Table for Clr Sh Er SI
St K So
Q1Q0000 001 011 010
00 0000 0000 0000 0000
Er = KSoQ1‘Q0; SI = K’So‘Q1 + KSoQ1‘Q0
19.15 (b)
Label the three FF outputs S1, S2 and S3.
D1 = St’S1 + KS2 + KS3; D2 = K’So‘S2 + StS1
D3 = K’SoS2 + K’S3; Clr = StS1
Sh = K’S2 + KSo‘S2 + K’S3 = K’S2 + So‘S2 + K’S3
19.15 (c) Label the two FF outputs Q1, Q0 and the decoder
outputs S1 = 00, S2 = 01 and S3 = 11*, then
D0 = K’So‘S2 + StS1 + K’SoS2 + K’S3
= K’S2 + StS1 + K’S3
19.15 (d)
Unit 19 Solutions
248
St
M
Done
Load
Sh
19.18
1
X
Clock
State S0S2S0S2S1S2S0
S1
19.19 (a)
State Q0
Q1
St M K Q0
+ Q1
+ Ad Sh Load Done
S0 0 0 0 – – 0 0 0 0 0 0
S0 0 0 1 – – 0 1 0 0 1 0
19.19 (b)
A+ = A’BX2 + A’B’X2 (X1
‘ + X3 ) + {AB}
= BX2 + A’X2 (X1
‘ + X3 )
B+ = A’B’ (X2
‘ + X1X3
‘ ) + AB’X1
‘ + A’BX2
‘ + {AB}
= AX1
‘ + A’B’X1X3
‘ + A’X2
‘
19.16
S /
S /
S /
S1 /
S /
S /
S / Done
0 1 3 5
7 9
Clock
State
St
S0S1S2S2S3S3S4
19.17
Unit 19 Solutions
249
PLA table obtained by tracing link paths:
State AB X1X2X3 A+B+ Z1Z2Z3
S0
00 – 0 – 01 010
00 01 – 10 101
00 110 01 100
19.19 (c) 25 × 5 ROM
AB X1X2X3 A+B+ Z1Z2Z3
00 000 01 010
00 001 01 010
19.19 (d)
S0/LC, LR
s
S1/SR
01
Reset
19.20 (a) C is loaded with 0.
19.20 (b)
S0/LC, LR
s
S1/SR
01
Reset
19.21 (b)
19.21 (a) C is loaded with 0.
Unit 19 Solutions
250
S0/LC, LR
s
S1/IncC
01
Reset
S2/IncC
19.22 (a) C must be at least 4 bits and is loaded with 810
(10002).
19.22 (b)
S0/LC, LR
s
S1/SR, IncC
01
Reset
S2/SR, IncC
1
z
19.23 (a) C must be at least 4 bits and is loaded with 710
(01112).
19.23 (b)
S0/LC, LR
s
S1/SR, IncC
01
Reset
S2/SR, IncC
S3/SR, IncC
S4/SR, IncC
19.24 (a) C must be at least 4 bits and is loaded with 810
(10002).
19.24 (b)
Unit 19 Solutions
S0
s
0
Reset
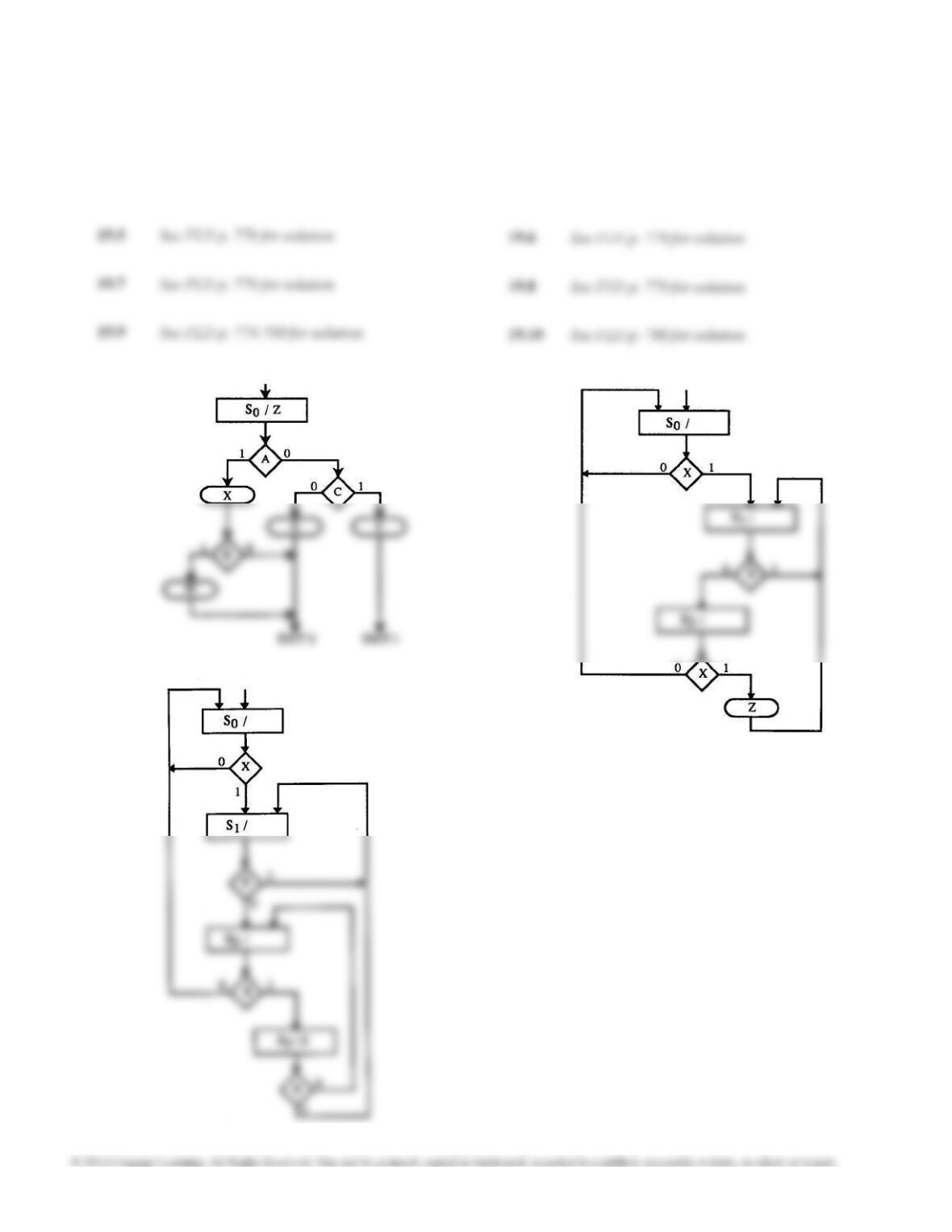
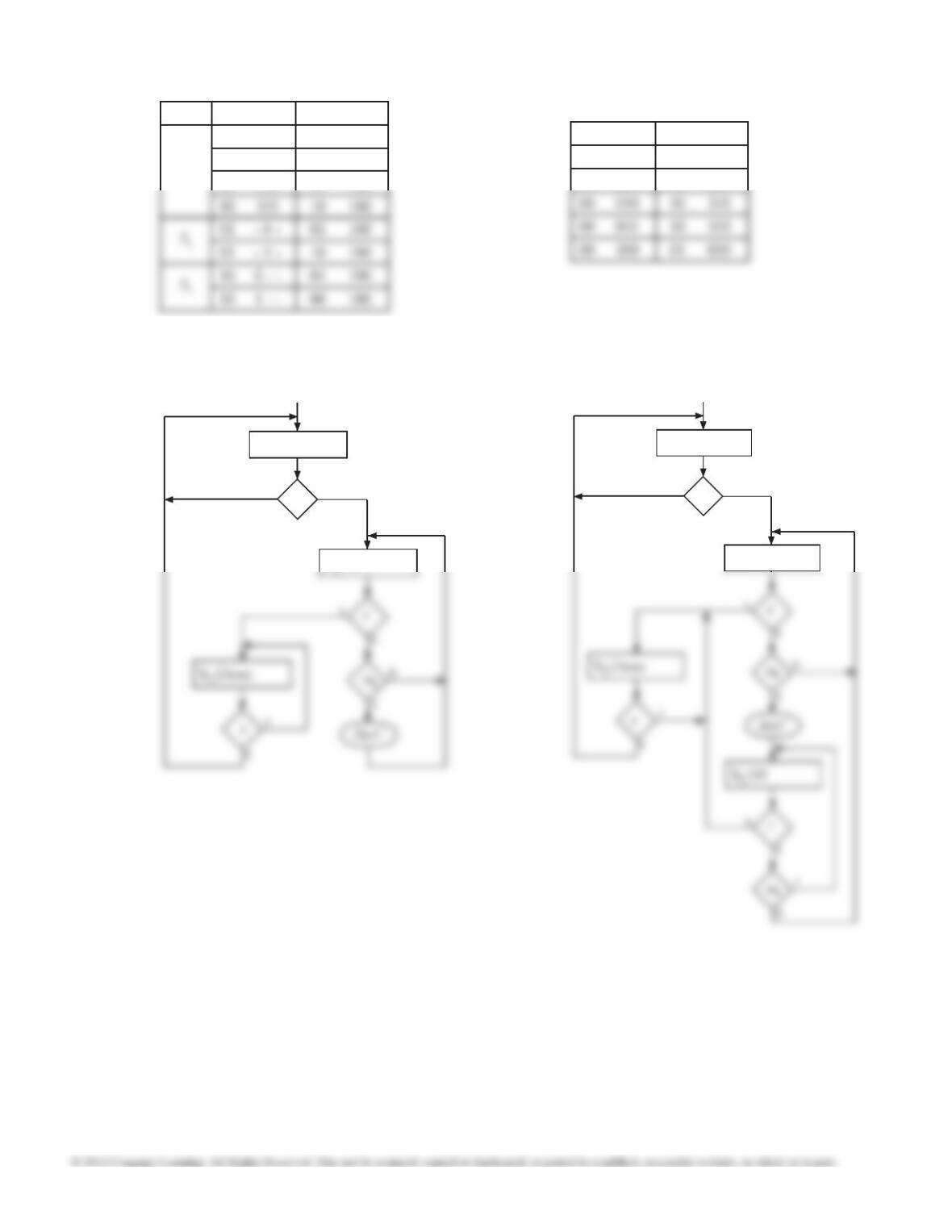
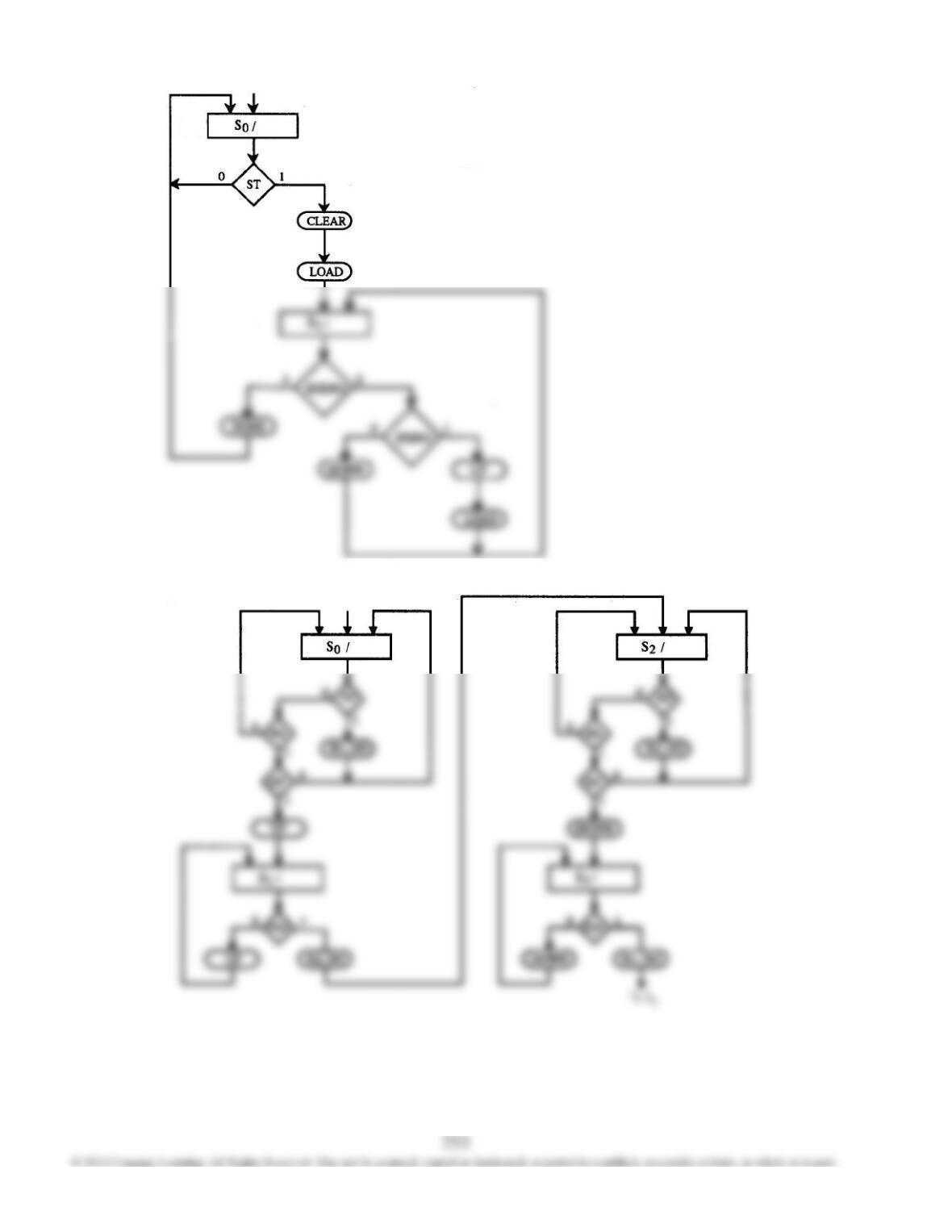
19.25 (a) Let S0, S1, S2 and S3 be the four FF outputs, then
D0 = s’(S0 + S3); D1 = sS0 + (TC)‘S2
D2 = S1; D3 = (TC)S2
LDN = S1 + S2 or LDN = S1 + S2 + S3
CE = S1 or CE = S1 + S3
z1 = S1; z2 = S2
P3 = 0; P2 = 0; P1 = 1; P0 = 1
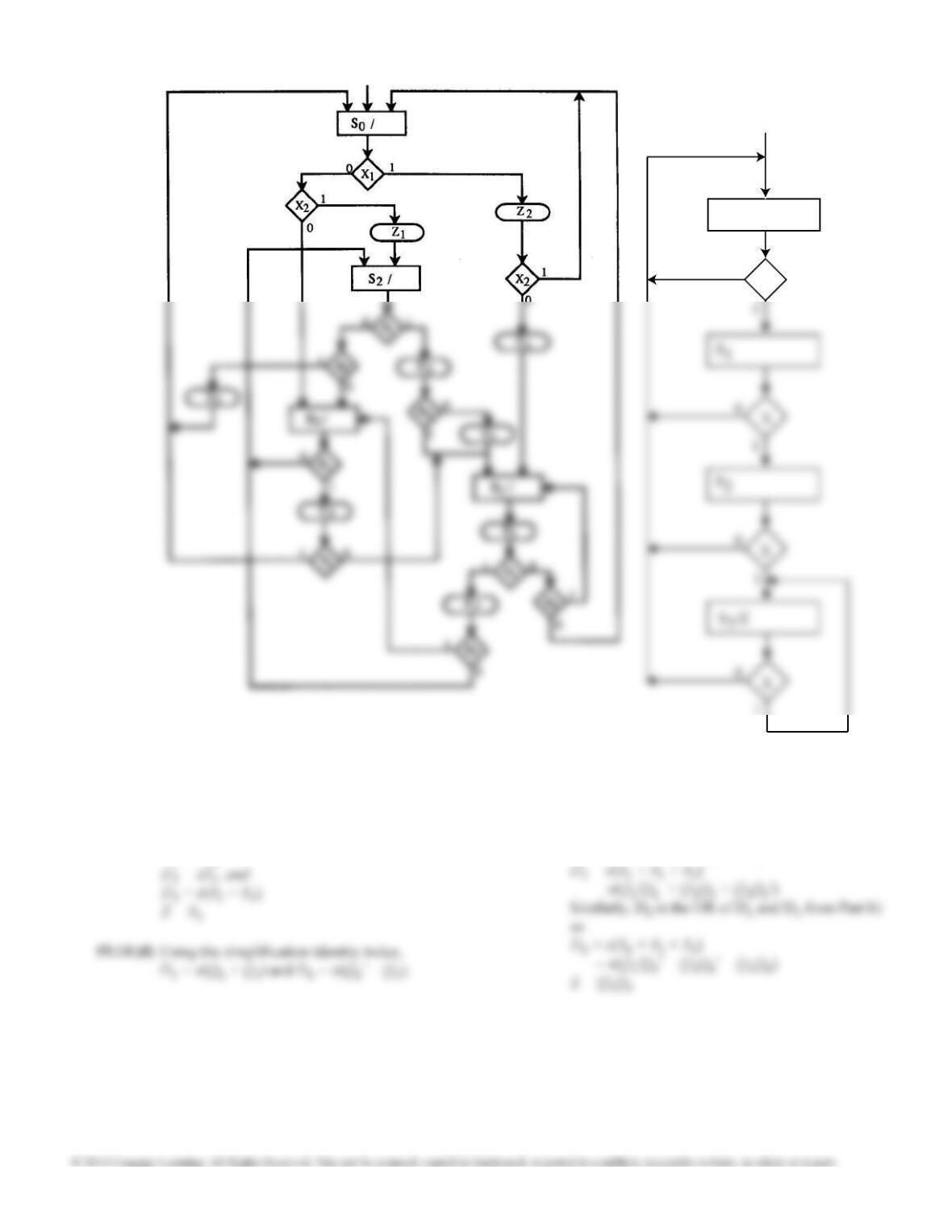
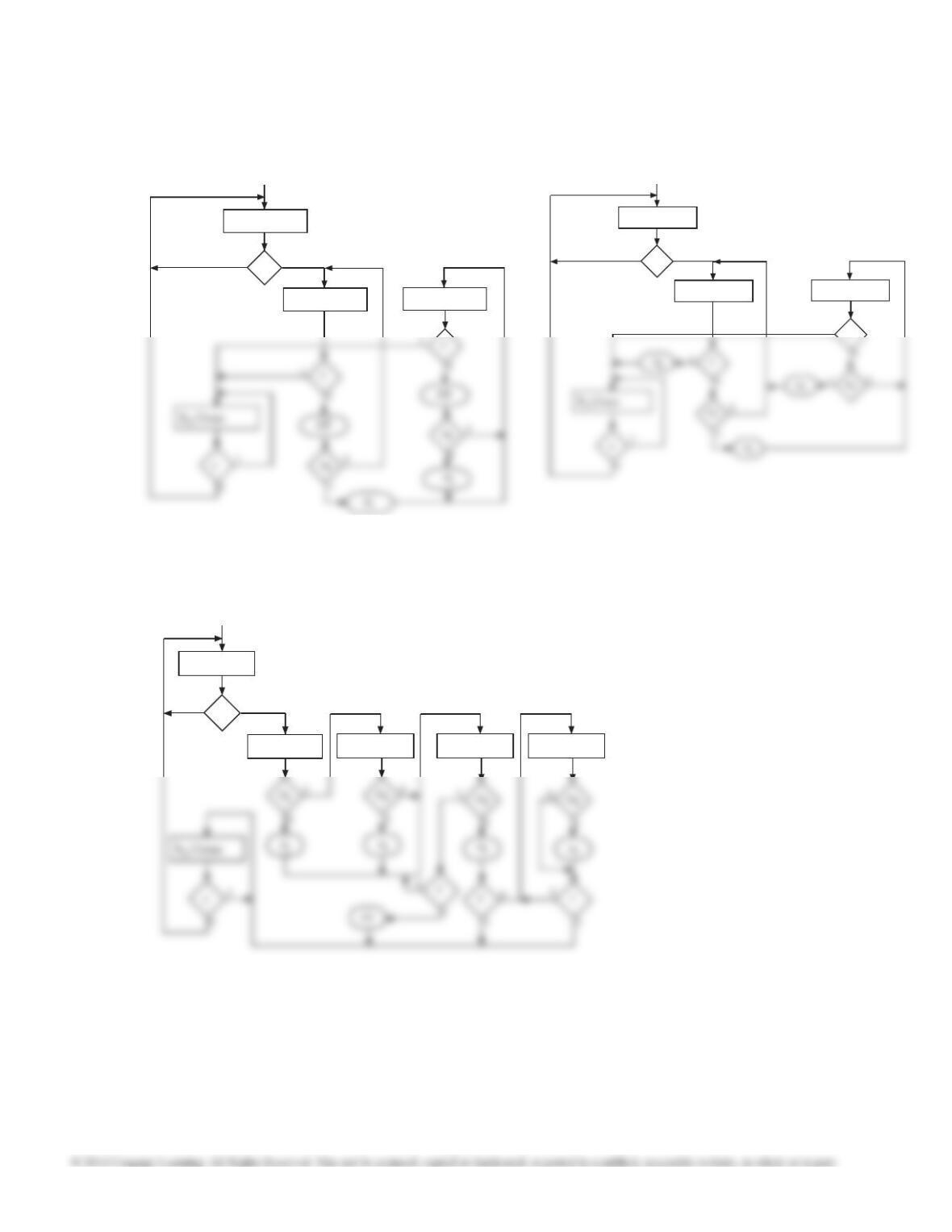
19.25 (b)
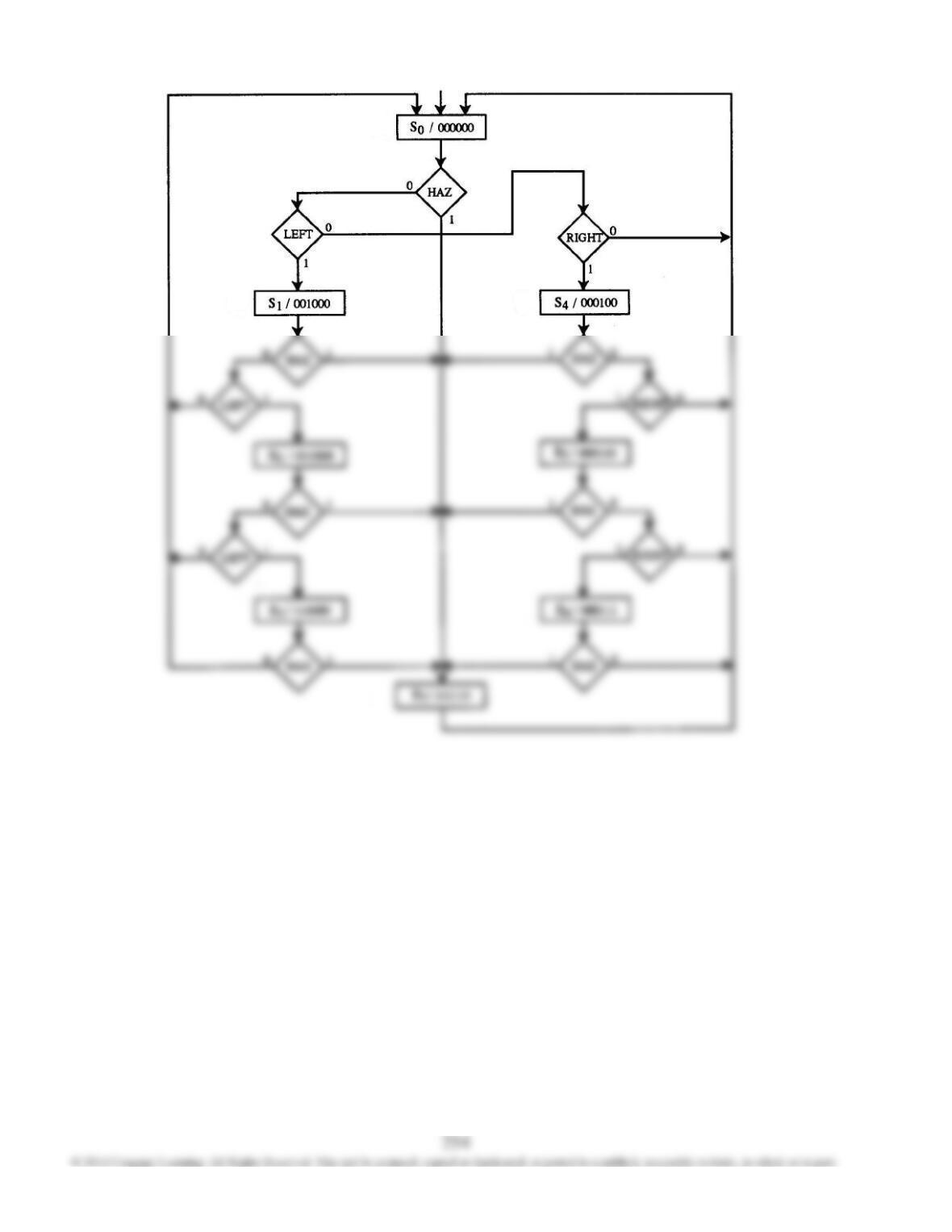
Using state assignment S0 = 00, S1 = 01, S2 = 11,
S3 = 10, and denoting the state variables as Q1 Q0,
D1 is the OR of D2 and D3 from Part (b) so
D1 = S1 + (TC)S2 = Q1‘Q0 + (TC)Q1Q0
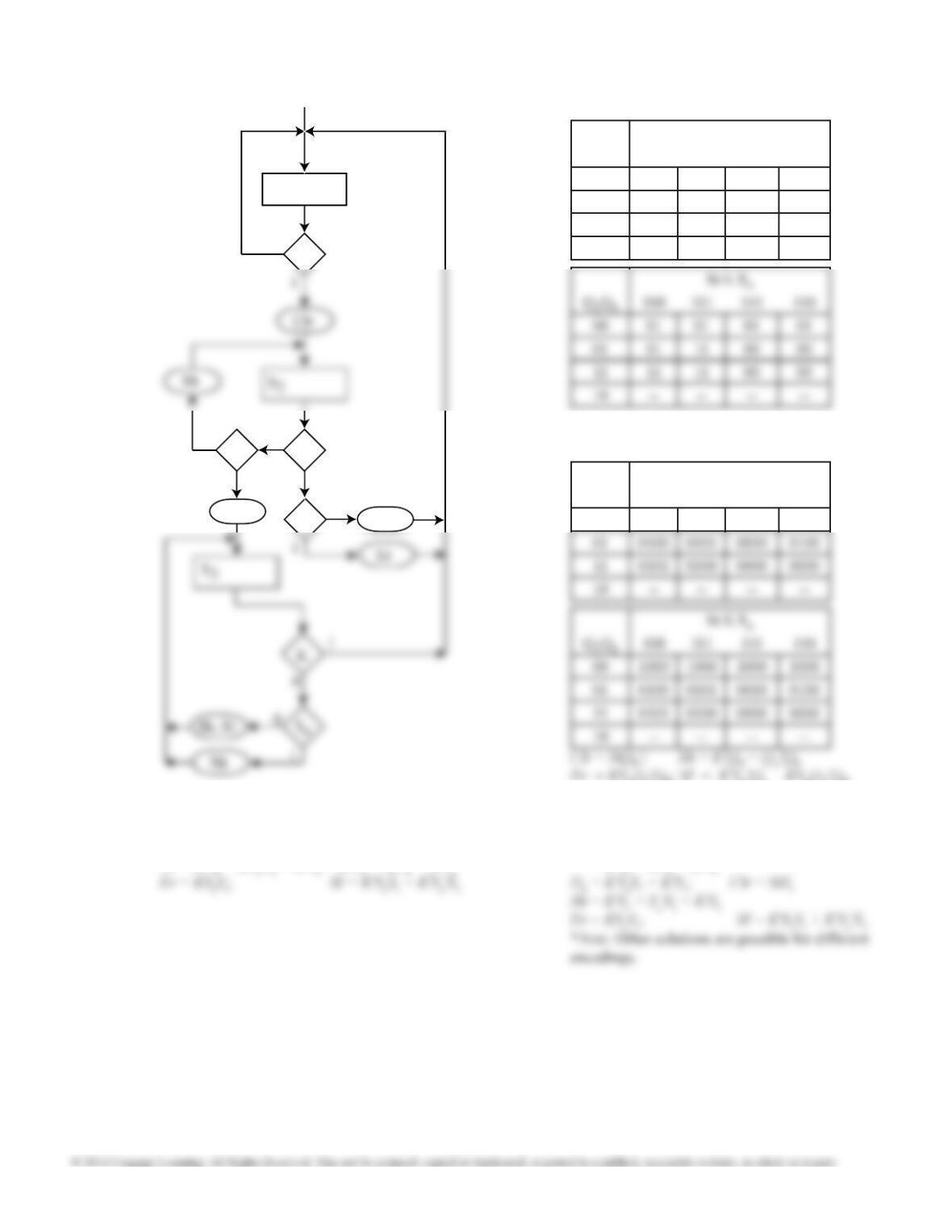
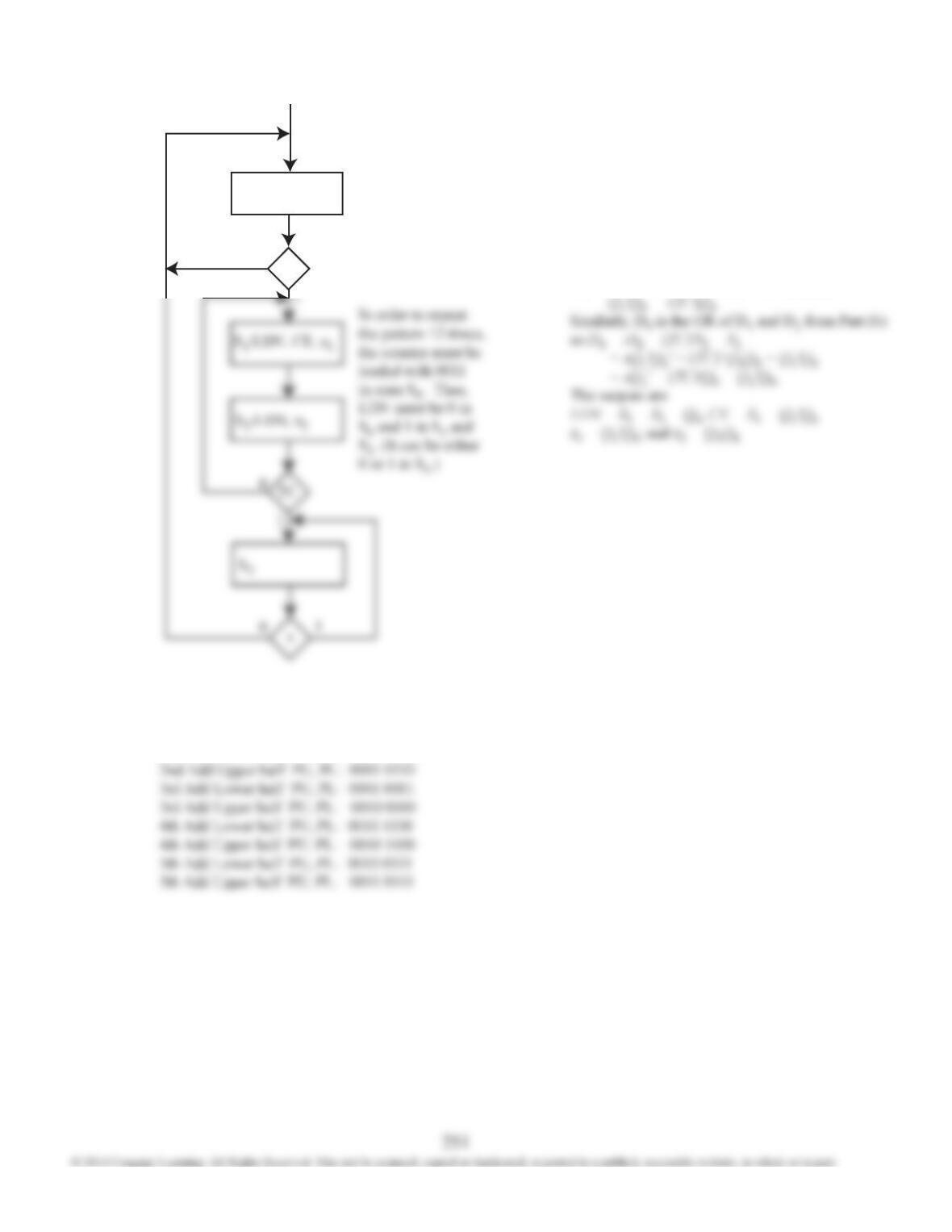
19.25 (c)
Initial PU,PL: 0000 0000
1st Add Lower half PU, PL: 0000 1011
1st Add Upper half PU, PL: 0000 1011
2nd Add Lower half PU, PL: 0000 0110
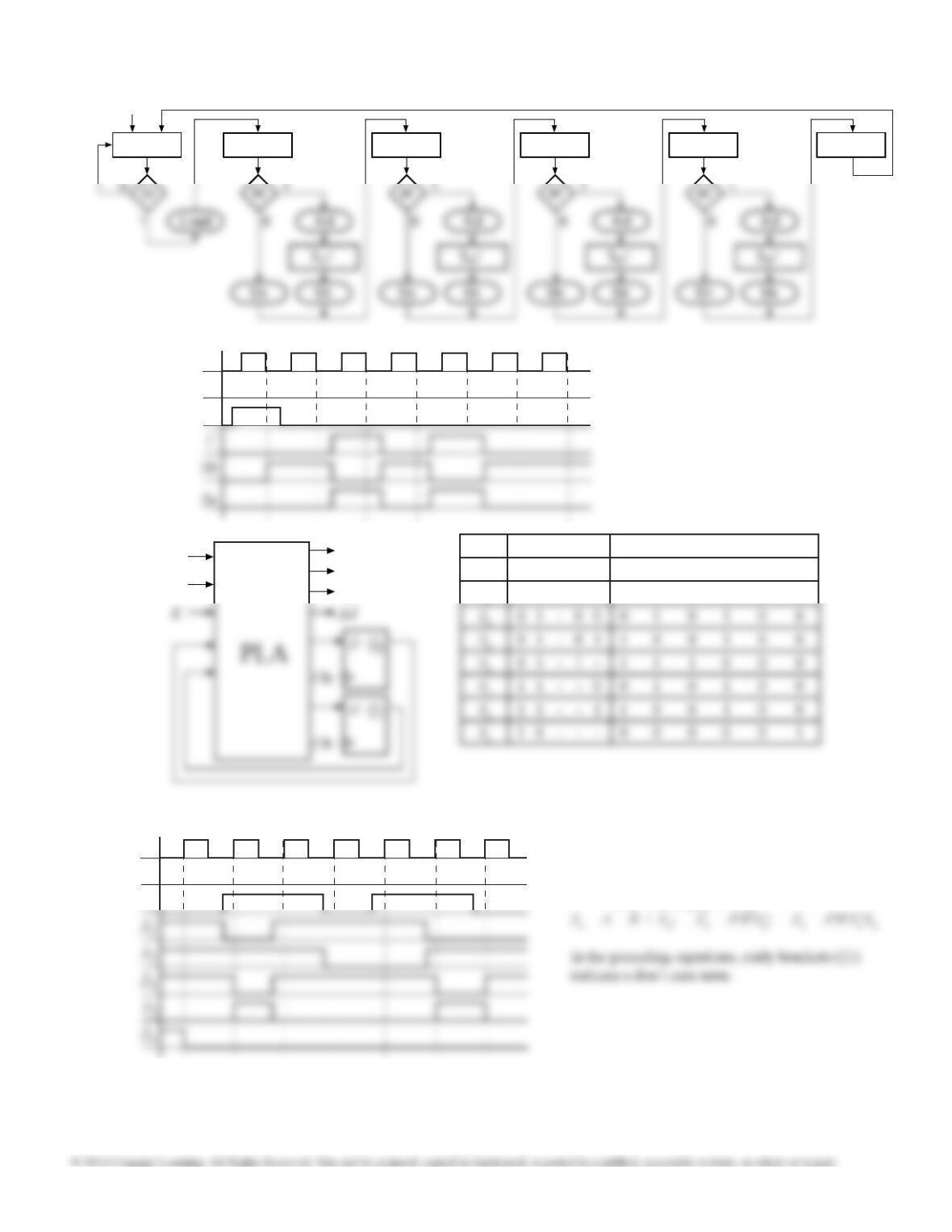
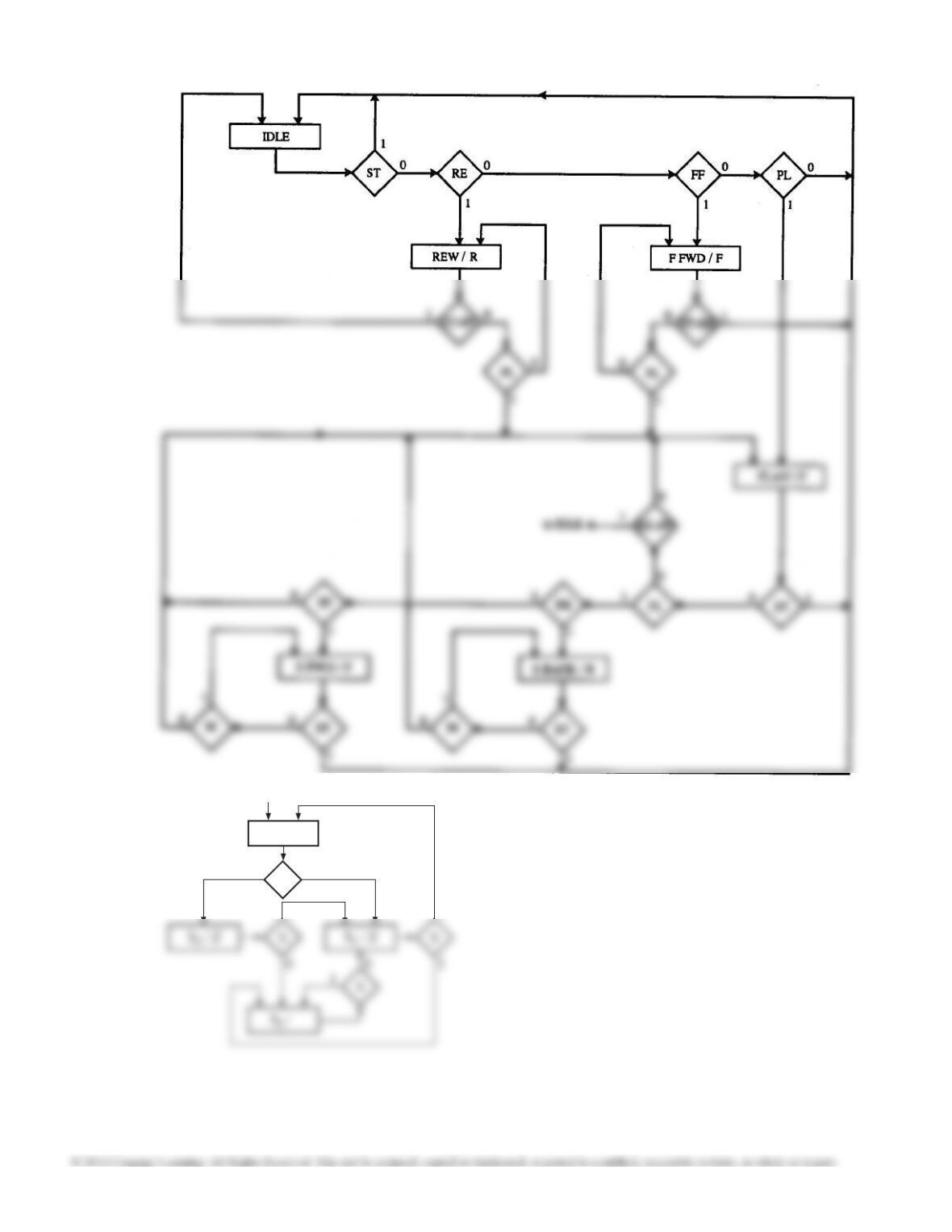
19.26 (a)
Unit 19 Solutions
252
S0/CP, LA, LB, CC
S
0
1
S1/
Reset
1
19.26 (b)
Label the 4 FF outputs S0, S1, S2 and S3.
D0 = S’S0 + S’S3
D1 = S(S0) + S2
19.26 (c)
Assume two FFs Q1Q0 and the following encoding:
S0 = 00, S1 = 01, S2 = 11 and S3 = 10. (The
decoder outputs are labeled S0, S1, S2 and S3.)
19.26 (d)
S
0
1
LA,LB,CC,CP
SB*
S1/
S2/
19.27
Unit 19 Solutions
19.28 (a) See answer to 18.30 (b).
19.28 (b)
19.29 (a)
See answer to 16.26 (c).
19.29 (b)
Unit 19 Solutions
19.30
Unit 19 Solutions
255
19.31
19.32
1
X
S /
0
10
0
Unit 19 Solutions
256