Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
201
Unit 16 Solutions
i
x
a
i
'
i
x
ai
i+1
b
i
b'
i+1
aZ
16.17 (b)
State
Next State
X = 0 X = 1
Z
S0 S0 S10
S0
0 1
0
1S2
S1
S3
ai
bi
State
aibi
ai+1bi+1
X = 0 X = 1
Z
S000 00 10 0
xi
ai bi0 1
00
0
1
bi+1 = bi
' + xiai
16.17 (c)
xi
ai bi0 1
00
01
11
10
0
1
0
1
0
1
1
1
Unit 16 Problem Solutions
16.15 See FLD p. 767 for solution.
16.17 (a) The state meanings are given in the following table:
Name Meaning
S0No 1’s have occurred
16.16 See FLD p. 768 for solution.
1
S3
1
S2
0
0
S0
0
S1
0
1 1
16.1 -
16.14
See Lab Solutions in this manual.
Since no 1’s have occurred, a1 and b1 are the same
as S0 or, a1 = 0; b1 = 0;
202
Unit 16 Solutions
DQ
x
i
a
i
a
i+1
16.17 (d)
ai
ai+1 yi
xi = 0 xi = 1 xi = 0 xi = 1
16.18 (a)
16.18 (a)
yi
aibi
ai+1bi+1
xi yi =
00
xi yi =
01
xi yi =
11
xi yi =
10
00 00 10 00 01
16.19 (a)
aibi
ai+1bi+1
xi yi =
00
xi yi =
01
xi yi =
11
xi yi =
10
00 00 10 00 01
16.20 (a)
16.20 (b) ai+1 = aixi' + aiyi + aibi + bi'xi'yi
bi+1 = bixi + biyi' + ai'bi + ai'xiyi'
16.20 (c) Z1 = an+1bn+1'
Si
Si+1
xi yi =
00
xi yi =
01
xi yi =
11
xi yi =
10
Initial S-1 S0S1S3S2
16.20 (d)
203
Unit 16 Solutions
16.21 (a)
S0S1
11
10
Present
State
Next State
X = 0 1
Output
X = 0 X = 1
S0 S2 S1 0 0
S1 S3 S0 0 1
S2 S0 S3 1 0
1S1
S2
The state meanings are given in the following table:
Name Meaning
S0even #0's and even #1's received
The output becomes 1 whenever an even #0's or an
even #1's (greater than 0) occurs.
A B
A+ B+
X = 0 1
Z
X = 0 X = 1
DA
X
A B 0 1
00
01
1
1
0
0
DB
X
A B 0 1
00
01
1
0
1
0
Z
X
A B 0 1
00
01
0
0
0
1
16.21 (b)
A B
JA KA
X = 0 1
0 0 1 X 0 X
0 1 1 X 0 X
A B
JB KB
X = 0 1
0 0 1 X 1 X
0 1 X 1 X 1
KAX
A B 0 1
00
X
X
JA
X
A B 0 1
00
1
0
204
Unit 16 Solutions
JB
X
A B 0 1
00
01
1
X
1
X
16.21 (b)
(cont.) KB
X
A B 0 1
00
01
X
1
X
1
The state meanings are given in the following table:
Name Meaning
S0reset state
S1even #0's and even #1's received
S2odd #0's and even #1's received
16.21 (c)
16.21 (c)
(cont.) 0
S0
0
S1
1
S5
0
S2
0
1
0
0
1
1
Present
State
Next State
X = 0 1 Z
S0 S2 S5 0
S1 S2 S5 1
S2 S1 S6 0
S3 S1 S6 1
Guidelines: I: (0, 1)2x, (2, 3)2x, (4, 5)2x
II: (2, 5)2x, (1, 6)4x, (3, 4)
An assignment is
A
B C 0 1
00
01
S0
S1
S5
S4
S0000 110 100 0
S1001 110 100 1
S6011 101 111 0
-- 010 --- --- -
205
Unit 16 Solutions
Z
X A
B C 00 01 11 10
00
01
0
1
0
1
0
1
0
1
TCX A
B C 00 01 11 10
00
01
0
1
1
0
0
1
1
0
TBX A
B C 00 01 11 10
00
01
1
1
1
1
0
0
0
0
TAX A
B C 00 01 11 10
00
01
1
1
1
1
1
1
1
1
16.22 (a)
S1
S0S2
1
1
1
0
0
0
0
01
1
carry
carry
carry
16.22 (b) JAX
A B 0 1
00
01
0
0
0
1
KAX
A B 0 1
00
01
X
X
X
X
JBX
A B 0 1
00
01
0
X
1
X
KBX
A B 0 1
00
01
X
1
X
0
Z
X
A B 0 1
00
0
1
A B X DA DB Z
- 1 1 1 0 0
16.22 (c)
16.21 (c)
(cont.)
206
Unit 16 Solutions
16.23 (a)
S0
00
S1
00
S2
00
11-,
1-1
00-,
0-0
00-,
011,
100
11-, 1-1
00-, 0-0
011,
100
011,
100
Inputs: X2X1X0Outputs: ID
D0 = X2'X1X0 + X2X1'X0'
D1 = (X2'X1' + X2'X0')(Q0 + Q2 + Q4 + Q6)
D3 = (X2'X1' + X2'X0')Q1
D5 = (X2'X1' + X2'X0')(Q3 + Q5)
D2 = (X2X1 + X2X0)(Q0 + Q1 + Q3 + Q5)
D4 = (X2X1 + X2X0)Q2
D6 = (X2X1 + X2X0)(Q4 + Q6)
I = Q5
D = Q6
16.23 (b)
Using the assignment S0 = 000, S1 = 001, S2 = 010, S3 = 011, S4 = 100, S5 = 101,
S6 = 110, S7 = 111:
D0 = (X2'X1X0 + X2X1'X0')(S0 + S1 + S2 + S3 + S4 + S5 + S6)
= (X2'X1X0 + X2X1'X0')(Q0' + Q1' + Q2')*
= X2'X1X0 + X2X1'X0'*
16.23 (c)
16.24 (a)
11-,1-1/0000-,0-0/00
Inputs: X2X1X0Outputs: ID
S0
011,100/00
011,
100
011,
100
D0 = X2'X1X0 + X2X1'X0'
D1 = (X2'X1' + X2'X0')(Q0 + Q2 + Q4)
D3 = (X2'X1' + X2'X0')(Q1 + Q3)
D2 = (X2X1 + X2X0)(Q0 + Q1 + Q3)
D4 = (X2X1 + X2X0)(Q2 + Q4)
I = (X2'X1' + X2'X0')Q3
D = (X2X0 + X2 X1)Q4
16.24 (b)
207
Unit 16 Solutions
Using the assignment S0 = 000, S1 = 001, S2 = 010, S3 = 011, S4 = 100:
D2 = X2X0Q1Q0' + X2X1Q1Q0' + X2X0Q2 + X2X1Q2 or
16.24 (c)
16.25 (a) S0
000
S1
001
S6
110
01,
10
00,
11
01, 10
00, 11
Inputs: XY Outputs: Z2Z1Z0
10
D0 = 0
D1 = (X'Y' + XY)(Q0 + Q4 + Q5 + Q6)
D2 = (X'Y' + XY)Q1
D3 = (X'Y' + XY)(Q2 + Q3)
D6 = (X'Y + XY')(Q0 + Q1 + Q2 + Q3)
D5 = (X'Y + XY')Q6
16.25 (b)
Using the assignment S0 = 000, S1 = 001, S2 = 010, S3 = 011, S4 = 100, S5 = 101, S6 = 110:
D0 = (X'Y' + XY)(S0 + S4 + S5 + S6 + S2 + S3) + (X'Y + XY')S6
= (X'Y' + XY)(Q0' + Q2'Q1 + Q2Q1') + (X'Y + XY')Q2Q1Q0'
16.25 (c)
16.26 (a)
01,10/110
00,11/001
Inputs: XY Outputs: Z2Z1Z0
S0
S6
S1
01,10/110
D0 = 0
D1 = (X'Y' + XY)(Q0 + Q5 + Q6)
D2 = (X'Y' + XY)(Q1 + Q2)
D6 = (X'Y + XY')(Q0 + Q1 + Q2)
D5 = (X'Y + XY')(Q6 + Q5)
16.26 (b)
208
Unit 16 Solutions
Using the assignment S0 = 000, S1 = 001, S2 = 101,
S6 = 111, S5 = 011
D2 = Q1'Q0 + XY'Q1' + X'YQ1' or
D0 = 1
Z2 = X'Y + X Y'
Z1 = Q1'Q0 + XY'Q1' + X'YQ1' or
= Q1'Q0 + XY'Q0' + X'YQ1' or
16.26 (c) 16.27 (a) S0
000
S2
S6
01,
00,
Inputs: XY Outputs: Z2Z1Z0
01,
10
01,
10
00,
11
00,
11
10
D0 = 0
D1 = (X'Y' + XY)(Q0 + Q4 + Q5 + Q6 + Q7)
D2 = (X'Y' + XY)Q1
D3 = (X'Y' + XY)(Q2 + Q3)
16.27 (b) Using the assignment S0 = 000, S1 = 001, S2 = 010,
S3 = 011, S4 = 100, S5 = 101, S6 = 110, S7 = 111:
D0 = (X'Y' + XY)(S0 + S4 + S5 + S6 + S7 + S2 +
S3) + (X'Y + XY')(S0 + S1 + S2 + S3 + S6)
16.27 (c)
16.28 (a)
01,10/111
00,11/001
Inputs: XY Outputs: Z2Z1Z0
S0
209
Unit 16 Solutions
Using the assignment S0 = 000, S1 = 001, S2 = 100,
S5 = 011, S6 = 010, S7 = 111:
D2 = X'YQ1' + XY'Q1' + Q1'Q0
16.28 (c)
16.29 (b) Name Meaning
S0Staying on first oor
S1Moving from first to second oor
S2Staying on second oor
S3Moving from second to first oor
S1
FS'2UP
FS2R2DO
N2R2DO,
N1R1DO,
N1'N2DC
UP
16.29 (a) Ni = Qi
+ = (Qi + FBi + CALLi)Ri
'
= QiRi
' + FBiRi
' + CALLiRi
'
16.30 (a)
S0
000000
L'R'H'
H'
H'
L'H' LR'H'
L'RH' R'H'
210
Unit 16 Solutions
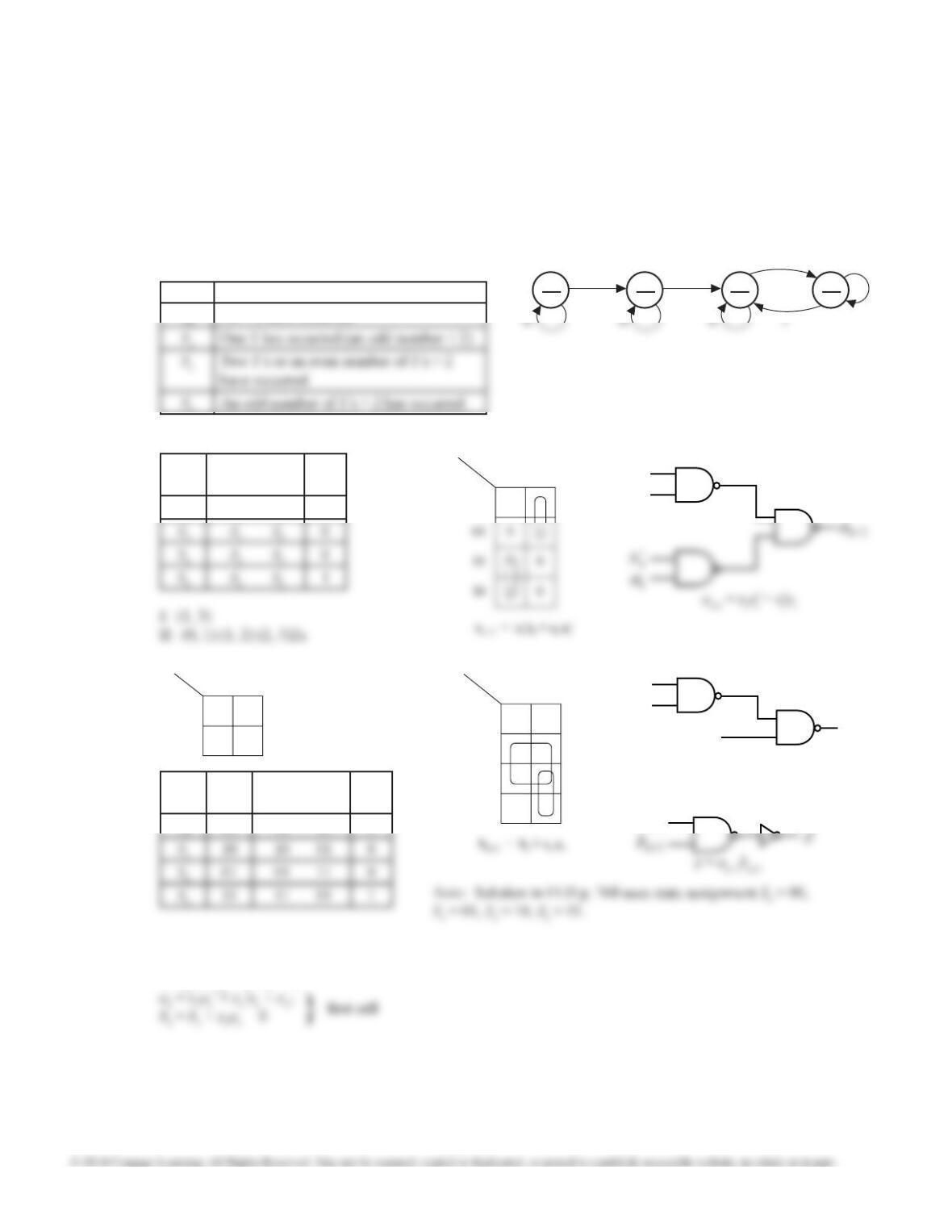
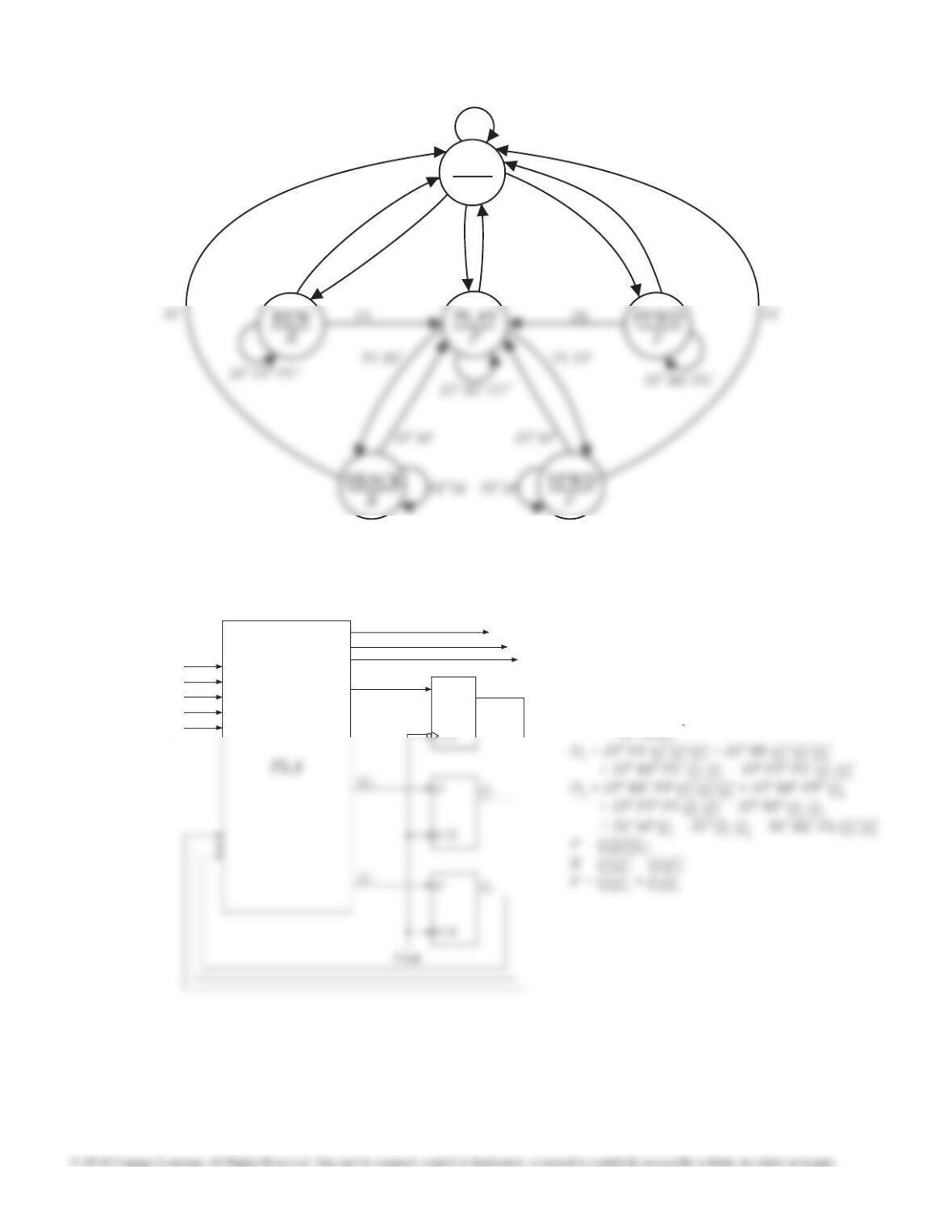
16.30 (b) First, assign LC = Q1, LB = Q2, LA = Q3, RA = Q4, RB = Q5, RC = Q6. So S0 = 000000, S1 = 001000, S2 = 011000, etc.
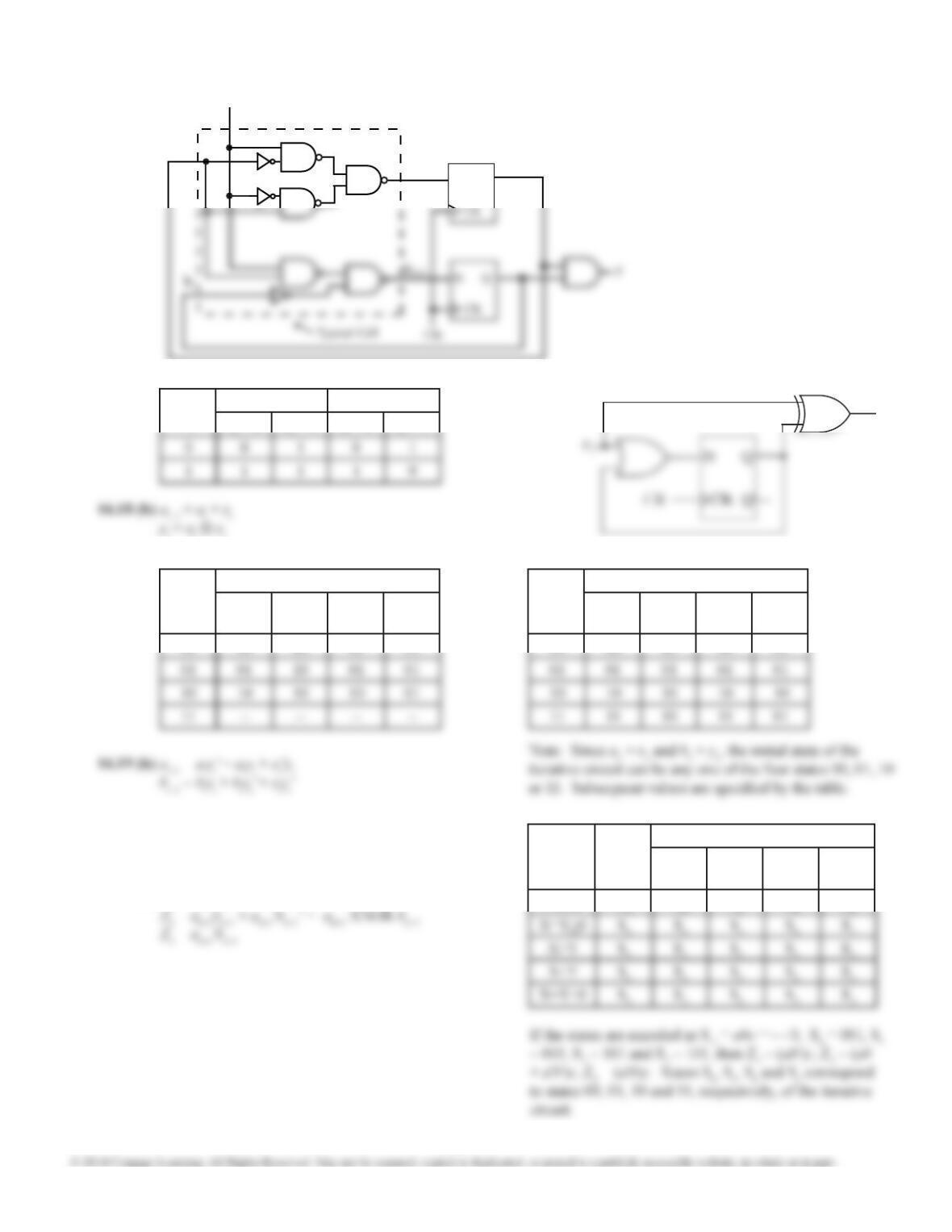
This state machine has too many state variables to use Karnaugh maps. Instead, we will write down equations for
each ip-op by inspection.
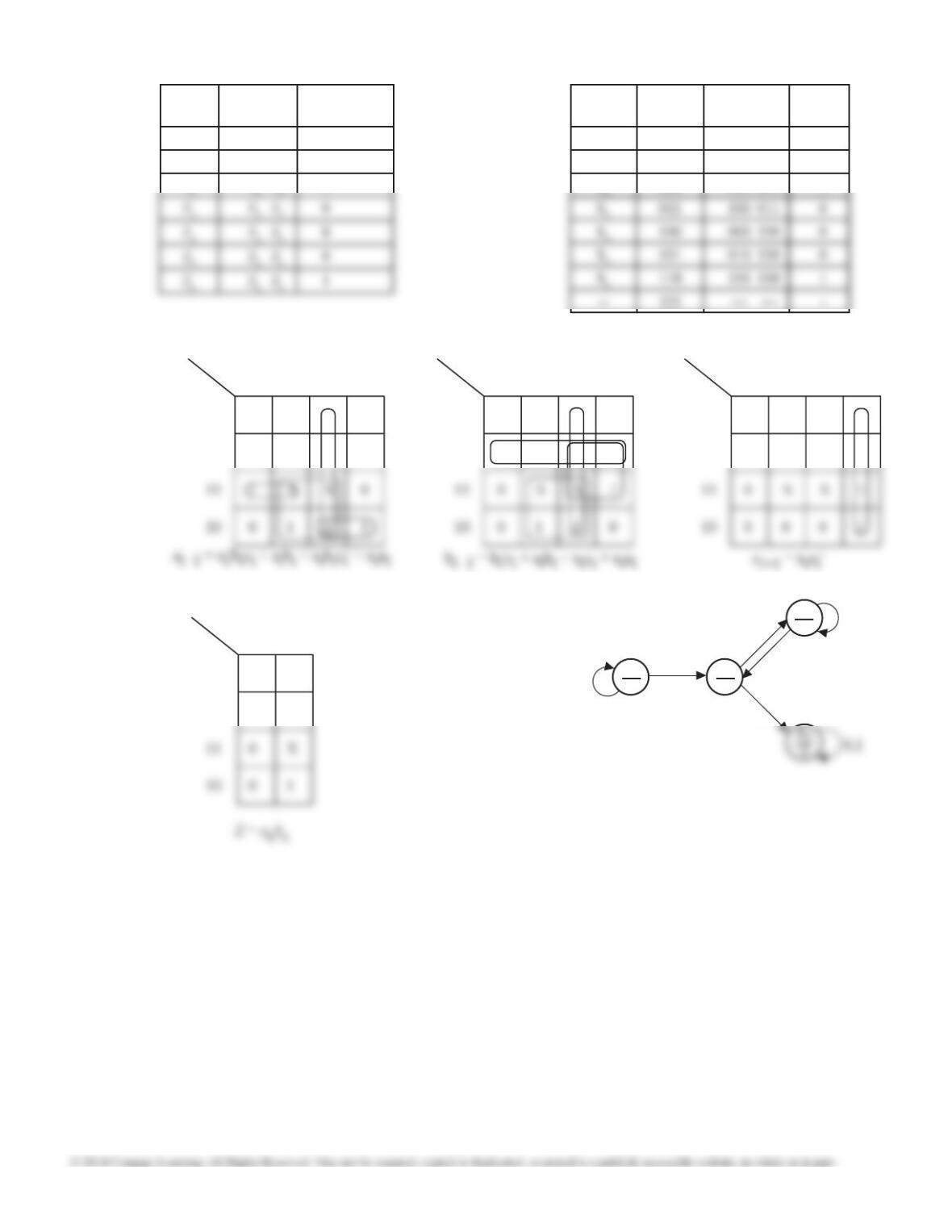
First consider Q1. Q1 = 1 in states S3 or S7 only.
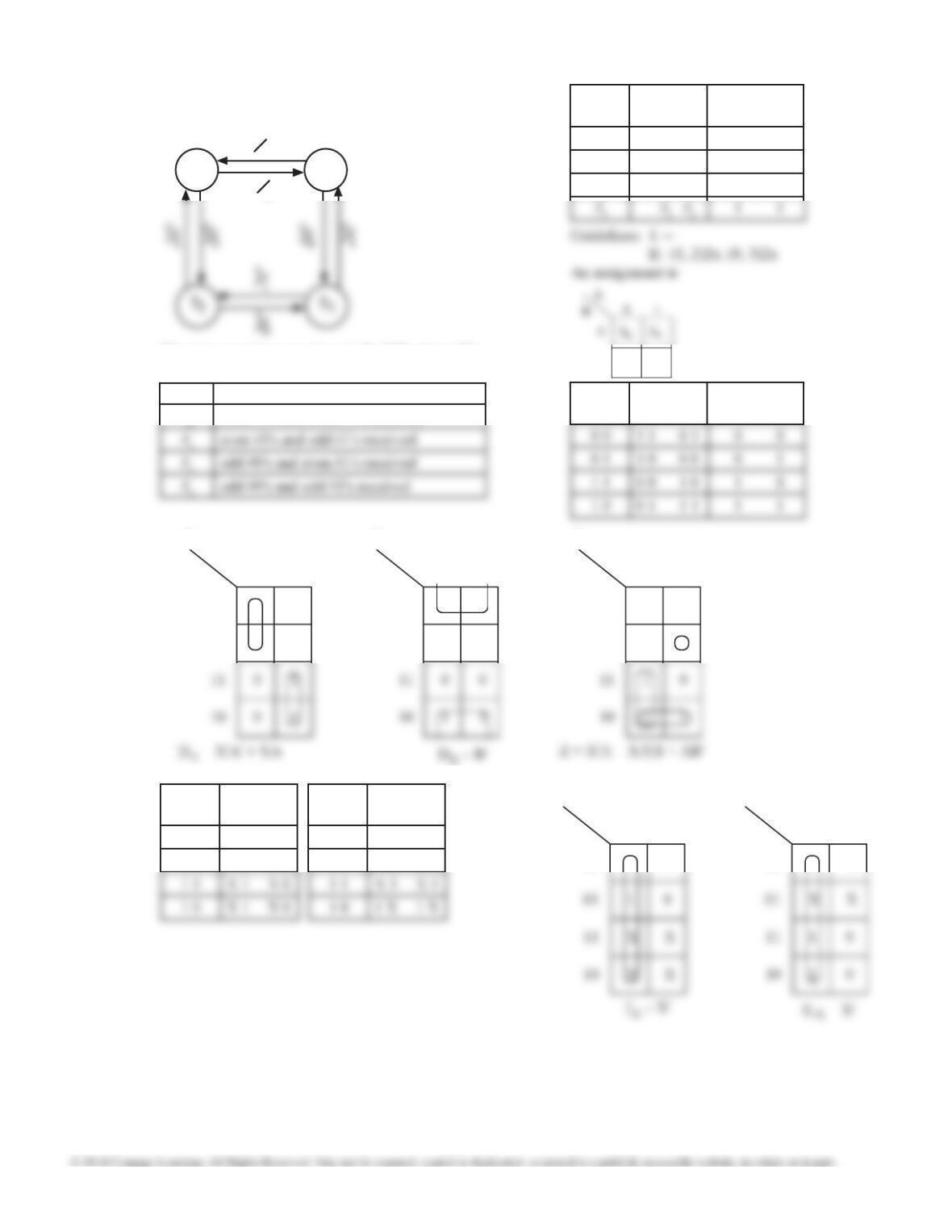
I. (S0, S1, S2, S3, S4, S5, S6) for S7 in LRH = 001, 011, 101
(S1, S2, S3, S6, S7) for S0 in LRH = 010
(S3, S4, S5, S6, S7) for S0 in LRH = 100
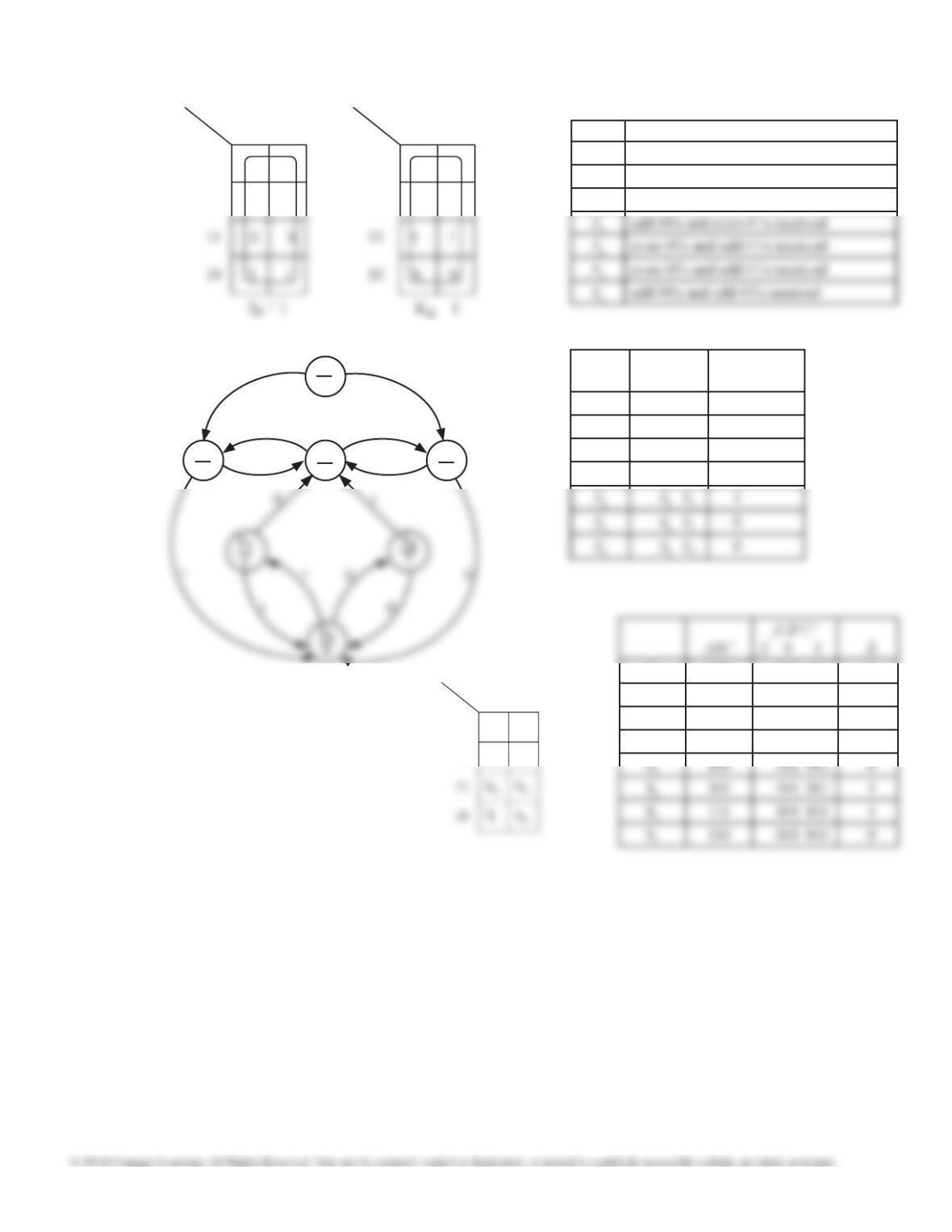
II. Every state matches S0 and S7. But S0 and S7 match the best, so (S0, S7)×(many times)
III. (S1, S2, S3, S7) (S4, S5, S6, S7) etc.
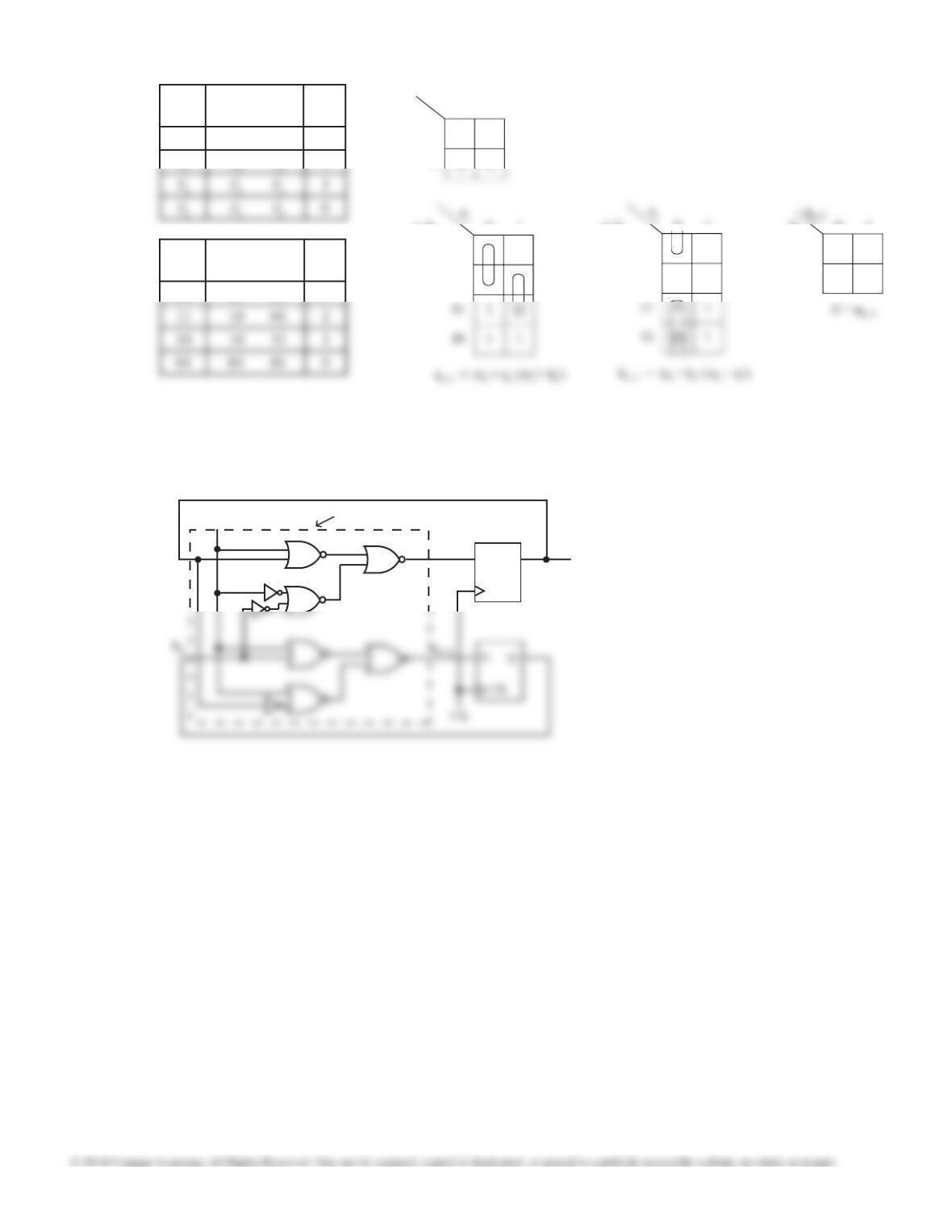
From LogicAid:
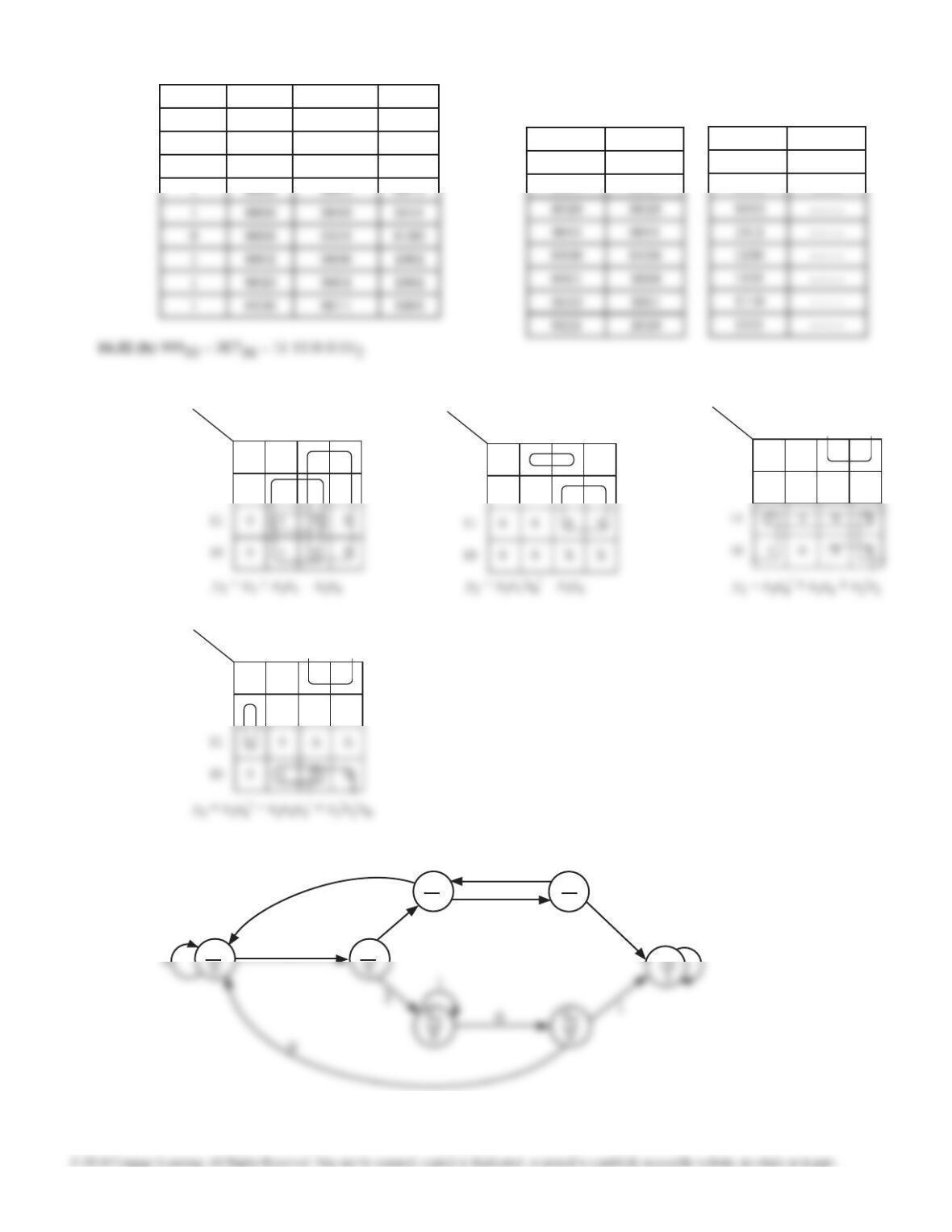
16.30 (c) State LRH = 000 001 010 011 100 101 110 111 LC LB LA RA RB RC
S0 S0 S7 S4 S7 S1 S7 - - 0 0 0 0 0 0
S1 S0 S7 S0 S7 S2 S7 - - 0 0 1 0 0 0
S2 S0 S7 S0 S7 S3 S7 - - 0 1 1 0 0 0
Q1
Q2 Q30 1
00
01
11
S0
S2
S6
S7
S3
S5
211
Unit 16 Solutions
16.31
IDLE
0
RE' FF' PL'
ST, FF ST, RE
RE
FF
PL
ST, FF, RE
Note: This state graph assumes that only one of the buttons ST, PL, RE, and FF can be pressed at any given time.
The graph is incompletely specified and must be augmented before using LogicAid. For example, the arc from REW
to PLAY should be labeled PL ST' FF'.
DQ1
Q1+
ST
RE
FF
PL
M
P
R
F
D1 = ST' FF PS Q1
' Q2
' Q3 + ST' RE PL Q1
' Q2
' Q3
212
Unit 16 Solutions
16.32 (a) 0000 0000 0000
1 0000 0000 0001
1 0000 0000 0011
0 0000 0000 0110
16.32 (c)
x3x2x1x0y3y2y1y0
0000 0000
0001 0001
The tables of combinations for the BCD multiply
by 2 circuit are
x3x2x1x0y3y2y1y0
1000 1011
1001 1100
16.32 (c)
cont.
16.33 (a)
0
S0
S1
S2
0
S6
S4
0
1
1
0
0, 1
1
0
00 01 11 10
00
01
0
0
0
1
1
1
X
X
x0
x1
x3x2
y3
00 01 11 10
00
01
0
0
1
0
0
1
X
X
x0
x1
x3x2
y2
00 01 11 10
00
01
0
0
0
0
1
0
X
X
x3x2
y1
x0
x1
00 01 11 10
00
01
0
1
0
0
1
0
X
X
x0
x1
x3x2
y0
213
Unit 16 Solutions
Present
State
Next State
X = 0 1 Z
S0 S0 S1 0
S1 S2 S3 0
S2 S0 S4 0
ABC
A+B+C+
X = 0 1 Z
S0000 000 001 0
S1001 010 011 0
S2010 000 101 0
16.33 (b)
ai+1 xi ai
bi ci00 01 11 10
00
01
0
0
0
0
0
0
1
1
bi+1 xi ai
bi ci00 01 11 10
00
01
0
1
0
1
0
1
1
1
ci+1 xi ai
bi ci00 01 11 10
00
01
0
0
0
0
1
1
0
0
16.33 (c) Z
an
bn cn0 1
00
01
0
0
0
0
16.34 (a) S2
1
S0
0
S1
1
0
1
1
0
1
0
214
Unit 16 Solutions
DQ
CK
x
i
a
i
a
i+1
Typical Cell
Z
16.34 (c)
16.34 (d)
a1 = b1 = 0
a2 = (x1 + 0)(x1' + 1) = x1
b2 = (x1 + 1)(x1 + 0) = x1
16.34 (b)
ai bi0 1
00
01
0
0
1
0
ai bi0 1
00
01
0
1
1
1
0
0 1
0
10
1
1
bn+1
S0
0 1
0
1S3
S2
S1
ai
bi
State
Next State
xi = 0 xi = 1
Z
S0 S0 S10
S1 S2 S31
aibi
ai+1bi+1
xi = 0 xi = 1
Z
00 00 11 0
