Chapter 15 Many state assignments are not equivalent to the straight

Unit 15 Solutions

177

b c-e

c

d e-h

e-a

c-h

e-a

e h-f

Unit 15 Problem Solutions

15.1 (a)

Reduced state table:

State

Next State

X = 0 X = 1

Output

X = 0 X = 1

A A C1 0

B C F0 0

15.2 a ≡ b

c ≡ e

h ≡ f

d ≡ g ≡ i

See FLD p. 766 for

reduced state table.

15.1 (b)

B

C

D

E

F-H

C-E

C-D

A-F

B-D

A-H

B-E

F-H

A-F

B

C

D

E

F-H

C-E

C-D

A-F

B-D

A-H

B-E

F-H

A-F

Implication chart after one pass: Complete implication chart

A ≡ H

C ≡ E ≡ G

B ≡ D

B ≡ C because F ≡ H, (and also because C ≡ D)

F ≡ H because B ≡ H, (and also because F ≡ G), and

B ≡ H because the output differs for X = 0.

So use the sequence X = 100.

So λ1(B, 100) = 010 ≠ 011 = λ2(G, 100), and B ≡ G.

(Alternative: λ1(B, 110) = 001 ≠ 000 = λ2(G, 110).

Also, λ1(B, 00101) ≡ λ2(G, 00101), but this requires

an X of length 5.

Unit 15 Solutions

178

15.3 S0S5 − a

S1 − b

S5 − a

S1 − c

S1S5 − a

S6 − b

S5 − a

S6 − c

S2S2 − a

S2 − a

S0 ≡ a

S1 ≡ b

a ≡ S0, S5

b ≡ S1

c ≡ S3, S6

Since S2 and S4 do not have corresponding states,

the circuits are not equivalent.

15.3 (a)

15.4 (a) X1 X2

X3 Q 00 01 11 10

00

01

0

1

0

1

00 01 11 10

00

01

X

1

0

1

X

0

X1 X2

X3 Q 00 01 11 10

00

01

0

1

X

1

0

X

X1 X2

X3 Q

The first row may be all 0’s, because if a column has a 1 in the first row, we can invert it so that it has a 0 in the first

row without changing the number of gates. No column should be all 0’s, because that is the same as the two ip-

op case. There are only 3 columns which fit these criteria: 001, 010, and 011. No column may be used twice,

15.5 (a)

15.4 (b)

Excluding 0000, there are 7 possible columns. All possible non-repeating combinations are given below. Those with

repeating rows are crossed out; 29 assignments remain to try.

15.5 (b)

Unit 15 Solutions

179

15.5 (b)

(cont.)

0 0 0

0 1 1

1 0 1

(1 2 3)

0 0 0

0 0 1

0 1 0

1 0 0

(1 2 4)

0 0 0

0 0 1

0 1 0

1 0 1

(1 2 5)

0 0 0

0 0 1

0 1 1

1 0 0

(1 2 6)

0 0 0

0 0 1

0 1 1

1 0 1

(1 2 7)

0 0 0

0 0 1

0 1 0

1 1 0

(1 3 4)

0 0 0

0 0 1

0 1 0

1 1 1

(1 3 5)

0 0 0

0 0 1

0 1 1

1 1 0

(1 3 6)

0 0 0

0 0 1

0 1 1

1 1 1

0 0 0

0 1 1

0 0 0

1 0 1

0 0 0

0 1 1

0 0 1

1 0 0

0 0 0

0 1 1

0 0 1

1 0 1

0 0 0

0 1 1

0 0 1

1 1 0

0 0 0

0 1 1

0 0 1

1 1 1

0 0 0

0 1 1

1 0 1

0 0 0

0 0 1

1 1 0

0 1 0

0 0 0

0 0 1

1 1 0

0 1 1

15.6 (a) Group (S1, S4, S6, S7) and (S2, S3, S5, S8).

One possible assignment:

S1 = 000 S5 = 111

S2 = 100 S6 = 011

S1

A

B C 0 1

00

01

S4

S2

S3

A

B C 0 1

00

01

1

Z = A

15.6 (b) I: (S3, S4) (S1, S8) (S3, S7) (S5, S8)

II: (S4, S5) (S1, S6) (S7, S8) (S1, S7) (S2, S3)

(S2, S4) (S6, S8) (S3, S5)

Adjacencies that are satisfied are checked ()

One possible assignment:

S1 = 000 S5 = 101

X A

B C 00 01 11 10

00

01

11

1

0

1

0

1

0

X A

B C 00 01 11 10

00

01

0

1

0

1

0

1

X A

B C 00 01 11 10

00

01

1

0

1

0

1

0

1

S1

A

B C 0 1

00

01

11

S7

S3

S8

S5

S4

State

ABC

A+B+C+

X = 0 X = 1

S1000 101 111

S7001 110 100

S2010 000 110

S4111 001 000

Unit 15 Solutions

180

15.7 (a) Guidelines:

1. (A, D, F) (C, E) (A, D) (C, E) (B, F)

15.7 (b) See FLD p. 766 for solution.

15.8 (a) Guidelines:

1. (B, D)×2 (C, D)×2 (A, B)

Q

1

Q2

Q

0 1

1

Q2

Q

0 1

1

Q2

Q1 Q2

X1 X200 01 11 10

00

01

0

1

0

1

0

00 01 11 10

00

01

0

1

0

1

Q1 Q2

X1 X2

00 01 11 10

00

01

0

Q1 Q2

X1 X2

00 01 11 10

00

01

0

1

0

1

Q1 Q2

X1 X200 01 11 10

00

01

0

Q1 Q2

X1 X200 01 11 10

00

01

0

1

Q1 Q2

X1 X2

15.8 (b)

15.9 See FLD p. 767 for solution using Q1, Q2, and Q3.

Alternate solution using Q0, Q1 and Q2:

D0 = X’Q0 + XY’Q2

Unit 15 Solutions

181

b

c

d h-f

b-h

15.10 (a)

State

Next State

X = 0 X = 1

Output

X = 0 X = 1

a a c1 0

b c d0 1

c a b0 0

a ≡ g ≡ h

d ≡ f

e ≡ b

Equivalent States: S0 ≡ S8, S3 ≡ S11, S4 ≡ S12,

S7 ≡ S15.

15.12

(a), (b)

15.12 (c)

b d-e

f-g

c

d b-e

f-g 

15.11 (a)

State

Next State

X = 0 X = 1

Output

X = 0 X = 1

a e c0 1

b b f0 1

c e c1 0

b ≡ d

c ≡ g

Input Present Next State Output

Pattern State X = 0 X = 1 Z

-000 S0S0S10

0001 S1S2S30

0010 S2S4S51

-011 S3S6S71

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

-000 S0S0S10 0

0001 S1S2S31 1

0010 S2S4S51 0

-011 S3S6S71 0

-100 S4S0S10 1

Unit 15 Solutions

182

15.12 (d) S1 ≡ S9, S2 ≡ S10, S5 ≡ S13, S6 ≡ S14.

Moore circuit.

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

–S1S2S30 0

0S2S4S50 0

1S3S6S70 0

15.13 (a)

15.13

(b), (c)

S8 ≡ S9 ≡ S10 ≡ S11 ≡ S12

and S13 ≡ S14 ≡ S15.

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

–S1S2S30 0

0S2S4S40 0

1S3S6S70 0

S4 ≡ S5.

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

–S1S2S30 0

0S2S4S50 0

000 S8S1S10 0

001 S9S1S10 1

010 S10 S1S10 1

011 S11 S1S10 1

15.14 (a) 15.14

(b), (c)

S9 ≡ S10 ≡ S11 ≡ S13 ≡ S14 ≡ S15

and S8 ≡ S12.

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

10 S6S8S90 0

11 S7S9S90 0

-00 S8S1S10 0

-01, -1- S9S1S10 1

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

-000 S0S0S10 0

-001 S1S2S31 1

-010 S2S4S51 0

Unit 15 Solutions

183

15.14(b),

(c)

(cont.)

Equivalent States: S4 ≡ S6 and S5 ≡ S7.

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

–S1S2S30 0

0S2S4S50 0

1S3S4S50 0

Equivalent States: S2 ≡ S3.

Input Present Next State Output Z

Pattern State X = 0 X = 1 X = 0 X = 1

–S1S2S20 0

–S2S4S50 0

-0 S4S8S90 0

b a-d

c-e

c

d a-b

e-c

b-d

e-c

a-b

15.15 (a)

a ≡ b ≡ d

c ≡ e

Present

State

Next State

00 01 11 10

Z

a a c c a0

c c a f a1

f f a a a1

15.15 (b)

State

Next State

X = 0 X = 1

Z

X = 0 X = 1

a b c 1 0

b e b 1 0

c g b 1 1

b b-e

c-d

c

d b-e

b-c

b-d

e b-f

e-f

i a-h

a-i

g-a

i-a

a b c d e f g h

b ≡ d

g ≡ h

c ≡ f

Unit 15 Solutions

184

b

c a-g, a-c

k-i

d k-i g-a

c-d

h a-g, a-h

g-d

a-d

i-k

a-g, d-h

g-d, i-k

c-h

i c-h

f-h

a-d

15.16 (a)

a ≡ d ≡ j

b ≡ e ≡ i ≡ k

c ≡ f ≡ h

b i-c

c-f

c

d d-c, d-e

f-g

h b-e

i-f

b-e

c-f

b-e, c-f

i-c

f-e, i-f

i-c, k-g

j-e, k-f

h-g, g-c

i b-i, c-i

g-d

b-i, c-i

f-i, g-d

b-i, c-i

g-d

k-d j-i, k-i

g-i, h-d

e-i, f-i

c-i, g-d

a ≡ h ≡ j

b ≡ e

d ≡ k

Present

State

Next State

g a d g a0

15.16 (b)

Unit 15 Solutions

185

S0 ≡ e ≡ f, S1 ≡ c ≡ d, S2 ≡ S3 ≡ a ≡ b

Since every state in N has an equivalent state in M, and

vice versa, N and M are equivalent.

S0E − S3

D − S1

E − S3

C − S1

B − S3

D − S1

B − S3

C − S1

15.17 (a) M

X = 0 1

S0 S2 S10

S1 S0 S10

S2 S0 S21

15.17 (b) N

X = 0 1

A E A1

C E C0

E A C0

Set don’t care to S3 so S4 ≡ S3:

Present

State

Next State

X = 0 1

Output

S0 S1 S00

15.18 (a)

Set don’t care to S2 so S4 ≡ S1:

Present

State

Next State

X = 0 1

Output

S1

S0S1 − S1

1

S0 − S0

1

S1 − S0

1

S0 − S2

1

S1 − S0

1

S0 − S3

1

S1S0 − S1

1

S0 − S0

1

S0 − S0

1

S0

1S1

1S2

1S3

1

S2 and S2

1 have no corresponding states,

∴ N and N’ are not equivalent.

15.18 (b)

Set don’t care to 0 so S2 ≡ S4 ≡ S5:

Present

State

Next State

X = 0 1

Output

X = 0 X = 1

S0 S1 S2 0 0

15.19 (a) Set don’t care to 0 so S1 ≡ S3 ≡ S4:

Present

State

Next State

X = 0 1

Output

X = 0 X = 1

S1

0 S1

1 S1

5 0 0

15.19 (b) S0S1 − S1

1

S2 − S1

5

S1S3 − S1

1

S2 − S1

2

15.19 (c) X = 1 0

Z = 0 1

Z1 = 0 0

Unit 15 Solutions

186

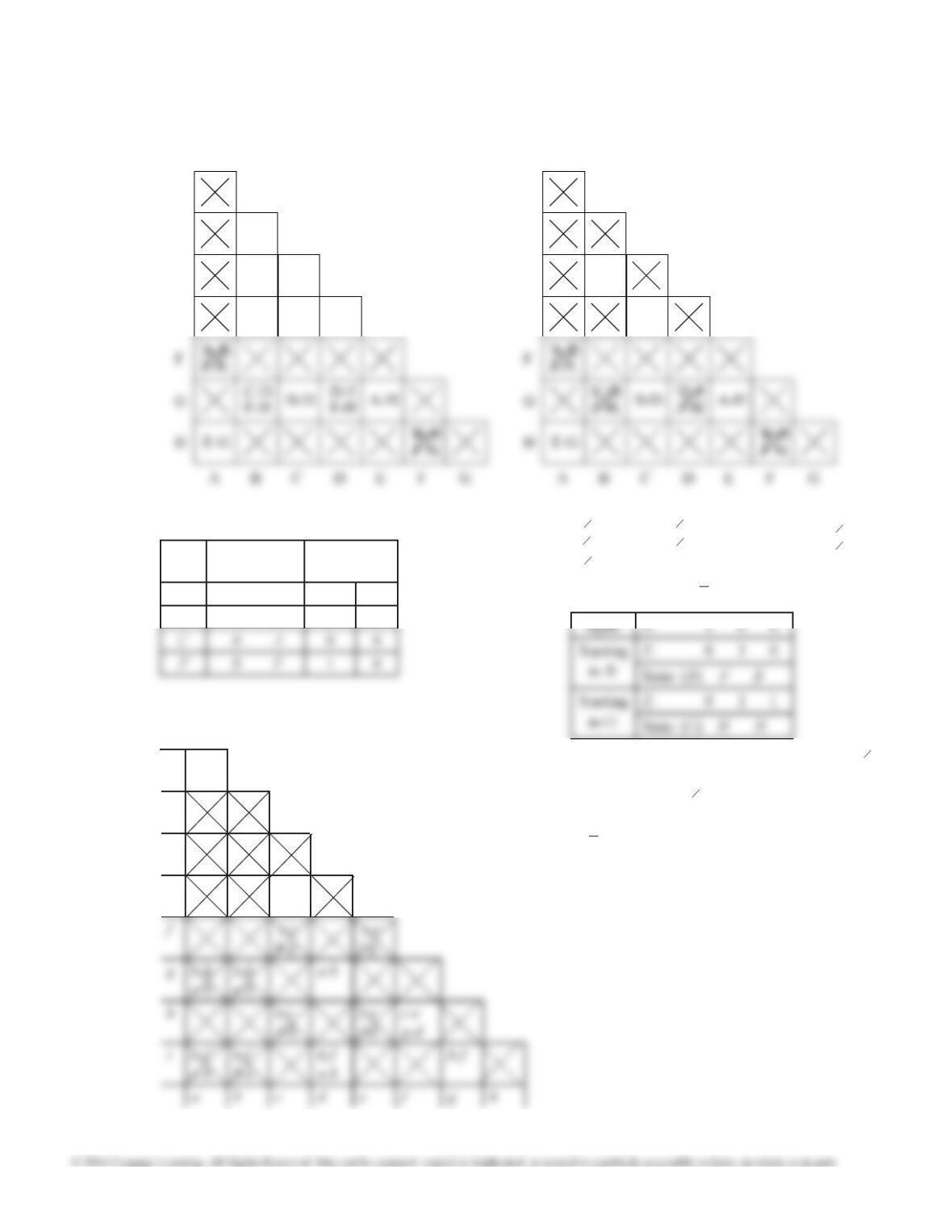
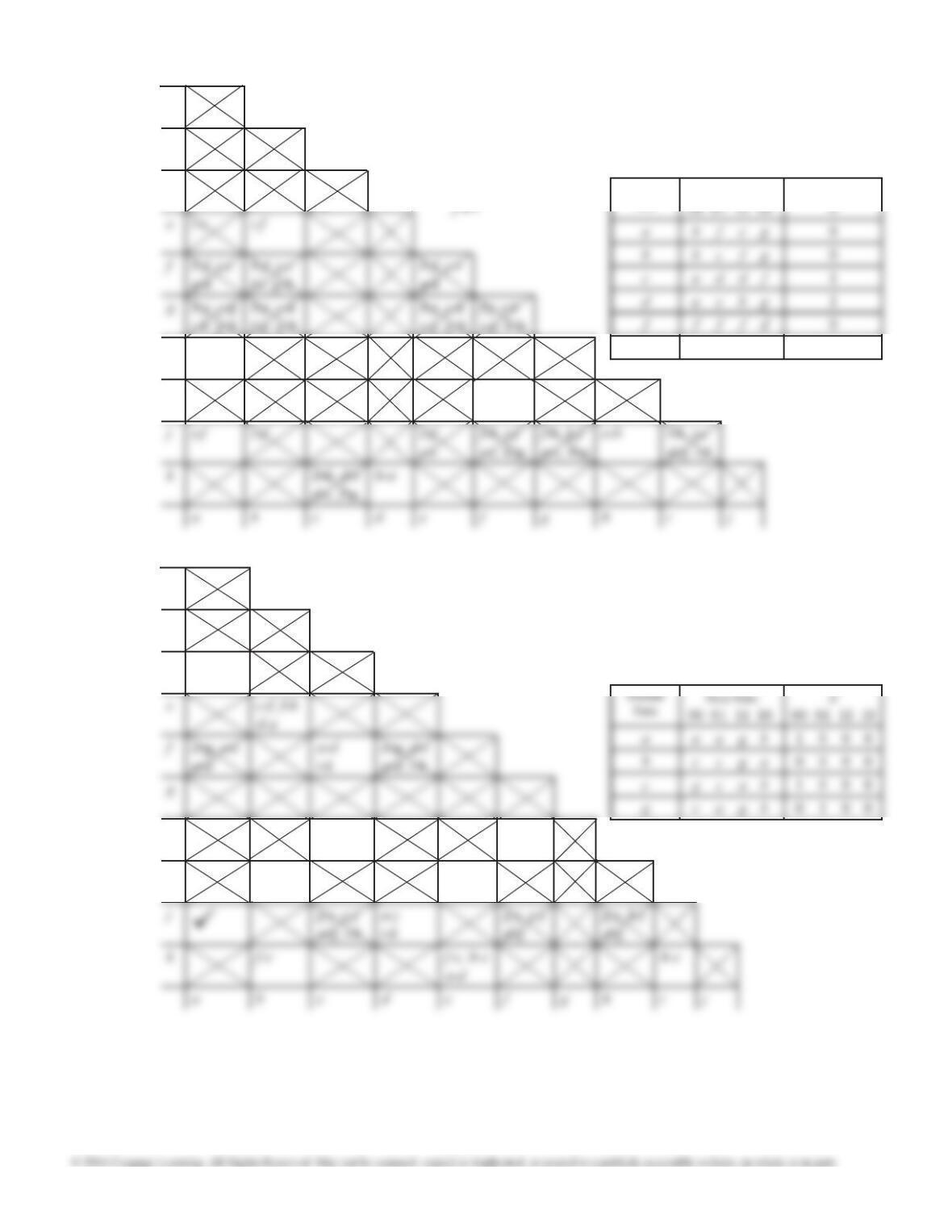
15.21 (b) Many state assignments are not equivalent to the

straight binary assignment, for example:

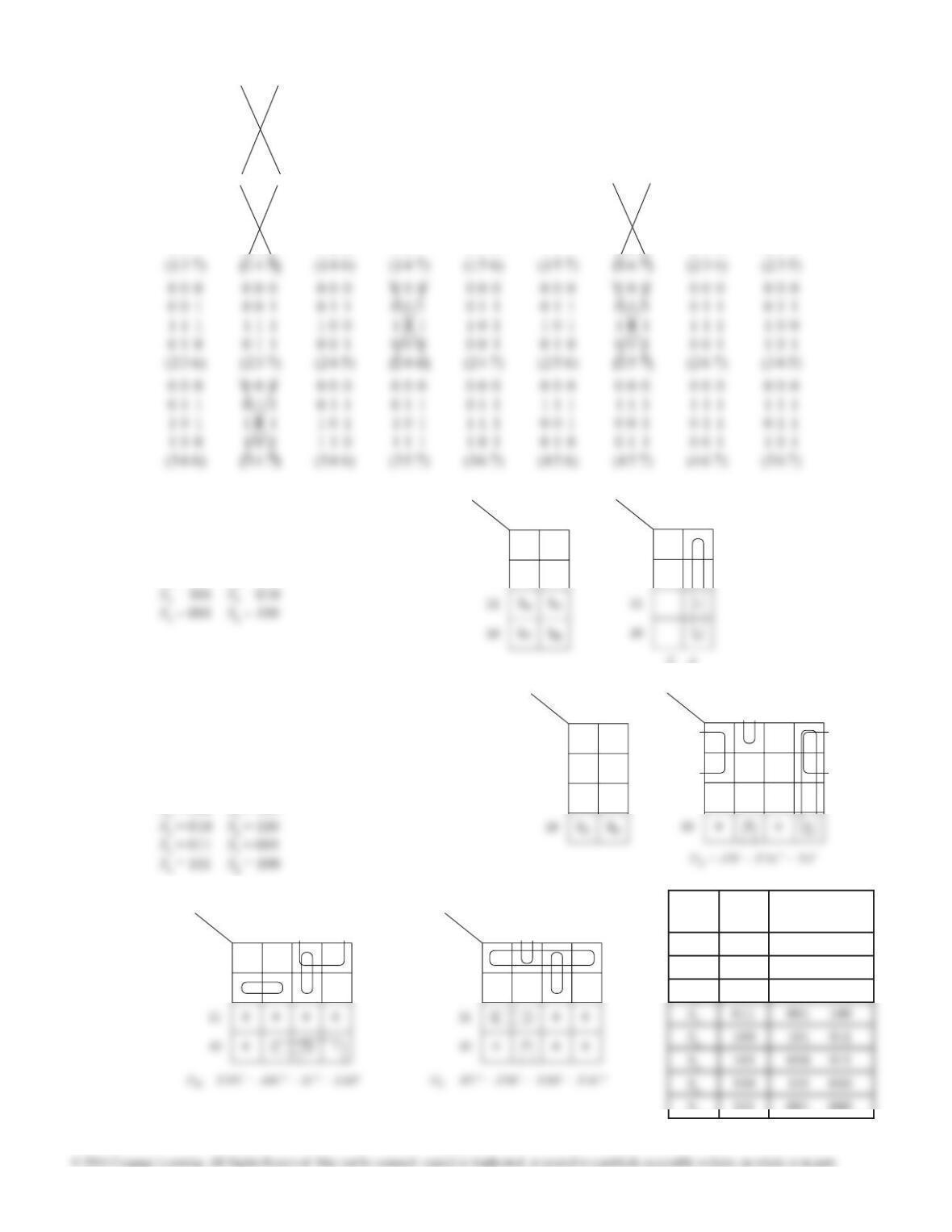
15.20 (a) Invert all three columns of assignment (iv), and

then swap the first and last columns. Then (iii)

and (iv) are the same, therefore, Assignment (iii) ≡

Assignment (iv).

15.20 (b) Equivalent assignments to each column having 000

as the starting state. Invert any column with 1 in

the first row.

(ii) – (c’

2)iii – c’

1iv – c’

1c’

2v – c’

3

S0000 000 000 000

S1101 001 100 110

S2011 100 001 100

S3100 101 101 010

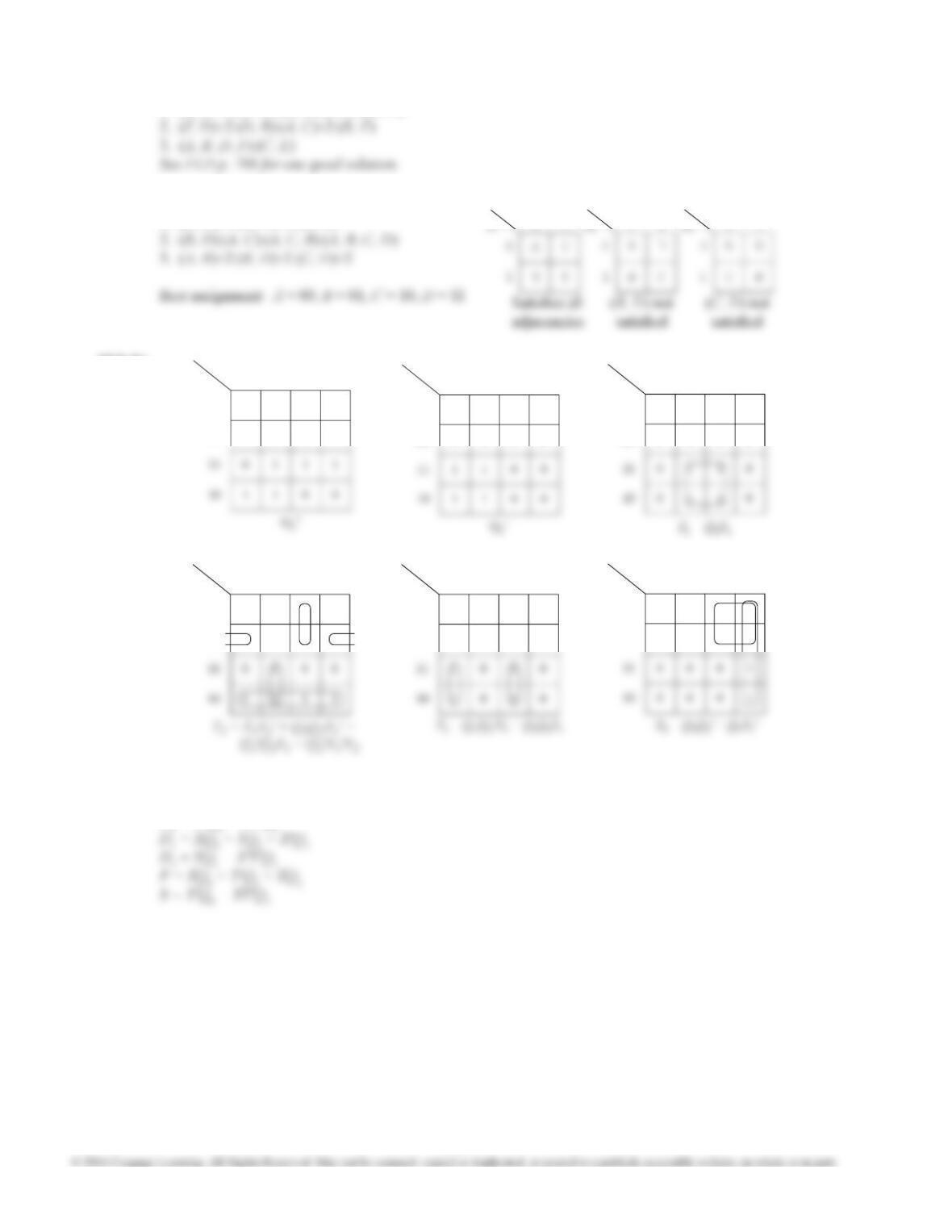
15.20 (c) Many state assignments are not equivalent to

(i) through (v), for example:

101 or 011

000 101

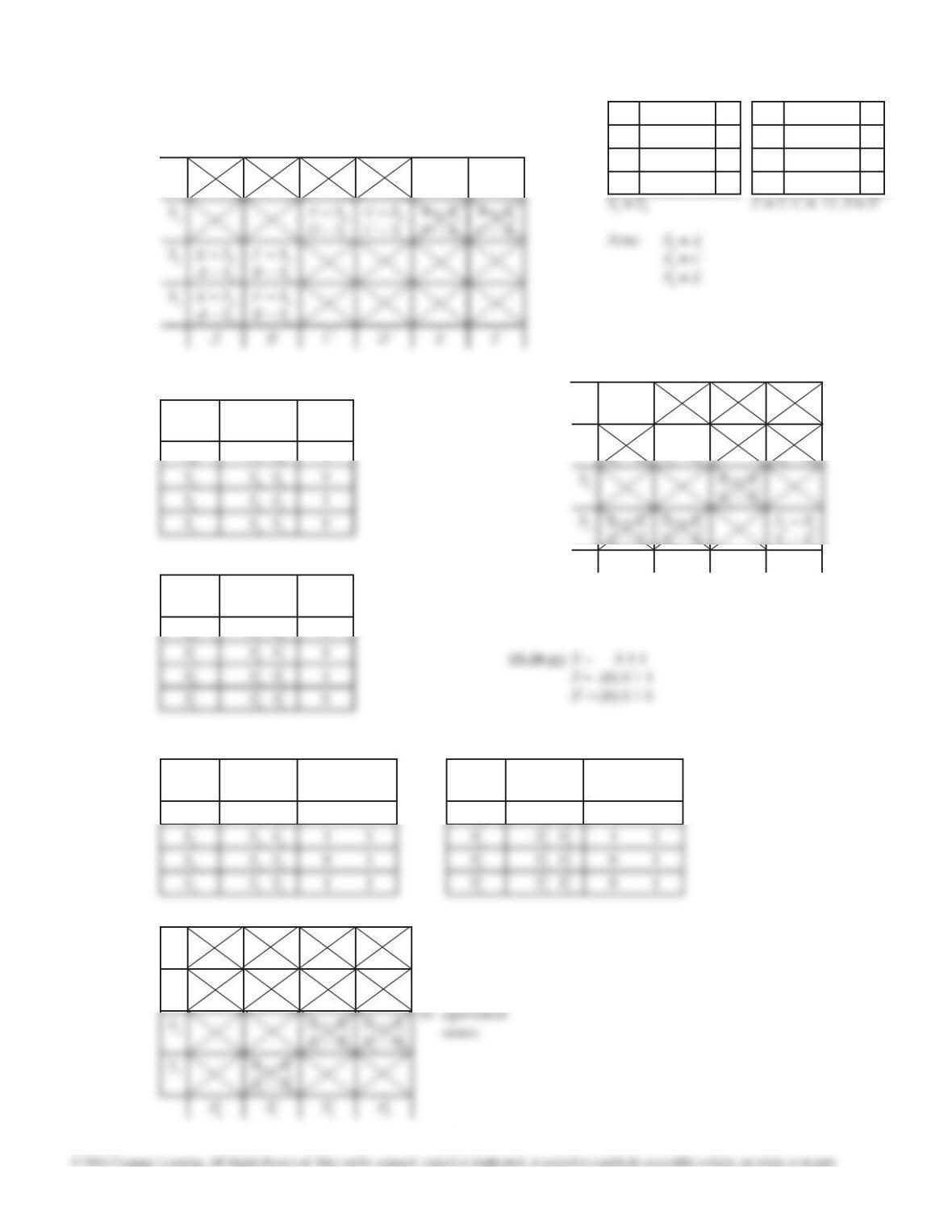
15.21 (a) Straight

Binary

Assignment

Equivalent State Assignments (any three)

c2 ↔ c3c1 ↔ c3c1 ↔ c2c1 → c3→ c2→ c1c1 → c2→ c3→ c1

000 000 000 000 000 000

001 001 100 010 010 100

111 111 etc.

101 001

110 010

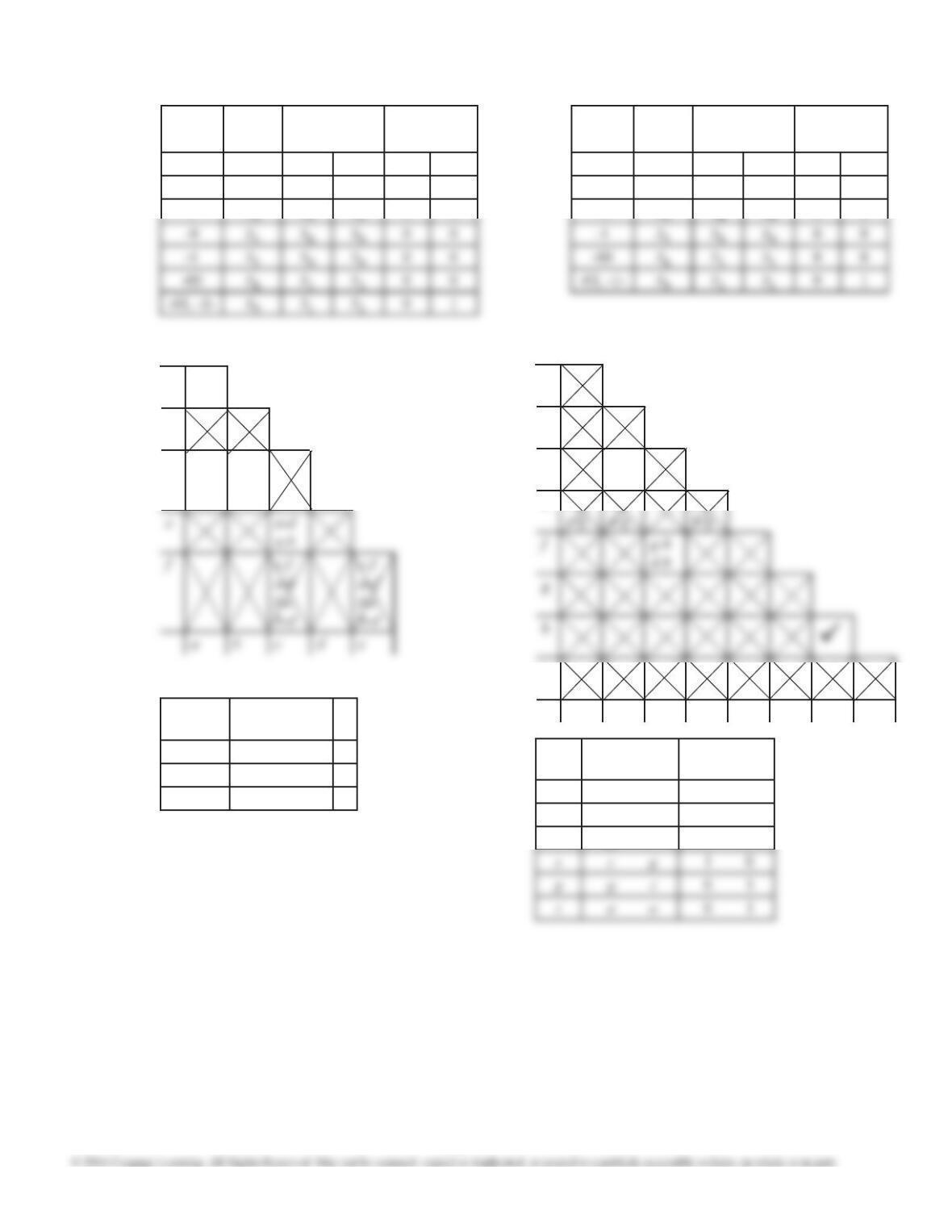
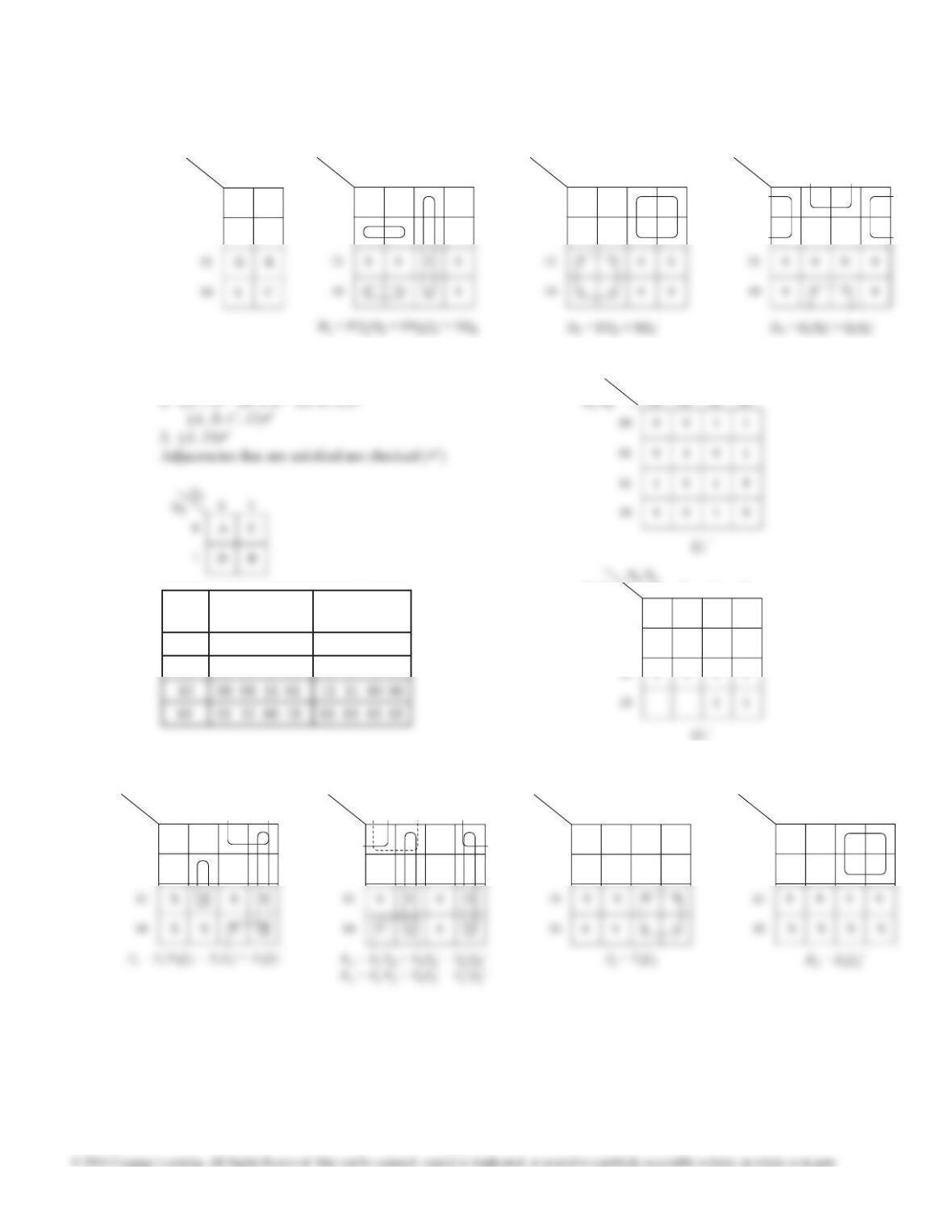
15.22 (a) 1. (A, H) (B, G) (A, D) (E, G)

2. (D, G) (E, H) (B, F) (F, G ) (C, A) (H, C) (E, A)

Q

1

0 1

Q1

Q2 Q3

Unit 15 Solutions

187

15.22 (b)

A

0 1

00

01

D

H

F

Q1

Q2 Q3

X Q1

Q2 Q300 01 11 10

00

01

0

1

0

1

0

1

X Q1

Q2 Q300 01 11 10

00

01

0

1

X Q1

Q2 Q300 01 11 10

00

01

1

0

1

0

15.23 (a) 1. (A, C)×2 (B, C)×2 (A, D)

Q1Q2

Q1

+Q2

+

00 01 11 10

Z1Z2

00 01 11 10

00 00 00 10 10 01 01 01 01

11 11 01 11 01 11 11 11 11

X1 X2

Q1 Q200 01 11 10

00

01

0

1

0

00 01 11 10

00

01

0

X

0

X

0

X

0

X

X1 X2

Q1 Q2

00 01 11 10

00

01

X

X1 X2

Q1 Q200 01 11 10

00

01

X

0

X

0

X

1

X

1

X1 X2

Q1 Q2

X1 X2

00 01 11 10

00

01

1

Q1 Q2

15.23 (b)

(cont.)

Consider Guidelines #1, 2:

A = 000, B = 111, C = 110, D = 001, E = 010,

F = 101, G = 011, H = 100

Unit 15 Solutions

15.25 (a) B

C A-F

B-G

D E-A

A ≡ F ≡ H

B ≡ I

D ≡ G

1. (A, C) (B, D) (C, E)

2. (A, B) (C, E) (A, D) (A, C) (B, D)

3. (A, C, E) (B, D)

Adjacencies that are satisfied are checked ()

A = 000, B = 100, C = 001, D = 101, E = 011

All are satisfied except (A, D)

Alternate:

Q1Q2Q3

Q1

+Q2

+Q3

+

X = 0 1

Z

000 000 100 1

15.25 (b)

15.25 (c)

State

Next State

X = 0 X = 1

X

A A B1

B C E0

15.24 (a)

Guidelines:

1. (A, D)x2 (C, E) (A, B, D, E)

2. (A, B)x2 (A, C) (D, E) (A, E)

The following assignment satisfies all but (A, E),

(A, C) and (B, D):

Q1Q2Q3

Q1

+Q2

+Q3

+

X = 0 1

z

000 001 000 0

010 111 000 0

011 011 000 0

Equations for one-hot state assignment:

15.24 (b)