174
Unit 14 Solutions
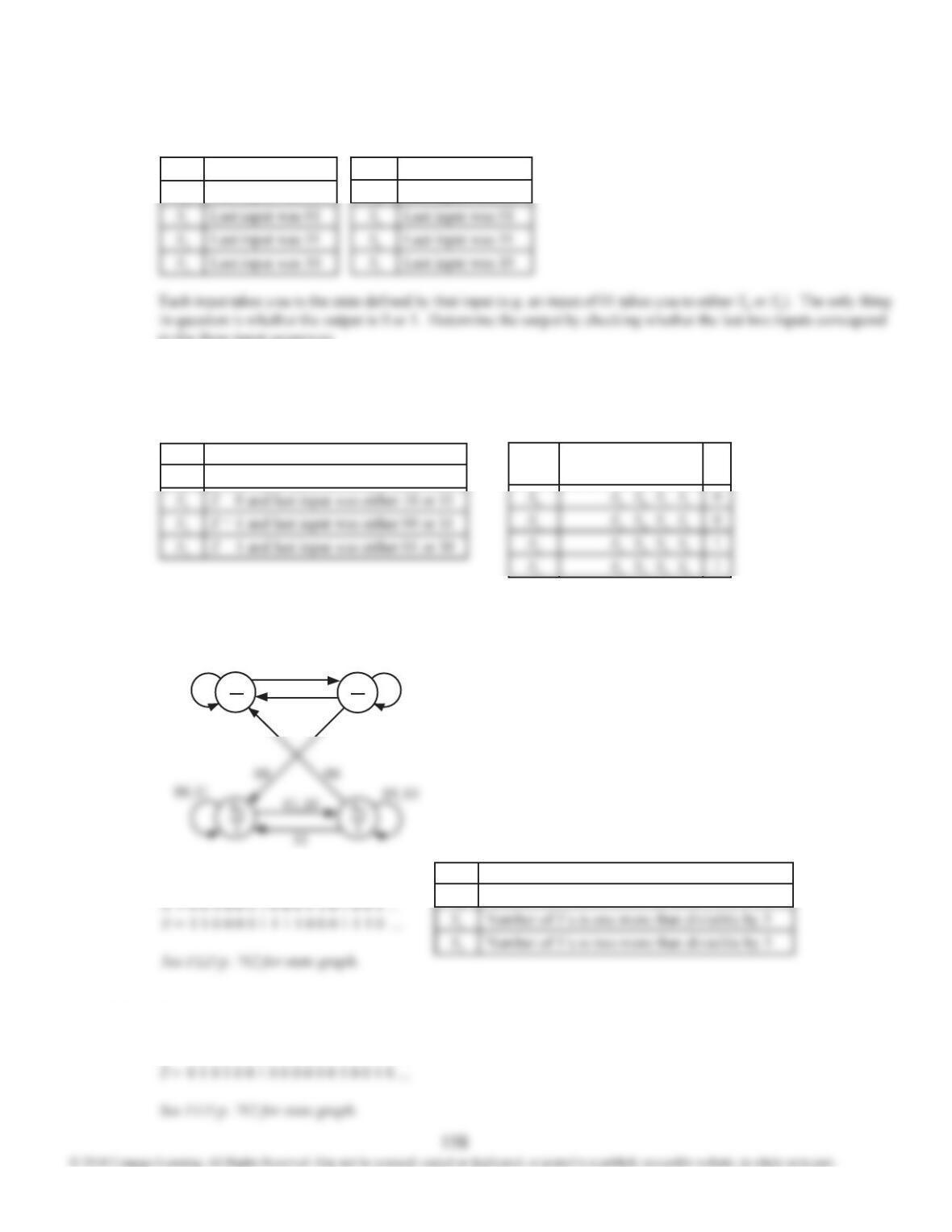
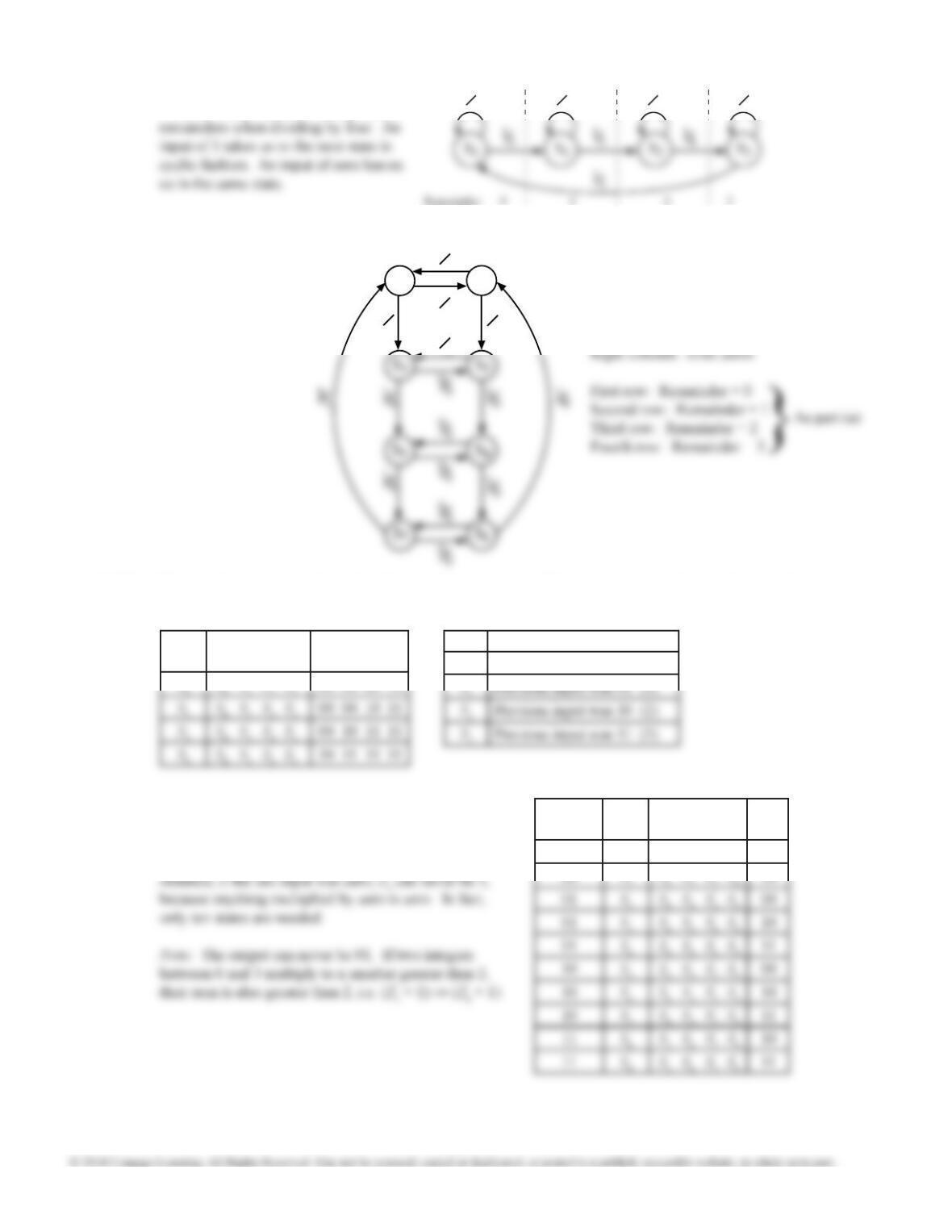
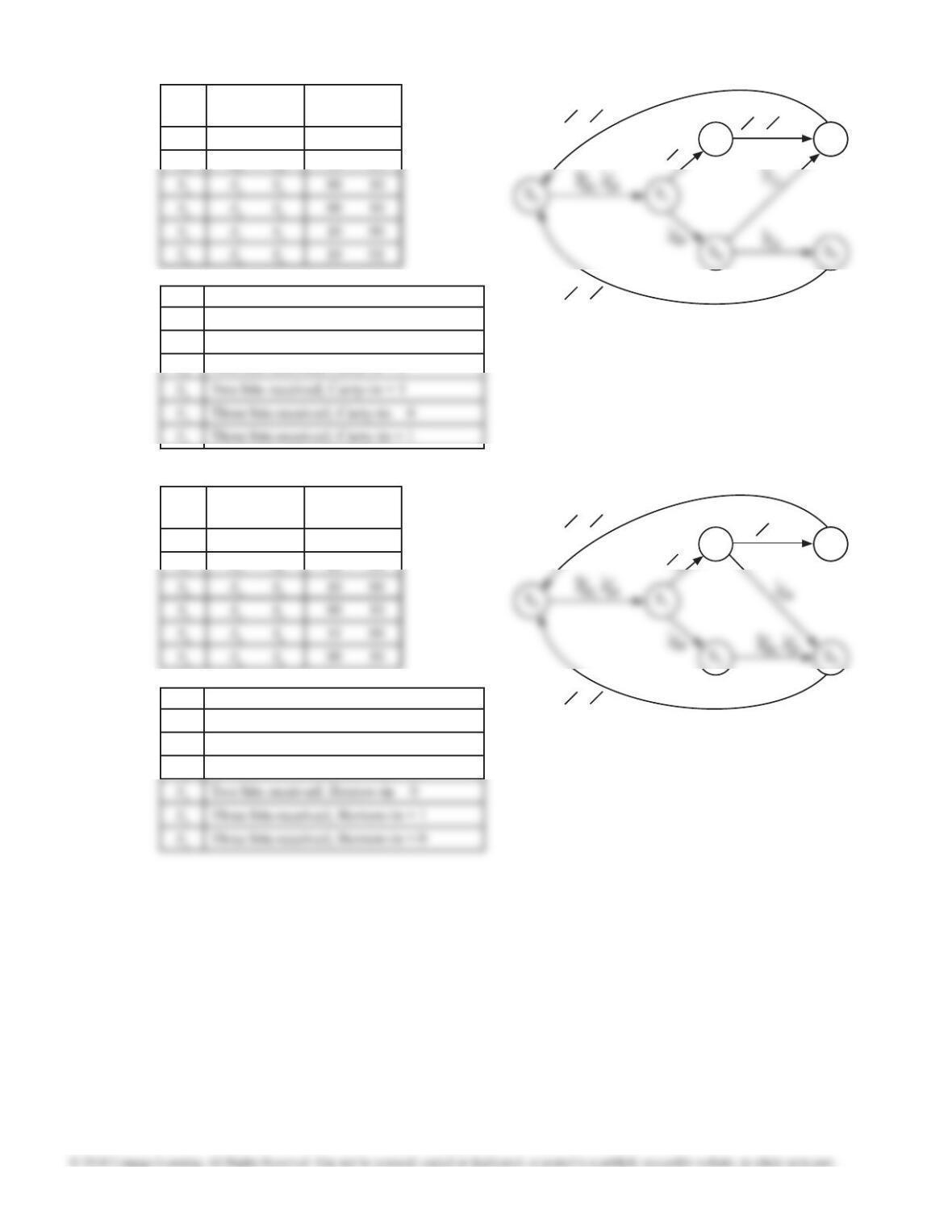
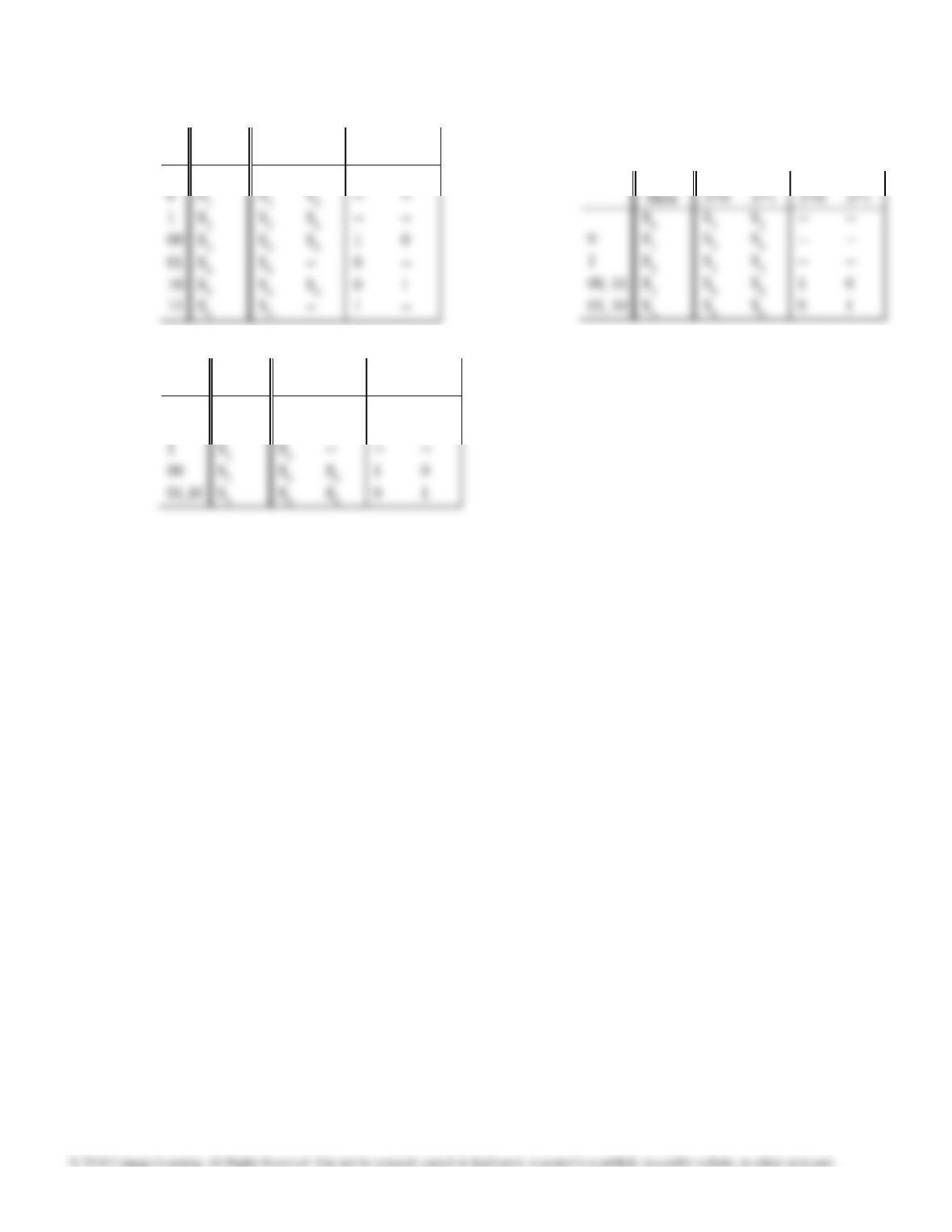
14.47
State
X = 0
X = 1
X =0
X = 1
1
3
4
2
5
6
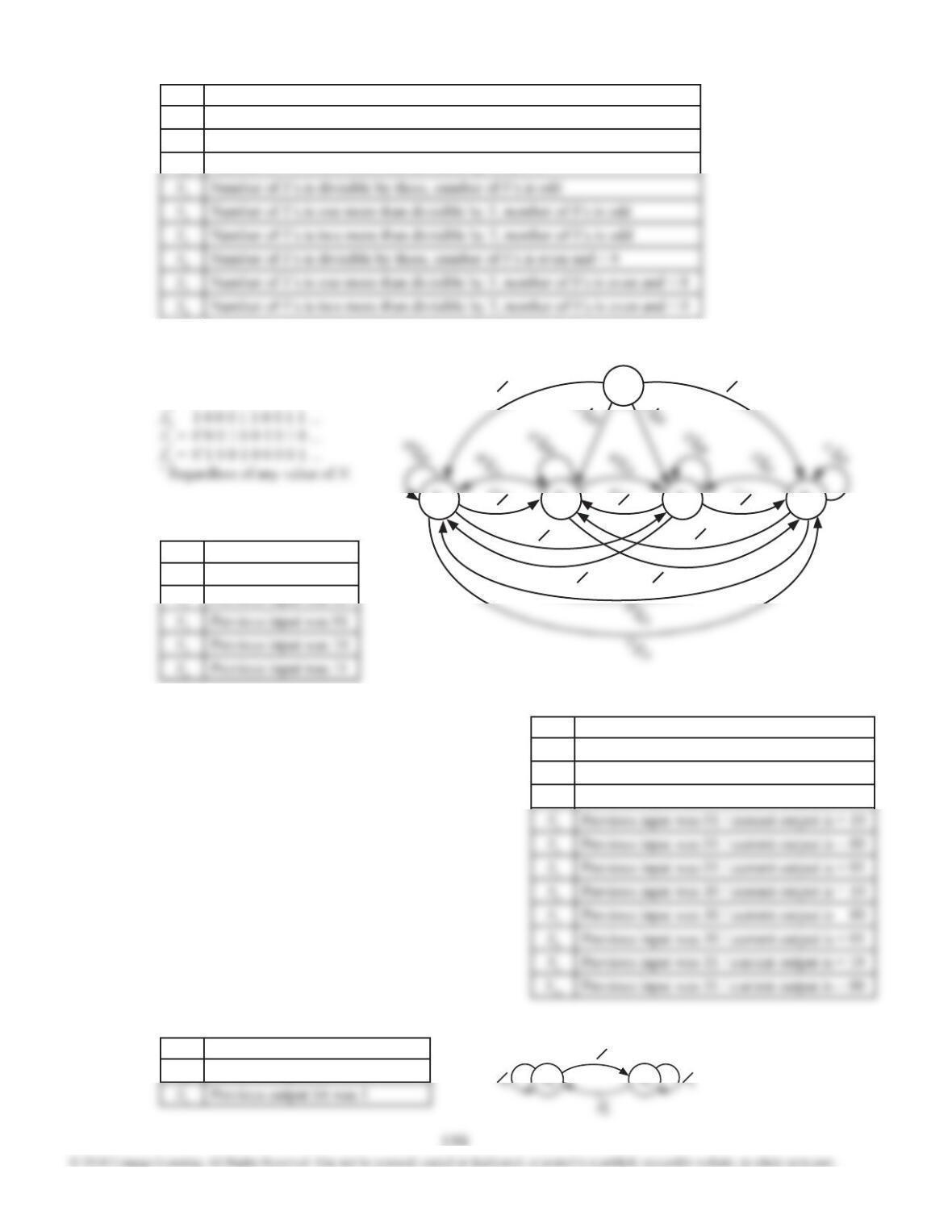
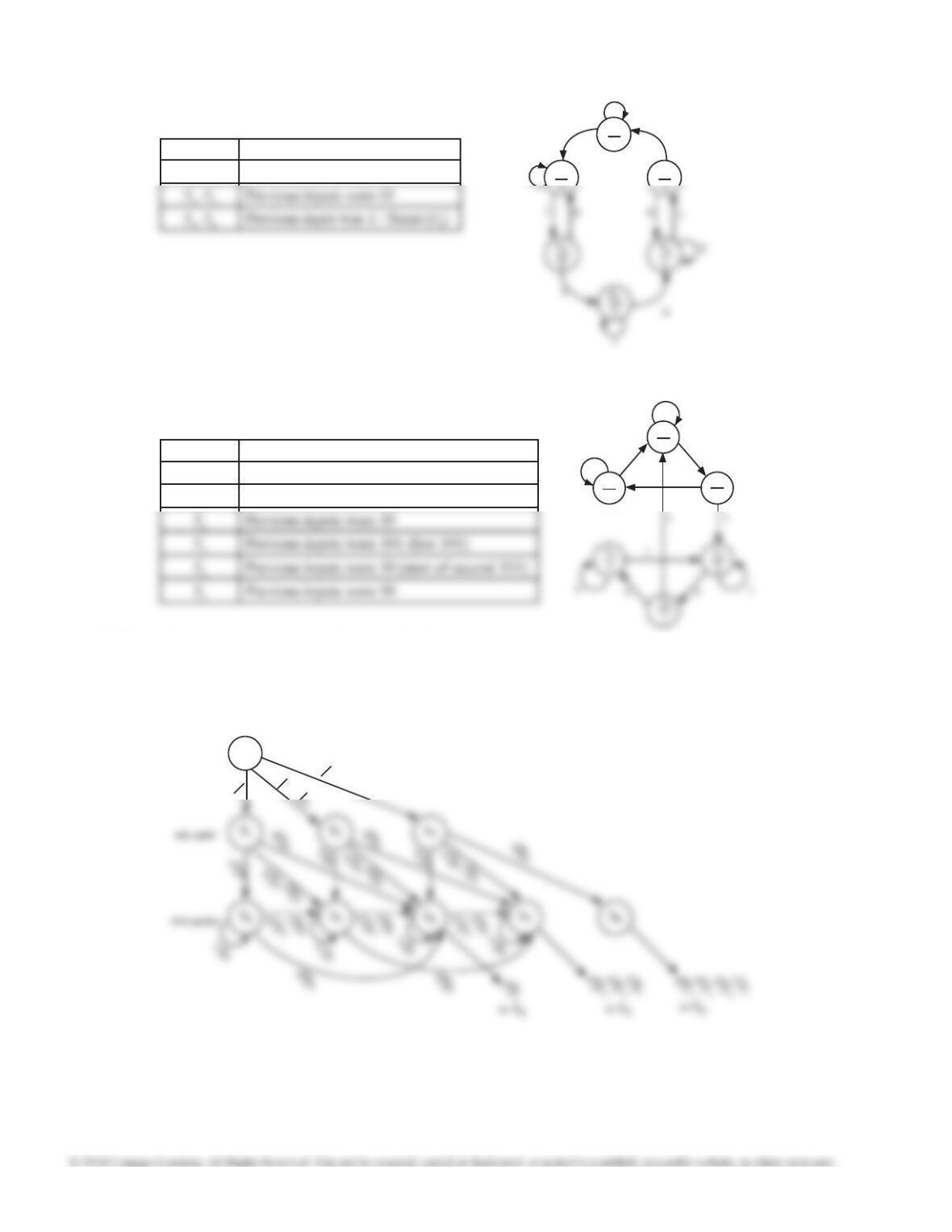
14.48
State
X = 0
X = 1
X =0
X = 1
1
3
4
14.49
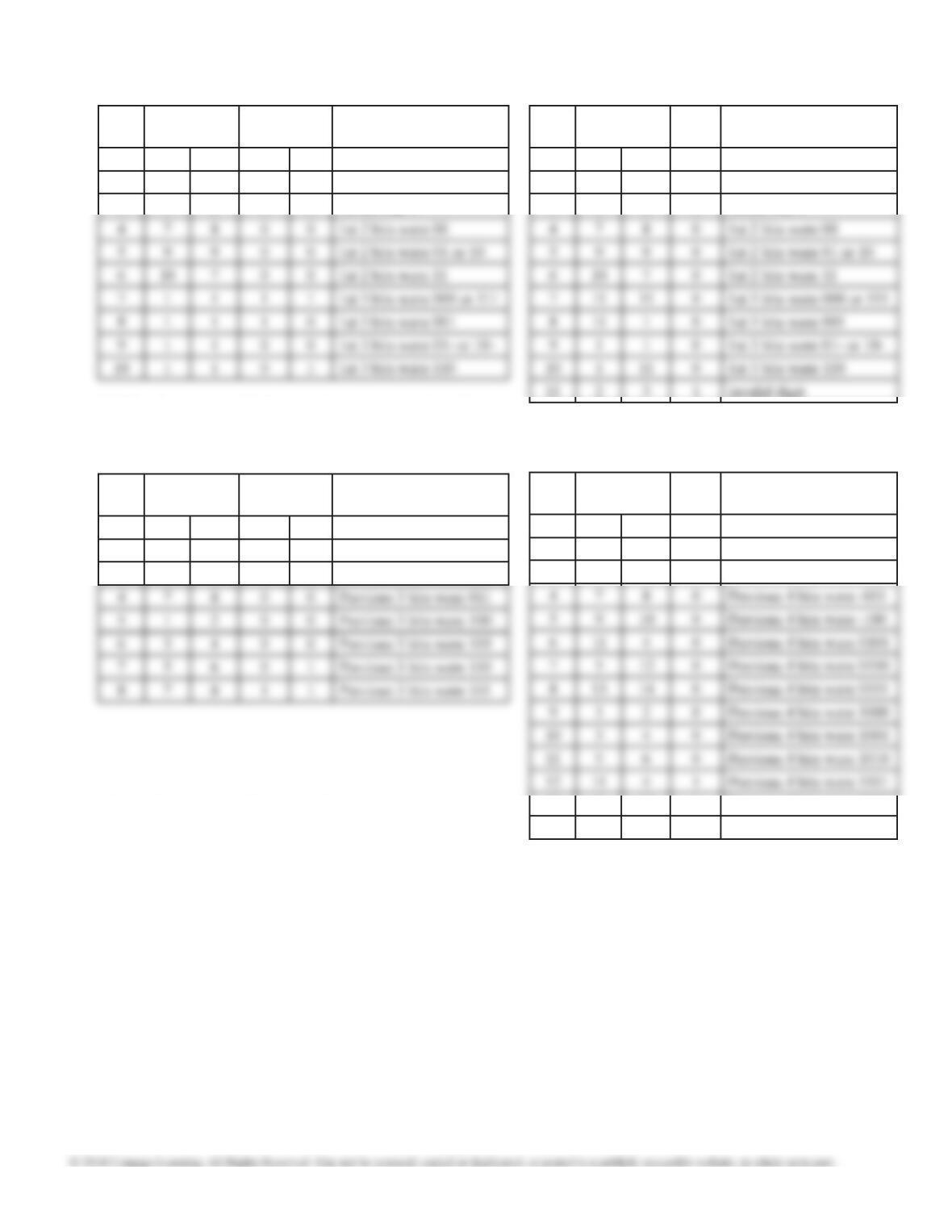
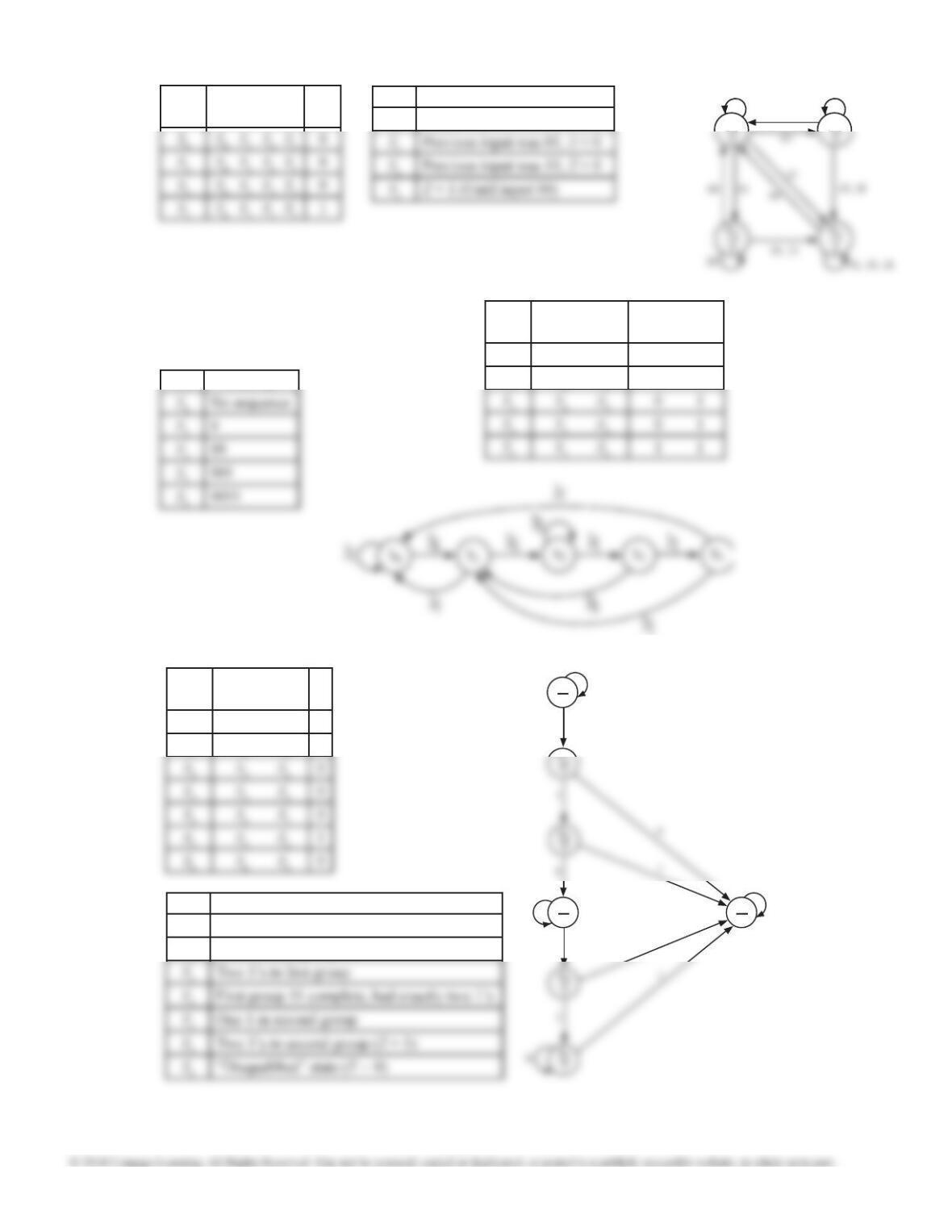
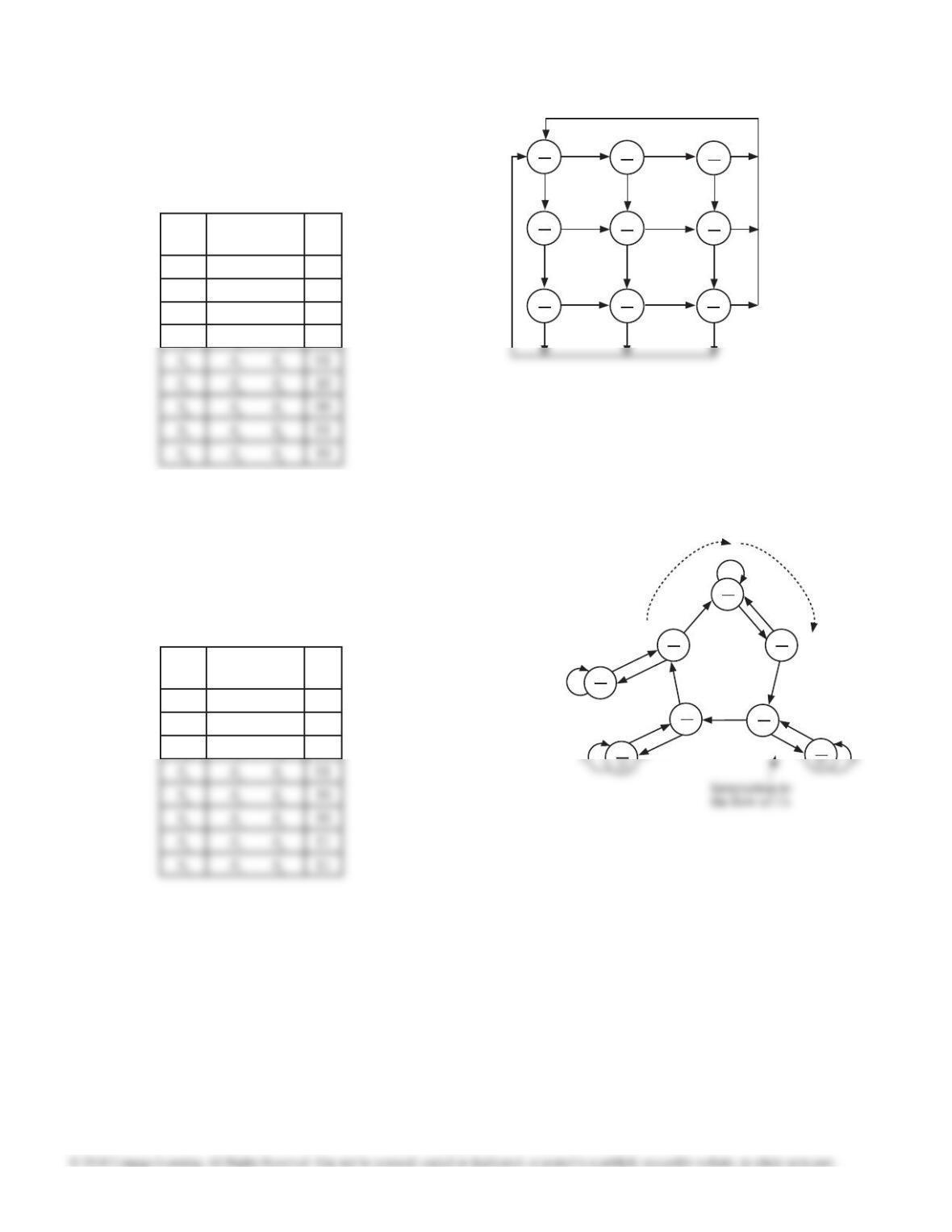
State
X = 0
X = 1
X =0
X = 1
1
3
4
Noting that the six illegal sequences only need to
be distinguished by their parity produces this table.
This table can be reduced using techniques of Unit
15. Alternatively, it can be reduced by noting that
all sequences of length 2 and all of length 3 only
need to be distinguished by their parity.
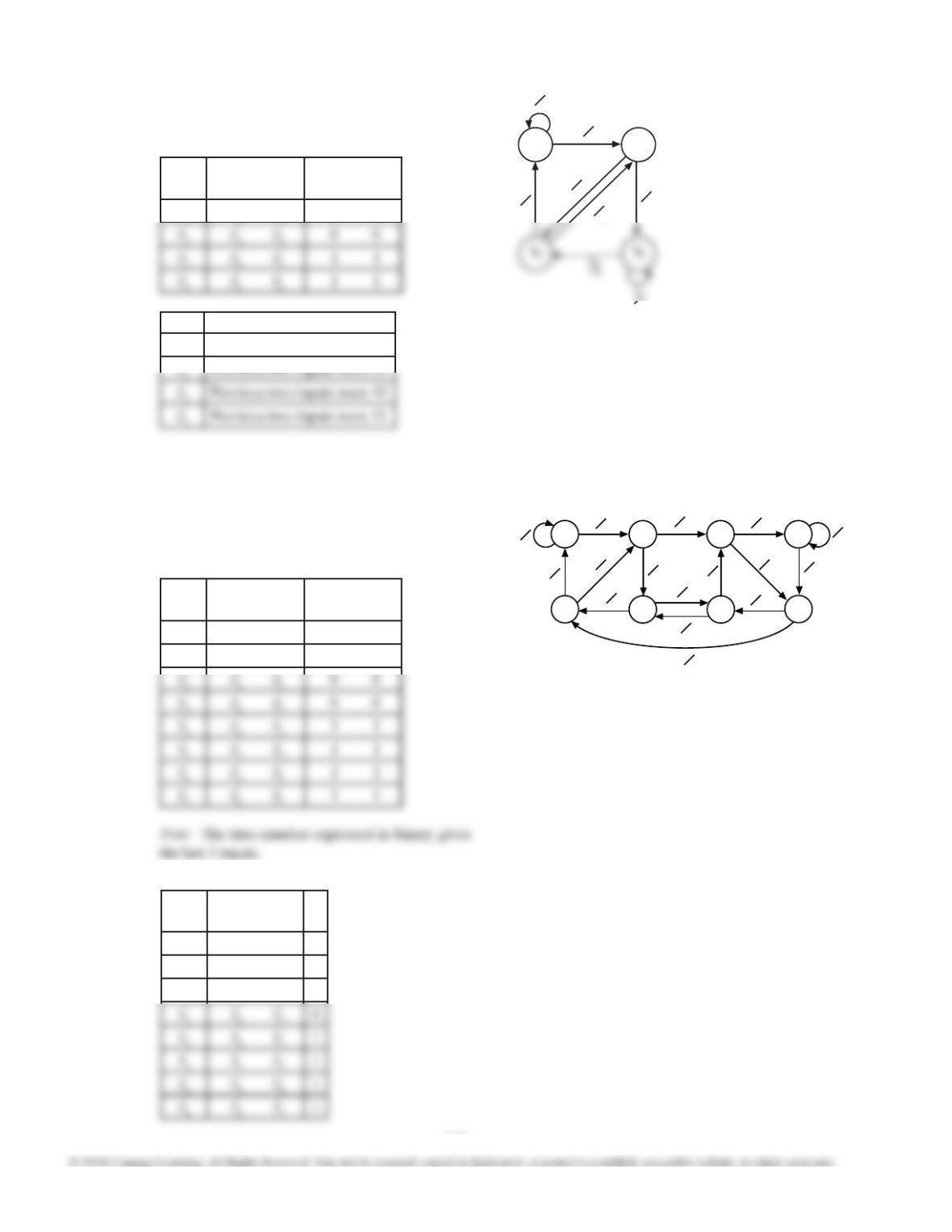
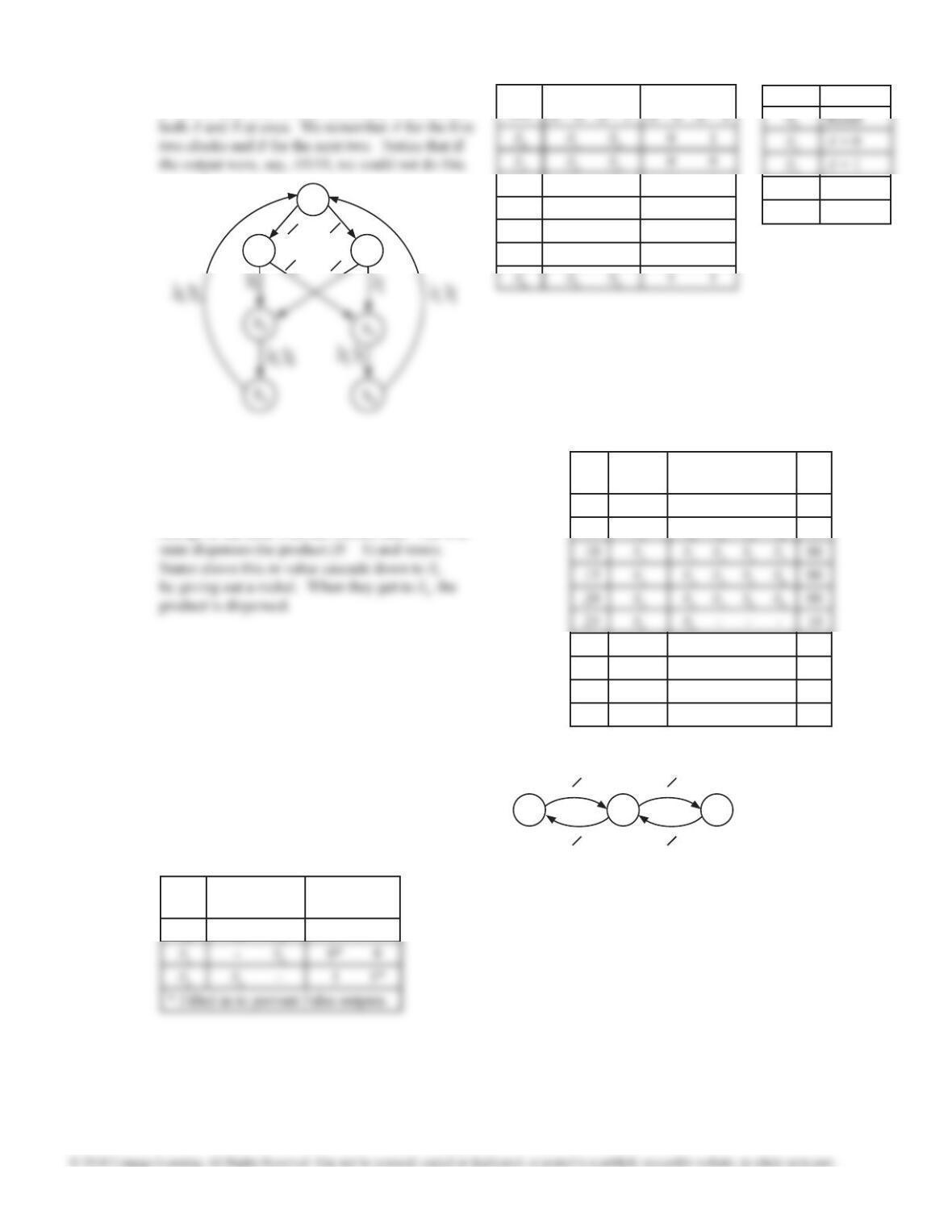
State
X = 0
X = 1
X =0
X = 1
Distinguishing between legal and illegal sequences
and combining sequences with the same parity
produces the table below.
This table can be reduced using techniques of Unit
15. Alternatively, it can be reduced by noting that
all sequences of length 2 and all of length 3 only
need to be distinguished by their parity.
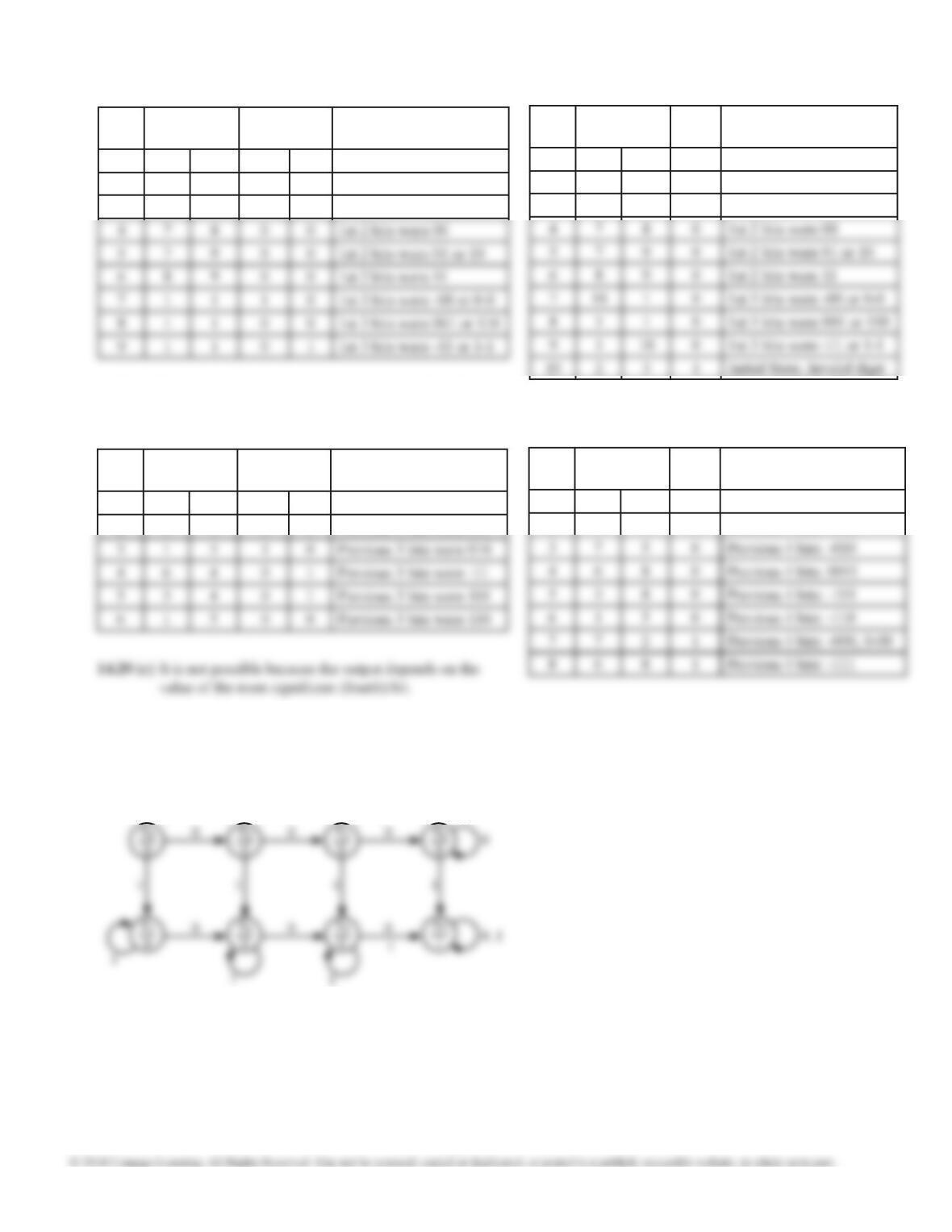
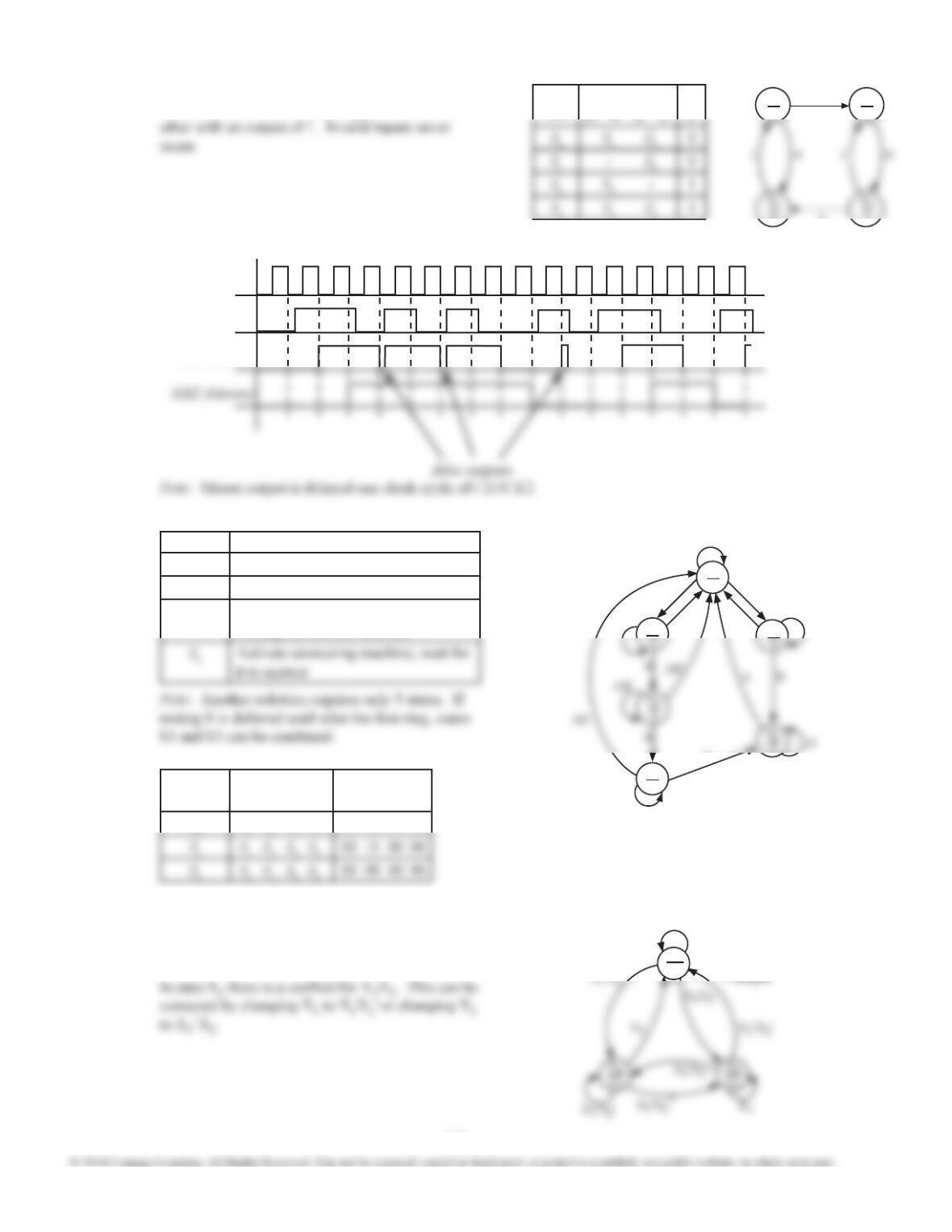
State
X = 0
X = 1
X =0
X = 1
Distinguishing between legal and illegal sequences
and combining sequences with the same parity
produces the table below.
This table can be reduced using techniques of Unit
15. Alternatively, it can be reduced by noting that
all sequences of length 2 and all of length 3 only
need to be distinguished by their parity.