Unit 13 Solutions
Unit 13 Problem Solutions
Notice that this is a shift register. At each falling clock edge, Q3 takes on the value Q2
had right before the clock edge,
Q2
takes on the value Q1 had right before the clock edge, and Q1 takes on the value X had right before the clock edge.
13.2
A+ = AKA
‘ + A’JA= A (B’ + X) + A’(BX’ + B’X)
B+ = B’JB + BKB
‘ = AB’X + B (A’ + X’)
Z = AB
Present
State
Next State
A+B+
Z
AB X = 0 X = 1
00 00 10 0
01 11 01 0
13.3 (a)
X
A B 0 1
A+
X
A B 0 1
B+
X = 0 1 1 0 0
13.3 (b) See FLD p. 758 for solution.
13.3 (c)
13.4 (a)
X Q1
Q2 Q300 01 11 10
00
01
0
0
0
0
0
0
0
0
X Q1
Q2 Q300 01 11 10
00
01
0
1
0
1
0
1
0
1
X Q1
Q2 Q300 01 11 10
00
01
1
1
1
1
1
1
1
1
X Q1
Q2 Q300 01 11 10
00
01
0
0
0
0
1
1
1
1
13.4 (b – d) See FLD p. 759 for solutions.
Unit 13 Solutions
146
13.6 (a)
Mealy machine, because the output, Z, depends on
the input X as well as the present state.
13.5 (a) 13.5 (b) Z
X A
B C 00 01 11 10
00
01
1
1
1
1
0
0
0
0
13.5 (c – d) See FLD p. 759 for solutions.
After a rising clock edge, it takes 4 ns for the ip-op outputs to change. Then the ROM will take 8 ns to respond to
13.6 (b) The correct output sequence is 0101. See FLD p. 760 for the timing diagram.
13.6 (c) Read the state transition table from ROM truth table. See FLD p. 760 for the state graph and table.
Present
State
Next State
Q1
+Q2
+Z
Q1Q2X = 0 X = 1 X = 0 X = 1
00 10 10 0 0
13.7 (a) Q1+ = J1Q1‘ + K1‘Q1 = XQ1‘ + XQ2‘Q1
Q2+ = J2Q2‘ + K2‘Q2 = XQ2‘ + XQ1Q2
Z = X’Q2‘ + XQ2
Z
Q2
false
{
false
{
Z = 00011
13.7 (c)
Present
State
Next State
Q1
+Q2
+Z
Q1Q2X = 0 X = 1 X = 0 X = 1
00 00 11 1 0
Unit 13 Solutions
147
13.8 (a) Q1+ = J1Q1‘ + K1‘Q1 = XQ2‘Q1‘ + X’Q1
Q2+ = J2Q2‘ + K2‘Q2 = X Q1Q2‘ + X’Q2
Z = XQ2‘ + X’Q2
11
S0
0100
S3
S1S2
1
1
01
10
10
00
1 0
1 01
13.9 (a) Q1+ = D1 = (X1‘ + X2‘ + Q1)(Q1 + Q2)(X1‘ + Q2)
Q2+ = D2 = (X1‘X2‘ + Q1‘)(X1X2 + Q2)
Z = Q1Q2‘
Clock
X
X
2
1
13.9 (b)
13.10(a) Q1+ = D1 = X1X2Q1 + Q1Q2 + X2Q2
Q2+ = D2 = (X1‘ + X2‘)Q2 + (X1 + X2)Q1‘
Z = Q1Q2‘
S0
0
S1
0
00
01, 10, 11
00, 10
01, 1100, 01, 10
Present
State
Next State
Q1
+Q2
+Z
Q1Q2X = 0 X = 1 X = 0 X = 1
00 00 10 0 1
State
Present
State
Next State
X1X2Z
Q1Q200 01 11 10
S000 00 01 01 00 0
State
Present
State
Next State
X1X2 = Z
Q1Q200 01 11 10
S000 00 01 01 01 0
Unit 13 Solutions
148
Clock
X
Q
S0
0100
S2
10
13.11 (a)
(cont.)
13.11
(b)
13.11 (a)
X
Q1 Q20 1
00
01
0
0
0
1
X
Q1 Q20 1
00
01
0
1
1
0
X
Q1 Q20 1
00
01
0
1
1
0
Notice that Z depends on the input X, so this is a
Mealy machine.
Q1
+ = J1Q1
‘ + K1
‘Q1 = XQ1
‘Q2 + X’Q1
Q2
+ = J2Q2
‘ + K2
‘Q2 = XQ1
‘Q2
‘ + X’Q2
Z = Q2 ⊕ X = XQ2
‘ + X’Q2
Clock
X
1
Z = (0)000110
13.10(b) 13.10(c)
13.12(a)
X1 X2
Q1 Q200 01 11 10
00
0
0
0
0
00 01 11 10
00
0
1
1
1
X1 X2
Q1 Q2
Notice that Z does not depend on either input, so
this is a Moore machine.
Q1
+ = X1X2Q1 + Q1Q2 + X1Q2
Unit 13 Solutions
149
13.15 (a)
X Q1
Q2 Q300 01 11 10
00
01
0
0
0
0
1
1
0
0
X Q1
Q2 Q300 01 11 10
00
01
0
1
0
1
0
1
0
1
X Q1
Q2 Q300 01 11 10
00
01
1
1
1
1
1
1
1
1
X Q1
Q2 Q300 01 11 10
00
01
0
0
0
0
1
1
1
1
13.14
Clock
X
Q
1
Clock
X
1
13.12(b)
13.13
Clock
X
Q
1
Q
State
Present
State
Next State
X1X2 = Z
Q1Q200 01 11 10
S000 00 01 01 01 0
S0
0
S1
0
00
01, 10, 11
00, 01
13.12(a)
(cont.)
Unit 13 Solutions
150
13.16 (a)
X Q1
Q2 Q300 01 11 10
00
01
1
0
1
0
0
0
0
0
X Q1
Q2 Q300 01 11 10
00
01
0
0
1
0
1
1
1
1
X Q1
Q2 Q300 01 11 10
00
01
0
0
0
0
1
1
1
1
State
Present
State
Next State
Q1
+Q2
+Q3
+Z
Q1Q2Q3X = 0 X = 1 X = 0 X = 1
S0000 100 011 1 0
S1001 000 011 0 1
X Q1
Q2 Q300 01 11 10
00
01
1
0
1
0
0
1
0
1
S2
S4
01
10
01
10
10
01
Clock
X
Q
13.15 (b) 13.15 (c)
From diagram: 0, 1, (0), 1, 0, 1
From graph: 0, 1, 1, 0, 1
(they are the same, except for the false output)
State
Present
State
Next State
Q1
+Q2
+Q3
+Z
Q1Q2Q3X = 0 X = 1 X = 0 X = 1
S0000 001 101 0 1
S1001 011 111 0 1
S3S6
S1
S0
S5
0011
10
01
10
01
10
0011
,
00
00
13.15 (a)
(cont.)
Unit 13 Solutions
151
Clock
X
13.16 (c)
From diagram: 1 0 1 (0) 1 1
From graph: 1 0 1 1 1
(they are the same, except for the false
output)
13.16 (b)
S2
001
011
0
S3
101
111
0
S4
000
000
0
S6
000
000
1
0,1
0,1
13.17 (a) Circuit 1
Present
State
Next
X = 0
State
X = 1
Output
Z
S0
001
011
0
S1
101
101
0
S
2
S
3
S
7
11
011
S3
101
111
0
100
S4
000
010
0
101
S5
000
000
0
110
S6
010
010
1
111
S7
010
010
0
00
0,1
10 0
1
Circuit 2
Q2Q1Q0
Present
State
Next
X = 0
State
X = 1
Output
Z
000
S0
001
011
0
001
S1
101
101
0
010
S2
001
011
1
Both circuits examine 3 consecutive inputs and
produce an output of 1 if the three consecutive
inputs represent a binary number larger than 5.
Circuit 1 produces the 1 output when the 3rd bit
is present on the input, i.e., prior to the active
clock edge when the 3rd bit is present. Circuit 2
produces the 1 output when the circuit enters the
.
13.17 (b) 13.17 (d)
Unit 13 Solutions
13.20 (a)
0
0, 1
Clock
Z
Q1+ = J1Q1‘ + K1‘Q1
= (XQ2‘ + XQ’2)Q1‘ + (X + Q2‘)Q1
13.20 (b)
The circuit is a Moore circuit. State 2 is
unused.
13.20 (c) Z = (0)01101
Present
State
Next State
Q1
+Q2
+Z
Q1Q2X = 0 X = 1
00 00 11 0
0
0
11
0
00 10
1
0
1
1
13.18 (a) D1 = Q1′ + Q2, D2 = x, z = Q1 + Q2′
Present
Q1Q2
Next
x = 0
State
x = 1
Output
z
00
10
11
1
13.18 (b)
13.18 (c)
13.18 (d) Any input sequence ending with an odd number of
0’s (1, 3, 5, etc.) followed by a single 1.
0, 1
11
0
1
0, 1
1
13.19 (b)
13.19 (d) Any sequence ending with an odd number of 0’s
(1, 3, 5, etc.) followed by an odd number of 1’s.
Present
Q1Q2
Next
x = 0
State
x = 1
Output
z
00
10
11
1
Unit 13 Solutions
153
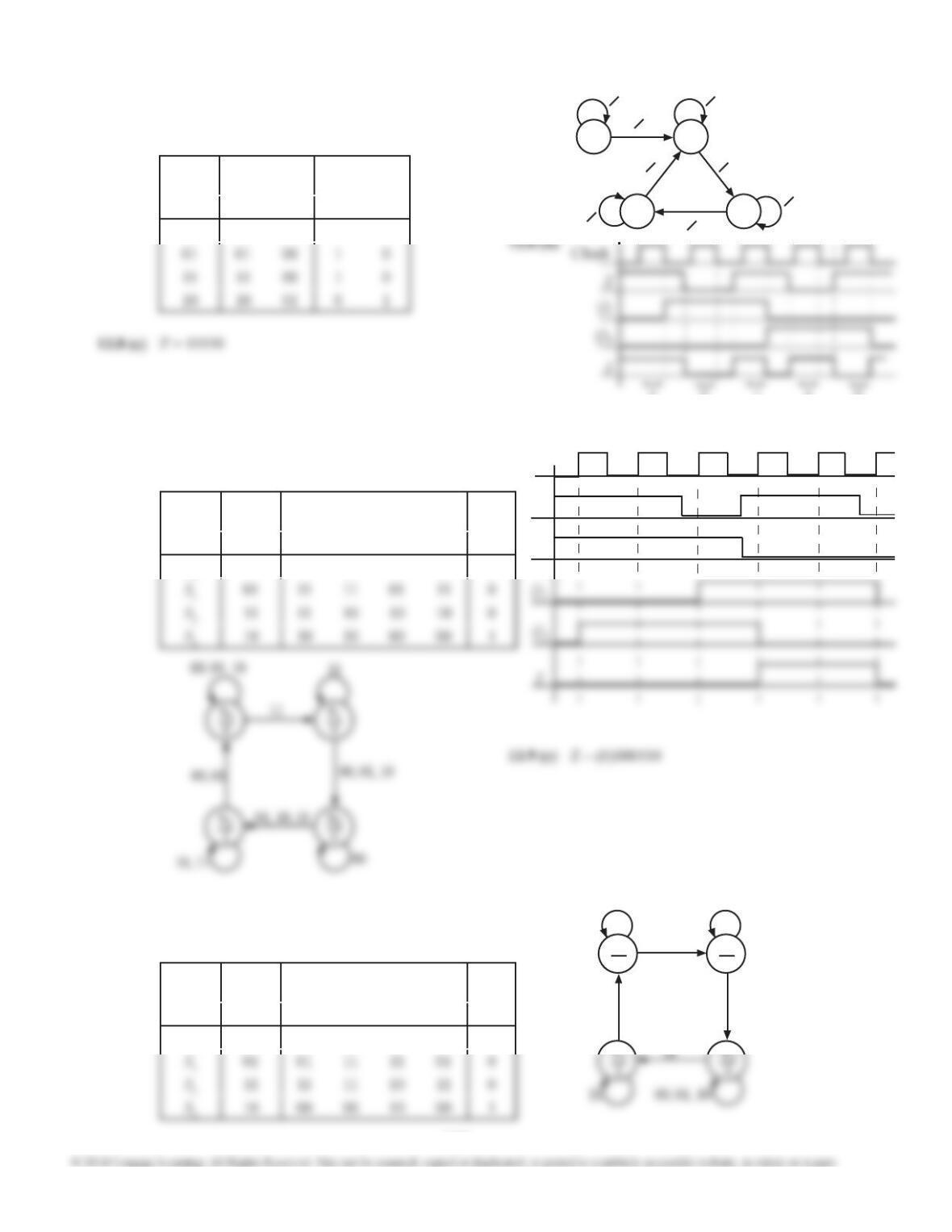
13.21 Clock Cycle Information Gathered
1Q1Q2 = 00, X = 0 ⇒ Z = 1, Q1
+Q2
+ = 01
2Q1Q2 = 01, X = 0 ⇒ Z = 0; X = 1 ⇒ Z = 1, Q1
+Q2
+ = 11
3Q1Q2 = 11, X = 1 ⇒ Z = 1; X = 0 ⇒ Z = 0, Q1
+Q2
+ = 10
0
Present
State
Next State
Q1
+Q2
+Z
Q1Q2X = 0 X = 1 X = 0 X = 1
00 01 10 1 0
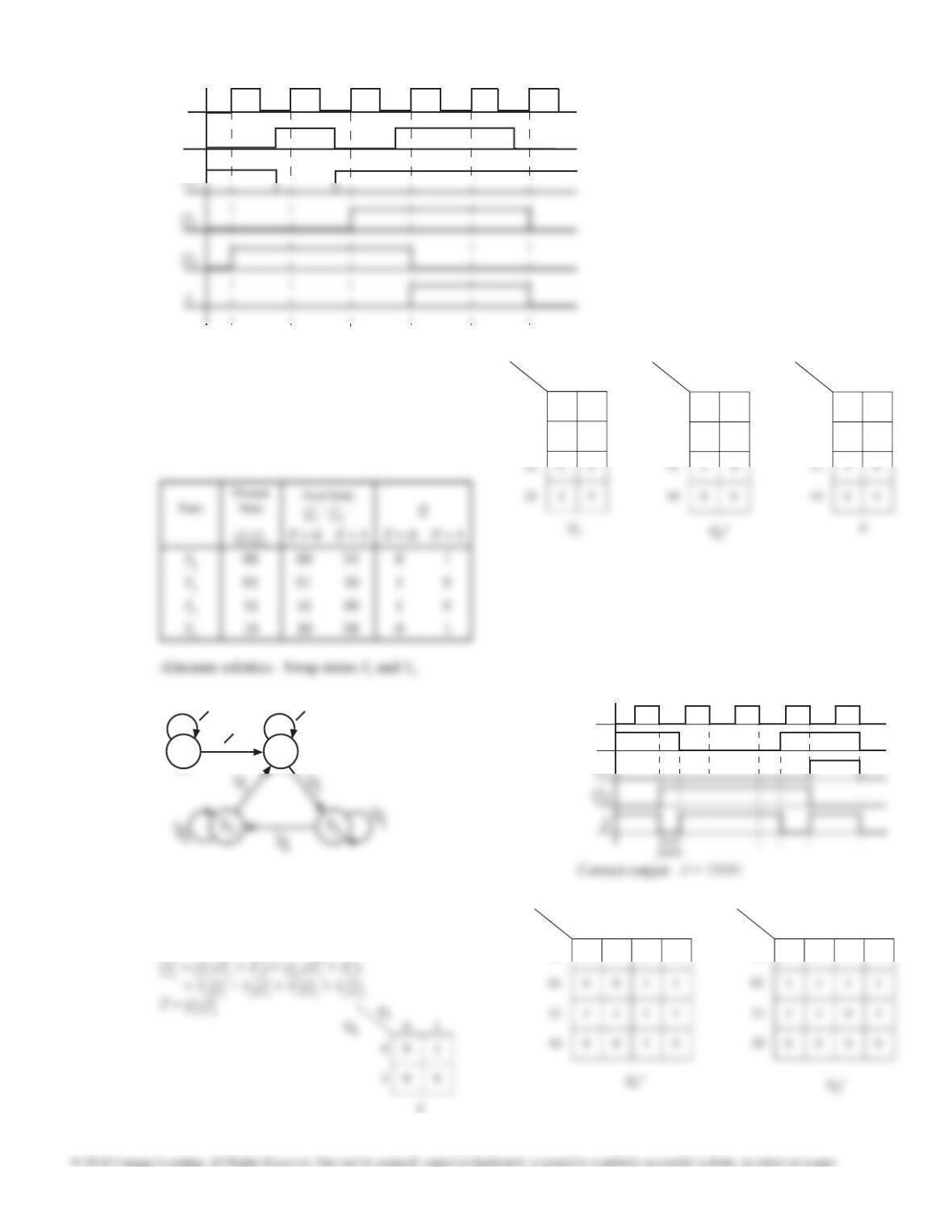
13.22 Clock Cycle Information Gathered
1Q1Q2 = 00, X = 0 ⇒ Z = 0, Q1
+Q2
+ = 10
2Q1Q2 = 10, X = 0 ⇒Z = 1; X = 1⇒ Z = 0, Q1
+Q2
+ = 01
3Q1Q2 = 01, X = 1 ⇒ Z = 0; X = 0⇒ Z = 1, Q1
+Q2
+ = 10
Present
State
Next State
Q1
+Q2
+Z
X = 0 X = 1
Q1Q2X = 0 X = 1
00 10 11 0 1
1
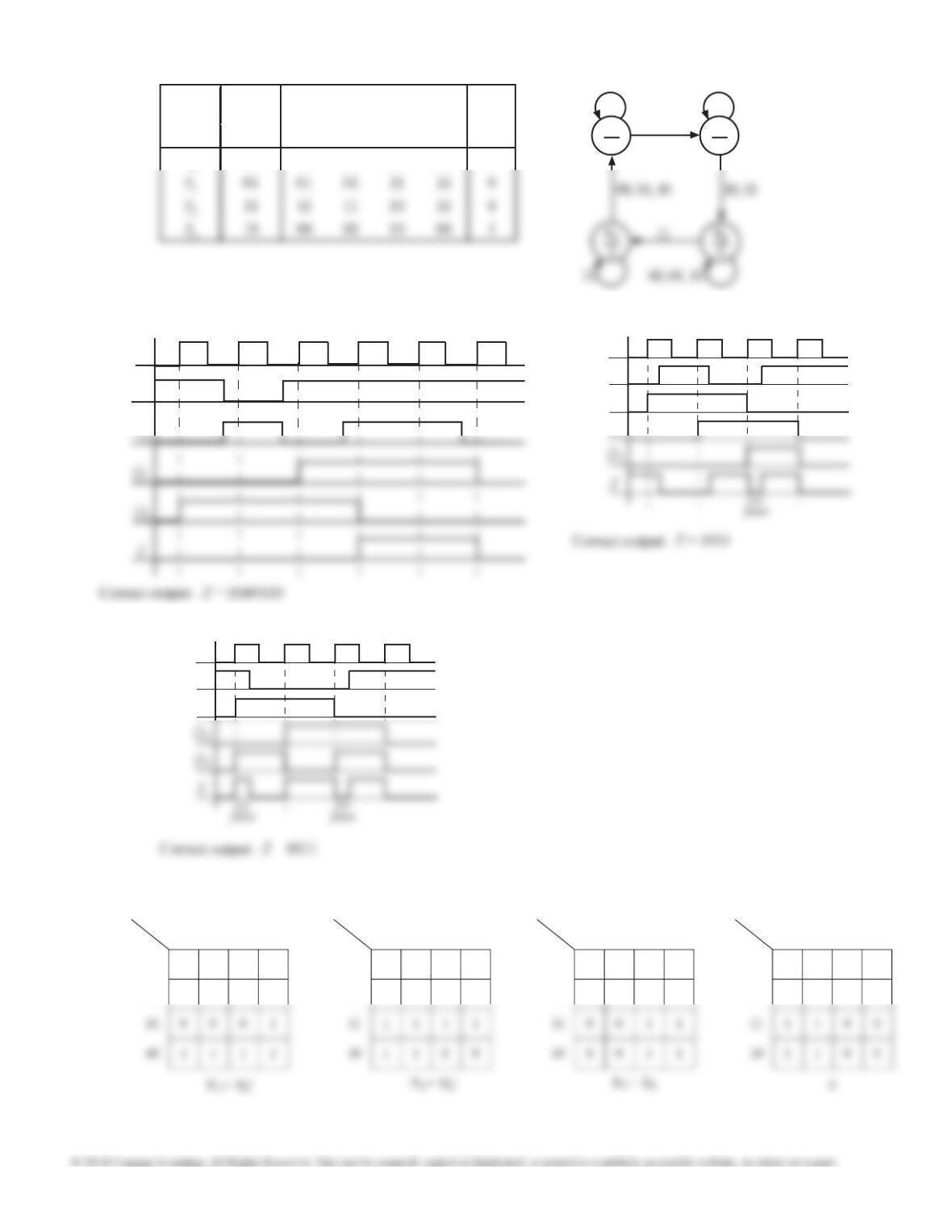
13.23 Clock Cycle Information Gathered
1Q1Q2 = 00, X1X2 = 01 ⇒ Z1Z2 = 10, Q1
+Q2
+ = 01
2Q1Q2 = 01, X1X2 = 01 ⇒ Z1Z2 = 01; X1X2 = 10 ⇒ Z1Z2 = 10, Q1
+Q2
+ = 10
Note: When Q1Q2 = 01,
the outputs Z1Z2 vary
depending on the inputs
X1X2, so this is a Mealy
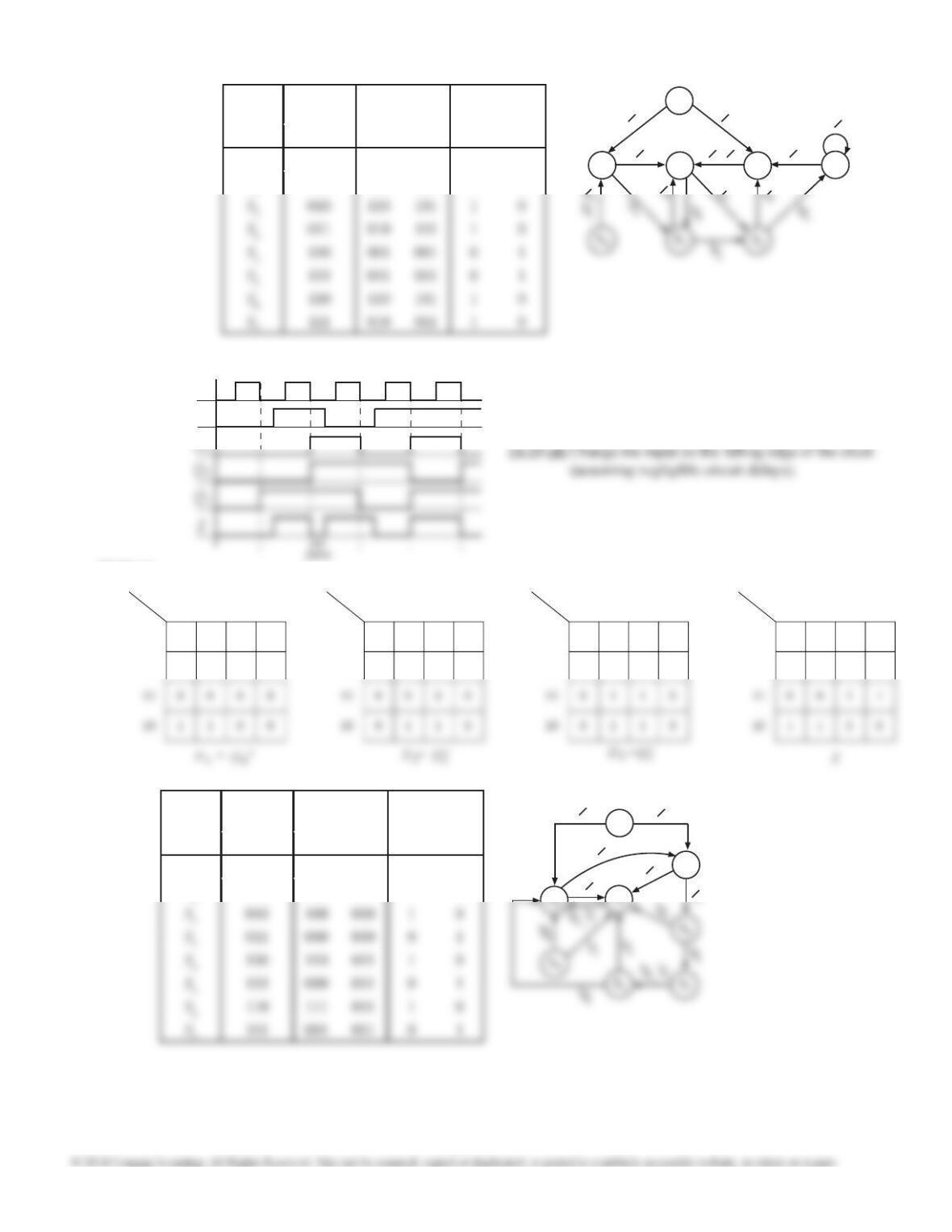
Present
State
Q1
+Q2
+
X1X2=
Z1Z2
X1X2=
Q1Q200 01 11 10 00 01 11 10
00 ? 01 ? ? ? 10 ? ?
Unit 13 Solutions
154
13.26 (b) Present
State
Q1
+Q2
+
X1X2=
Z1Z2
X1X2=
Q1Q200 01 10 11 00 01 10 11
00 00 00 01 01 10 10 10 10
01 11 11 10 10 00 10 01 11
13.26 (a)
Clock
X
X
2
1
13.25(a)
S0
0100
S3
10
Clock
X
Q
Q1+ = D1 = X’Q1 + XQ1‘Q2
Q2+ = D2 = X’Q2 + XQ1‘Q2‘
Z = X’Q2 + XQ1‘Q2‘ + XQ1Q2‘
13.25(b)
13.25(c) Z = 11101
Present
Next State
13.24
Present
State
Q1
+Q2
+
X1X2=
Z1Z2
X1X2=
Q1Q200 01 11 10 00 01 11 10
00 ? 01 ? ? ? 10 ? ?
Unit 13 Solutions
155
13.27
State
Present
State
Next State
Q1
+Q2
+Q3
+Z
Q1Q2Q3X = 0 X = 1 X = 0 X = 1
S0000 001 011 0 0
Clock
X
Q1
13.28 (a)
Clock
X
A
5ns 10ns 15ns 20ns 25ns 30ns 35ns
All ip-op inputs are stable for more than the setup
time before each falling clock edge. So the circuit is
operating properly.
Transition table using a straight binary state
assignment:
13.29
Clock
A
Correct output: Z = 1 0 1 0 1
Deriving the State Table:
JK ip-op equation:
Q+ = JQ’ + K’Q
Unit 13 Solutions
156
A+
X A
B C 00 01 11 10
00
01
0
1
1
1
1
0
0
0
B+
X A
B C 00 01 11 10
00
01
0
1
0
0
1
0
1
1
C+
X A
B C 00 01 11 10
00
01
0
1
0
1
0
1
1
1
Z
X A
B C 00 01 11 10
00
01
1
0
1
1
0
0
0
0
S0
S1
01
00
01
10
10
11
11
00
11
00
From the Karnaugh maps, we can get the state table
that follows:
State
Present
State
Next State
A+B+C+Z
ABC X = 0 X = 1 X = 0 X = 1
S0000 000 110 1 0
S1001 111 001 0 0
R = X2 (X1
‘ + B)
S = X2
‘ (X1
‘ + B’)
A+ = A[(X2) (X1
‘ + B)]‘ + X2
‘ (X1
‘ + B’)
= A (X2
‘ + X1B’) + X2
‘X1
‘ + X2
‘B’
A+ = AX2
‘ + AX1B’ + X2
‘X1
‘ + X2
‘B’
13.30
State
Present
State
A+B+
X1X2=
Z1Z2
X1X2=
AB 00 01 10 11 00 01 10 11
S000 11 01 10 00 10 10 00 00
13.30
(cont.)
13.29
(cont.)