125
Unit 12 Solutions
Unit 12 Problem Solutions
12.1 Consider 3 × Y = Y + Y + Y, that is, we need to add Y to itself 3 times. First, clear the accumulator before the first
rising clock edge so that the X-register is 000000. Let the Ad pulse be 1 for 3 rising clock edges and let the Y register
12.2 Serial input connected to D0 for left shift.
Sh = 0, L = 1 causes a left shift.
Sh = 1, L = 1 or 0 causes a right shift
12.3
Serial Out
Q3Q2Q1Q0
See FLD Appendix E for solution.
Present
State
D C B A
Next State
D+C+B+A+
Flip-Flop
Inputs
TDTCTBTA
0 0 0 0 0 0 0 1 0 0 0 1
0 0 0 1 0 0 1 0 0 0 1 1
0 0 1 0 0 0 1 1 0 0 0 1
0 0 1 1 0 1 0 0 0 1 1 1
12.4 (a)
T
D
D
D‘
T
C
C
C‘
T
B
B
B‘
T
A
A
A‘
1
126
Unit 12 Solutions
12.4 (b) 12.5 Equations for C, B, and A are from Equations (12-
12.6 In the following state graph, the first ip-op (C)
takes on the required sequence 0, 0, 1, 0, 1, 1,
(repeat).
000
A
C
B A 0 1
00
01
1
0
0
0
+C
C
B A 0 1
00
01
0
1
0
1
+
B
C
B A 0 1
00
01
0
0
1
1
+
C
C
B A 0 1
00
X
0
+B
C
B A 0 1
00
X
0
+A
C
B A 0 1
00
X
1
+
12.7 (a) C B A C+ B+ A+
0 0 0 X X X
0 0 1 0 1 1
0 1 0 1 1 0
C
B A 0 1
00
01
X
0
1
0
TC
C
B A 0 1
00
01
X
1
0
0
T
B
C
B A 0 1
00
01
X
0
1
1
TA
12.7 (b)
C B A C+.B+ A+
0 0 0 0 0 1
The binary counter using D ip-ops is obtained
127
Unit 12 Solutions
12.8 (a) C B A C+ B+ A+
0 0 0 X X X
0 0 1 0 1 1
0 1 0 1 1 0
C+
C
B A 0 1
00
X
0
B+
C
B A 0 1
00
X
0
A+
C
B A 0 1
00
X
1
C
B A 0 1
00
01
X
X
1
X
JA
C
B A 0 1
00
01
X
1
0
0
JB
C
B A 0 1
00
01
X
0
X
X
JC
12.8 (b)
C
B A 0 1
00
01
X
0
X
1
KA
C
B A 0 1
00
01
X
X
X
X
KB
C
B A 0 1
00
01
X
X
1
0
KC
C
B A 0 1
00
01
X
0
0
1
RA
C
B A 0 1
00
01
X
0
X
X
RB
C
B A 0 1
00
01
X
X
1
0
RC
C
B A 0 1
00
01
X
X
1
0
SA
S
C
B A 0 1
00
01
X
1
0
0
B
C
B A 0 1
00
01
X
0
0
X
S = C’A’
C
SC
In state 000,
SC = BA’ = 0, RC = B’A’ = 1, C+ = 0
128
Unit 12 Solutions
12.9 (a) Q Q+ M N
0 0 0 0 0X
0 1
}
C B A C+ B+ A+
0 0 0 0 0 1
A+
C
B A 0 1
00
01
1
1
0
0
B+
C
B A 0 1
00
01
0
1
0
0
C+
C
B A 0 1
00
01
0
0
0
1
MA
C
B A 01
00
01
1
X
0
X
MB
C
B A 0 1
00
01
0
1
0
0
MB = C’A
MC
C
B A 0 1
00
01
0
0
X
X
NA
C
B A 0 1
00
01
X
1
X
0
NB
C
B A 0 1
00
01
X
X
X
X
NB = C’
NC
C
B A 0 1
00
01
X
X
0
1
12.10
12.9 (b)
See Lab Solutions for Unit 12 in this manual.
129
Unit 12 Solutions
12.12 (a) When ShLd = 00, the MUX for ip-op i selects Qi to hold its state
When ShLd = 01, the MUX for ip-op i selects Di to load.
When ShLd = 10 or 11, the MUX for ip-op i selects Qi-1 to shift left.
SI
D
Q
D
Q Q D D
Q
3 2 1 0
12.12 (b) Q3
+ = Ld’Sh’Q3 + LdSh’D3 + ShQ2; Q2
+ = Ld’Sh’Q2 + LdSh’D2 + ShQ1; Q1
+ = Ld’Sh’Q1 + LdSh’D1 + ShQ0
Q0
+ = Ld’Sh’Q0 + LdSh’D0 + ShSI
12.13 Notice that Sh overrides Ld when Sh = Ld = 1
Clock
Sh
12.14 (a)
E
E
‘
E
E‘
Similar to problem 12.4 (a),
TE = ABCD. TD, TC, TB and TA
12.14 (b) Similar to problem 12.4 (b),
DE = E ⊕ DBCA.
12.11 The ip-ops change state only when Ld or Sh = 1. So CE = Sh + Ld. Now only a 2-to-1 MUX is required to select
the input to the D ip-op.
D Q
D Q
D Q
D Q
SI
3 2 1 0
1
0
1
0
1
0
1
0
130
Unit 12 Solutions
12.15
J
4
Q
4
J
3
Q
3
J
2
Q
2
J
1
Q
1
4-bit Johnson counter using J-K ip-ops:
12.16 When U = 1, D = 0, add 001. When U = 0, D = 1, subtract 1: add 111.
When U = 0, D = 0, no change: add 000.
U = 1, D = 1, can never occur.
A B C D A+ B+ C+ D+
0 0 0 0 0 0 0 1
0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 1
0 0 1 1 0 1 0 0
0 1 0 0 0 1 0 1
0 1 0 1 0 1 1 0
12.17 (a) DA
A B
C D 00 01 11 10
00
01
11
10
1
1
X
X
X
X
X
X
DB
A B
C D 00 01 11 10
00
01
11
10
1
1
1
1 X
X
X
X
X
X
Q2Q0
Q1
131
Unit 12 Solutions
12.17 (b) See Table 12-7 (c) on FLD p. 398.
A B
C D 00 01 11 10
00
01
0
0
0
0
X
X
X
X
A B
C D 00 01 11 10
00
01
0
0
X
X
0
0
X
X
A B
C D 00 01 11 10
00
01
0
1
0
1
0
0
X
X
A B
C D 00 01 11 10
00
01
1
X
1
X
1
X
X
X
A B
C D 00 01 11 10
00
01
X
X
X
X
0
1
X
X
A B
C D 00 01 11 10
00
01
X
X
0
0
X
X
X
X
A B
C D 00 01 11 10
00
01
X
X
X
X
X
X
X
X
A B
C D 00 01 11 10
00
01
X
1
X
1
X
1
X
X
12.17 (c) See Table 12-5 (c) on FLD p. 395.
RA
A B
C D 00 01 11 10
00
01
X
X
X
X
1
X
X
RB
A B
C D 00 01 11 10
00
01
X
X
X
X
X
X
SA
A B
C D 00 01 11 10
00
01
X
X
X
SB
A B
C D 00 01 11 10
00
01
X
X
X
X
SC
A B
C D 00 01 11 10
00
01
1
1
X
X
SD
A B
C D 00 01 11 10
00
01
1
1
1
X
X
RC
A B
C D 00 01 11 10
00
01
X
X
X
X
X
X
RD
A B
C D 00 01 11 10
00
01
1
1
1
X
X
132
Unit 12 Solutions
12.17 (d)
TA
A B
C D 00 01 11 10
00
01
1
X
X
TB
A B
C D 00 01 11 10
00
01
X
X
TC
A B
C D 00 01 11 10
00
01
1
1
X
X
TD
A B
C D 00 01 11 10
00
01
1
1
1
1
1
1
X
X
1110 1111
Use equations to find next states for unused states.
State 1101:
JA = BCD = 0, KA = D = 1, A+ = 0
JB = CD = 0, KB = CD = 0, B+ = B = 1
12.17 (e)
See Table 12-4 on FLD p. 391.
12.18 A B C D A+ B+ C+ D+
0 0 0 0 1 0 0 1
0 0 0 1 0 0 0 0
0 1 1 0 0 1 0 1
0 1 1 1 0 1 1 0
1 0 0 0 0 1 1 1
1 0 0 1 1 0 0 0
10010001 0000
1000
0010
DA = A’B’C’D’ + AD;
DB= BD + BC + AD’;
DC = CD + BC’D’ + AD’;
12.18 (a) 12.18 (b)
12.18 (e)
JA = B’C’D’, KA = D’;
JB = AD’, KB = C’D’;
JC = BD’ + AD’, KC = D’;
133
Unit 12 Solutions
12.19 (a) Since J0 = K0 = 1, Q0 toggles when Clk
changes 1 to 0.
Q1 clears if Q3 = 1 and toggles if Q3 = 0 when
Q0 changes 1 to 0.
0000
0001
1000
0100
0101
12.19 (b)
0000
1000
1001 0011
0111
0011
0111
0101
0010
12.19 (b)
cont.
Clk
Q
J
0
Q
Clk
Q
J
1
Q
Clk
Q
J
2
Q
Clk
Q
J
3
Q
Clk
1
0 1
00
01
0-
-1
Q2Q1
1-
—
K1 = 1
Q3
0 1
00
01
—
—
Q2Q0
—
—
Q3
0 1
00
01
1-
0-
Q2Q1
-1
—
K3 = 1
Q3
134
Unit 12 Solutions
A B C A+ B+ C+
0 0 0 X X X
0 0 1 1 0 0
1 1 1 1 1 0
12.20 DA = B’ + AC; DB = AC + BC’; DC = A’B + AB’
JA = B’, KA = BC’; JB = AC, KB = A’C; JC = A’ + B’, KC = A’B’ + AB
12.20 (a)
12.20 (b)
ABCD DADBDCDD
0000 0 0 0 1
0101 x x x x
0110 x x x x
0111 x x x x
1000 x x x x
1001 x x x x
12.21(a) DA = AB’ + A D’ + BC’ or
= AB’ + B D’ + BC’ or
ABCD JAKA, JBKB, JCKC, JDKD
0000 0x, 0x, 0x, 1x
0101 xx, xx, xx, xx
0110 xx, xx, xx, xx
0111 xx, xx, xx, xx
1000 xx, xx, xx, xx
1001 xx, xx, xx, xx
12.21(b) JA = B
KA = BCD
Unit 12 Solutions
ABCD TA TB TC TD
0000 0 0 0 1
0001 0 0 1 1
0110 x x x x
0111 x x x x
1000 x x x x
1001 x x x x
12.21(c) TA = A’B + BCD
TB = CD + A’B
TC = D + A’B
TD = 1
ABCD SARA, SBRB, SCRC, SDRD
0000 0x, 0x, 0x, 10
0001 0x, 0x, 10, 01
0110 xx, xx, xx, xx
0111 xx, xx, xx, xx
1000 xx, xx, xx, xx
1001 xx, xx, xx, xx
12.21(d) SA = A’B or
= BC’ or
= BD’
RA = BCD
RC = CD
SD = D’
RD = D
12.22(a) DA = (B’+ C’+ D’)(A + B)
DB = (B’+ C’+ D’)(A + D)(A + C) or
12.22(b) JA = (B)
KA = (B)(C)(D )
12.22(c) TA = (B)(A’+ D)(A’+ C) or
= (B)(A’+ C)(C’+ D) or
= (B)(A’+ D)(C + D’)
12.22(d) SA = (B)(D’) or
= (B)(C’) or
= (B)(A’)
136
Unit 12 Solutions
ABCD DADBDCDD
0111 1 0 0 0
1000 1 0 0 1
1001 1 0 1 0
1010 1 0 1 1
12.23(a) DA = BCD + AB’
DB = B’CD + A’D’ + A’C’
ABCD JAKA, JBKB, JCKC, JDKD
0111 1x, x1, x1, x1
1000 x0, 0x, 0x, 1x
1001 x0, 0x, 1x, x1
1010 x0, 0x, x0, 1x
12.23(b) JA = BCD
KA = B
ABCD TA TB TC TD
0000 x x x x
0110 0 0 0 1
0111 1 1 1 1
1000 0 0 0 1
1001 0 0 1 1
12.23(c) TA = AB + B C D
TB = CD + AB
TC = D + AB
ABCD SARA, SBRB, SCRC, SDRD
0000 xx, xx, xx, xx
0110 0x, x0, x0, 10
0111 10, 01, 01, 01
1000 x0, 0x, 0x, 10
1001 x0, 0x, 10, 01
12.23(d) SA = BCD
RA = BC’ or
= BD’ or
RC = CD
SD = D’
RD = D
137
Unit 12 Solutions
12.24(c) TA = (B)(C’+ D)(A + C) or
= (B)(A + D )(A + C) or
12.24(d) SA = (B)(C)(D) SC = (A + D)(C’)(B + D)
RA = (B)(A) or RC = (C)(D)
12.25 (a) The counter must clear on the next clock edge
when the count is 1011 so ClrN = (Q3Q1Q0)‘.
Q3Q2Q1Q0 ClrN Ld
0000 1 0
0101 x x
0110 x x
1101 1 0
1110 1 0
12.26
12.24(a) DA = (A + B)(B’+ D)(A + C) or
= (A + B)(B’+ C)(A + D) or
= (A + B)(B’+ D)(B’+ C)
12.24(b) JA = (B)(C)(D)
KA = (B)
JB = (C)(D)
138
Unit 12 Solutions
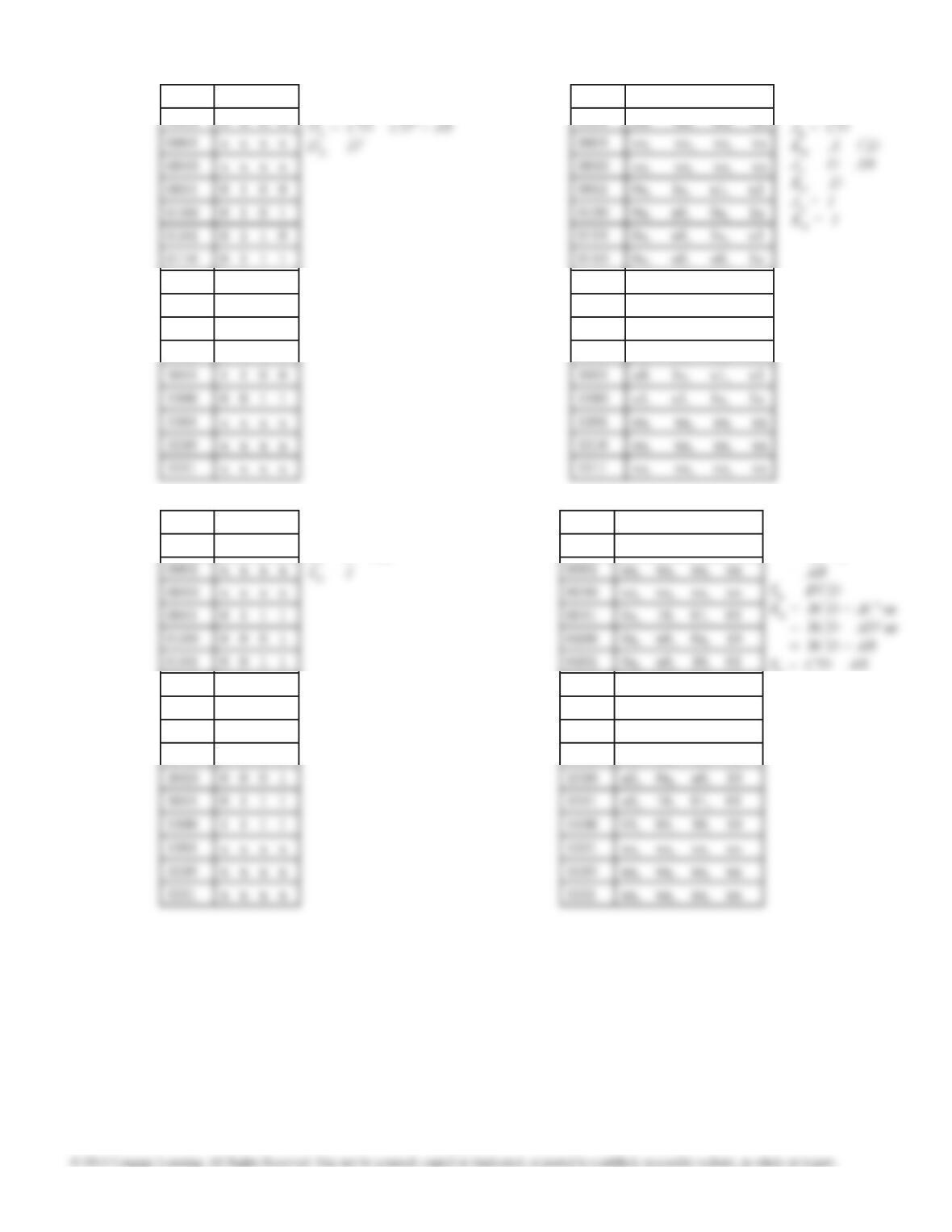
011
100
001
000
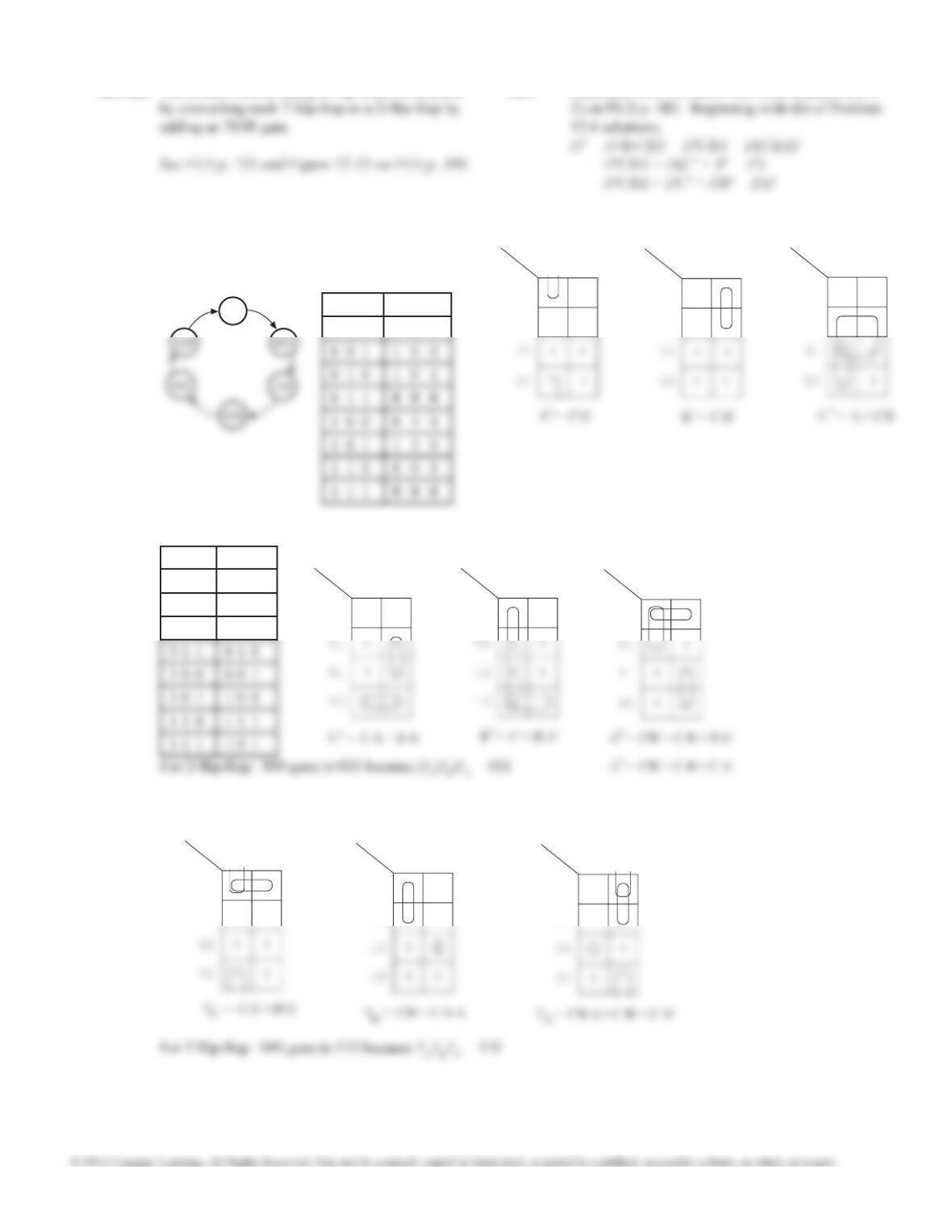
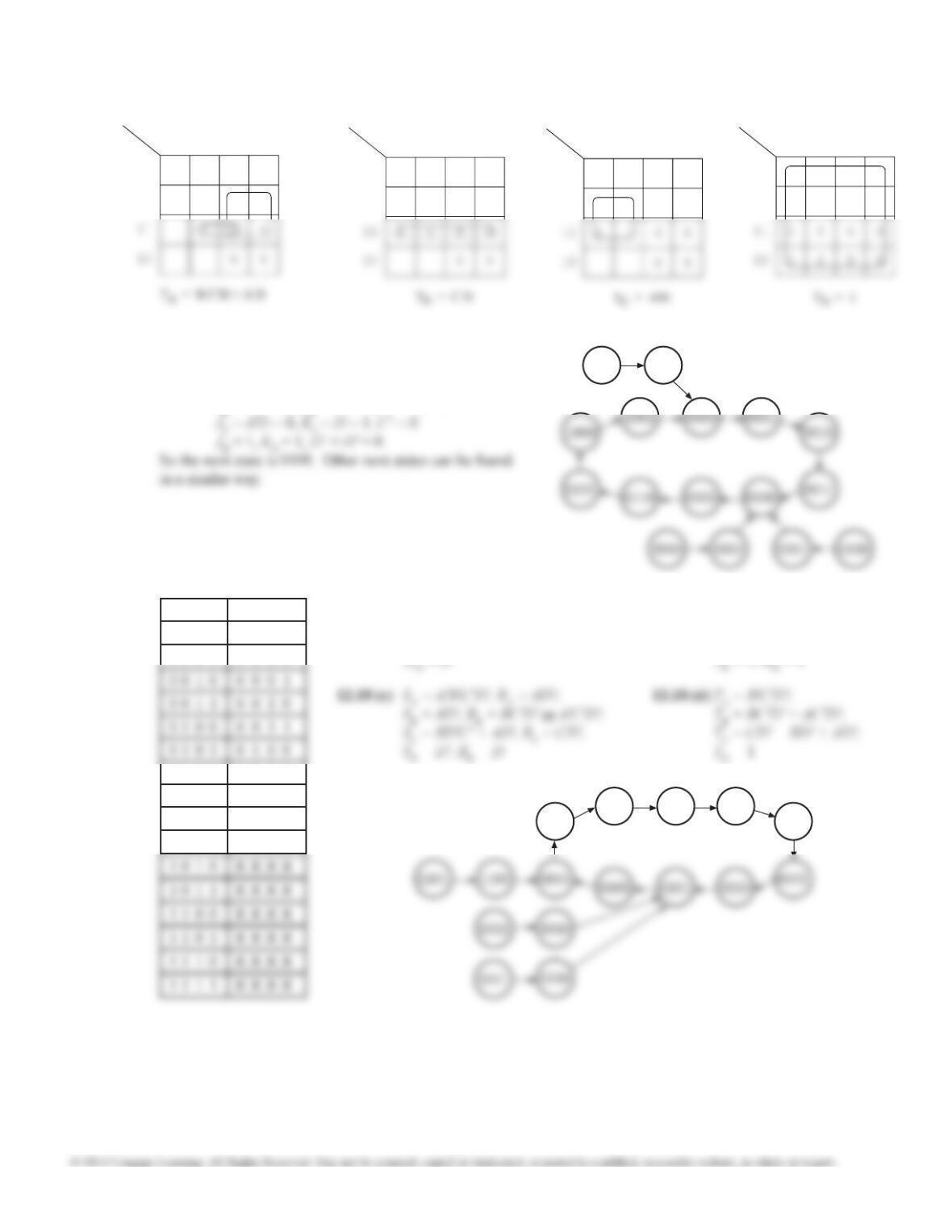
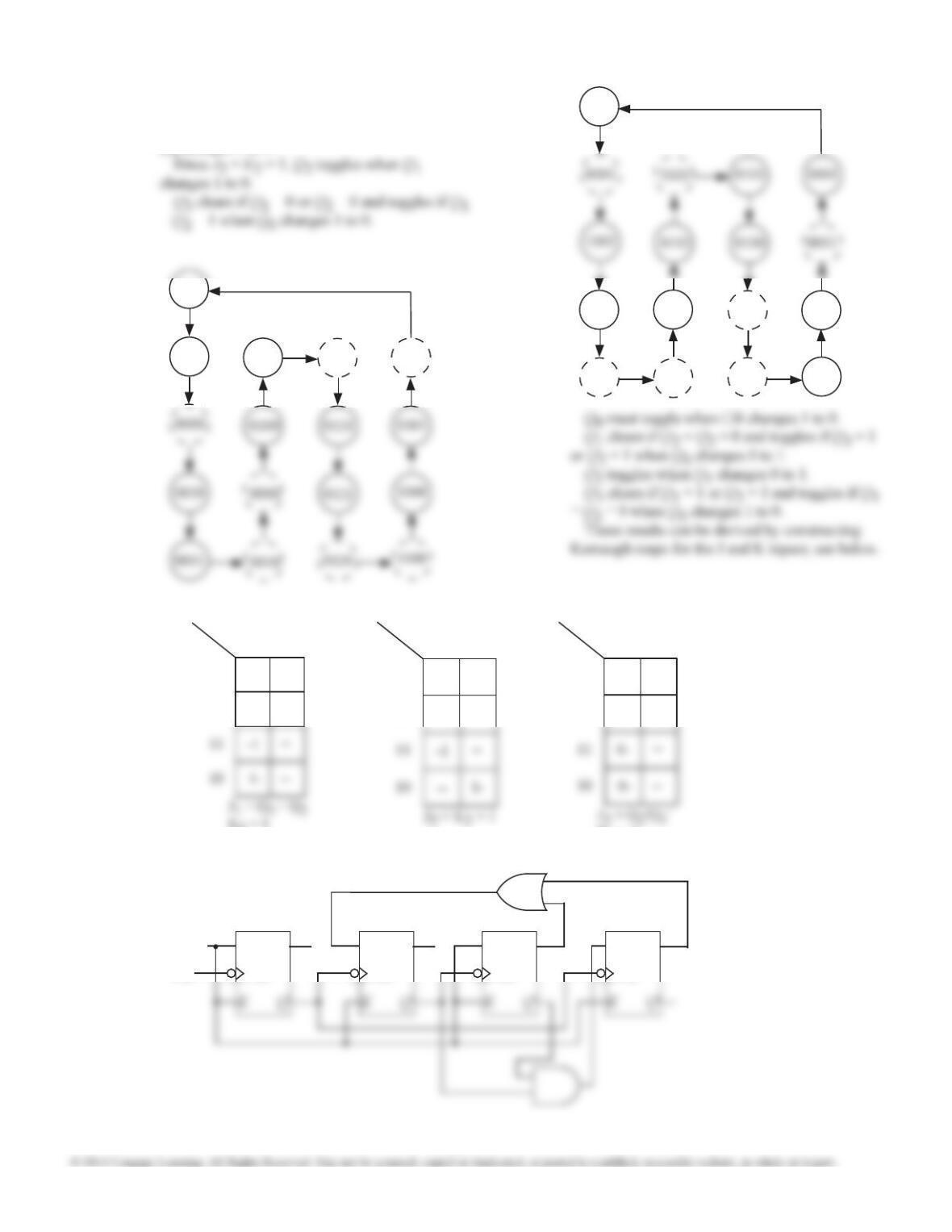
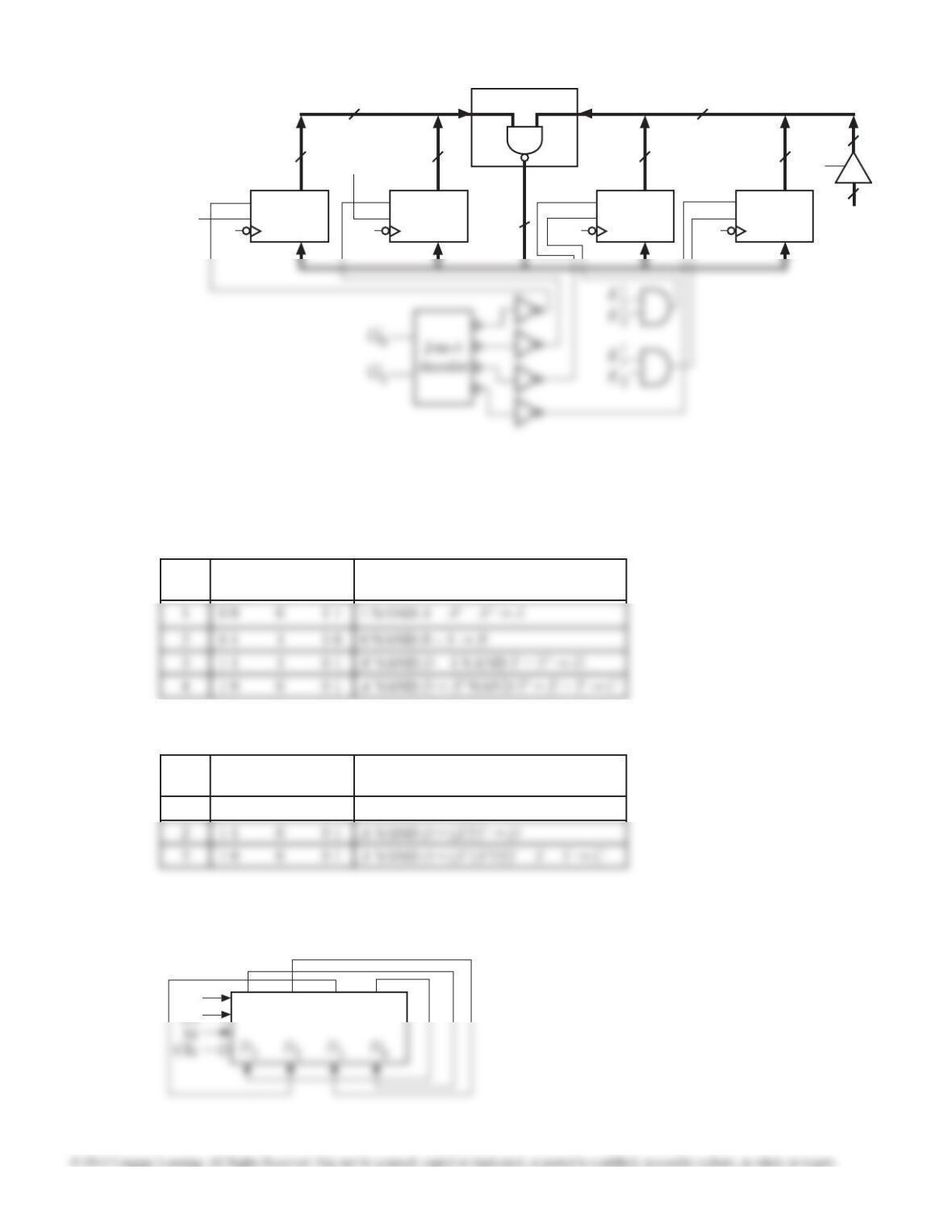
12.27 (a) (b) There are two answers:
Sin = Q2 ⊕ Q3 or
Sin = Q0 ⊕ Q3.
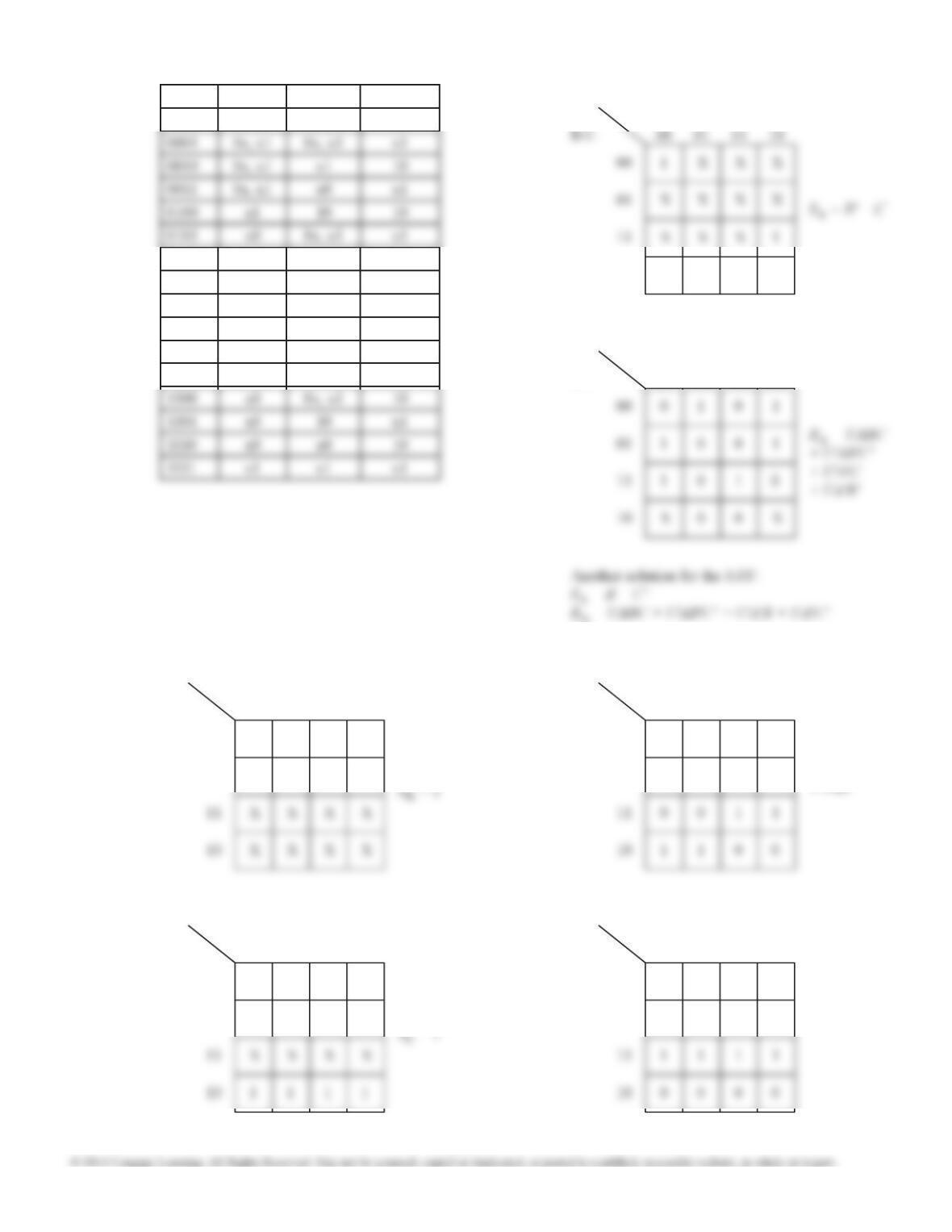
(c) The state 0000 can
Sin Q0Q1
Q2Q300 01 11 10
00
01
1
1
1
1
0
0 00
12.27 (c)
(cont.)
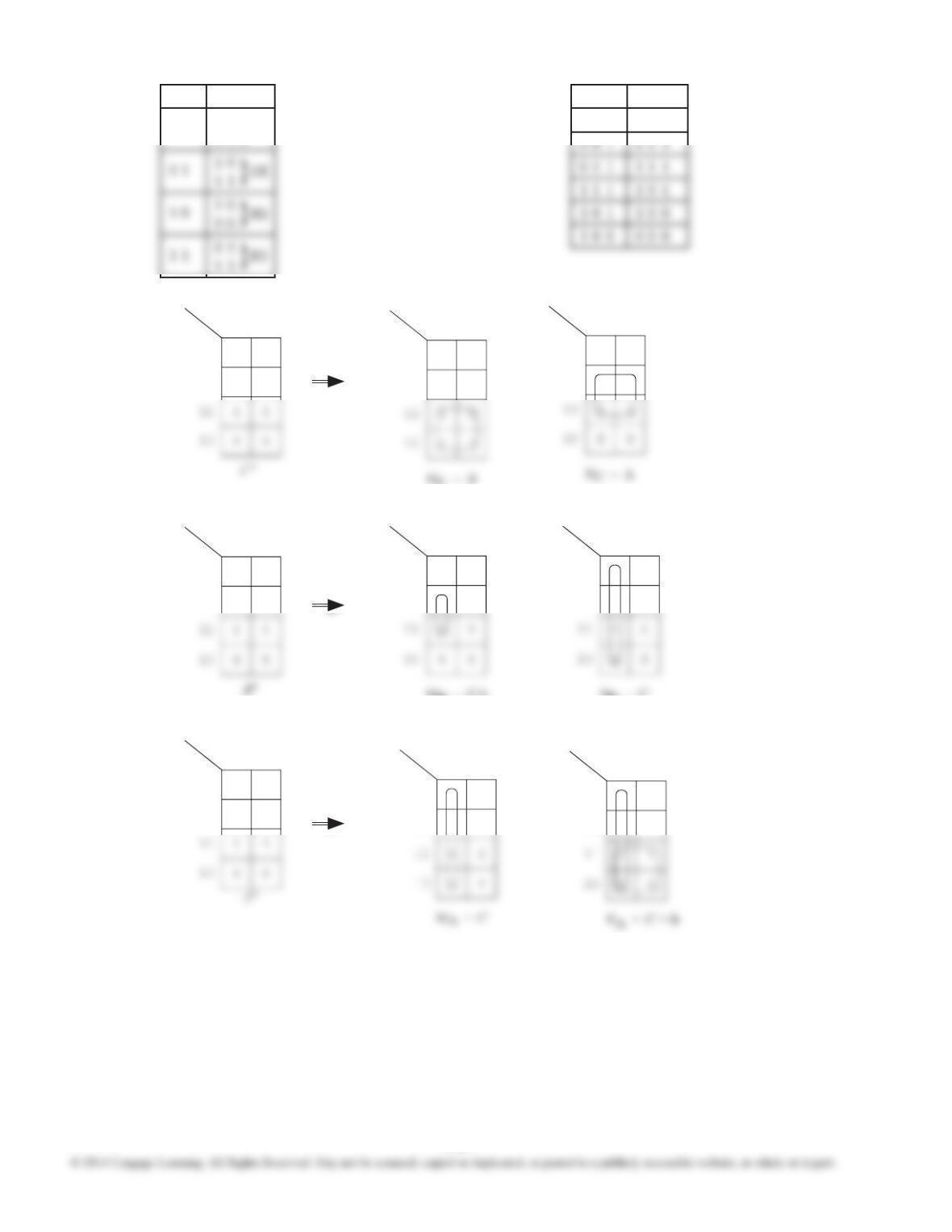
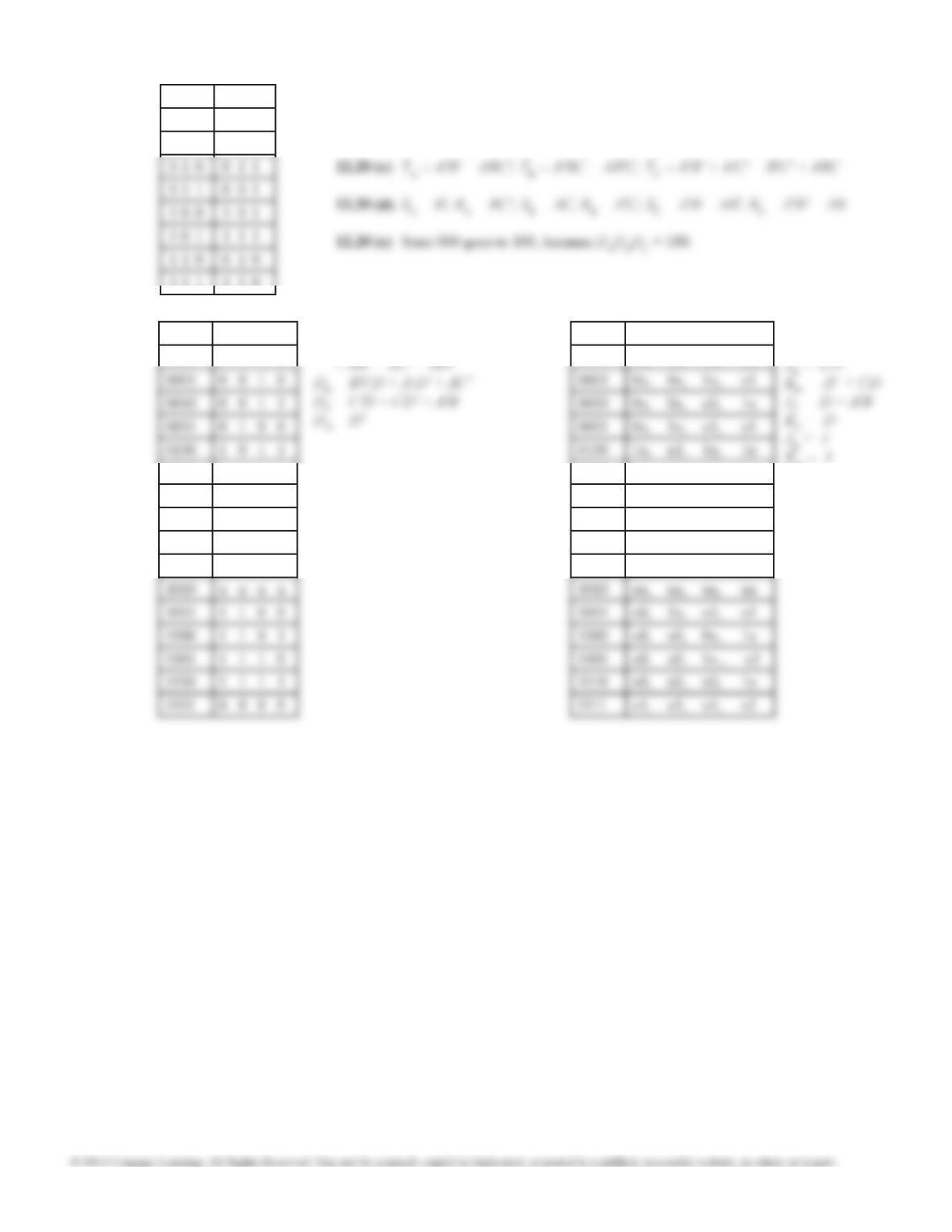
12.28 (a) 000, 100, 110, 111, 011, 001
010, 101.
12.29 (a) Skips all 1’s: Dn = Q2′Q1′
(b)Skips all 0’s:
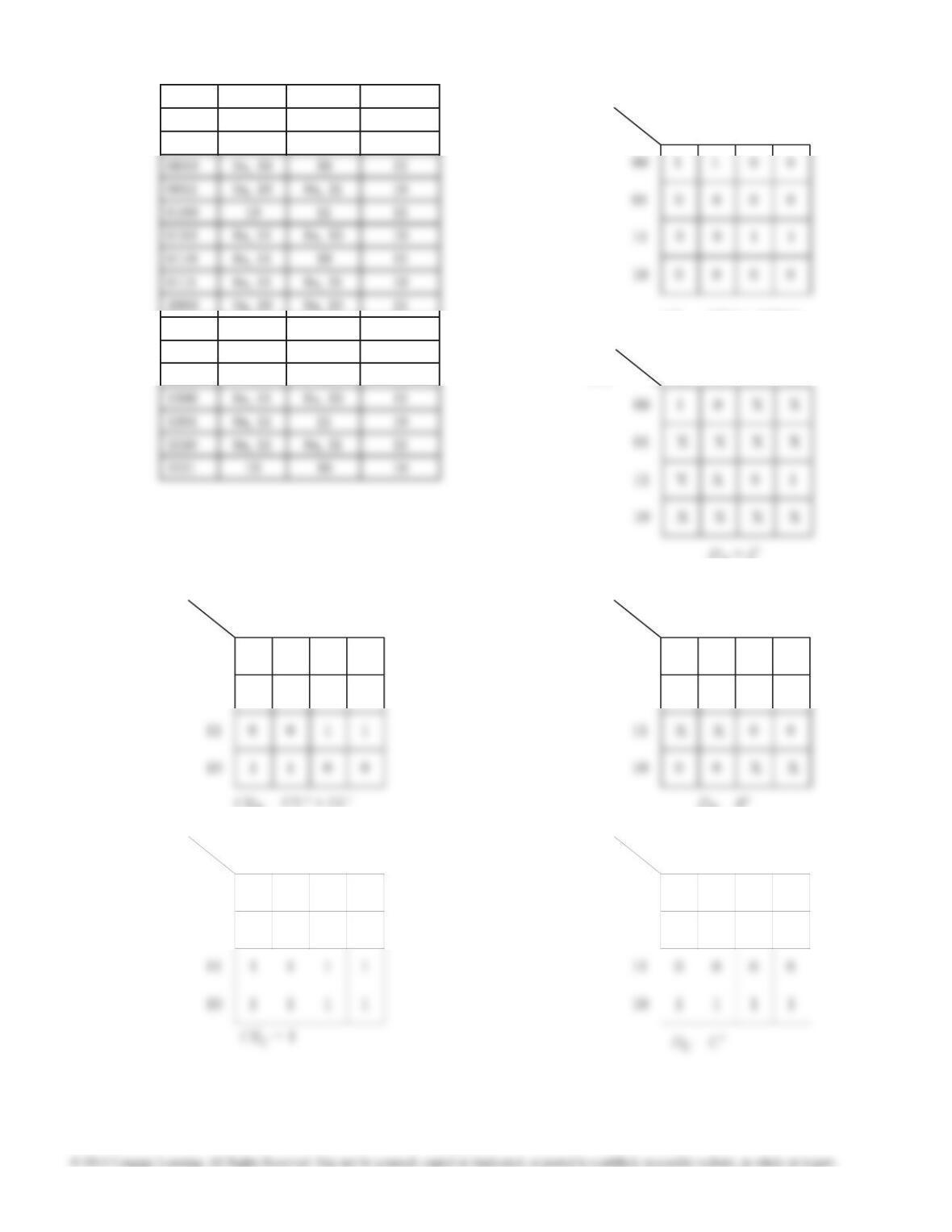
12.30 (a) The changed transition is (QnQn-1 … Q2Q1) = (11 … 10) → (01 … 11): Jn = Q1′, Kn = Q2
(b) The changed transition is (QnQn-1 … Q2Q1) = (00 … 01) → (10 … 00): Jn = Q2′, Kn = Q1
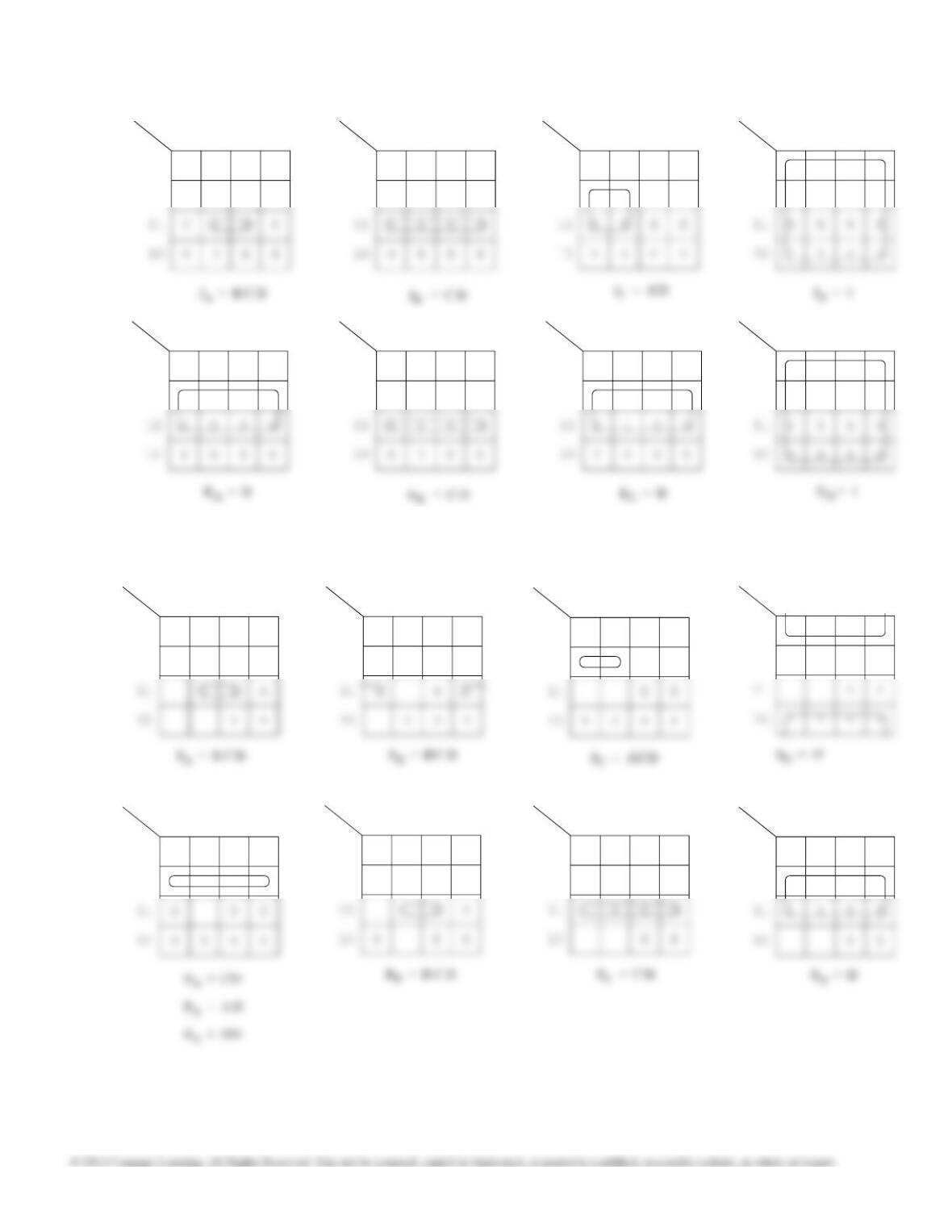
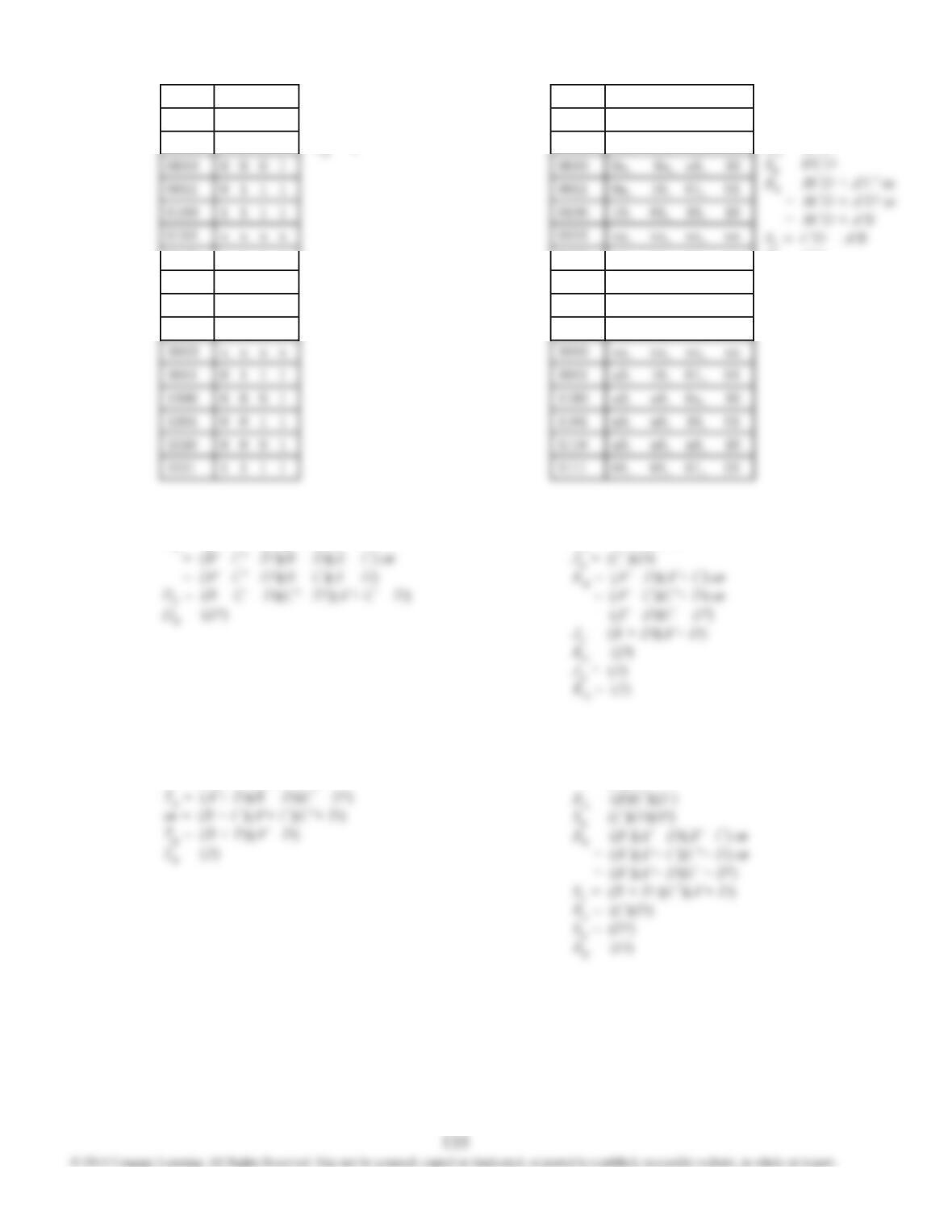
12.31 (a) All stages toggle the same as for a binary counter
except when the count becomes 1001, in which
case stages Q0, Q1 and Q2 respond the same as
for a binary counter, but Q3 must toggle (reset).
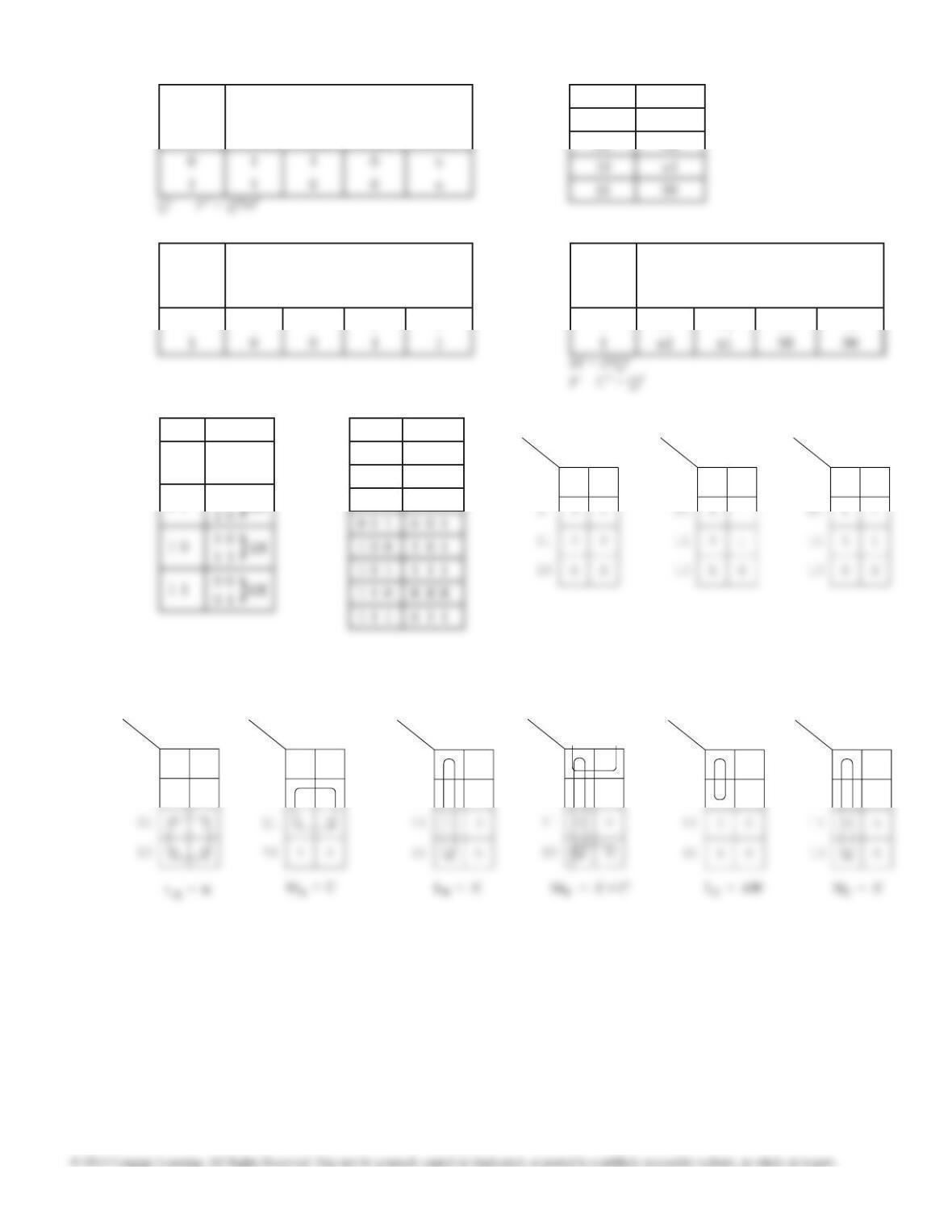
12.31 (b) All stages toggle the same as for a binary counter
for counts 0011 through 1011. For count 1100
stages 3 and 2 must reset and stage 1 must set
while stage 0 toggles as it does it does for a binary
K3 = Q0Q1Q2 + Q2Q3
K3 can be further simplified to K3 = Q2Q3.
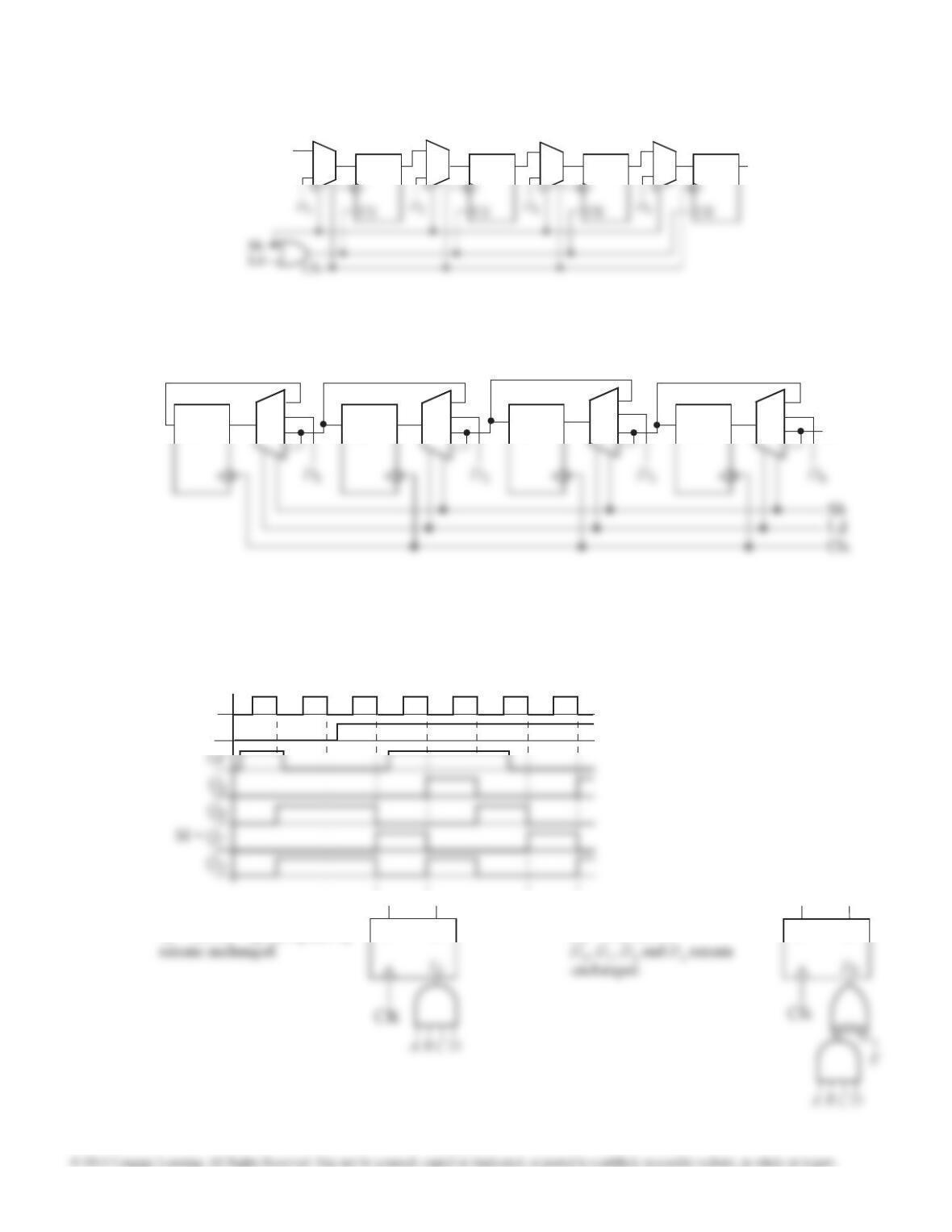
12.31 (c) To create a design that can be cascaded, we need
to add a count enable input, CE, which is ANDed
with the above equations, and terminal count
139
Unit 12 Solutions
UABC SARASBRBSCRC
0000 10 10 10
0110 x0 x1 10
0111 x0 x0 x1
1000 0x, x1 0x, x1 10
1001 0x, x1 10 x1
1010 0x, x1 x0 10
1011 10 x1 x1
12.32 (a) SA
U A
10
0
X
0
X
RA
U A
B C 00 01 11 10
SB
U A
B C 00 01 11 10
00
01
1
X
1
X
X
1
X
1
RB
U A
B C 00 01 11 10
00
01
0
1
0
1
1
0
1
0
RB = U’B’C
+ U’BC’
+ UB’C’
SC
U A
B C 00 01 11 10
00
01
1
X
1
X
1
X
1
X
RC
U A
B C 00 01 11 10
00
01
0
1
0
1
0
1
0
1
RC = C
140
Unit 12 Solutions
UABC CEADACEBDBCECDC
0000 11 11 11
0001 0x, 10 0x, 10 10
1001 0x, 10 11 10
1010 0x, 10 0x, 11 11
1011 11 10 10
12.32 (b) CEA
U A
B C 00 01 11 10
CEA = UBC + U’B’C’
U A
B C 00 01 11 10
DA = A’
DA
CEC
U A
B C 00 01 11 10
00
01
1
1
1
1
1
1
1
1
DB
U A
B C 00 01 11 10
00
01
1
X
1
X
X
1
X
1
DB = B’
CEB
U A
B C 00 01 11 10
00
01
1
0
1
0
0
1
0
1
CEB = U’C’ + UC
DC
U A
B C 00 01 11 10
00
01
1
0
1
0
1
0
1
0
141
Unit 12 Solutions
Present
State
Next State
MN =
AB 00 01 11 10
00 01 01 xx 10
12.33 (a) Present
State
JA KA
MN =
00 01 11 10
AB
Present
State
JB KB
MN =
00 01 11 10
AB
00 1x 1x xx 0x
01 x1 x1 x1 xx
Present
State
O0 O1
MN =
00 01 11 10
AB
00 00 00 01 10
12.33 (b)
12.34 Since the FFs are changing on the negative edge of the clock, the pulses must be concident with positive portions
of the clock. Assuming the clock is symmetrical, the FFs’ propagation delay must be less than half of the clock
period.
(a) The ring counter requires 8 stages: Q0, Q1, …, Q7 and Ti = (Clk)Qi for i = 0, 1, …, 7.
QU V
= 00
U V
= 01
U V
= 11
U V
= 10
12.35 (a) Q Q+U V
00 x 0
12.35 (b)
Q
Q+
A B
= 00
A B
= 01
A B
= 11
A B
= 10
0 0 0 1 1
12.35 (c)
Q
U V
A B
= 00
A B
= 01
A B
= 11
A B
= 10
0 x0 x0 11 11
142
Unit 12 Solutions
LA = B, MA = C; LB = A’, MB = A’ + C’; LC = A’B’,
MC = A’
12.37 (b)
(cont.)
A
B C 0 1
00
01
X
X
0
0
A
B C 0 1
00
01
X
X
X
X
A
B C 0 1
00
01
X
1
X
0
A
B C 0 1
00
01
0
1
X
X
A
B C 0 1
00
01
1
1
1
0
A
B C 0 1
00
01
1
X
0
X
A B C A+ B+ C+
0 0 0 1 0 0
0 0 1 0 0 0
0 1 0 X X X
12.37 (b) A+
A
B C 0 1
00
1
1
B+
A
B C 0 1
00
0
0
C+
A
B C 0 1
00
0
1
Q Q+ L M
0 0 0 1 X1
1 1
0 1 0 0 X0
}
12.37 (a)
Q
Q+
M F
= 00
M F
= 01
M F
= 11
M F
= 10
12.36 (a) Q Q+M F
00 11
12.36 (b)
Q
Q+
C D
= 00
C D
= 01
C D
= 11
C D
= 10
0 0 1 1 0
12.36 (c)
Q
M F
C D
= 00
C D
= 01
C D
= 11
C D
= 10
011 0x 0x 11
143
Unit 12 Solutions
A B C D A+ B+ C+ D+ JA KA JB KB JC KC JD KD
0 0 0 0 0 0 1 1 0 X 0 X 1 X 1 X
0 0 0 1 0 1 0 0 0 X 1 X 0 X X 1
0 0 1 0 0 1 0 1 0 X 1 X X 1 1 X
0 0 1 1 0 1 1 0 0 X 1 X X 0 X 1
0 1 0 0 0 1 1 1 0 X X 0 1 X 1 X
12.38 Using Karnaugh maps:
JA = A + BD + BC, KA = 0; JB = C + D, KB = C + D;
JC = D’, KC = D’; JD = 1, KD = 1
12.39 Clock
Cycle
Input
Data EnIn EnAd LdAc LdAd
Accumulator
Register
Addend
Register Bus Description
0 18 1 0 1 0 0 0 18 Input to accumulator
1 13 1 0 0 1 18 0 13 Input to addend
144
Unit 12 Solutions
12.40
(a), (b)
CE
En
Ck
A
CE
En
Ck
D
CE
En
Ck
C
CE
En
Ck
B
8 NAND gates 8
88 8 8
8
8
8
8
X Y
R
E
E
0
0
‘
E1
E2
12.40 (c) Call the values beginning in the A & D registers X and Y, respectively. We want C = X + Y = (X’Y’)‘. Invert using
M’ = 1 NAND M. To invert a value on the right side, in register C or D, we will need a 1 on the left side, in register A
or B. This can be accomplished using 1 = 0 NAND (anything.)
There are several solutions using different registers. Here is an example:
Clock
Cycle G0G1 E0 E1E2Description
Alternate three-cycle solution:
Use X + Y = X + X’Y = (X’ (X’Y)‘)‘
Clock
Cycle G0G1 E0 E1E2Description
1 0 0 0 1 1 1 NAND A = A’ = X’ → A
For bit reversal using the D inputs of the shift
register: Sh = 0, Ld = 1
12.41 (a)
Q3Q2Q1Q0
Ld
12.41 (b) Same as Figure 12-10 (b) on FLD p. 382, except
that for the “11″ input of each MUX, instead of SI,
Q3, Q2, or Q1, use Q0, Q1, Q2, or Q3, respectively.
Also, replace Sh with A and Ld with B.