Unit 9 Solutions
97
Unit 9 Problem Solutions
9.1 See FLD p. 741 for solution. 9.2 See FLD p. 741 for solution.
9.3 See FLD p. 742 for solution. 9.4 See FLD p. 742 and Figure 4-4 on FLD p.109.
9.5 y0 y1 y2 y3 a b c
0 0 0 0 0 0 0
1 0 0 0 0 0 1
y0 y1
y2 y300 01 11 10
00
0
0
0
0
00 01 11 10
00
0
1
0
1
y y
y y 0 1
2 3
00 01 11 10
00
0
1
1
1
y y
y y 0 1
2 3
9.6 See FLD p. 743 for solution. 9.7 See FLD p. 743 for solution.
9.8 See FLD p. 743-744 for solution. 9.9 The equations derived from Table 4-6 on FLD p.
111 are:
9.11 (a) F = C’D’ + BC’ + A’C → Use 3 AND gates
F’ = [C’D’ + BC’ + A’C]‘ = [C’ (B +D’) + CA’]‘
= [(C + B + D’) (A’ + C’)]‘
= B’C’D + AC → Use 2 AND gates
9.11 (b) F = A’B’ + C’D’ → Use 2 AND gates
F’ = (A’B’ + C’D’)‘
= (A + B)(C + D)
= AC + AD +BC +BD → Use 4 AND gates
9.13 B C
D E
00 01 11 10
0
0
0
0
Using Shannon’s expansion theorem:
F = ab’cde’ + bc’d’e + a’cd’e + ac’de’
= b’ (acde’ + a’cd’e + ac’de’) + b (c’d’e + a’cd’e + ac’de’)
Unit 9 Solutions
98
9.15
J0
J2
J1
I2
I1
I0
J0
I2
I1
I0
There are many solutions. For example:
9.14 (a)
a
0
g
9.14 (b)
a
c
b
9.16
16-to-1
I3
I2
I1
I0
Z
I7
I6
I5
I4
I8
16-to-1
Mux
I3
I2
I1
I0
Z
I7
I6
I5
I4
I11
I10
I9
I8
I15
I12
I13
I14
S4
S3S2S1S0
I3
I2
I1
I0
I7
I6
I5
I4
I8
I19
I18
I17
I16
I23
I22
I21
I20
I27
I26
I25
I24
I31
I28
I29
I30
16-to-1
Mux
I3
I2
I1
I0
Z
I7
I6
I5
I4
I11
I10
I9
I8
I15
I12
I13
I14
S3
S2
S1
S0
I2
I0
I6
I4
I10
I8
I12
I14
I18
I16
I22
I20
I26
I24
I28
I30
9.16
cont.
R = ab’h’ + bch’ + eg’h + fgh
= (ab’ + bc)h’+ (eg’ + fg)h
= [(a)b’ + (c)b]h’ + [(e)g’ + (f)g]h
Unit 9 Solutions
99
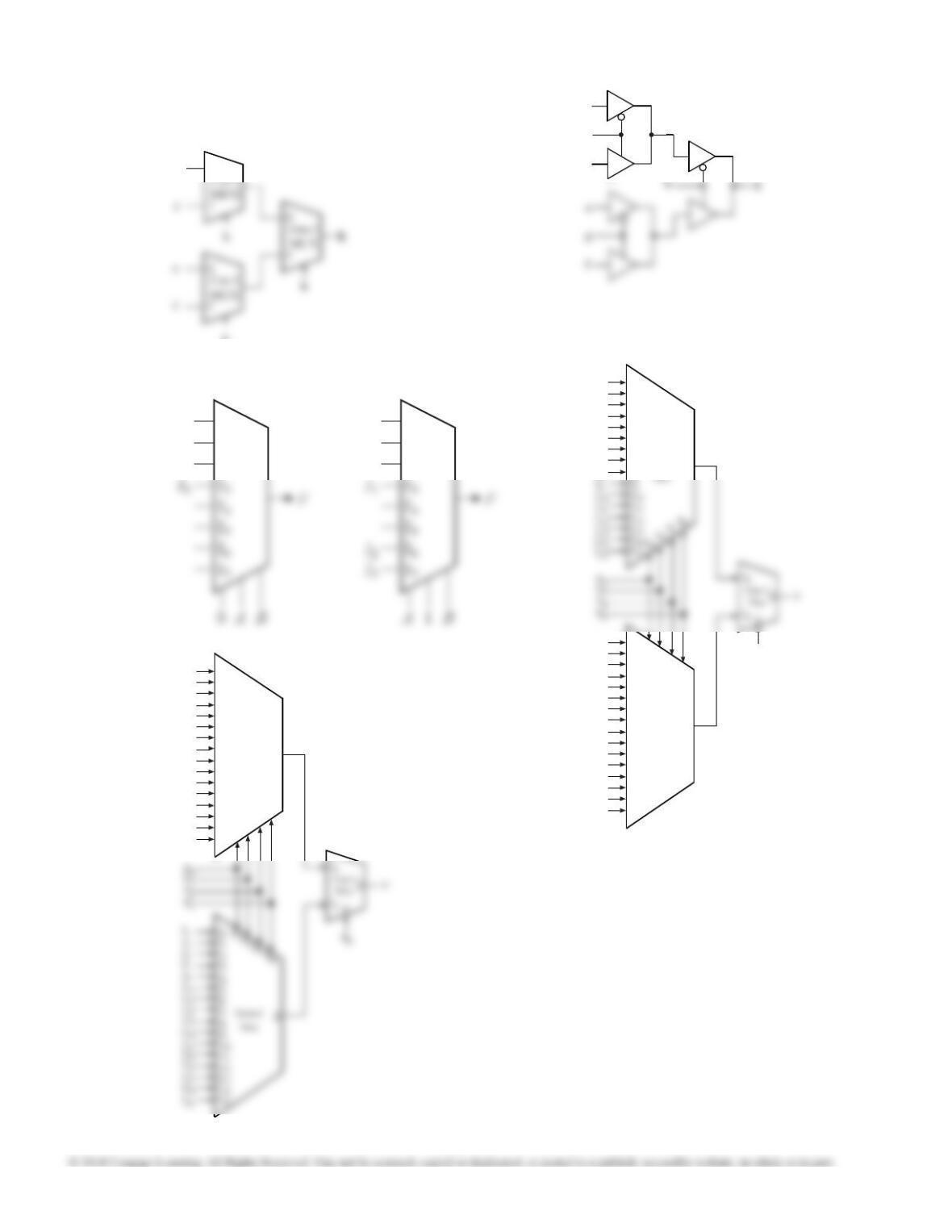
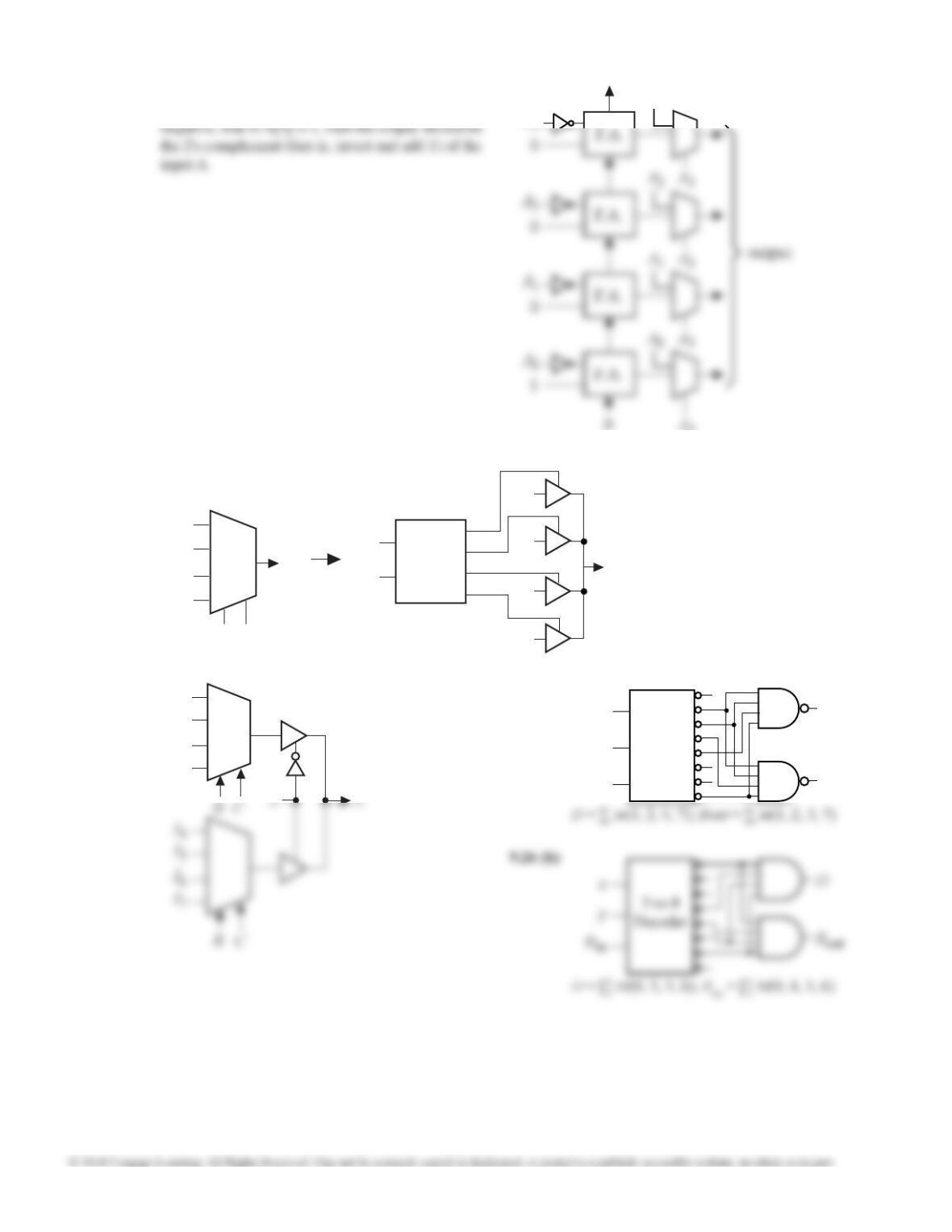
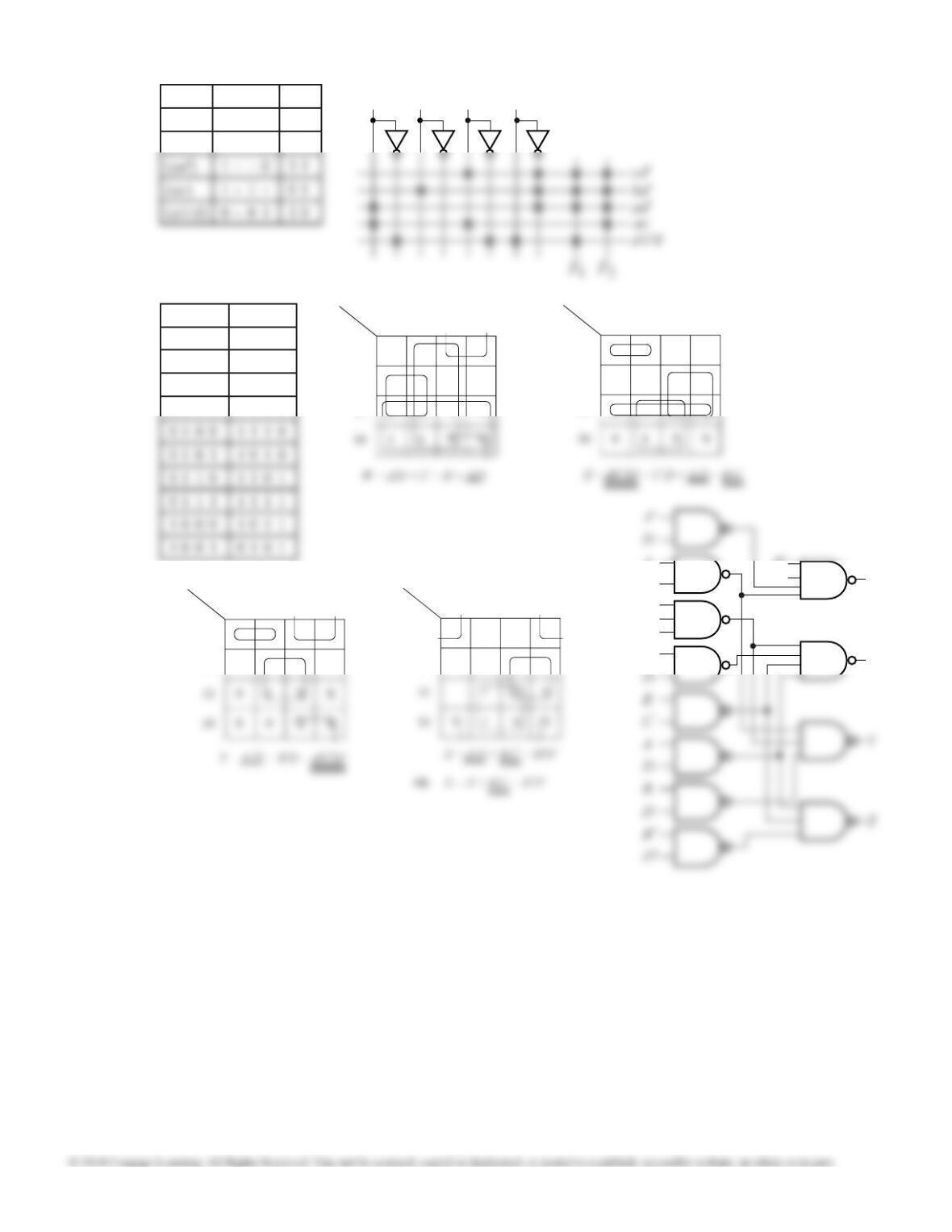
9.17 (c)
2-to-1
Mux
I0
I1
S
Z
S1
I0
I1
E
9.17 (a)
2-to-1
Mux
I0
I1
S
Z
S1
I0
I1
E
9.17 (b)
2-to-1
Mux
I0
I1
S
Z
S1
I0
I1
E
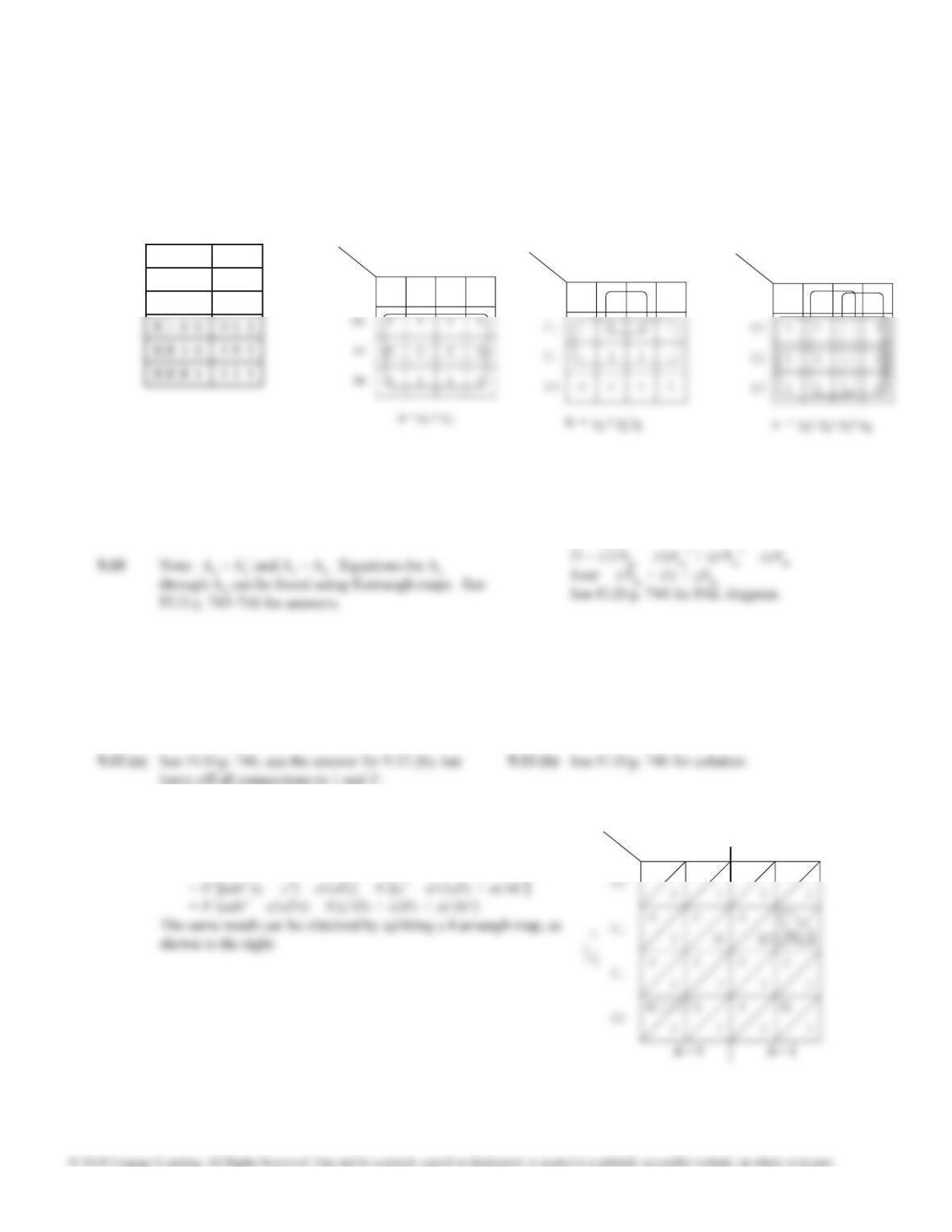
9.18
m0
4 – to – 10
A
s3
m1
m2
m3
f
Since the decoder outputs are negative, NAND
gates are required. The excess-3 outputs are
S m(5,6,7,8,9), S m(1,2,3,4,9), S m(0,3,4,7,8), and
S m(0,2,4,6,8) so four 5-input NAND gates are
needed with inputs corresponding to the minterms
of the excess-3 outputs.
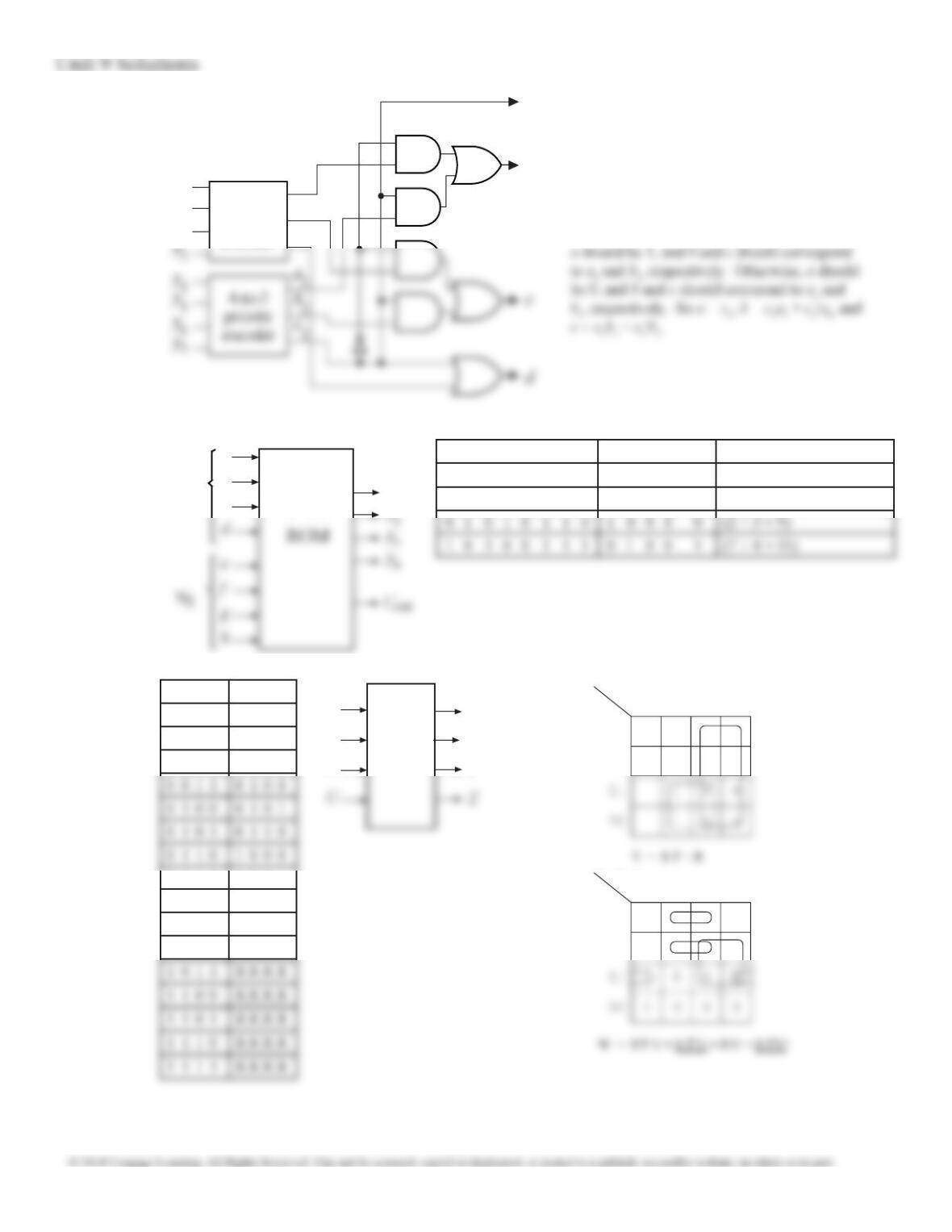
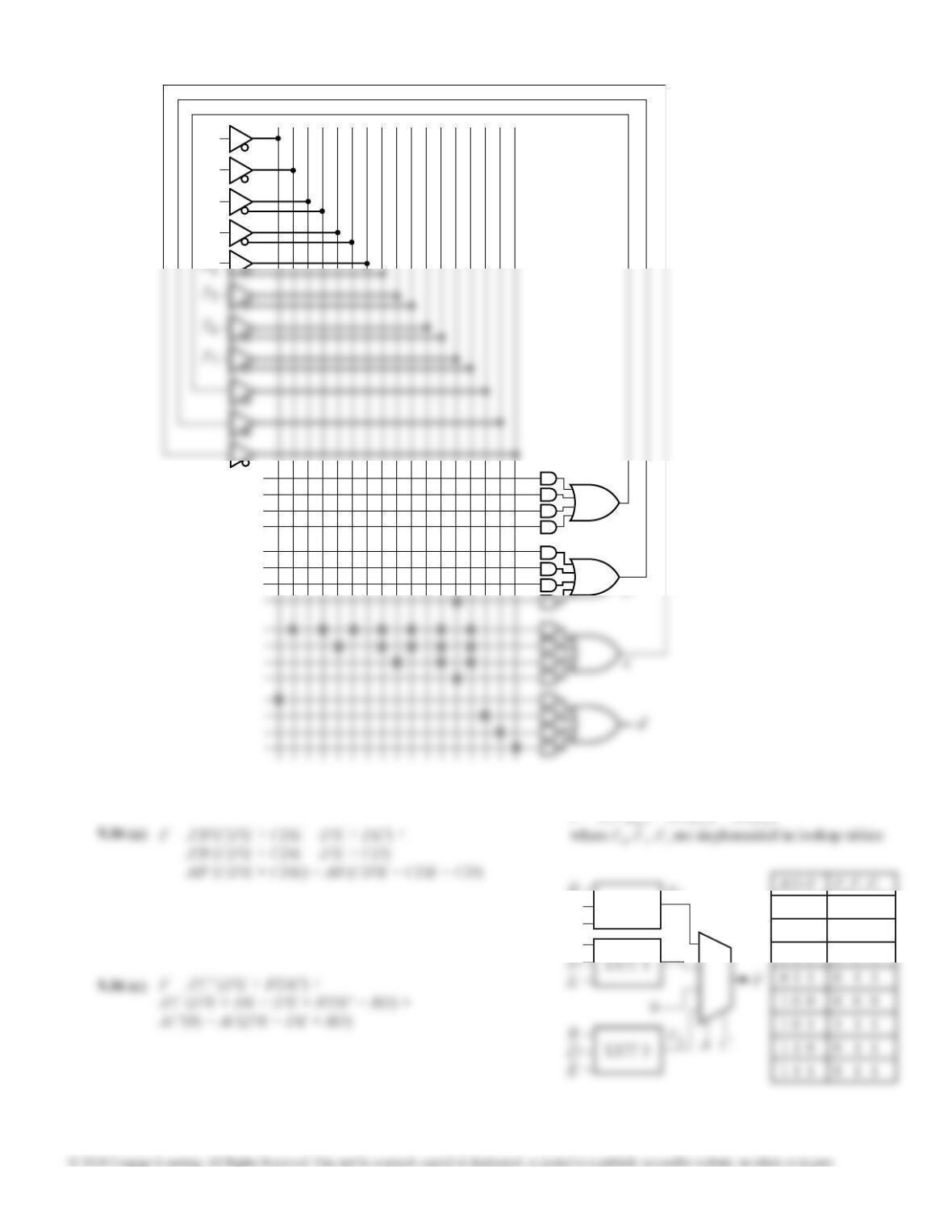
Using S1 = w and S0 = z, I0 = x, I1 = 1, I2 = y and
I3 = 0 which does not require any gates.
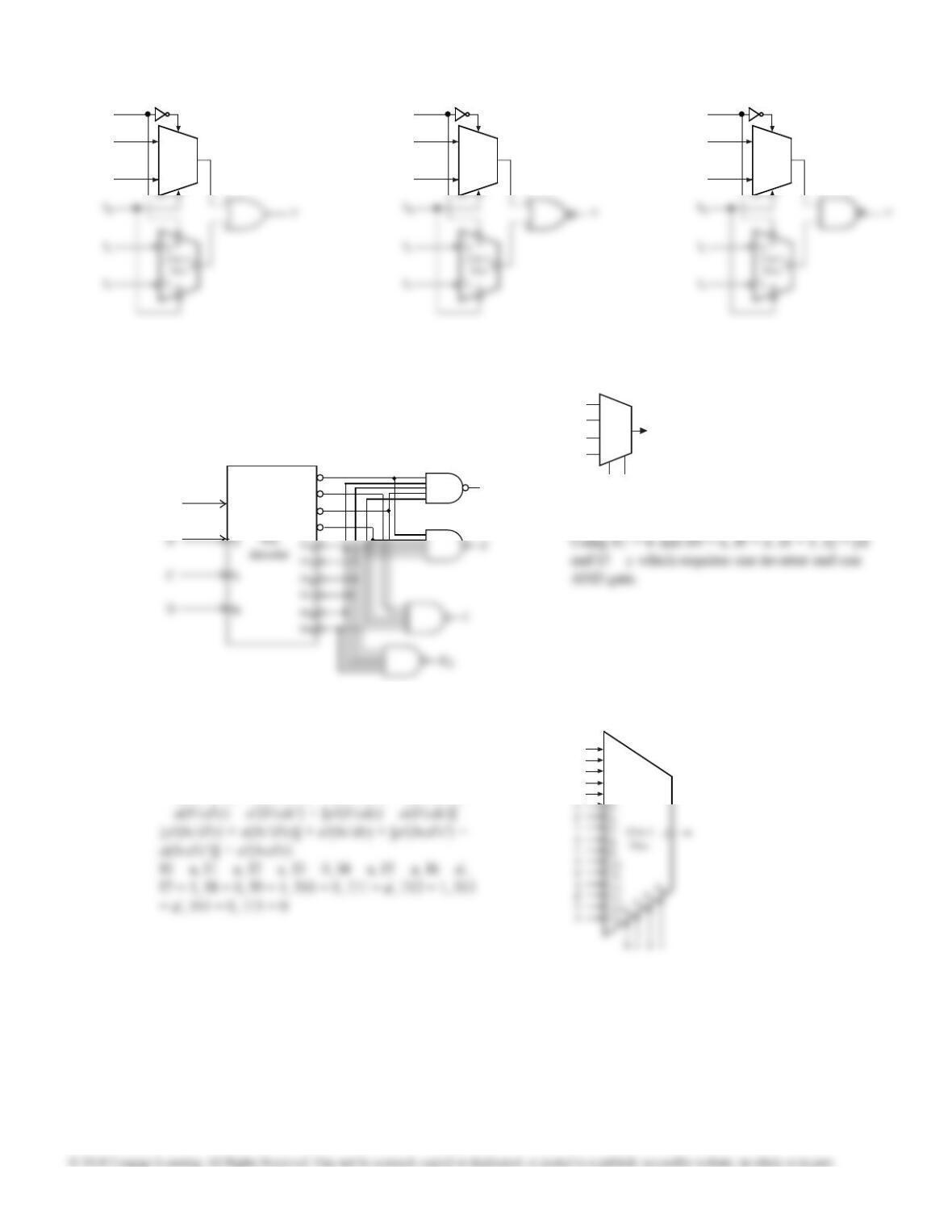
9.19
x
1
y
0
w
F
z
Other answers: Using S1 = w and S0 = y, I0 = x, I1
= z, I2 = 0 and I3 = z’ which requires one inverter.
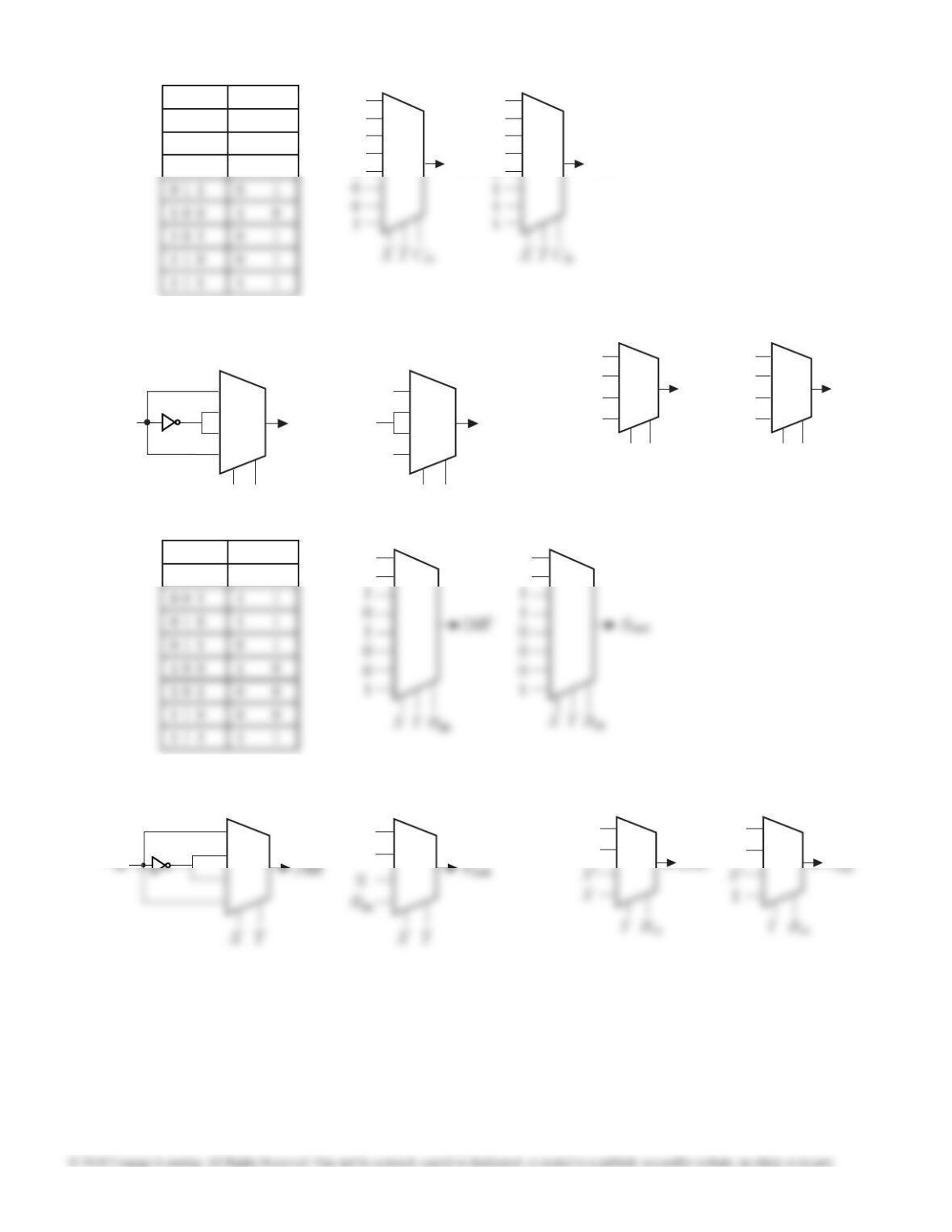
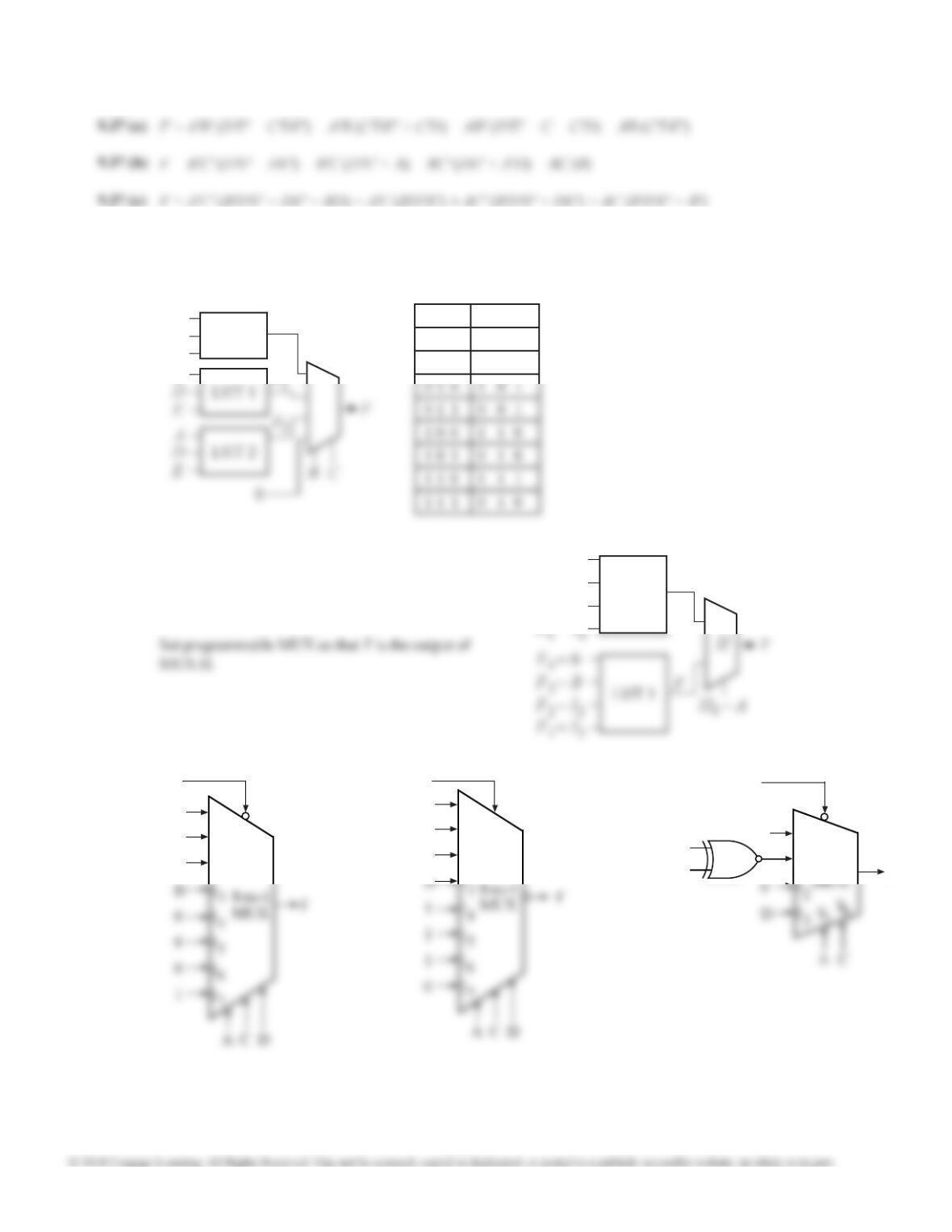
9.20
I3
I2
I1
I0
I4
a
a
a
0
a
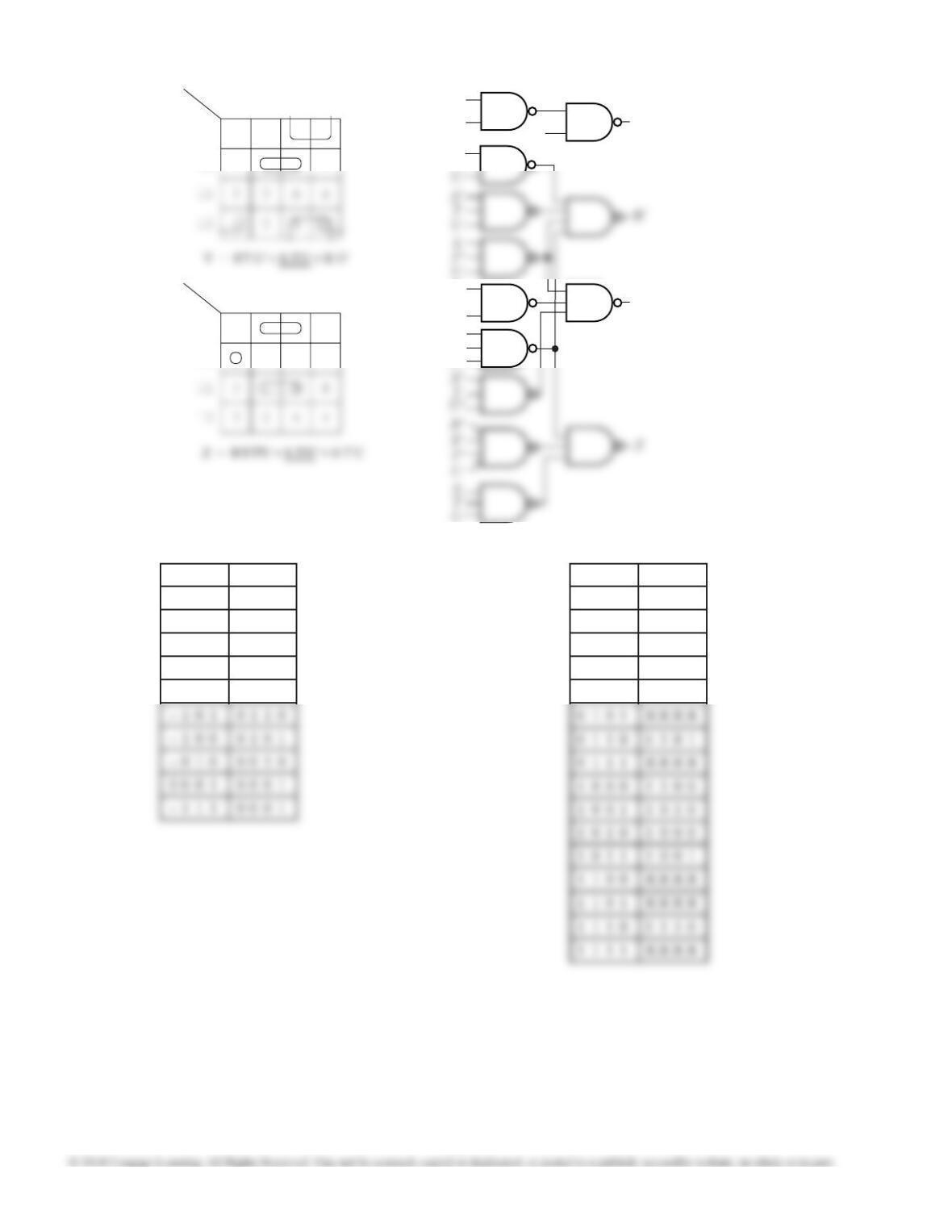
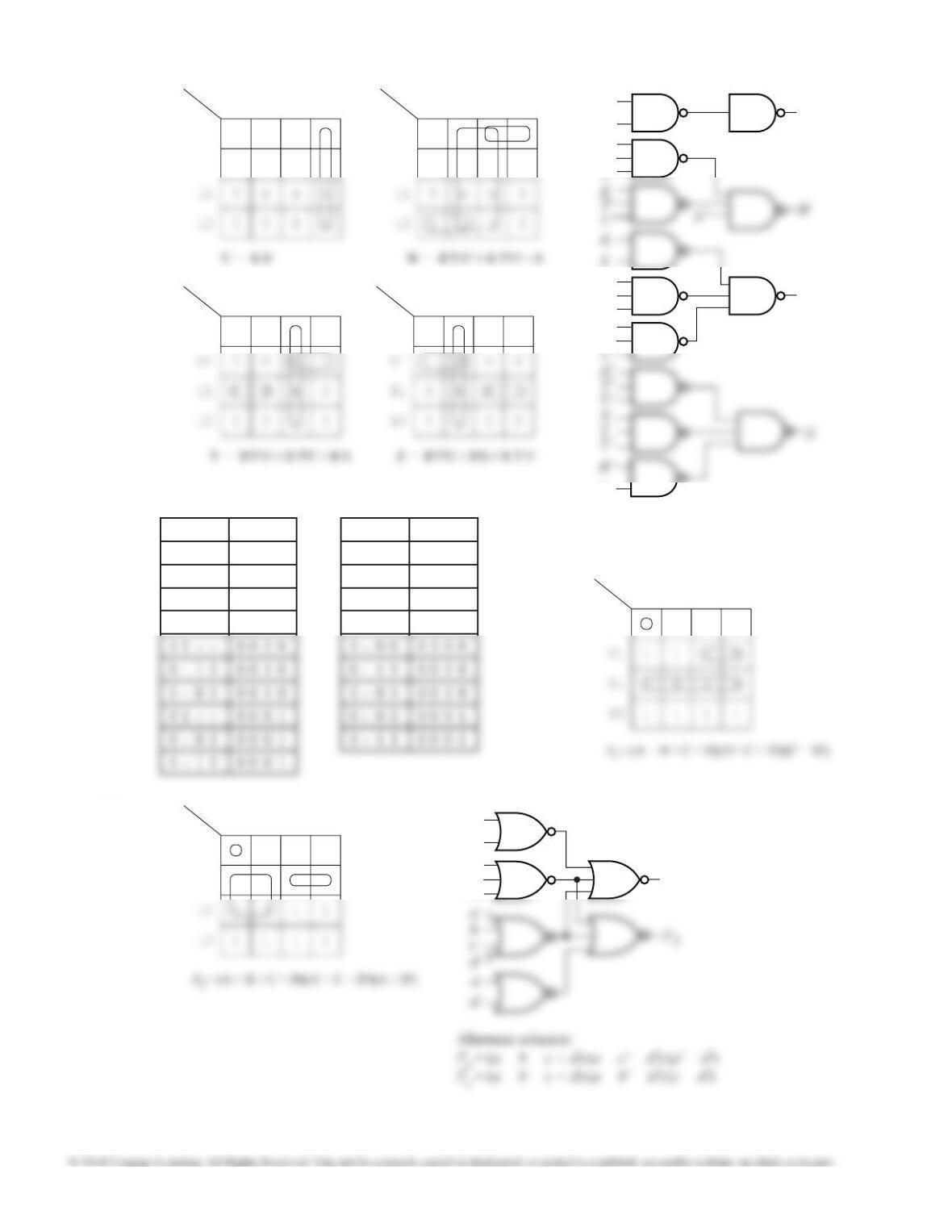
f (a, b, c, d, e) = a’b’cde’ + a’b’cde + a’bc’d’e +
a’bc’de + a’bcd’e’ + a’bcd’e + ab’c’d’e’ + ab’c’d’e +
ab’c’de’ + ab’cd’e’ + ab’cd’e + ab’cde + abc’d’e +
abcd’e’
= a(b’c’d’e’) + a(b’c’d’e) + a(b’c’de’) + a(b’cd’e’)
Unit 9 Solutions
100
Bin
B’
in
Bin
1
9.22 (b) 9.22 (c)
X
X’
0
X’
Bout
x y cin Sum Cout
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0
1
1
0
1
Sum
0
0
0
1
0
Cout
C’in
X Y
Sum
0
Cin
1
X Y
Cout
Cin
X
X’
X’
X
Y
Sum
Y
Cout
Cin Cin
0
X
X
1
9.21 (a)
9.21 (b) 9.21(c)
9.22 (a) x y bin Diff Bout
0 0 0 0 0
0
1
0
1
Unit 9 Solutions
101
9.23 For a positive number A, |A| = A and for a negative
number A, |A| = −A. Therefore, if the number is
A3
A3
9.24
I0
I1
I2
I3
m0
m1
m2
m3
Z
A
B
2-to-4
decoder
I0
I1
I2
I3
A B
Z
9.25 I0
I1
I2
I3
9.26 (a)
3-to-8
Decoder
D
Bout
x
y
Bin
102
9.27
4-to-2
priority
encoder
y0
y1
y2
a
b
a1
b1
c1
9.28
3
a
b
c
S
2 x 5
N1
8
a b c d e f g h S3 S2 S1 S0 Cout Meaning
0 0 0 0 0 0 0 0 X X X X X (0000 is a not valid input)
0 0 1 1 0 0 1 1 0 0 1 1 0 (0 + 0 = 0)
9.29 (a) R S T U V W Y Z
0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 1
0 0 1 0 0 0 1 0
0 1 1 1 1 0 0 1
1 0 0 0 1 0 1 0
1 0 0 1 1 1 0 0
1 0 1 0 X X X X
R
S
T
V
W
Y
2 x 4
ROM
4
9.29 (b) R S
T U 00 01 11 10
00
01
1
1
X
X
R S
T U 00 01 11 10
00
01
0
0
1
1
0
1
X
X
If any of the inputs y0 through y7 is 1, then d of the
8-to-3 decoder should be 1. But in that case, c1
or c2 of one of the 4-to-2 decoders will be 1. So
d = c1 + c2.
If one of the inputs y4, y5, y6, and y7 is 1, then
Unit 9 Solutions
103
9.29 (b)
(cont.) R S
T U 00 01 11 10
00
01
0
0
0
1
1
0
X
X
R S
T U 00 01 11 10
00
01
0
1
1
0
0
0
X
X
T
S
R
U’
T’
S
U’
Y
V
R’
R
U
9.29 (c) R S T U V W Y Z
– 1 1 – 1 0 0 0
1 0 0 – 1 0 0 0
1 – – 0 0 0 1 0
1 – – 1 0 1 0 0
– 0 1 1 0 1 0 0
9.30 (a) R S T U V W Y Z
0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 1
0 0 1 0 0 1 0 0
0 0 1 1 0 0 1 0
0 1 0 0 X X X X
Unit 9 Solutions
104
9.30 (c) R S T U V W Y Z
1 0 – – 1 0 0 0
0 1 – – 0 1 0 1
1 1 – – 0 1 1 0
0 – 1 0 0 1 0 0
9.31 (a) A B
C D 00 01 11 10
00
0
1
1
1
9.31 (a)
(cont.)
A B
C D 00 01 11 10
00
01
0
0
1
0
1
0
1
0
c’
d’
a’
c
d
F1
R S T U V W Y Z
1 0 – – 1 0 0 0
– 1 – – 0 1 0 0
0 – 1 0 0 1 0 0
1 – 0 0 0 1 0 0
or
R S
T U 00 01 11 10
00
01
0
0
X
X
1
0
X
X
R S
T U 00 01 11 10
00
0
X
0
X
R S
T U 00 01 11 10
00
0
X
0
X
S’
T
R’
R
S
T
R’
U
T’
R
Y
V
9.30 (b) R S
T U 00 01 11 10
00
01
0
0
X
X
1
1
X
X
Unit 9 Solutions
105
db c
a
9.31 (b) a b c d F1 F2
(cd’) – – 1 0 1 1
(bd’) – 1 – 0 1 1
9.32 (a) A B C D W X Y Z
0 0 0 0 0 1 1 1
0 0 0 1 1 0 0 0
0 0 1 0 1 0 0 1
0 0 1 1 1 1 0 0
A B
C D 00 01 11 10
00
01
11
0
1
1
1
1
1
1
0
X
X
X
X
A B
C D 00 01 11 10
00
01
11
1
0
1
1
0
1
0
1
X
X
X
X
A B
C D 00 01 11 10
00
01
1
1
1
X
X
A
D’
C
C’
A’
D’
X
W
C’
B’
A B
C D 00 01 11 10
00
01
1
0
1
1
1
0
X
X
Unit 9 Solutions
106
9.32 (b) a b c d W X Y Z
– 1 – – 1 0 0 0
– – 1 – 1 0 0 0
0 – – 1 1 0 0 0
1 – – 0 1 0 1 0
9.32 (c)
db c
a
9.33 (a)
db c
a
xx
ab’d
x
1
2
x
3
a b c d f1 f2 f3
1 0 – 1 1 0 0
– 0 1 1 1 0 1
0 1 – 0 1 0 0
x y z f1 f2 f3
0 1 1 1 1 0
0 1 0 1 0 1
9.33 (b)
See solution for 7.10
See solution for 7.41 9.33 (c) Because a PLA works with a sum-of-products
expression, see solution for 7.43(b), not (a).
a b c d f1 f2
1 – 0 – 1 0
y z
x
x
x
xx
xx
x’yz
x’yz’
x
x
xx
db c
a
x
ac’
x
x
Unit 9 Solutions
107
x x
x
xx
x xx
x
A
B
C
X1
xxx
x x x x
I0
I7
Z = I0A’B’C’ + I1A’B’C + I2A’BC’ + I3A’BC + I4AB’C’ + I5AB’C + I6ABC’ + I7ABC
= X1A’ + X2A where X1 = I0B’C’ + I1B’C + I2BC’ + I3BC and X2 = I4B’C’ + I5B’C + I6BC’ + I7BC
9.34
Note: Unused inputs, outputs, and
wires have been omitted from this
diagram.
For an 8-to-3 encoder, using the truth table given in
FLD Figure 9-16, we get
a = y4 + y5 + y6 + y7
9.35
Unit 9 Solutions
108
Note: Unused inputs, outputs,
and wires have been omitted
from this diagram.
y2
y4
y3
x
x x
x
x
x
x
y1
y0
a
x
x
x x x
x x x x
x
9.35
(cont.)
9.36 F = CD’E + CDE + A’D’E + A’B’DE’ + BCD
F = B’C’ (A’D’E + A’DE’) +
B’C (D’E +DE + A’D’E + A’DE’) +
BC’ (A’D’E) + BC (D’E + DE + A’D’E + D)
9.36 (b)
LUT 0
D
E
B
B
F0
F1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 0 1 1 0
9.36 (d) Use the expansion about A and C
Unit 9 Solutions
109
9.37 F = B’D’E’ + AB’C + C’DE’ + A’BC’D
In this case, use the expansion about B and C to implement the function in 3 LUTs:
F = B’C’(F
0) + B’C(F
1) + BC’(F
2) + BC(0)
Here we use the LUTs to implement F0, F1, F2 which are functions of A, D, E
A D E F0 F1 F2
0 0 0 1 1 0
0 0 1 0 0 0
LUT 0
D
E
A
A
F0
F1
LUT 0
G = I
G = 0
G
G = B
4
3
2
0
9.38 For a 4-to-1 MUX:
Y = A’B’I0 + A’BI1 + AB’I2 + ABI3
= A’ (B’I0 + BI1) + A(B’I2 + BI3)
= A’G + AF, where G = B’I0 + BI1; F = B’I2 + BI3
B’
1
1
E
I2
I1
I0
0
9.39 (a)
B
0
0
E
I2
I1
I0
1
9.39 (b)
f
1
4-to-1
0
I0
I1
E
D
B
9.39 (c)
9.40 Same answer as 9.39 except connect E to the enable
input in parts (a) and (c) and E’ in part (b).
Unit 9 Solutions
110
LUT 0
a
e
b
F = a’ + ac’d’ + b’cd’ + ad
9.41 (a)
9.41 (b)
9.41 (c) a b c e g
0 1 0 1 1
0 1 1 1 1
1 0 0 1 1
F = cd’ + ad’ + a’b’cd’+ bc’
= d’(c + a + bc’ ) + d(a’ b’c+ bc’)
= d’(e) + d(g)
9.42 (a) 9.42 (c) a b c e g
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 1 0
1 0 0 1 0
Same as 9.41 (b).
9.42 (b)
0 1 0 1 1
0 1 1 1 1
1 0 0 0 1
1 0 1 0 0
1 1 0 1 1
1 1 1 0 1
Same as 9.41 (b).
9.43 (b)
f = b′(ac′ + ac + a′c′). b′ must be connected to
w. If s = a, t = c, then connect y0, y2 and y3 to a
3-input OR-gate. If s = c, t = a, then connect y0, y1
and y3 to a 3-input OR-gate.
9.44 (a)
No. The outputs are y0 = s′t′w, y1 = s′tw, y2 =
st′w and y3 = stw so any function realized by ORing
9.44 (b)
If a NOR-gate is connected to some of outputs of
M and it realizes the function f, then f′ is the OR of
the minterms from M. For the function of Part (a),
f′ = (a′ + b)(b + c) = b + a′c = a′bc′ + a′bc + abc′ +
abc + a′b′c. f′ contains ve minterms and, hence,
9.44 (c)
Unit 9 Solutions
111
Z3 = A, Z2 = A′B, Z1 = A′B′C and Z0 = A′B′C′D
9.45 The decoder outputs are Y0 = A′B′, Y1 = A′B, Y2 =
AB′, Y3 = AB. The mux outputs are
f = I0′C′D′ + I1′C′D + I2′CD′ + I3′CD. So
f(A,B,C,D) = Y0′C′D′ + Y1′C′D + Y2′CD′+ Y3′CD
9.46 (a)
The decoder outputs are minterms of A and B
active low: Y0 = A′B′, Y1 = A′B, Y2 = AB′, Y3 = AB.
9.46 (b)
Let c0 = 0 and ci = 0(1) indicate that A > B (A <
B) in bits 0, …, i, then ci+1 = ciai′ + cibi + ai′bi.
9.47 (a) It is not possible to determine the output of Mi
between the three cases, A > B, A = B and A < B so
there must be a second line between the modules.
9.47 (c)
For c0 = 1, the ci are the carries between adder
stages for A + (-B).
9.47 (b)
C
in Sum
X
Sum = (X ⊕ Y) ⊕ Cin and
Cout = X′YCin + XY′Cin + XYC′in + XYCin
9.48 (a)
xi
di
bi
yi
di = (xi ⊕ yi) ⊕ bi and
bi+1 = xi′yi′bi + xi′yibi′ + xi′yibi + xiyibi
= (xi′yi′ + xiyi)bi + xi′yi
9.49 (a)
Unit 9 Solutions
112