Unit 7 Solutions
Unit 7 Problem Solutions
a b
c d 00 01 11 10
00
01
0
0
1
0
1
1
0
0
a b
c d 00 01 11 10
00
01
0
0
1
0
1
1
0
0
f = a’b (c + d’) + ab’ (c’ + d’)
7.1 (a)
Beginning with a minimum product of sums
solution, we can get
Beginning with the minimum sum of products
solution, we can get
F = (AD + B) (E’ + C’) + A’D’E’
F = (E + FG) [A + B (C + D)]
7.1 (b)
AC’D + ADE’ + BE’ + BC’ + A’D’E’
= E’ (AD + B) + A’D’E’ + C’ (AD + B)
7.2 (a)
7.2 (b) AE + BDE + BCE + BCFG + BDFG + AFG
= AE + AFG + BE (C + D) + BFG (C + D)
f = (a + b) (a’ + b’) (d’ + ac’ + a’c))
2
2
Unit 7 Solutions
72
a’
NOR-NOR
a
AND-NOR NAND-AND
a
OR-AND
a’
A B
C D 00 01 11 10
00
01
0
0
0
1
0
1
0
1
A B
C D 00 01 11 10
00
01
0
0
0
1
0
1
0
1
NAND-NAND OR-NAND
NOR-OR
AND-OR
7.3 F (a, b, c, d)n = a’bd + ac’d or d (a’b + ac’) = d (a + b) (a’ + c’)
You can obtain this equation in the product of sums form using a Karnaugh map, as shown below:
7.4
A B
C D 00 01 11 10
00
01
0
0
0
1
0
0
1
1
F = BC’ (A + D) + AB’C
2 3
3
2
F (A, B, C, D) = ∑ m(5, 10, 11, 12, 13) F = ABC’ + BC’D + AB’C = BC’ (A + D) + AB’C
73
7.5 A B
C D 00 01 11 10
00
01
0
1
0
1
1
0
0
0
7.6
B
CD’ A
Z = ABC + AD + C’D’
= A (BC + D) + C’D’
For the solution to 7.8, see
FLD p. 738.
7.9 a b
c d 00 01 11 10
00
01
1
1
1
a b
c d 00 01 11 10
00
01
1
1
1
6 gates
7.8
7.10
a b
c d 00 01 11 10
00
01
1
1
a b
c d 00 01 11 10
00
01
1 1
1
a b
c d 00 01 11 10
00
01
f1 (A, B, C, D) = ∑ m(3, 4, 6, 9, 11)
f2 (A, B, C, D) = ∑ m(2, 4, 8, 10, 11, 12)
f3 (A, B, C, D) = ∑ m(3, 6, 7, 10, 11)
Unit 7 Solutions
7.12 A B
C D 00 01 11 10
00
01
0
0
0
1
1
1
0
1
A B
C D 00 01 11 10
00
01
0
0
0
0
1
1
0
1
7.13 (a) Using F = (F’)’ from Equations (7-23(b)), p. 206:
f1 = [(A’BD)‘ (ABD)‘ (AB’C’)‘ (B’C)‘]‘; f2 = [C’ (A’BD)‘]‘; f3 = [(BC)‘ (AB’C’)‘ (ABD)‘]‘
A’
B
D
A
B’
A B
C D 00 01 11 10
00
01
0
0
0
1
0
0
0
0
7.11 a b
c d 00 01 11 10
00
01
0
0
0
0
1
1
0
0
a b
c d 00 01 11 10
00
01
1
1
0
1
1
1
0
0
8 gates
7.13 (b) Using F = (F’)’ from Equations derived in problem 7.12:
f1 = [(A + B + C)‘ + (B’ + D)‘]‘
f2 = [(A + B + C)‘ + (B’ + C + D)‘ + (A’ + C)‘]‘
Unit 7 Solutions
75
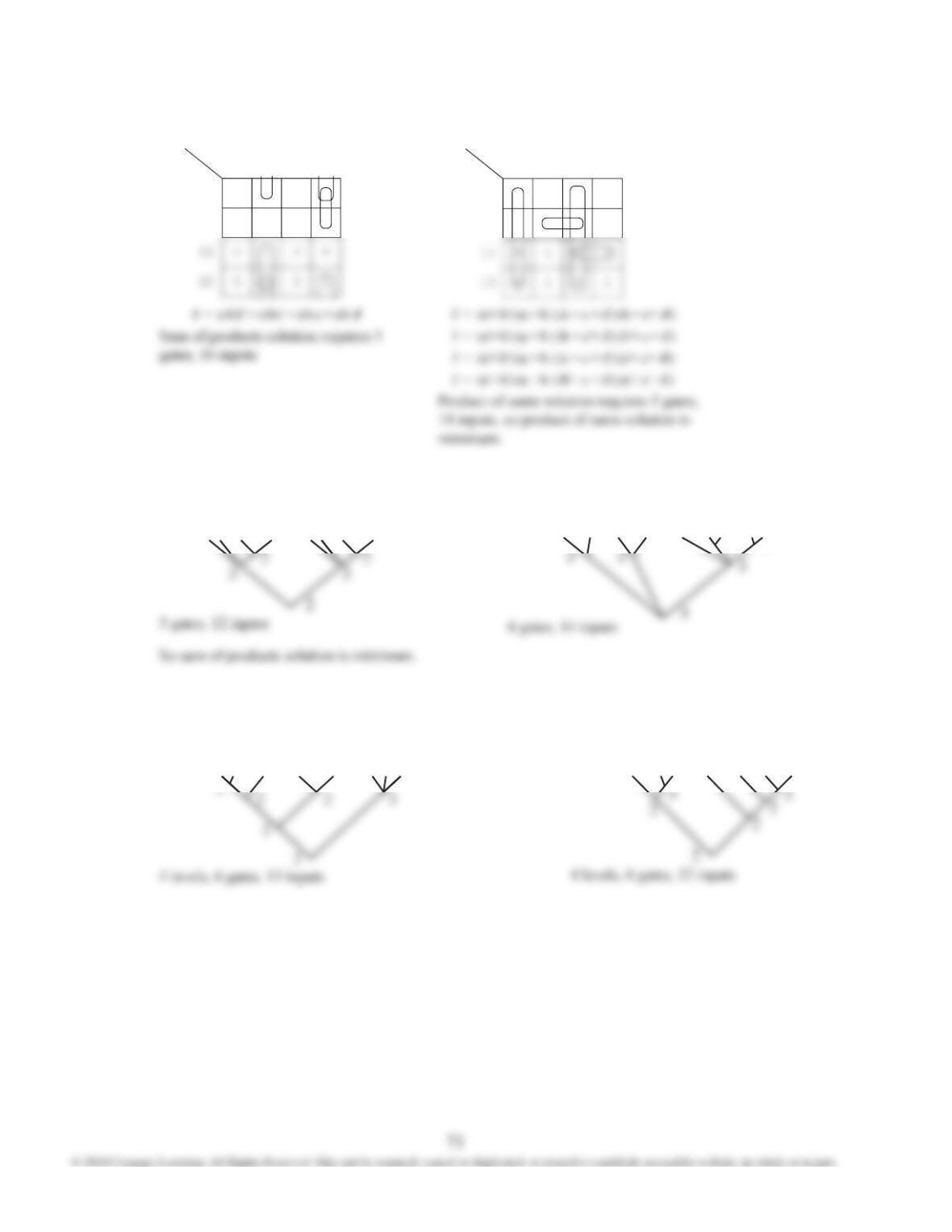
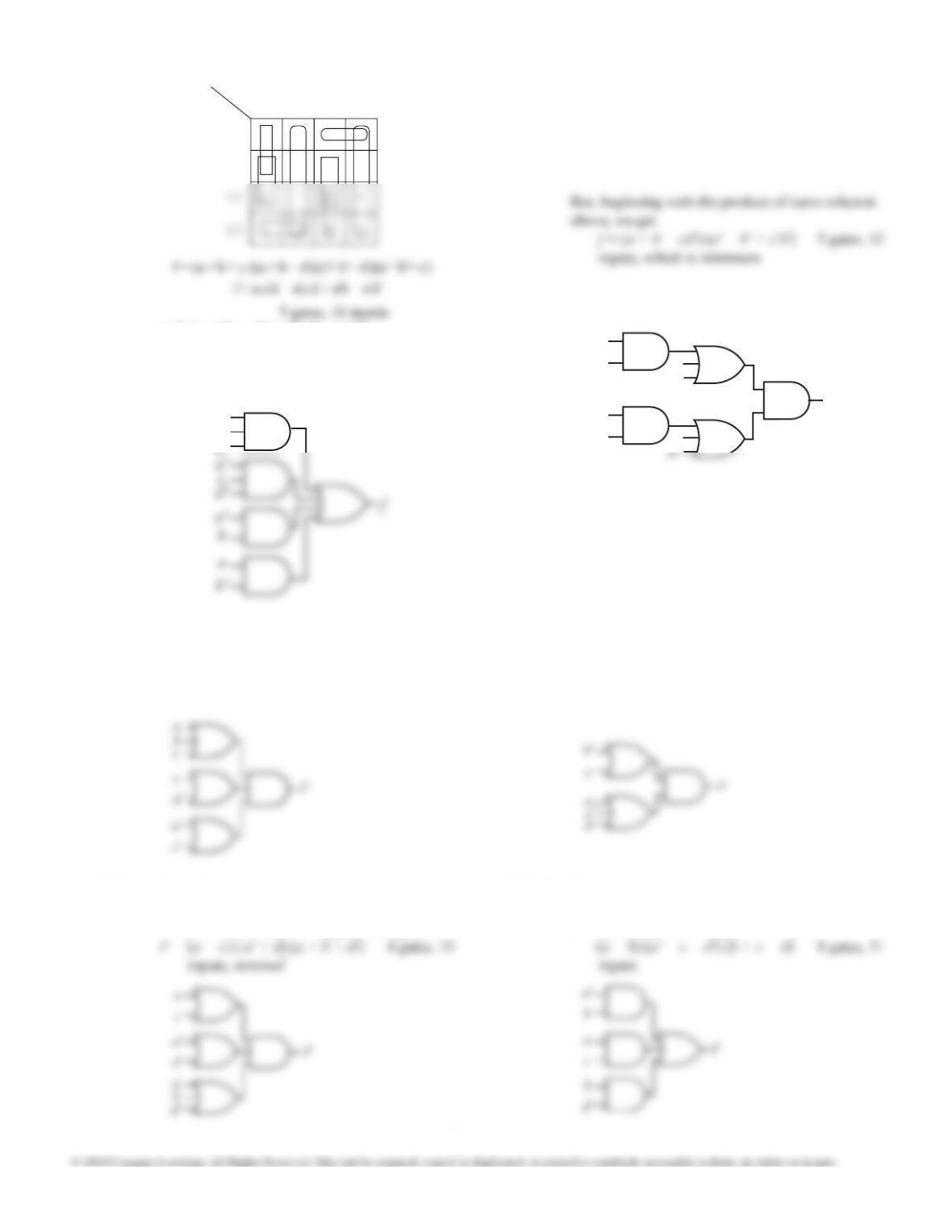
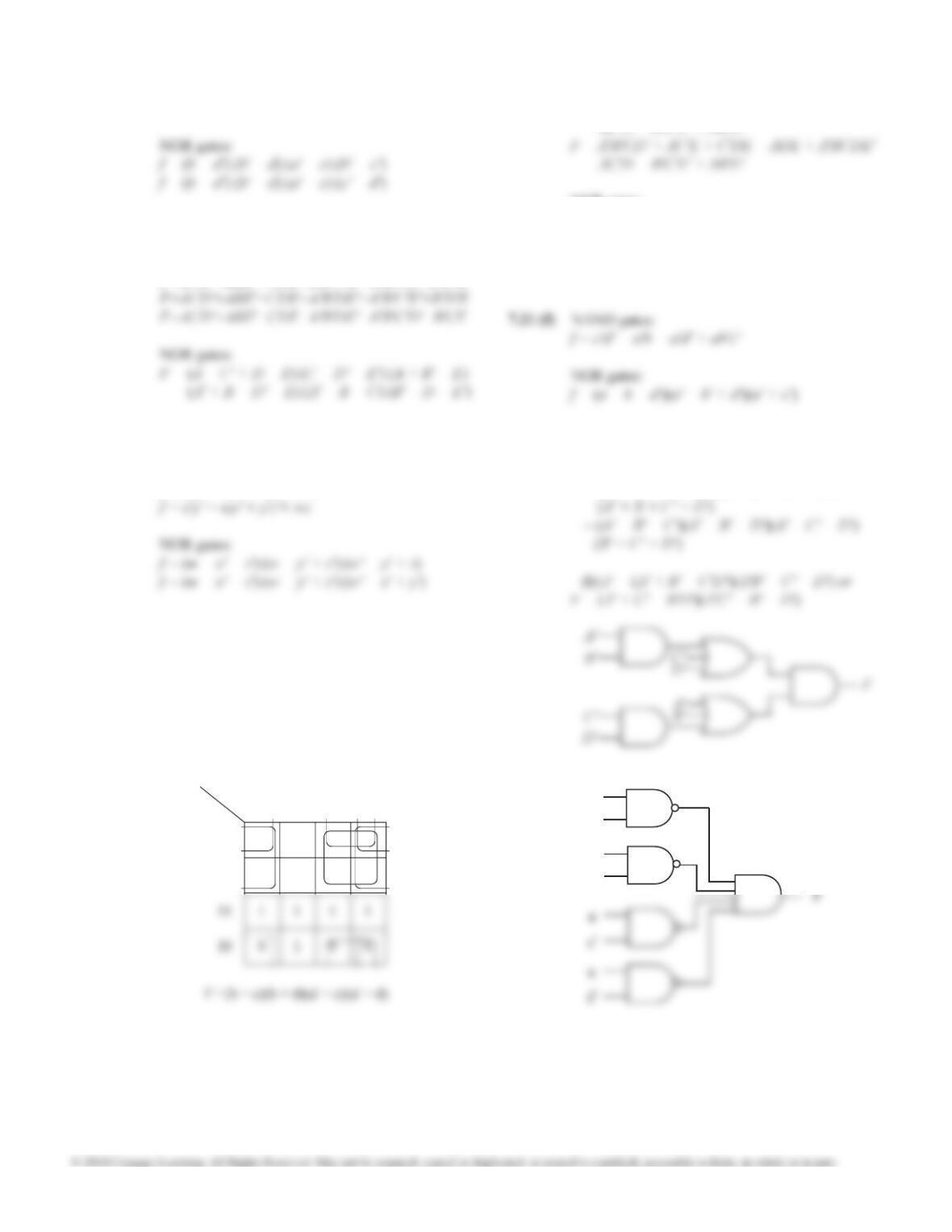
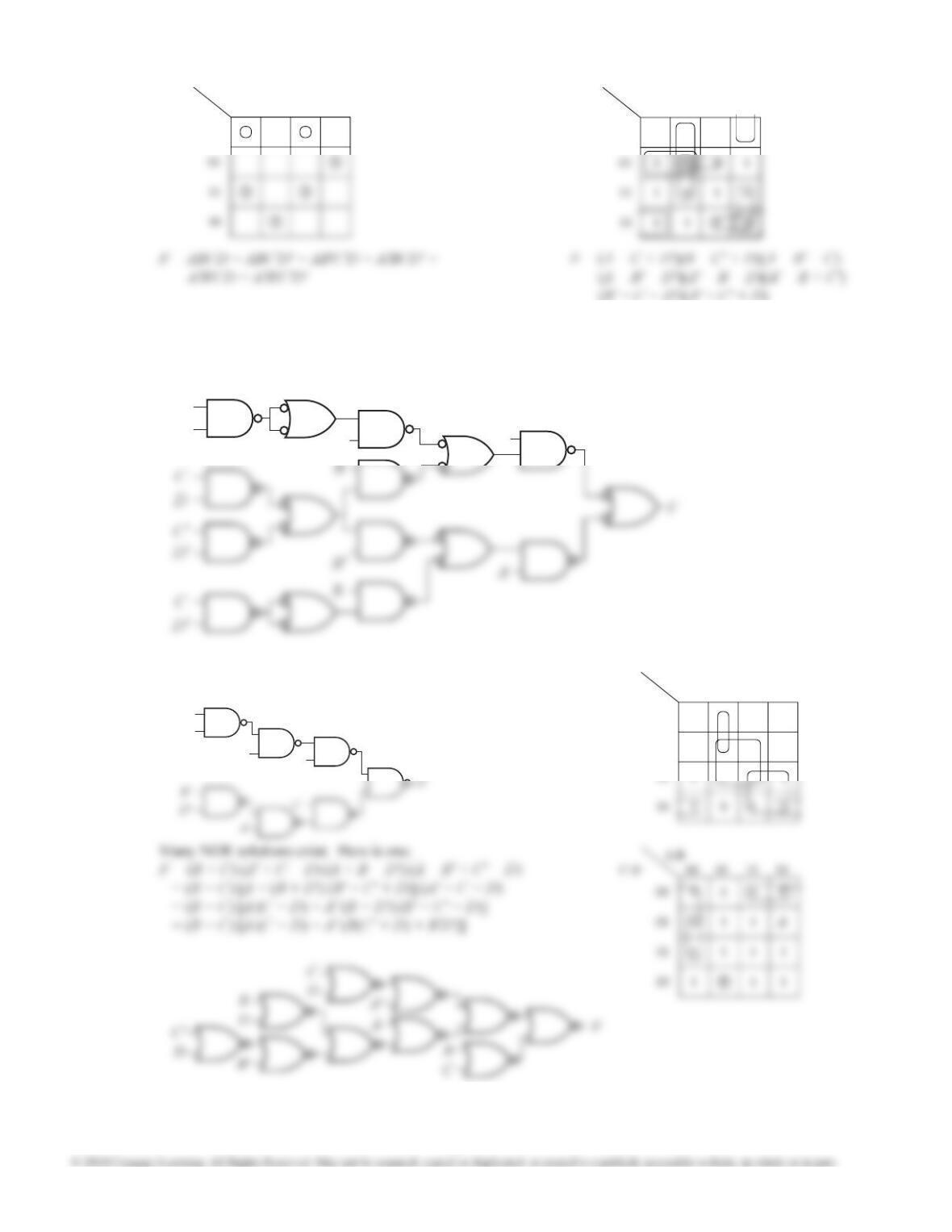
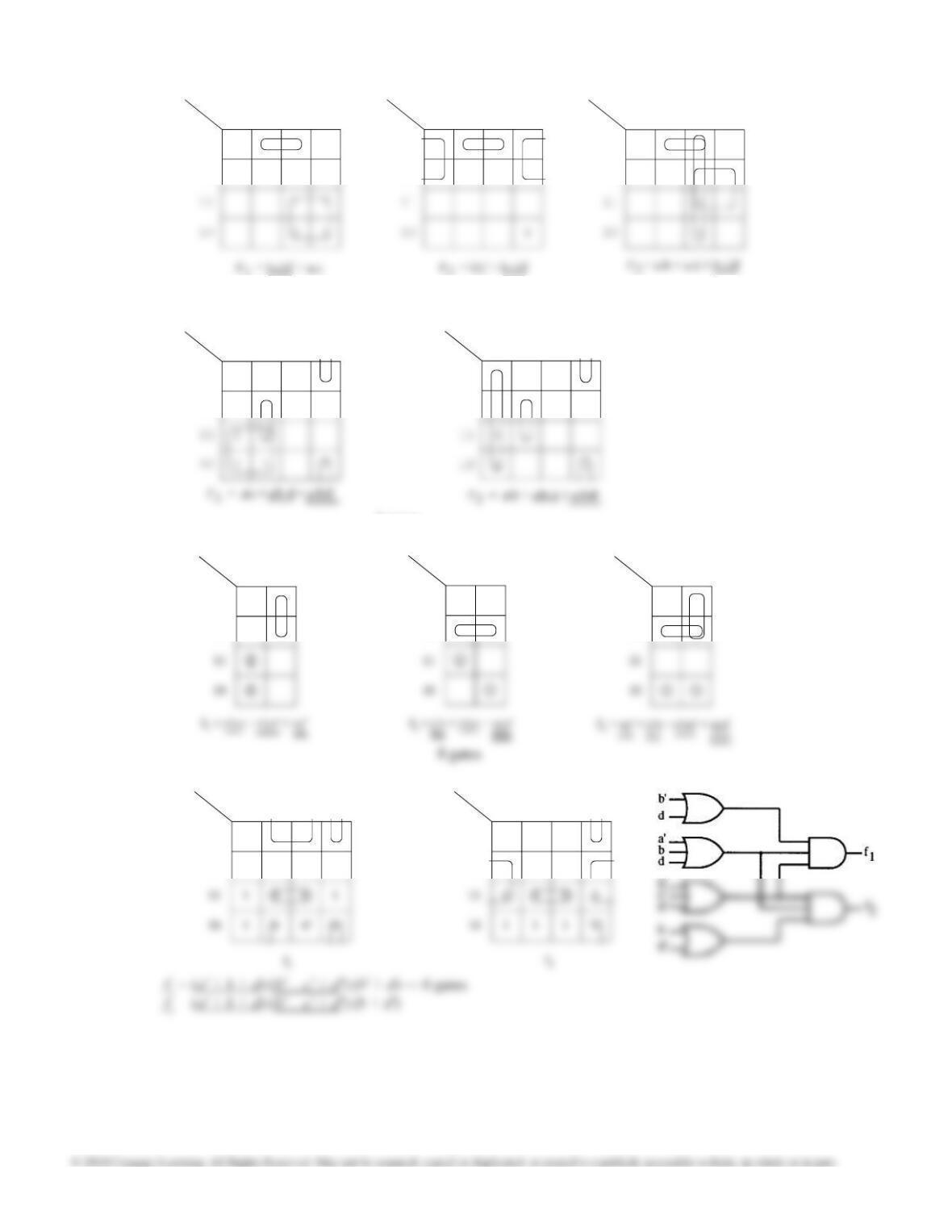
7.14 (a)
a
c’
and f = a’b + ab’ + b’cd’ + ac’d’
f = a’b + ab’ + a’cd’ + bc’d’
(two other minimun solutions)
5 gates, 14 inputs minimal
7.14 (b) Beginning with the sum of products solution, we
get
f = a’b + ab’ + d’ (a’c + ac’)
= a’b + ab’ + d’ (a’ + c’) (a + c) — 6 gates,
14 inputs
d’
a’
c
d’
a’
b
f
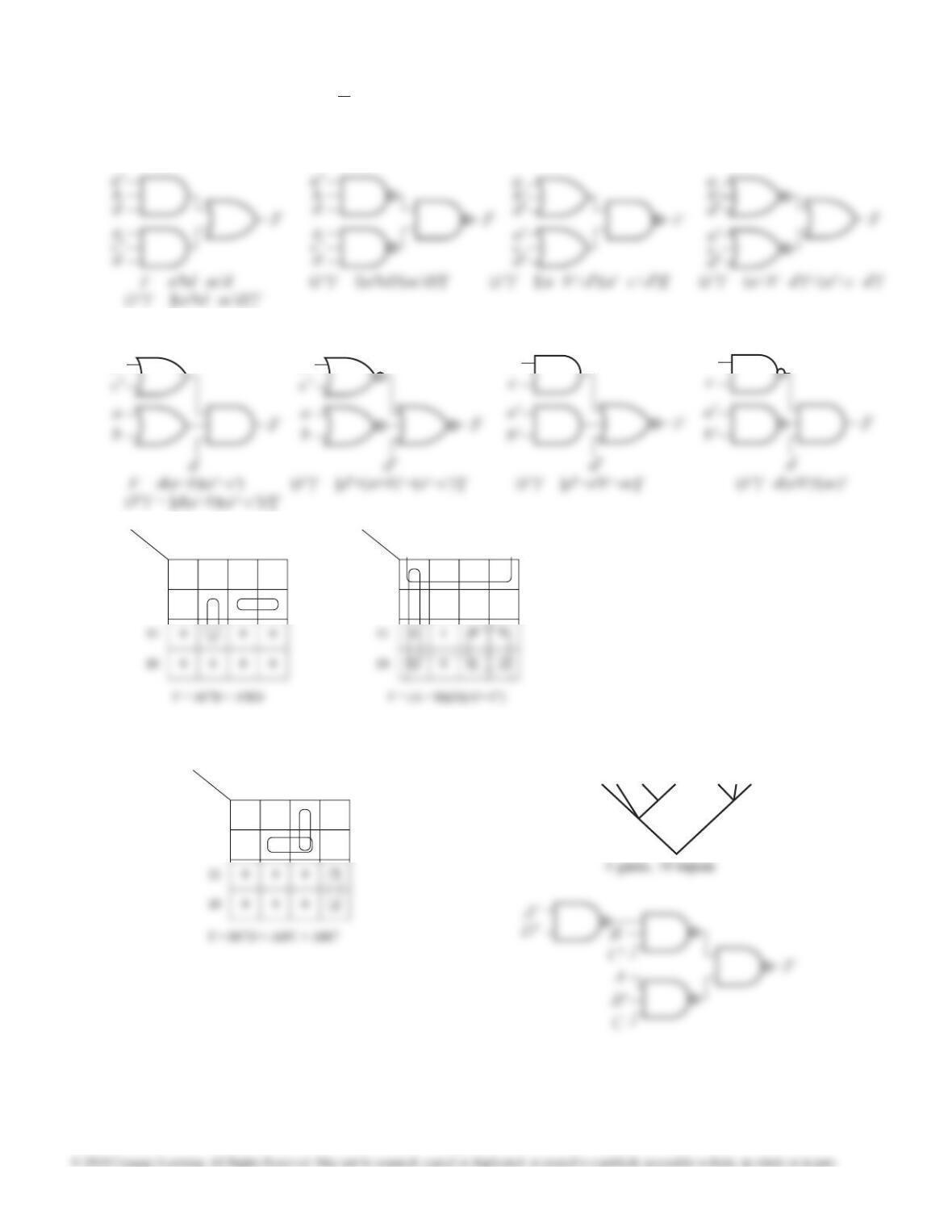
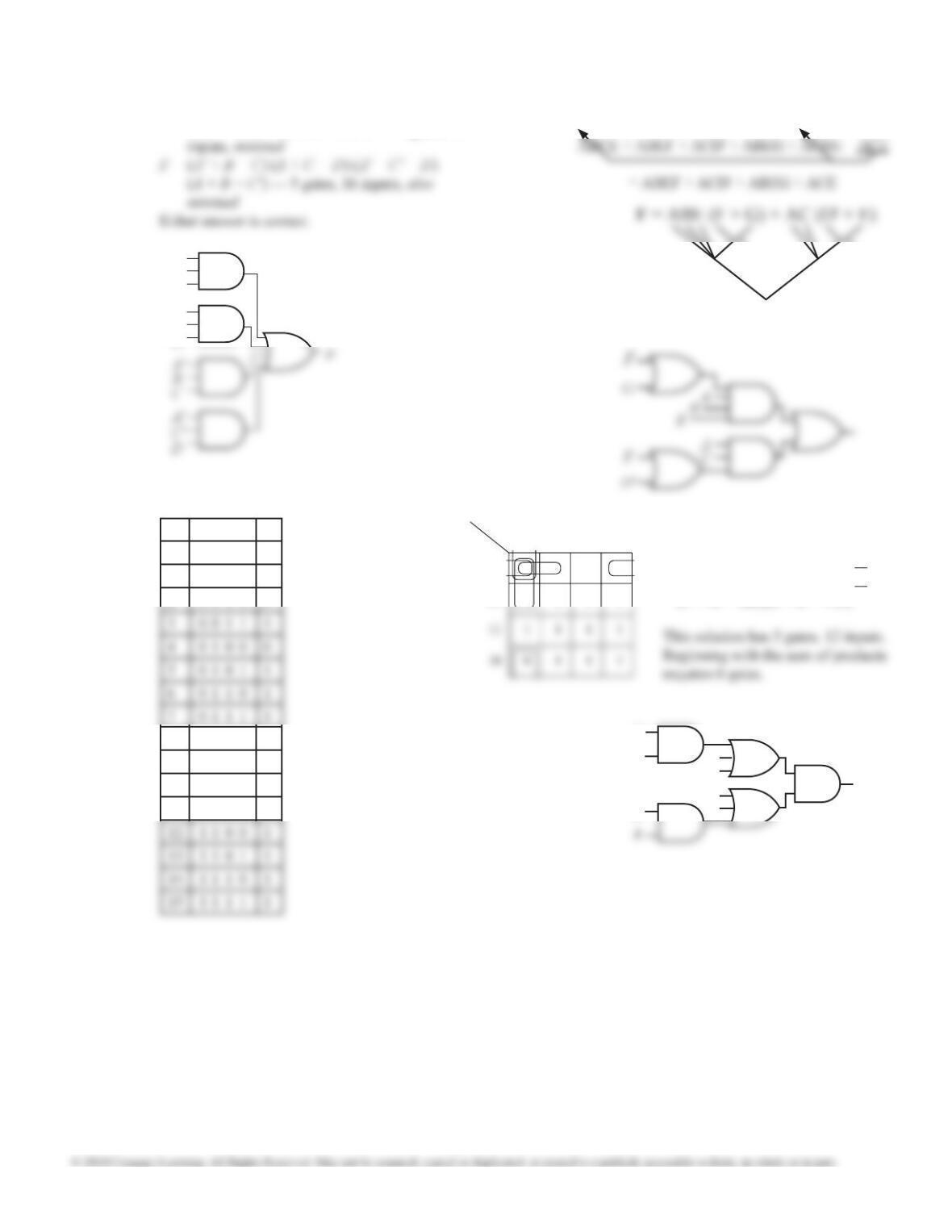
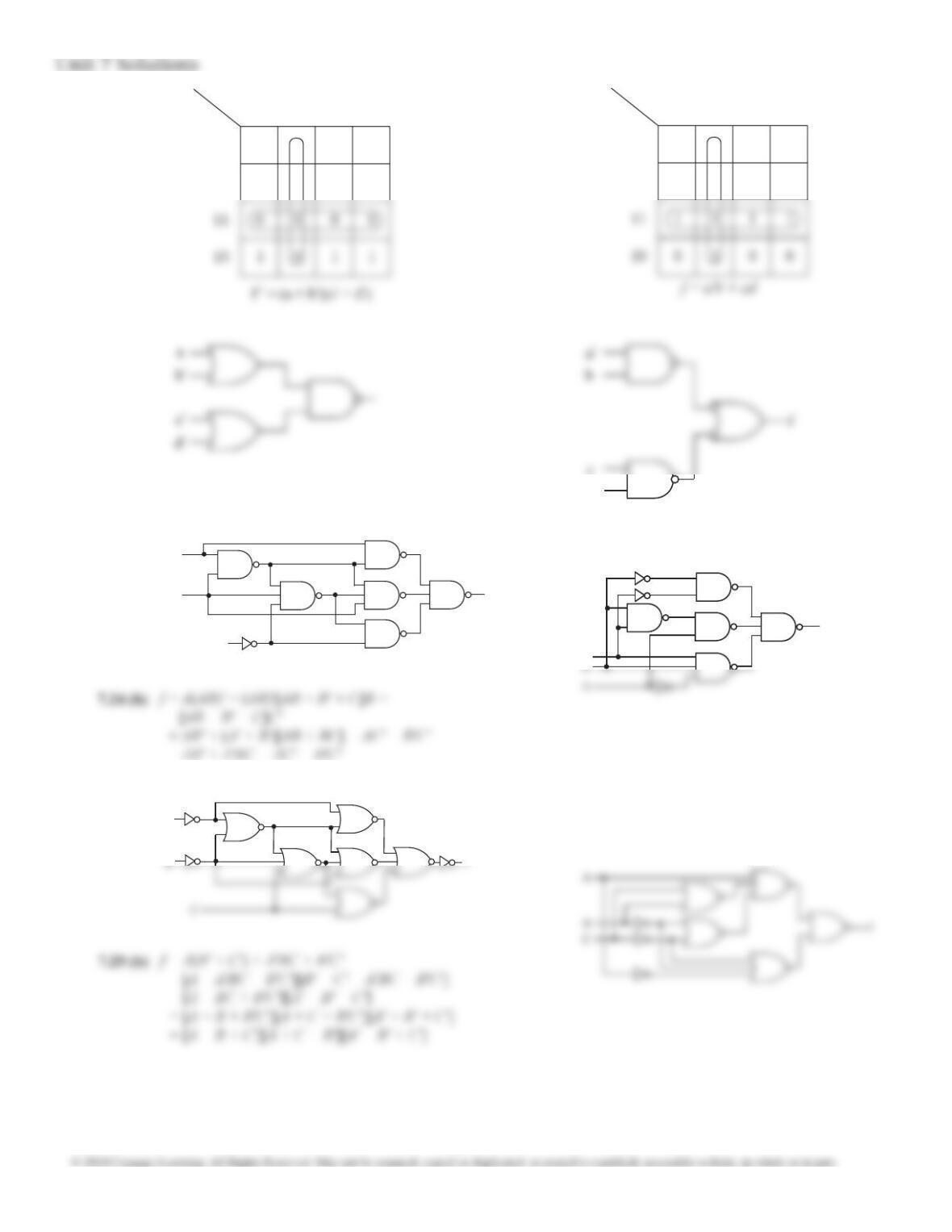
c
d’ a
b
c’
d’ a’
f
f
a b
c d 00 01 11 10
00
01
0
0
1
1
1
1
1
0
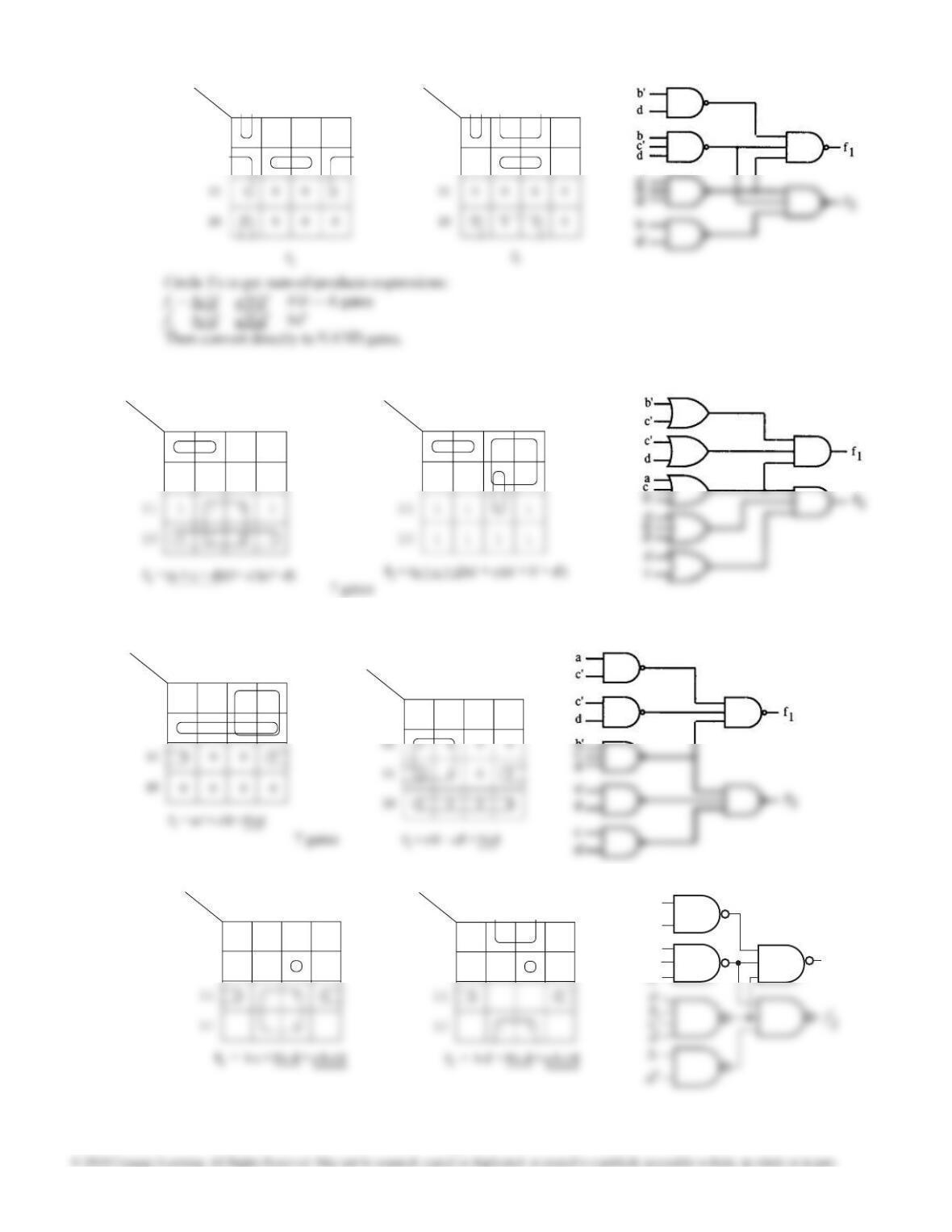
7.15 (a)
From K-maps:
F = a’c + bc’d + ac’d — 4 gates, 11 inputs
F = (a + b + c) (c + d) (a’ + c’) — 4 gates, 10
inputs, minimal
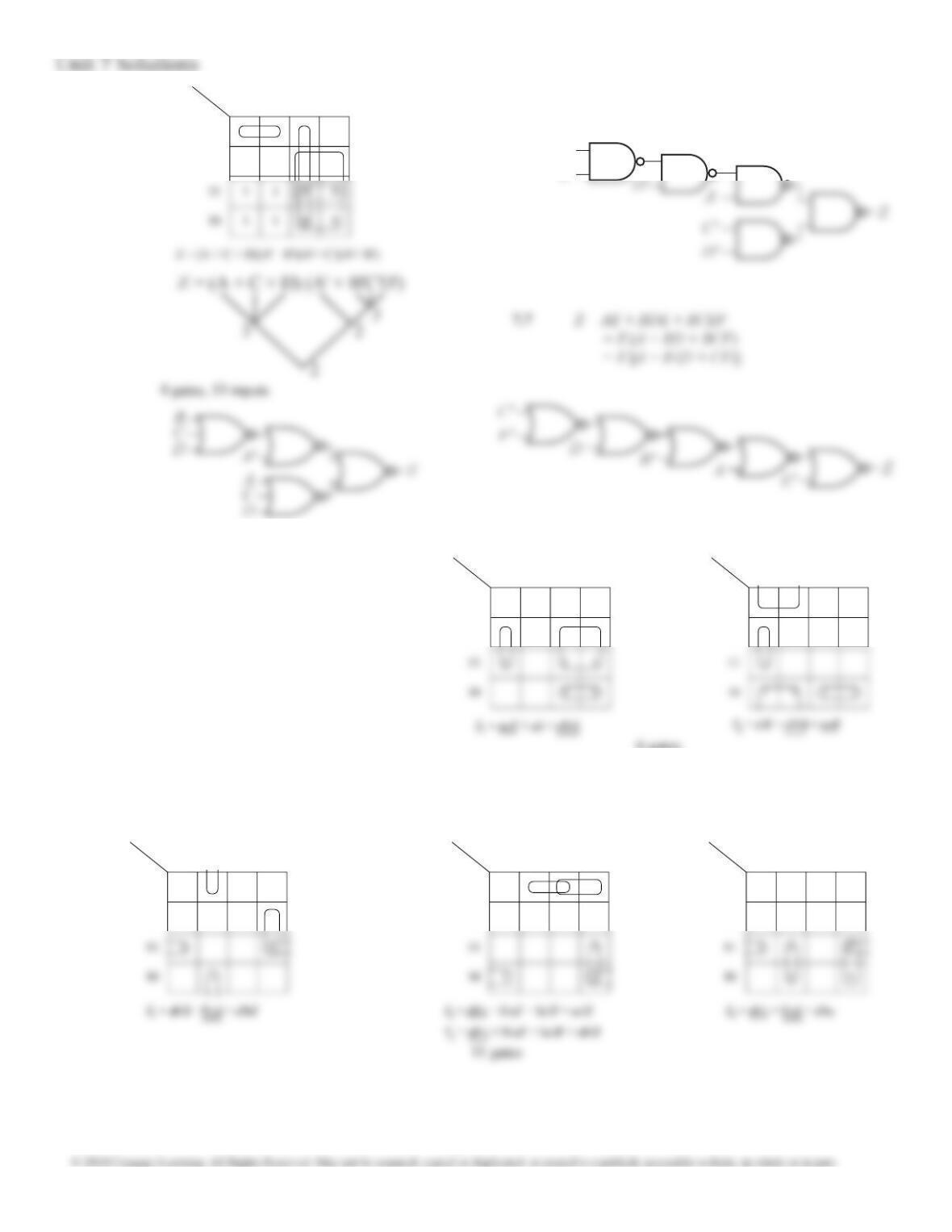
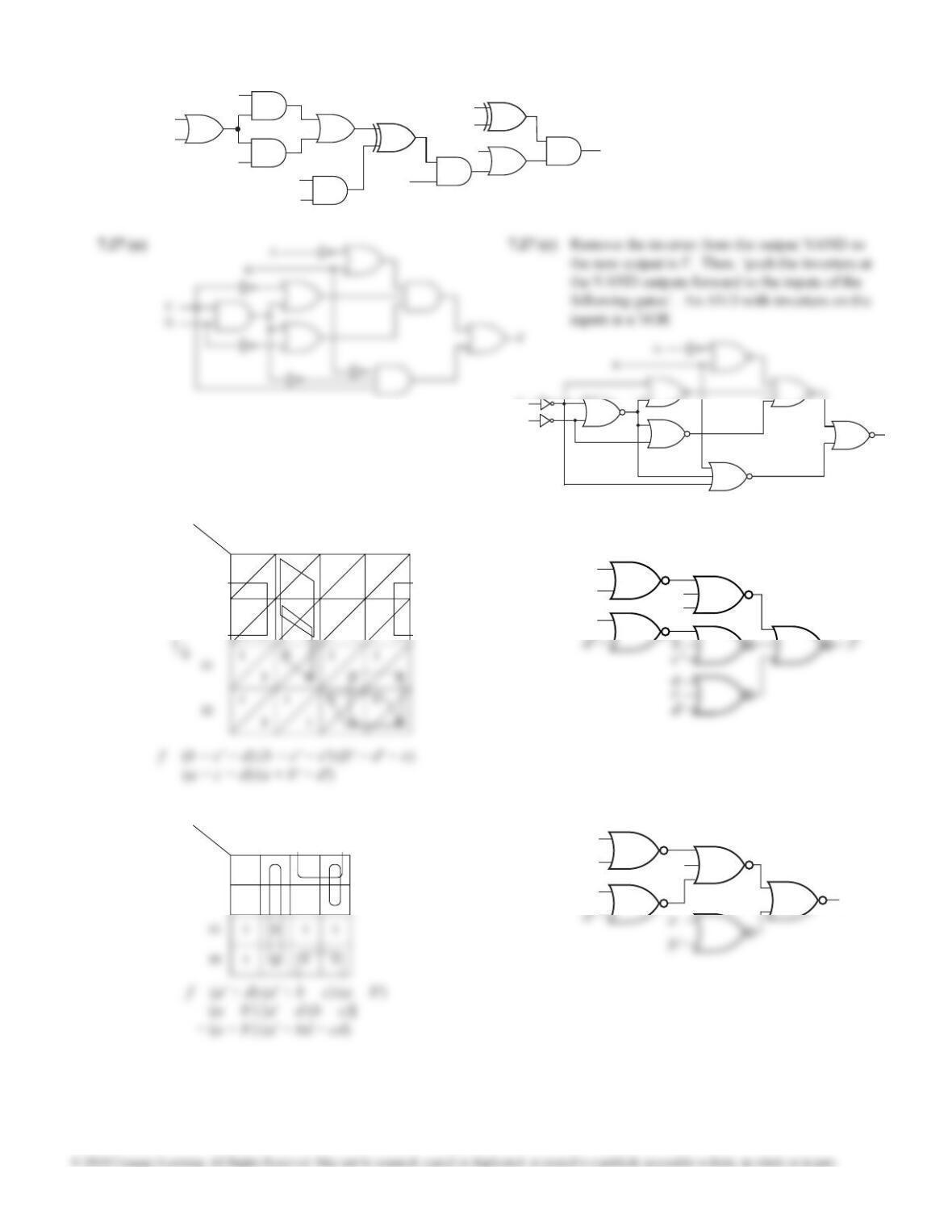
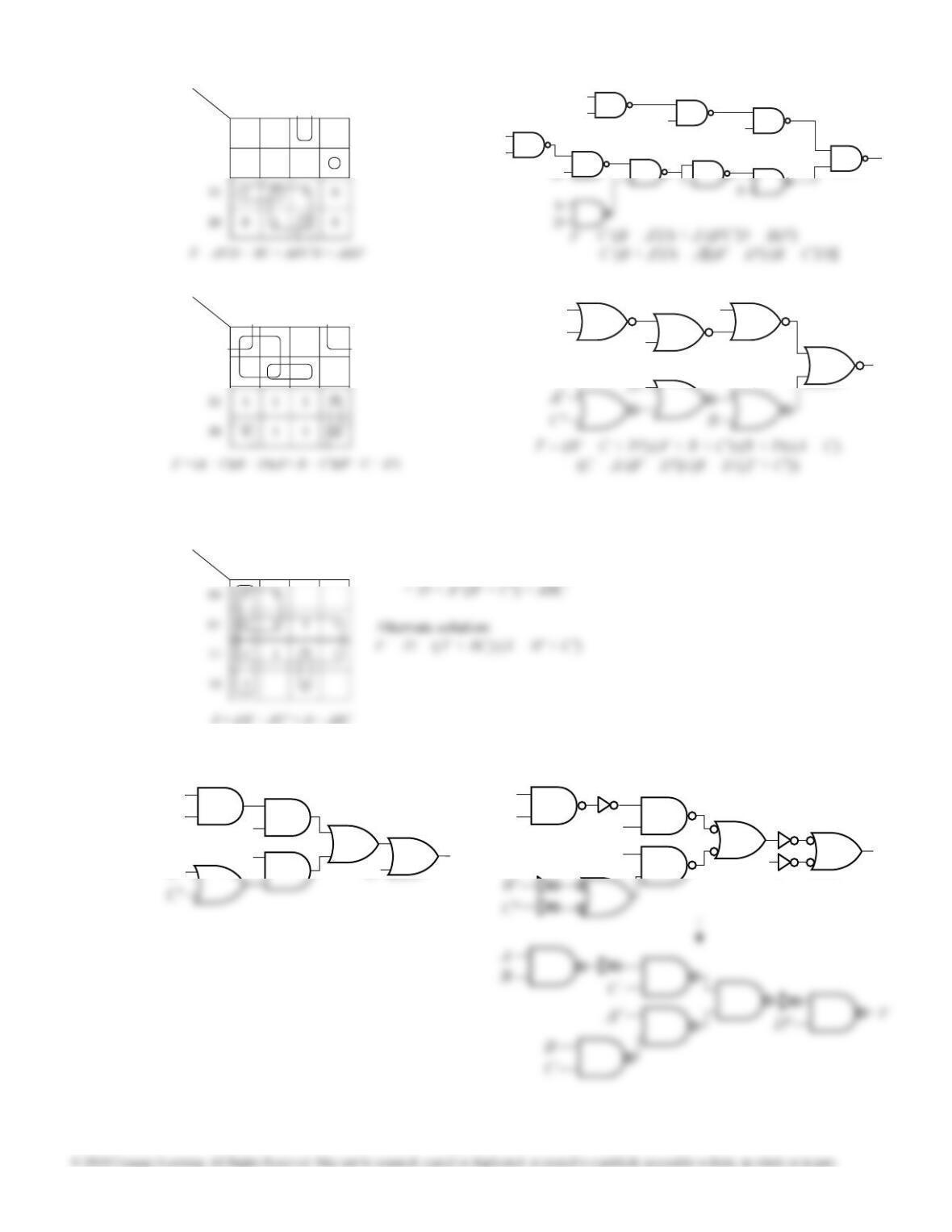
7.15 (b) From K-maps:
F = cd + ac + b’c’ — 4 gates, 9 inputs
F = (b’ + c) (a + c’ + d) — 3 gates, 7 inputs,
minimal
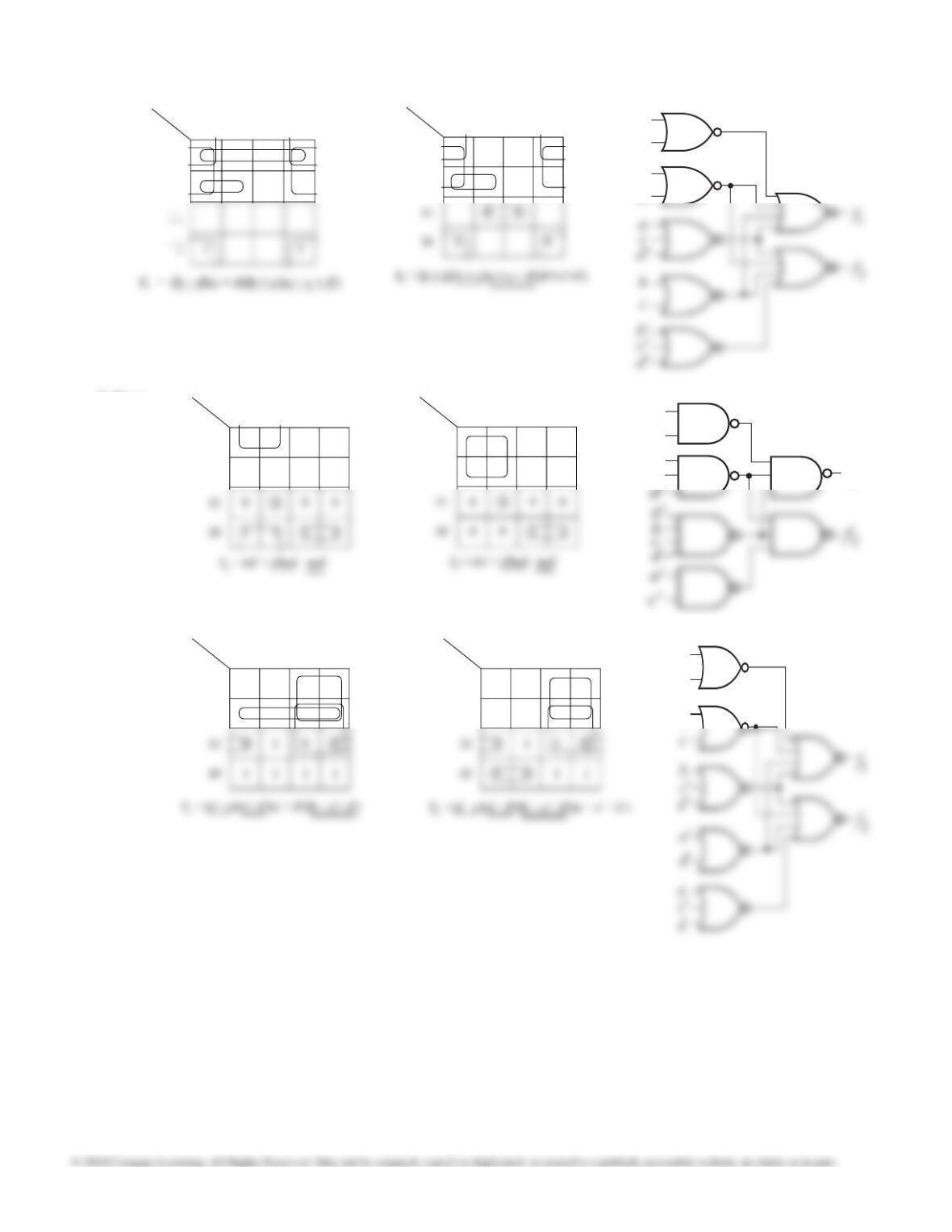
7.15 (c) From K-maps:
F = ad + a’cd’ + bcd
= ad + a’cd’ + a’bc — 4 gates, 11 inputs
7.15 (d) From K-maps:
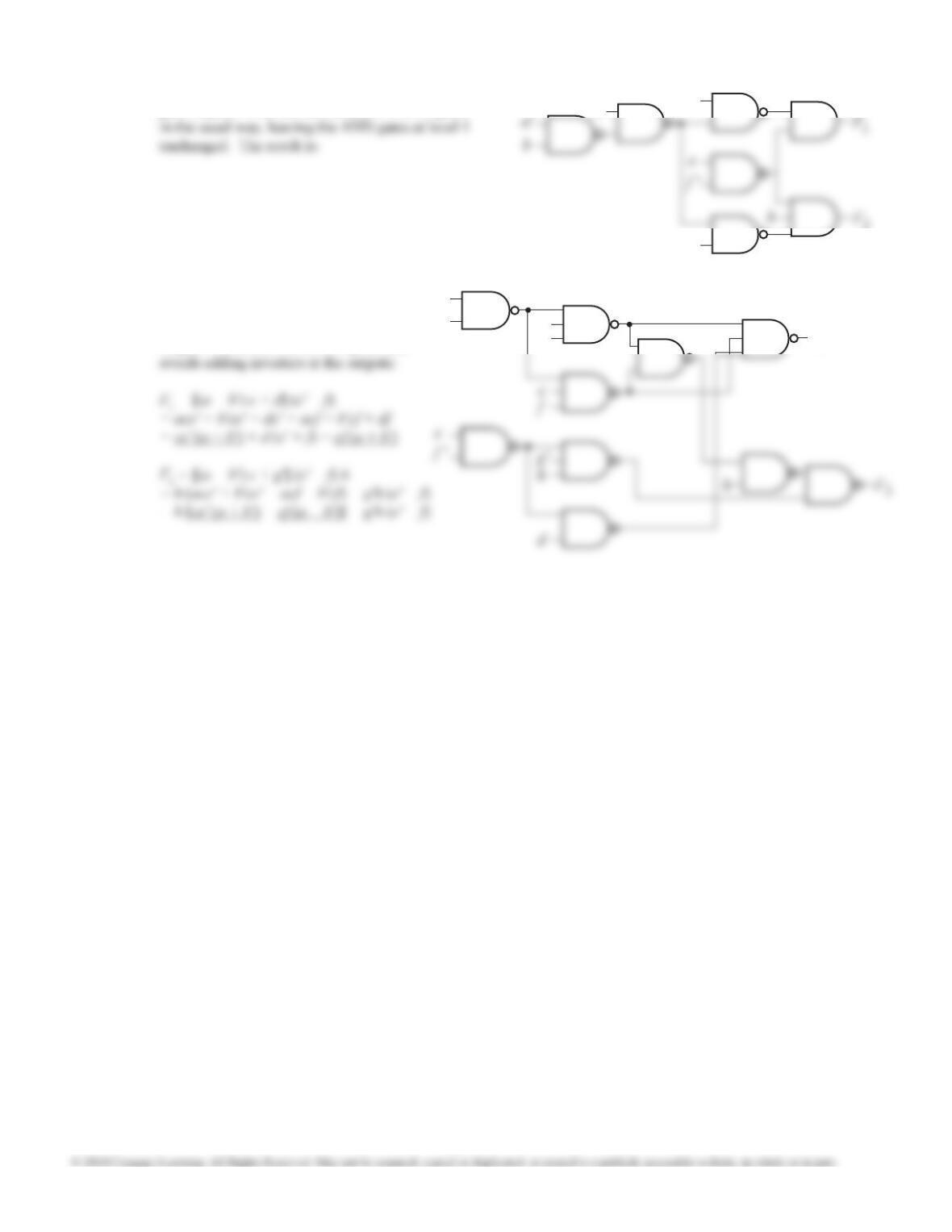
F = a’b + ac + bd’ — 4 gates, 9 inputs, minimal
F = (a + b) (a’ + c + d’) (a’ + b + c)
Unit 7 Solutions
76
A
B
A
C
C’
22
2
4 3
7.16 (a) In this case, multi-level circuits do not improve the
solution. From K-maps:
F = ABC’ + ACD + A’BC + A’C’D — 5 gates, 16
A
B
C’
D
7.16 (b) Too many variables to use a K-map; use algebra.
Add ACE by consensus, then use X + XY = X
5 gates, 13 inputs, minimal
B
C
D
C
B
A
D
F
A B C D F
0 0 0 0 0 0
1 0 0 0 1 0
2 0 0 1 0 0
8 1 0 0 0 0
9 1 0 0 1 1
10 1 0 1 0 1
11 1 0 1 1 1
7.17 (a)
F = ∏ M(0, 1, 2, 4, 8)
A B
C D 00 01 11 10
00
01
0
0
0
1
0
1
1
1
F = (A + C + D) (A + B + C)
(A + B + D) (B + C + D)
= (A + D + BC)(B + C + AD) or
= (A + C + BD)(B + D + AC) or
= (C + D + AB)(A + B + CD)
7.17 (b)
Unit 7 Solutions
77
w’
x’
w’
x’
NAND-NAND
OR-NAND
AND-OR
w
x
NOR-OR
w
x
x’
x’
x
x
AND-NOR
NOR-NOR
NAND-AND
OR-AND
F (w, x, y, z) = (x + y’ + z) (x’ + y + z) w
7.18 (a)
From Karnaugh map: F = wxy + wx’y’ + wz
7.18 (b)
F(a, b, c, d) = ∑ m(4, 5, 8, 9, 13)
From Kmap:
F = a’bc’ + ab’c’ + bc’d
F = a’bc’ + ab’c’ + ac’d
a’
b’
AND-NOR
a
b
NOR-NOR
a’
b’
NAND-AND
a
b
OR-AND
Unit 7 Solutions
7.21 (a) NAND gates:
F = D’ + B’C + A’B
7.21 (b) NAND gates:
f = a’bc’ + ac’d’ + b’cd
7.19 (a)
y
y
x
y z 0 1
00
01
1
1
1
0
From Kmap:
F = (y’ + z) (x’ + y + z’)
x’
y’
y’
f
x’
z
( )
or
x’
y’
y’
f
x’
z
( )
or
x
y z 0 1
00
01
1
1
1
0
7.19 (b)
7.20 (b)
a b
c d 00 01 11 10
00
01
0
0
1
1
0
0
0
0
a b
c d 00 01 11 10
00
01
0
0
1
1
0
0
0
0
Using OR and NOR gates:
7.20 (a)
f f
a
b’
c’
a
b’
c’
c
a’
f
c
b
c
a’
f
c
b
Using NOR gates only:
Unit 7 Solutions
79
7.21 (c) NAND gates:
f = a’b’d’ + bc’d + cd’
7.21 (d) NAND gates:
F = A’B’CD’ + AC’E + C’DE + ADE + A’BCDE’ +
NOR gates:
F = (B’ + D + E) (A’ + C’ + D) (A + B + C’ + D’)
(A + B’ + C + E ) (A’ + B’ + C’ + E)
(A + C + D + E’) (A + B’ + C’ + E’)
7.21 (e) NAND gates:
F=ACD’+ABE’+CDE+A’B’C’D’+B’D’E+A’B’DE’
F=ACD’+ABE’+CDE+A’B’C’E’+A’B’CD+B’D’E
7.21 (g) NAND gates:
f = x’y’ + wy’ + w’z’+ wz
f = x’y’ + wy’ + wx’ + w’z’
7.22 (a) F is 0 if any 3 (or 4) of the inputs are 1 so
F = (A + B’ + C’ + D’) (A’ + B’ + C + D’)
(A’ + B’ + C’ + D’)(A’ + B’ + C’ + D)
7.23 (a)
a b
c d 00 01 11 10
00
01
0
0
1
1
0
0
0
0
b’
c’
b’
d’
80
B
C
A
f
7.24 (a)
C
f
7.24 (c)
7.23 (b) 7.23 (c)
f = A(B’ + C’) + A’BC + B’C’
A
7.25 (a)
7.25 (c)
f = [A + B + C’][A + C + B’][A’ + B’ + C’]
= [A + (B + C’)(B’ + C ][A’ + B’ + C’]
= [A + BC + B’C’][A’ + B’ + C’]
c
d
a b
c d 00 01 11 10
00
01
1
1
0
0
1
1
1
1
a b
c d 00 01 11 10
00
01
0
0
1
1
0
0
0
0
Unit 7 Solutions
81
a’
e’ b’
ed’
7.28 (a) 7.28 (b) f = (b’ + d’ + ae) (b + c’ + de’) (a + c + d)
b c
d e
a
00 01 11 10
00
01
0
0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
C
D
f ‘
f = (A’ + B)(C’ + CD)(D’ + CD) + B’( C’ + D’)C
= (A’ + B)(C’ + D)(D’ + C) + B’CD’
= (A’ + B)(C’D’ + CD) + B’CD’
= A’C’D’ + A’CD + BC’D’ + BCD + B’CD’
7.27 (b)
B
C’
A
D
E
F’
G’
JW
H
I
7.26
b’
d’
c’
a’
f
7.29 a b
c d 00 01 11 10
00
01
1
1
0
0
0
0
0
1
Unit 7 Solutions
82
D
A’
F = B (A’D + C’D) + B’ (A’D’ + CD)
7.33 (c) Alternative:
F = A’ (B’D’ + BD) + D (B’C + BC’)
= D (A’B + BC’) + B’ (A’D’ + CD)
= A’ (B’D’ + CD) + D (B’C + BC’)
=D (A’C + BC’) + B’ (A’D’ + CD)
7.30 (a)
Z= (a’ + b +e + f)(c’ + a’ + b)(d’ + a’ + b)(g+h)
Z = abe’f + c’e’f + d’e’f + gh
7.30 (b)
7.33 (a) A B
C D 00 01 11 10
00
01
1
0
0
1
0
0
0
1
A B
C D 00 01 11 10
00
01
1
1
1
7.31 F = abde’ + a’b’ + c
= (a + b’) (a’ + bde’) + c
7.32
f = x’yz + xvy’w’ + xvy’z’
= x’yz + xvy’ (z’ + w’)
7.33 (b)
Unit 7 Solutions
83
A B
C D 00 01 11 10
00
1
0
0
1
A B
C D 00 01 11 10
00
1
1
7.34 (a)
7.34 (b)
D
B’
C’
A’
7.34 (c) Many solutions exist. Here is one, drawn with alternate gate symbols.
F = A’ (B’C’D’ + B’CD + BCD’) + A (B’C’D + BC’D’ + BCD)
= A’ (B’(C’D’ + CD) + BCD’) + A (B(C’D’ + CD) + B’C’D)
7.35 (a)
A B
C D 00 01 11 10
00
01
0
0
1
1
0
0
0
1
F = A’BC’ + BD + AC + B’CD’
= B (D + A’C’) + C (A + B’D’)
B
C’
A’
D’
Unit 7 Solutions
84
A B
C D 00 01 11 10
00
01
0
0
0
0
0
1
1
0
7.36 A B
C D 00 01 11 10
F = ∑ m(0, 1, 2, 3, 4, 5, 7, 9, 11, 13, 14, 15)
F = D + A’B’ + A’C’ + ABC
7.35 (b)
B’
D’
F
A’
C
A’
D
D
C’
B’
B’
C
F
A B
C D 00 01 11 10
00
01
0
0
0
0
0
1
1
0
A
B
B’
C
A’ D
F
A
B
C
A’ DF
7.36 (a) 7.36 (b)
Unit 7 Solutions
85
A
B
C
A’ DF
7.36 (c)
7.37
D
G
HF’ E
Z = A [BC’ + D + E(F’ + GH)]
7.38
The minimal product-of-sums expression for F is
F = (A + E)(B′ + C′ + E)(A + B + D′)(A + C + D′)
This expression can be multiplied out to give
Unit 7 Solutions
86
7.39 (a)
A
B
The minimal product-of-sums expression for F is
F = (A + B)(A + C)(B + C)(A′ + B′ + C′)
7.39 (b)
A‘
B
F can be multiplied out as follows:
F = (A + B)(A + C)(B + C)(A′ + B′ + C′)
= (A + B)(B + C)(A + B′ + C)(A′ + B′ + C′)
= (AC + B)[B′ + (A + C)(A′ + C′)]
7.39 (c)
A
C‘
B
The minimal sum-of-products expression for F is
F = ABC′ + AB′C + A′BC
7.39 (d)
BA
F
C
One factorization of F is
F = A(BC′ + B′C) + C(A′B + AB′)
7.40 (a)
C
A
B
An inverter on the output of an XOR can be moved
to one of its inputs.
7.40 (b)
F = (A ⊕ BC) + (A′ ⊕ B′C′) = A′BC + AB′ + AC′
+ AB′C′ + A′B + A′C
= AB′ + AC′ + A′B + A′C
= A(B′ + C′) + A′(B + C)
= (A + B + C)(A′ + B′ + C′)
7.40 (c)
A
B
F = A(B′ + C′) + A′(B + C)7.41 (a) No—NOR-AND is equivalent to NOT-AND-
AND.
(b) Yes—NOR-OR is equivalent to OR-AND-NOT.
(c) No—NOR-NAND is equivalent to OR-OR.
(d) Yes—NOR-XOR is equivalent to NOT-AND-
Unit 7 Solutions
87
7.42
8 gates
f
1
a b
c d 00 01 11 10
00
01
X X
1
f
2
a b
c d 00 01 11 10
00
01
1
X
1 1
1
X
f
3
a b
c d 00 01 11 10
00
01
1
X X
X
1
7.43 a b
c d 00 01 11 10
00
01
1
1
a b
c d 00 01 11 10
00
01
1
1
1
1
6 gates
7.44 x
y z 0 1
00
01
1
1
x
y z 0 1
00
01
1
1
x
y z 0 1
00
01
1
1
1
7.45 (a) a b
c d 00 01 11 10
00
01
1
1
0
1
0
1
0
1
a b
c d 00 01 11 10
00
01
1
0
1
1
0
0
1
1
Unit 7 Solutions
88
7.46 (a)
a b
c d 00 01 11 10
00
01
0
1
0
1
1
1
1
1
a b
c d 00 01 11 10
00
01
0
1
0
1
0
0
0
0
Circle 0’s
a b
c d 00 01 11 10
00
01
0
1
0
1
1
1
1
1
f2
a b
c d 00 01 11 10
00
0
0
0
0
Circle 1’s to get sum-of-products expressions:
Then convert directly to NAND gates
7.46 (b)
b
c
b’
c
f
1
a b
c d 00 01 11 10
00
01
1
a b
c d 00 01 11 10
00
01
1
1
1
7.47 (a)
7.45 (b) a b
c d 00 01 11 10
00
01
1
1
0
1
0
1
0
1
a b
c d 00 01 11 10
00
01
1
0
1
1
0
0
1
1
Unit 7 Solutions
89
b
c
d
d
a b
c d 00 01 11 10
00
01
0
0
0
0
0
0
0
a b
c d 00 01 11 10
00
01
0
0
0
0
0
7.47 (b)
7.48 (a)
a’
d’
a
c
f
1
a’
c
d’
a b
c d 00 01 11 10
00
01
1
0
1
0
0
0
0
0
a b
c d 00 01 11 10
00
01
1
1
1
1
0
0
0
0
a b
c d 00 01 11 10
00
01
1
0
1
0
0
0
0
0
a b
c d 00 01 11 10
00
01
1
1
1
1
0
0
0
0
7.48 (b)
Unit 7 Solutions
90
7.49 (a)
cd’
g
a’
b
e’
c
F1
The circuit consisting of levels 2, 3, and 4 has OR
gate outputs. Convert this circuit to NAND gates
7.49 (b) One solution would be to replace the
two AND gates in (a) with NAND
gates, and then add inverters at the
output. However, the following solution