Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
57
Unit 6 Solutions
Unit 6 Problem Solutions
100011, 5 0-01 a'c'd
501011, 9 -001 b'c'd
910015, 7 01-1 a'bd
12 11009, 11 10-1 ab'd
6.2 (a)
000000, 1 000- a'b'c' 1, 3, 5, 7 0--1 a'd
100010, 8 -000 b'c'd' 1, 5, 3, 7 0--1
810001, 3 00-16, 7, 14, 15 -11- bc
300111, 5 0-016, 14, 7, 15 -11-
6.2 (b)
1 5 7 911 12 14 15
1, 5 a'c'd × ×
1, 9 b'c'd × ×
5, 7 a'bd × ×
6.3 (a)
0 1 3 5 6 7 8 10 14 15
1, 3, 5, 7 a'd × × × ×
6, 7, 14, 15 bc × × × ×
f = abd' + a'c'd + ab'd + bcd
f = abd' + b'c'd + a'bd + acd
6.3 (b)
f = a'd + bc + a'b'c' + ab'd'
f = a'd + bc + b'c'd' + ab'd'
Unit 6 Solutions
100011, 3 00-11, 3, 5, 7 0--1 a'd
200101, 5 0-011, 5, 3, 7 0--1
401001, 9 -0011, 5, 9, 13 --01 c'd
300112, 3 001-1, 9, 5, 13 --01
501012, 6 0-102, 3, 6, 7 0-1- a'c
601102, 10 -010 b'cd' 2, 6, 3, 7 0-1-
910014, 5 010-4, 5, 6, 7 01-- a'b
13, 15 11-1
6.4
6.5 100011, 5 0-011, 5, 9, 13 --01 C'D
401001, 9 -0011, 9, 5, 13 --01
810004, 5 010-4, 5, 12, 13 -10- BC'
501014, 12 -1004, 12, 5, 13 -10-
910018, 9 100-5, 7, 13, 15 -1-1 BD
Prime implicants: C'D, BC', BD, AC', AD, AB
1 3 4 5 6 7 10 12 13
1, 3, 5, 7 a'd × × × ×
1, 5, 9, 13 c'd × × ×
9 12 13 15
P1 (1, 5, 9, 13) C'D × ×
P2 (4, 5, 12, 13) BC' × ×
59
Unit 6 Solutions
6.5
(cont.)
6.6 (a) A B
C D 00 01 11 10
00
01
1
E
1
1
1
A B
C D 00 01 11 10
00
01
1 1
1
1
A B
C D 00 01 11 10
00
01
1
X
G
E
X
F
1
A B
C D 00 01 11 10
00
01
X
1
X
X
X
E = 0 E = 1
6.6 (b) A B
C D 00 01 11 10
00
01
1
X
X1
A B
C D 00 01 11 10
00
01
X
X
1
XX
E = F = G = 0 E = 1; F = G = 0
(P1 + P4 + P5) (P2 + P4 + P6) (P1 + P2 + P3 + P4 + P5 + P6) (P3 + P5 + P6)
= (P4 + P1P2 + P1P6 + P2P5 + P5P6) (P3 + P5 + P6)
A B
C D 00 01 11 10
00
01
X
X
X
1
X
A B
C D 00 01 11 10
00
01
X
X
1
XX
Z = A'B' + ABD + E (B'C' + A'C) +
F (AB) + G (A'D)
F = 1; E = G = 0 G = 1; E = F = 0
000000, 4 0-00 a'c'd'
401004, 5 010- a'bc'
300113, 7 0-11 a'cd
501013, 11 -011 b'cd
6.7 (a)
60
Unit 6 Solutions
0 3 4 5 7 911 13
0, 4 a'c'd' × ×
4, 5 a'bc' × ×
3, 7 a'cd × ×
6.8 (a)
2 4 5 6 9 10 11 12 13 15
2, 6 a'cd' × ×
2, 10 b'cd' × ×
6.8 (b)
f = bc' + ad + a'cd' + b'cd'
f = bc' + ad + a'cd' + ab'c
200102, 6 0-10 a'cd' 4, 5, 12, 13 -10- bc'
401002, 10 -010 b'cd' 4, 12, 5, 13 -10-
501014, 5 010-9, 11, 13, 15 1--1 ad
601104, 6 01-0 a'bd' 9, 13, 11, 15 1--1
6.7 (b)
f = b'c + bc'd' + cd + b'd + ab
f = b'c + bc'd' + cd + ad + ab
2 3 4 7 911 12 13 14
4, 12 bc'd' × ×
1, 3, 9, 11 b'd × × ×
2, 3, 10, 11 b'c × × ×
100011, 3 00-11, 3, 9, 11 -0-1 b'd
200101, 9 -0011, 9, 3, 11 -0-1
401002, 3 001-2, 3, 10, 11 -01- b'c
300112, 10 -0102, 10, 3, 11 -01-
910014, 12 -100 bc'd' 3, 7, 11, 15 --11 cd
6.9 (a)
Unit 6 Solutions
000000, 1 000-0, 1, 8, 9 -00- b'c'
100010, 8 -0000, 8, 1, 9 -00-
810001, 5 0-011, 5, 9, 13 --01 c'd
501011, 9 -0011, 9, 5, 13 --01
601108, 9 100-8, 9, 10, 11 10-- ab'
6.9 (b)
f = a'bc + b'c' + ab' + c'd
0 1 5 6 8 911 13
5, 7 a'bd ×
6, 7 a'bc ×
0, 1, 8, 9 b'c' × × × ×
0000000, 2 000-00, 2, 4, 6 00--00, 2, 4, 6, 8, 10, 12, 14 0---0 A'E'
2000100, 4 00-000, 2, 8, 10 0-0-00, 2, 8, 10, 4, 6, 12, 14 0---0
4001000, 8 0-0000, 2, 16, 18 -00-0 B'C'E' 0, 4, 8, 12, 2, 6, 10, 14 0---0
8010000, 16 -00000, 4, 2, 6 00--0
6.11
6.9 (c) f = a'b + bc + ab'c' + bd + cd
f = a'b + bc + ab'c' + ad + cd
f = a'b + bc + ab'c' + ad + a'c
6.10 Prime implicants: abc', bc'd, a'bd, b'cd, a'c, a'b'd'
f = abc' + b'cd + a'c + a'b'd' + a'bd
f = abc' + b'cd + a'c + a'b'd' + bc'd
62
Unit 6 Solutions
0 2 6 7 8 10 11 12 13 14 16 18 19 29 30
6, 7 A'B'CD × ×
18, 19 AB'C'D × ×
13, 29 BCD'E × ×
14, 30 BCDE' × ×
6.11
cont.
6.12 (a)
0 00000 0, 1 0000- 0, 1, 2, 3 000-- 0, 1, 2, 3, 8, 9, 10, 11 0-0--*
1 00001 0, 2 000-0 0, 1, 8, 9 0-00-
2 00010 0, 4 00-00* 0, 2, 8, 10 0-0-0
4 00100 0, 8 0-000 1, 3, 9, 11 0-0-1
8 01000 1, 3 000-1 2, 3, 10, 11 0-01-
3 00011 1, 9 0-001 8, 9, 10, 11 010--
9 01001 2, 3 0001- 3, 11, 19, 27 --011*
Prime Implicants: A'B'D'E', AB'DE, AB'CE,
ACD'E, AB'CD, ACDE', ABCD'. ABCE',
C'DE, A'C'
63
Unit 6 Solutions
6.12 (b)
0 00000 0, 1 0000-* 11, 15, 27, 31 -1-11*
1 00001 0, 2 000-0* 14, 15, 30, 31 -111-*
2 00010 0, 4 00-00* 26, 27, 30, 31 11-1-*
4 00100 0, 8 0-000*
8 01000 1, 17 -0001*
17 10001 2, 18 -0010*
Prime Implicants: A'B'D'E', AB'DE, AB'CE,
ACD'E, AB'CD, ACDE', ABCD'. ABCE',
C'DE, A'C'
(0, 1)
0124811
A'B'C'D'
XX
13
14 17 18 20 21
26 27 30 31
15
Q
Essential prime implicants: A'C'D'E', BDE, A'BCE, BCD
Petrick’s Method for remaining minterms: (Q+T)(R+U)(S+V)(T+W)(U+X)(V+Y)(W+Y)(X+Z)
f = BCD + A'BCE + BDE + A'C'D'E' + ABD + B'C'DE' + AB'CD' + B'C'D'E + A'B'D'E'
f = BCD + A'BCE + BDE + A'C'D'E' + ABD + B'C'D E' + AB'D'E + B'CD'E' + A'B'C'D'
6.12 (b)
(cont.)
6.13 (a)
16 10000 16, 17 1000- 16, 17, 24, 25 1-00-*
5 00101 16, 18 100-0 16, 18, 24, 26 1-0-0*
6 00110 16, 20 10-00* 5, 7, 13, 15 0-1-1*
12 01100 16, 24 1-000 6, 7 14, 15 0-11-*
17 10001 5, 7 001-0 12, 13, 14, 15 011--*
18 10010 5, 13 0-101
20 10100 6, 7 0011-
Prime implicants of f ': AB'D'E', BCDE, AC'D',
AC'E', A'CE, A'CD, A'BC
64
Unit 6 Solutions
6.14 (a)
1 0001 1, 3 00-1* 1, 5, 9, 13 --01*
4 0100 1, 5 0-01 4, 5, 12, 13 -10-*
8 1000 1, 9 -001 4, 6, 12, 14 -1-0*
3 0011 4, 5 010- 8, 9, 12, 13 1-0-*
5 0101 4, 6 01-0 8, 10, 12, 14 1--0*
6 0110 4, 12 -100 12, 13, 14, 15 11--*
(1, 3)
(1, 5, 9, 13)
135689
A'B'D
XX
12
14
X
X
X
15
C'D
Prime implicants: A'B'D, A B, A C', C'D, A D',
B D', B C'
6.14 (b)
0 0000 0, 2 00-0*
2 0010 0, 4 0-00*
4 0100 2, 10 -010*
(7)
(13)
0 2 7 11 8 9
A'BCD
X
12
14
15
ABC'D
6.13 (b)
16 10000 16, 24 1-000* 3, 7, 19, 23 -0-11*
3 00011 3, 7 00-11 6, 7, 22, 23 -011-*
5 00101 3, 19 -0011 24, 25, 28, 29 11-0-*
6 00110 5, 7 001-1*
9 01001 6, 7 0011-
10 01010* 6, 22 -0110
Prime implicants of f ': A'BC'DE', AC'D'E', A'B'CE,
BC'D'E, BCD'E', B'DE, B'CD, ABD'
3567910
12
16 19 22 23 24
25 28 29
(10) A'BC'DE'
Unit 6 Solutions
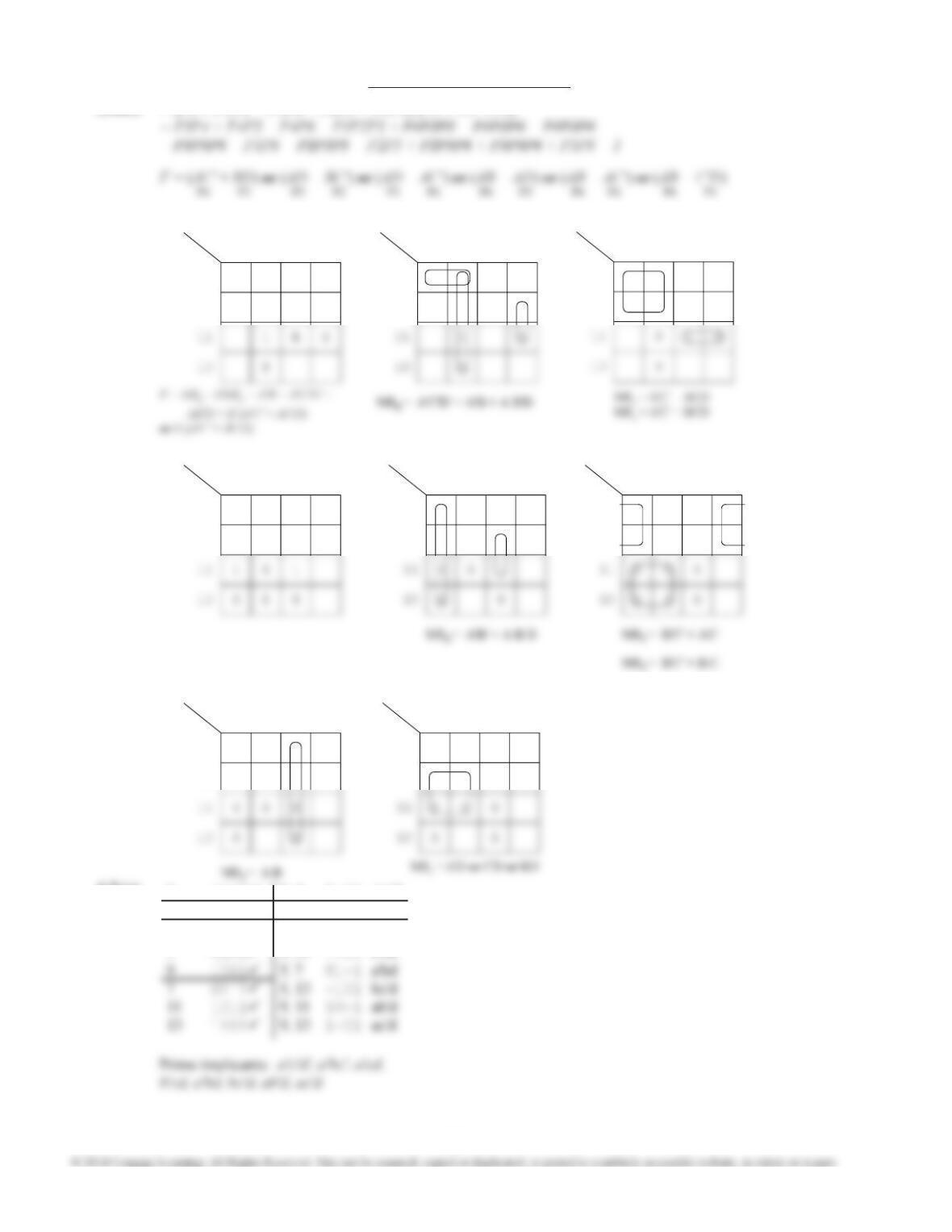
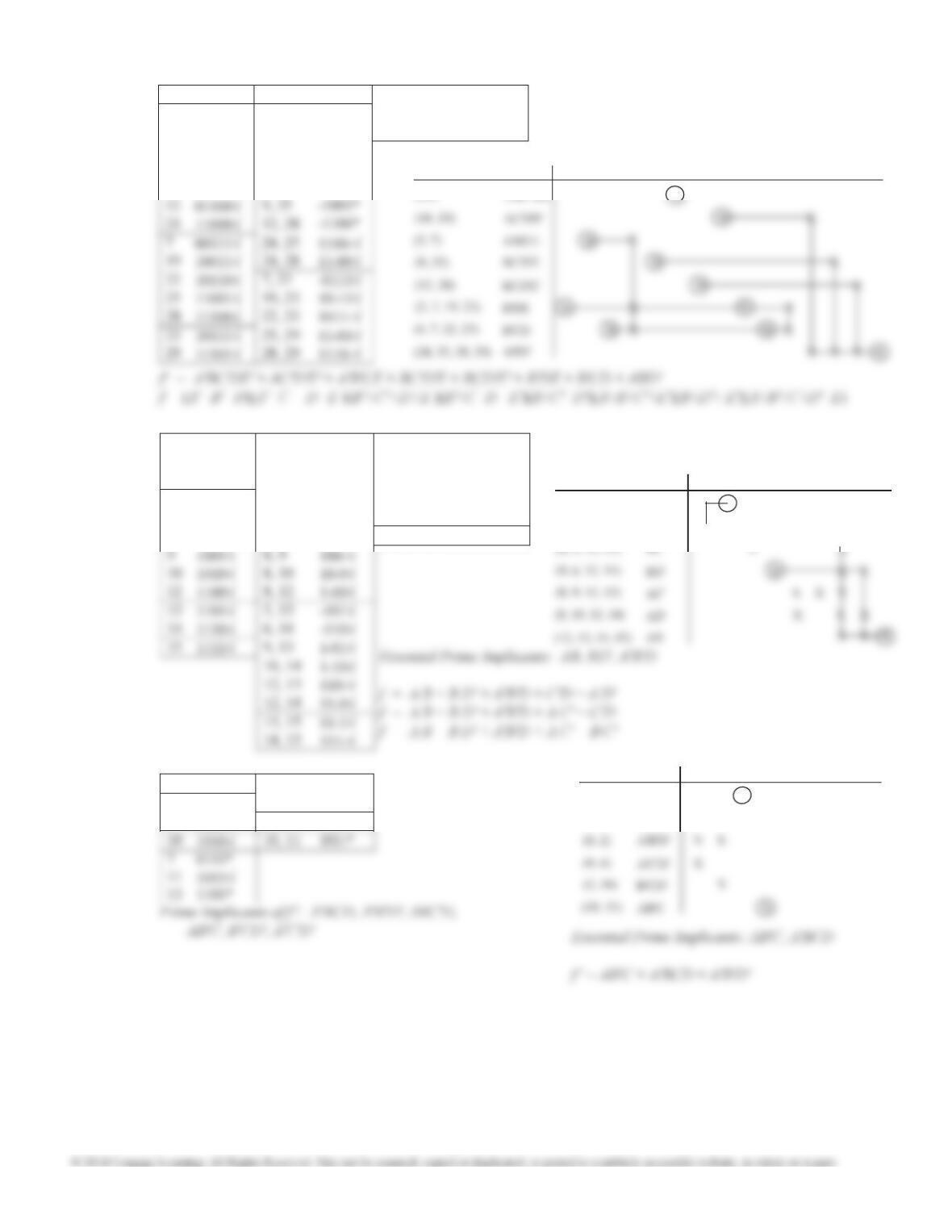
6.15 (a)
1 00001 1, 5 00-01 1, 5, 9, 13 0--01*
2 00010 1, 9 0-001 1, 9, 17, 25 --001*
4 00100 1, 17 -0001 4, 5, 6, 7 001--*
5 00101 2, 6 00-10* 4, 5, 12, 13 0-10-*
6 00110 4, 5 0010- 4, 6, 20, 22 -01-0*
9 01001 4, 6 001-0 4, 12, 20, 28 --100*
12 01100 4, 12 0-100 5, 7, 13, 15 0-1-1*
17 10001 4, 20 -0100 20, 22, 28, 30 1-1-0*
Prime Implicants: a c e', a'c e, c d'e', a'c d', a'b'c,
b'c e', a'b'd e', c'd'e, a'd'e
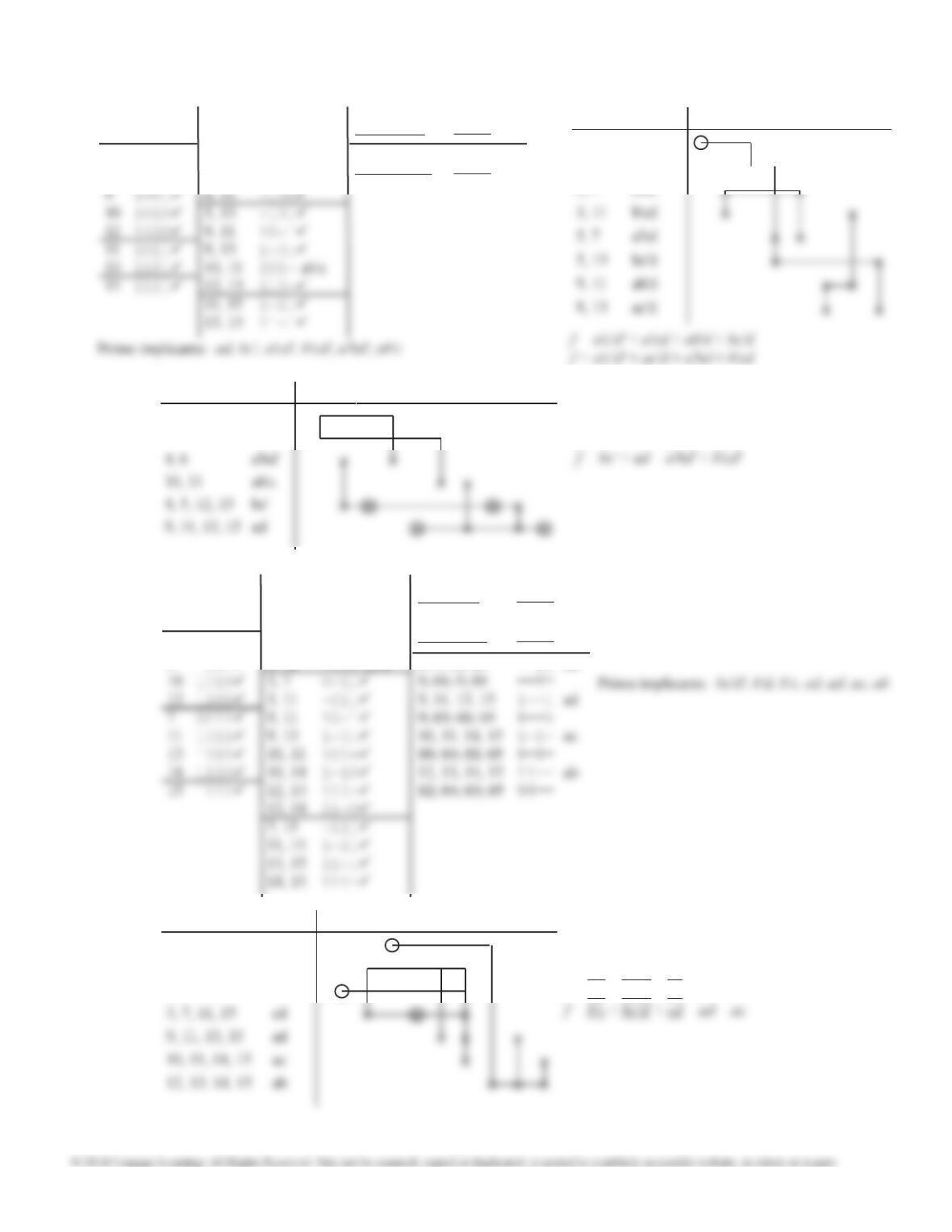
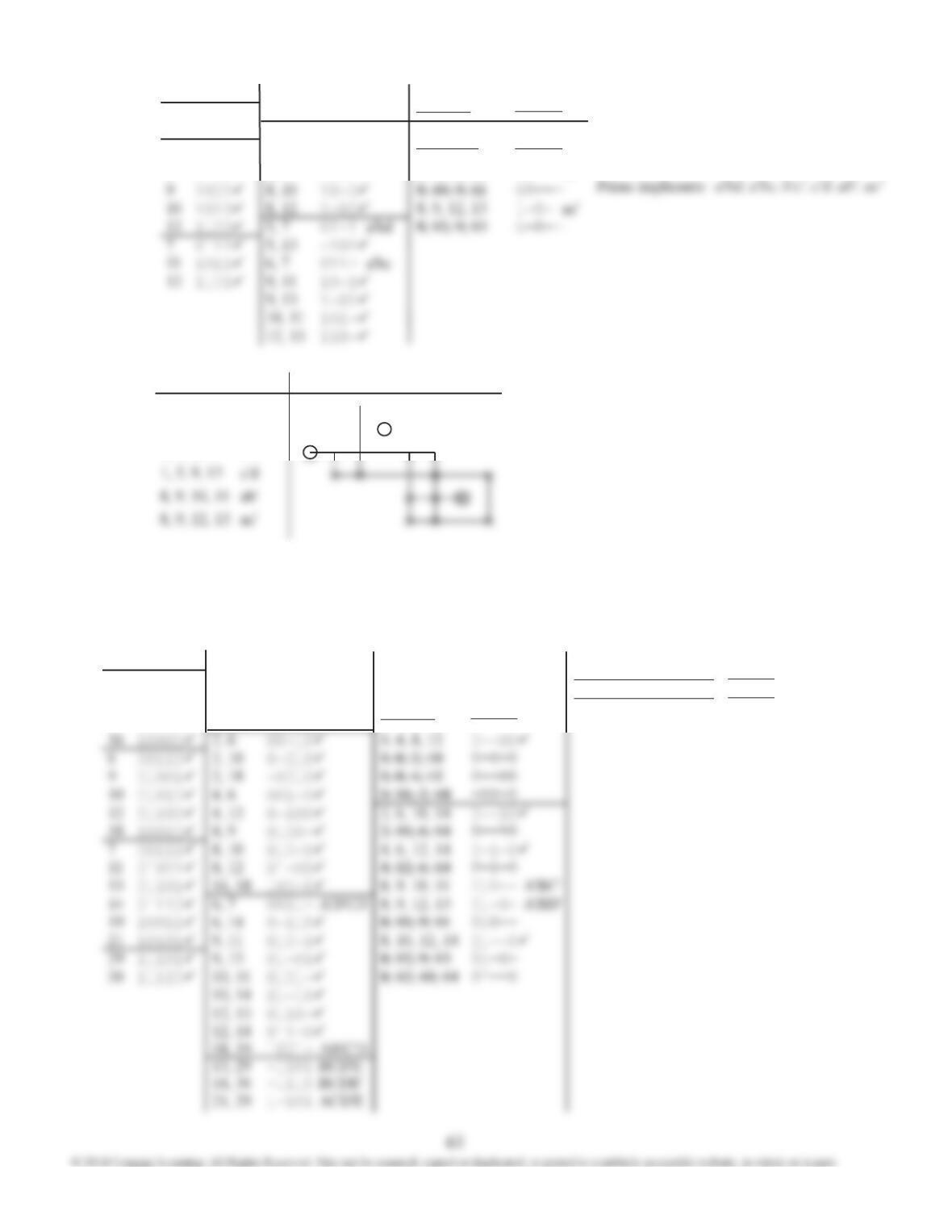
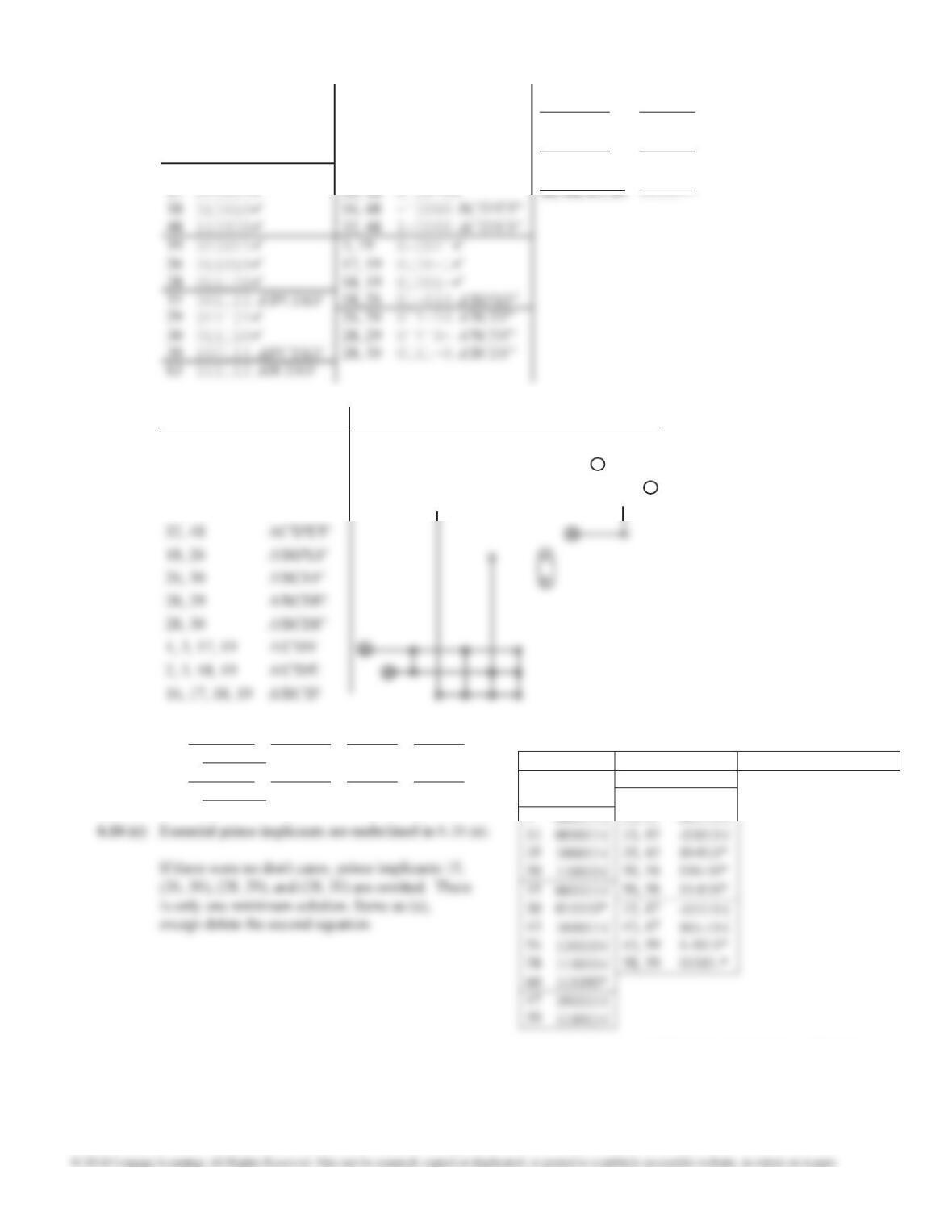
6.15 (b)
0 00000 0, 8 0-000 0, 8, 16, 24 --000*
8 01000 0,16 -0000 8, 10, 24, 26 -10-0*
16 10000 8, 10 010-0 16, 18, 24, 26 1-0-0*
3 00011 8, 24 -1000 3, 11, 19, 27 --011*
10 01010 16, 18 100-0 10, 11, 26, 27 -101-*
18 10010 16, 24 1-000 18, 19, 26, 27 1-01-*
24 11000 3, 11 0-011 19, 23, 27, 31 1--11*
11 01011 3, 19 -0011 21, 23, 29, 31 1-1-1*
14 01110 10, 11 0101-
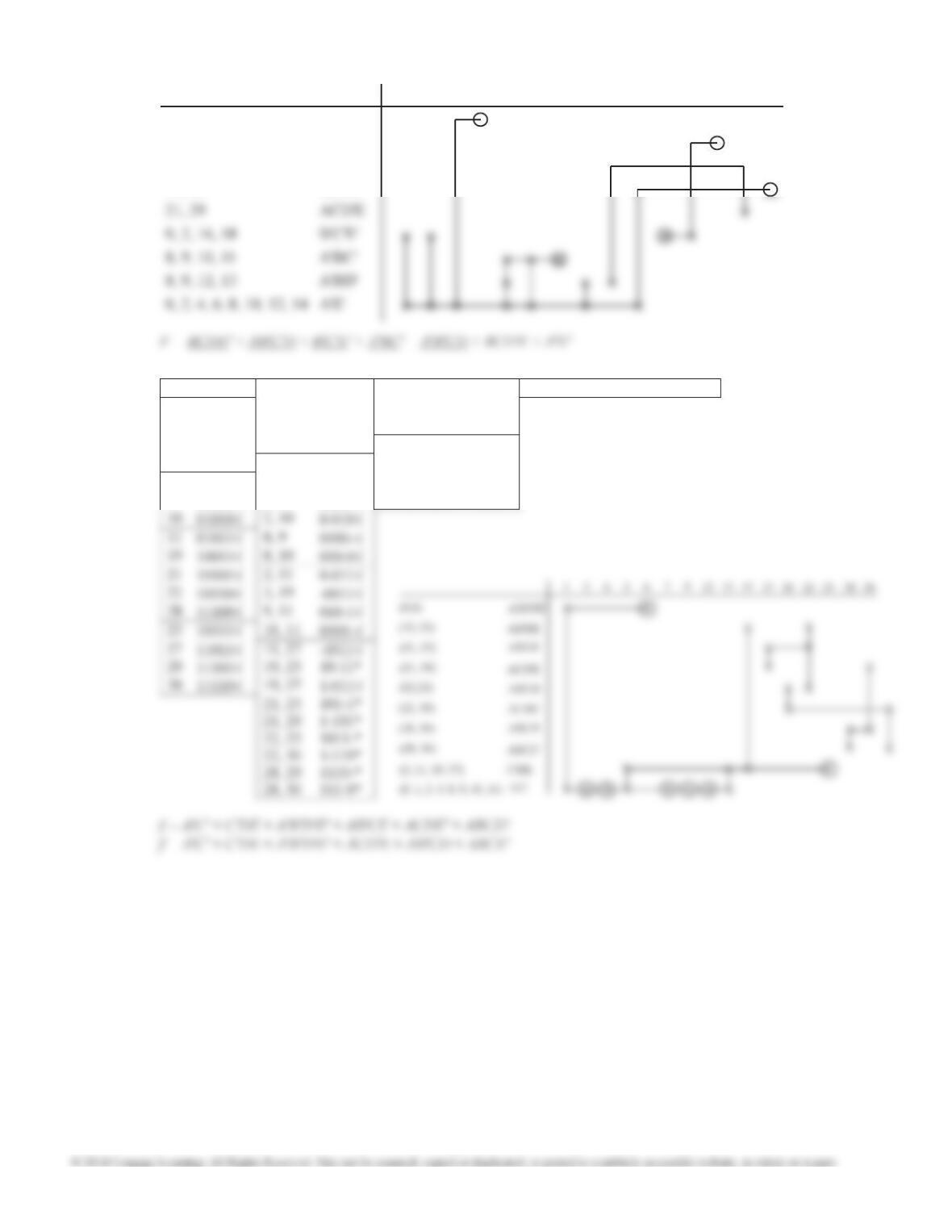
Prime Implicants of f ': ace, ade, ac'd, ac'e', bc'd,
a'bde', bc'e', c'de, c'd'e'
0 3 8 31
10 11
14
16 18 19 21 23
24 26 27 29
66
Unit 6 Solutions
1 2 3 16 17 18 19 26 32 39 48 63
15 A'B'CDEF
39 AB'C'DEF ×
63 ABCDEF ×
16, 48 BC'D'E'F' × ×
G = AB'C'DEF + ABCDEF + A'C'D'F + A'C'D'E
+ AC'D'E'F' + A'BC'D' + A'BD'EF'
G = AB'C'DEF + ABCDEF + A'C'D'F + A'C'D'E
+ AC'D'E'F' + A'BC'D' + A'BCEF'
6.16 (a)
6.16 (b)
10000011, 3 0000-11, 3, 17, 19 0-00-1 A'C'D'F
20000101, 17 0-00011, 17, 3, 19 0-00-1
16 0100002, 3 00001-2, 3, 18, 19 0-001- A'C'D'E
32 1000002, 18 0-00102, 18, 3, 19 0-001-
300001116, 17 01000-16, 17, 18, 19 0100-- A'BC'D'
6.16
6.17 (a)
1 000001 1, 33 -00001* 11, 15, 43, 47 -01-11*
12 001100* 33, 35 1000-1*
33 100001 7, 15 00-111*
7 000111 11, 15 001-11
Prime Implicants: A'B'CDE'F', A'BCDEF', ABCDE'F',
B'C'D'E'F, AB'C'D'F, A'B'DEF, AB'D'EF, ABC'EF',
ABD'EF', ACD'EF, ABCD'E, B'CEF
Unit 6 Solutions
6.17 (b) Prime Implicants of G': AB'CE', AB'DE', AB'F',
BDF, BE'F, BD'E', CE'F, CD'E', DE'F, C'DE',
A'C'D'E, AC'D, D'F', C'F', BC', A'B, EF', BDE
Essential Prime Implicants of G': BC', AC'D, A'B,
EF', A'C'D'E
6.17 (a)
(cont.) (12)
(30)
(60)
1 7 11 12 15
A'BCDEF'
ABCDE'F'
B'C'D'E'F
X
X
33
(1, 33)
35 43 47 59 60
X
X
X
A'B'CDE'F'
X
Essential Prime Implicants: A'B'CDE'F',
ABCDE'F', B'C'D'E'F, A'B'DEF, B'CEF
G = A'B'CDE'F' + ABCDE'F' + B'C'D'E'F +
A'B'DEF + B'CEF + ACD'EF + AB'C'D'F
G = A'B'CDE'F' + ABCDE'F' + B'C'D'E'F +
6.18 (a) -0-1 = (1, 3, 9, 11), -01- = (2, 3, 10, 11),
--11 = (3, 7, 11, 15), 1--1 = (9, 11, 13, 15)
(b) maxterms = 0, 4, 5, 6, 8, 12, 14
(c) don't cares = 1, 10, 15
6.19
123456
1
X
X
7
X
Package
Using Petrick’s method:
(C1 + C3)(C2 + C3 + C5)(C1 + C4)(C1 + C5)
(C2 + C3)(C2 + C3 + C4)(C3 + C4)
= (C1C2 + C1C5 + C3)(C1 + C4C5)(C2C4 + C3)
Unit 6 Solutions
6.20
24 0011000 24, 28 0011-00 24, 28, 88, 92* -011-00*
28 0011100 24, 88 -011000 70, 86, 102, 118* 1--0110*
70 1000110 28, 92 -011100
88 1011000 70, 86 10-0110
(105) = (1101001) = ABC'DE'F'G
(a) r = ∏ M(1, 2, 3, 12) = (w + x + y + z′)(w + x + y′ + z)(w + x + y′ + z′)(w′ + x′ + y + z).
(b) prime implicant A: (0, 4) = w′y′z′
prime implicant C: (6, 7, 14, 15) = xy
prime implicant D: (8, 9, 10, 11) = wx′
(c) Using Petrick’s method
(A + G)(A + H)(B + H)(C + H)(B + C + H)(D + G)(D + F)(D + E)(D + E + F)(B + F)
6.21
6.22 (a) A minimum solution must cover (have an X in) the covered column, but then the minimum solution must cover
the covering column.
(b) If there is a minimal solution containing the covered row (P1 in this case), then it can be replaced by the covering
6.23 Prime implicants: AC, AD', AB, CD, BD, A'D
Minimum solutions: (AD' + CD); (AD' + BD);
(AB + BD); (AB + CD); (AB + A'D)
A B
C D 00 01 11 10
00
1
1
E
6.24 (a)
6.24 (b) A B
C D 00 01 11 10
00
G
X
E
69
Unit 6 Solutions
6.25 (a)
B C
D E
A
00 01 11 10
00
01
1
1
1
1
X
X
6.25 (b) Prime implicants: A'C'D', A'B, AB'D, A'C'E, ACDE,
BCDE, B'C'DE
Each minterm of the four variables A, B, C, D
expands to two minterms of the five variables
6.26 C D
E F 00 01 11 10
00
01
11
A
1
1
1
A
B
1
70
Unit 6 Solutions
