Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
Algorithms: Sequential, Parallel and Distributed 1-1
Chapter 27
Approximation Algorithms
At a Glance
Table of Contents
• Overview
• Objectives
• Instructor Notes
• Solutions to Selected Exercises
Algorithms: Sequential, Parallel and Distributed 1-2
Lecture Notes
Overview
In Chapter 27 we discuss the problem of finding efficient approximation algorithms for those
problems that are NP-hard. We define the notion of a k-approximation, and design k-
approximations for the Euclidean version of the traveling salesman problem, for the bin
packing problem, for the Steiner tree problem, and for the facility location problem.
Chapter Objectives
After completing the chapter the student will know:
• The definition a k-approximation to an optimization decision problem
• An O(n2) algorithm for a 2-approximation for the Euclidean version of the traveling
salesman problem, but that for any k, an algorithm giving a k-approximation for the general
traveling salesman problem would imply that P = NP
Instructor Notes
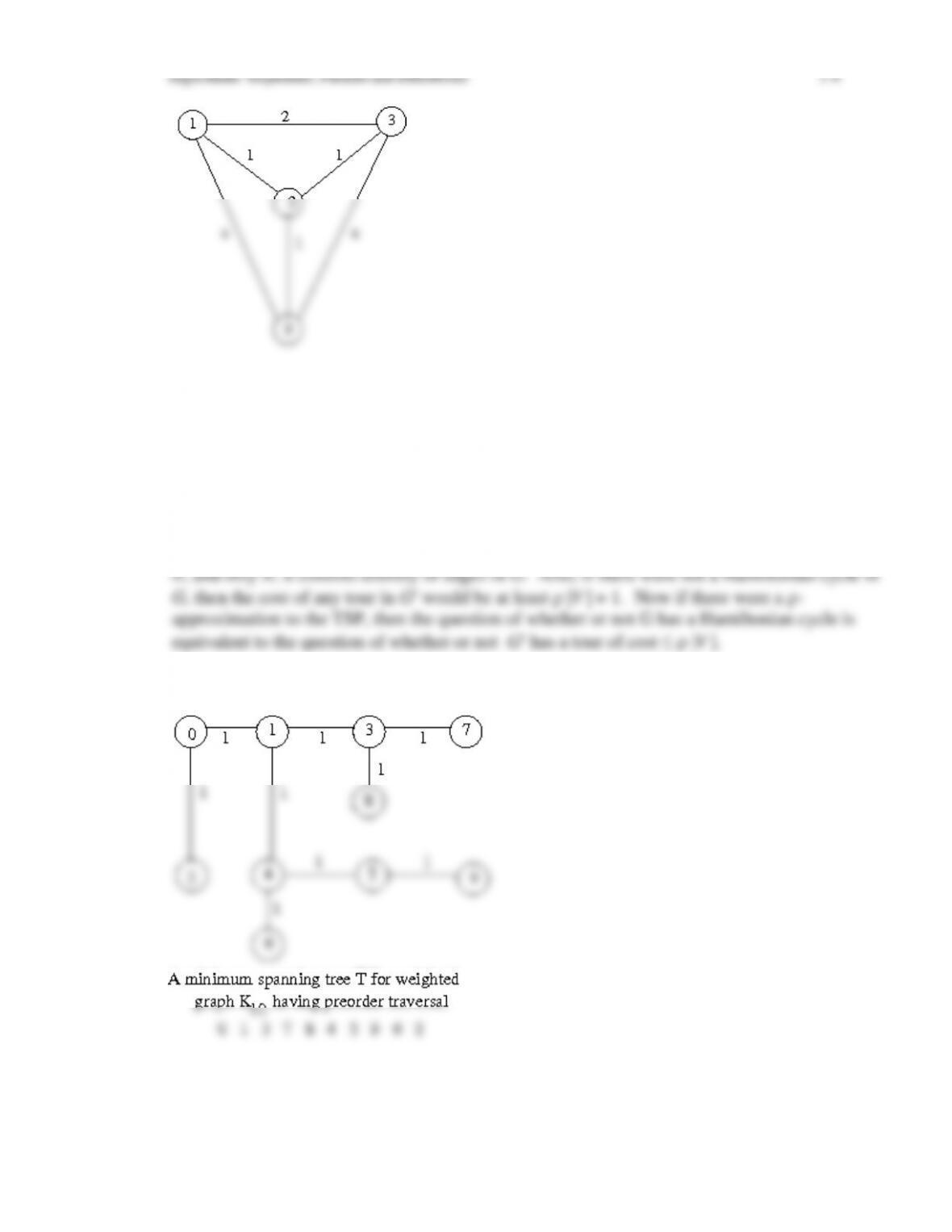
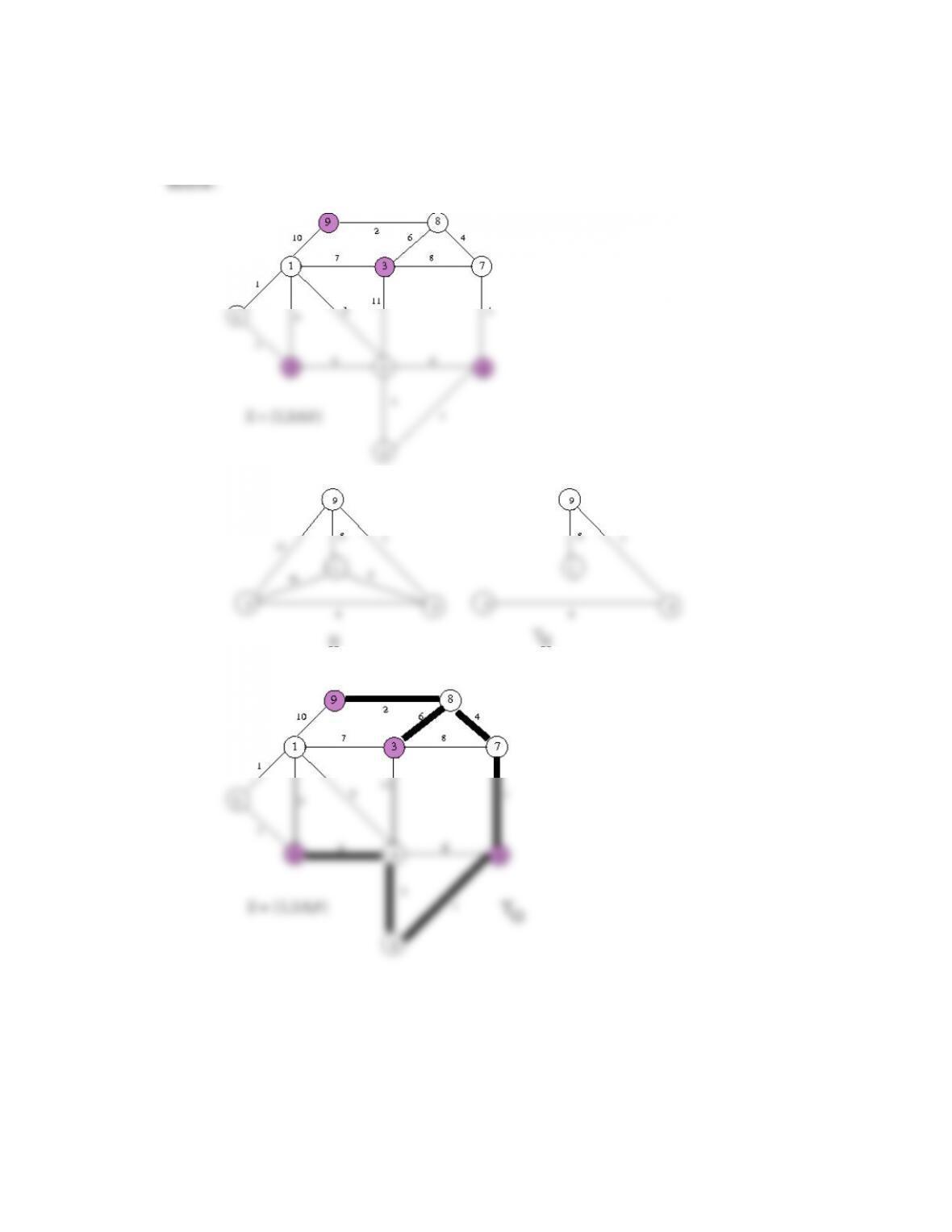
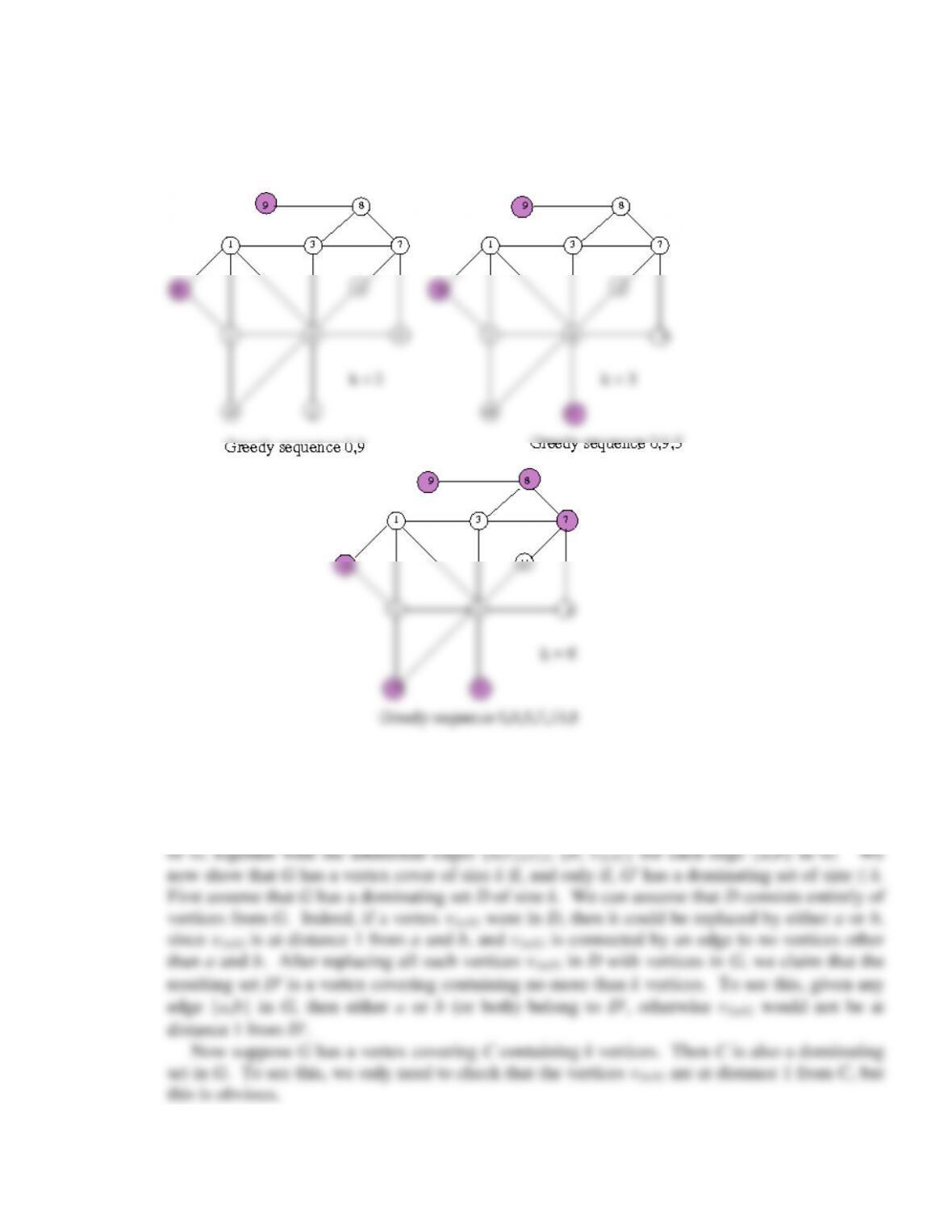
In Exercise 27.13 the graph shown was missing a weight on edge {3,8}. In doing the
exercise, we placed a weight of 6 on this edge for definiteness.
The discussion on p. 848 establishing the approximation result shown in formula (27.2.5) can
be improved. It would best proceed by first establishing the following two lemmas. The sets
A,B,C,D discussed are those defined on p. 848. The proof of the Lemma 1 follows the exact
same lines that that given for case 1 on p. 848.
Lemma 1. Suppose all but at most one of the m bins in a bin packing are at least 2/3 full.
Then m ≤ m* + 1.
Proof. If si denotes the amount in bin i, we have:
m
1
m
Lemma 2. Suppose in the first-fit decreasing bin packing that there is a bin that only contains
objects from the set D. Then all but at most one of the m bins in a bin packing are at least 2/3
full.
Solutions to Selected Exercises
Section 27.1 The Traveling Salesman Problem
27.2 Of course it is required that n ≥ 4. We give an example for K4. It is straightforward to
generalize to Kn for an arbitrary n > 4. In the figure below, growing a minimum
27.3 Let G = (V,E) be any instance of the Hamiltonian cycle decision problem. Consider the
instance of TSP on the complete graph G = (V,E) with the following weighting: (u,v) = 1 if
uv E, otherwise (u,v) = |V | + 1. Note that a Hamiltonian cycle in G would have cost |V |,
Algorithms: Sequential, Parallel and Distributed 1-5
Section 27.2 Bin Packing
27.6 Let si denote the sum of the sizes of all of the objects placed in bin i, 1 ≤ i ≤ m*. Then
0 < si ≤ 1 and
*1
*
1
*
1mFs m
i
m
ii=== ==
. But since m* is an integer, it follows that
27.7 a. Next fit uses 5 bins Bi, with the placement:
27.8 a. First fit uses 5 bins Bi, with the placement:
27.9 a. First fit decreasing uses 4 bins Bi, with the placement:
B1: .9, .1 B2: .7, .15, .1 B3: .6, .4 B4: .4, .35
.
27.11 Using the two lemmas discussed in the Instructor Notes above, we can assume that no
bin contains only objects from set D. Note that in this case, using the first-fit decreasing
packing the number of bins would remain the same if the set D is empty. Thus, we can assume
that our objects only consist of objects from A, B, and C. In the latter case, the first-fit
Algorithms: Sequential, Parallel and Distributed 1-7
Section 27.3 The Steiner Tree Problem
27.13 Note: There was a missing weight on edge {3,8}, which we took to be 6 in the figure
Algorithms: Sequential, Parallel and Distributed 1-8
Section 27.4 The Facility Location Problem
27.16
27.17 We show Vertex Cover Dominating Set. Let G be any graph, and suppose we ask
whether G has a vertex cover C of size k.. Construct a graph G as follows. The vertex set of
G will consist of all vertices of G, except isolated vertices. For each edge {a,b} in G, we also
add a vertex v{a,b} to G. The edge set of G will be a bunch of triangles consisting of all edges
27.18 We show that the Dominating Set ρ-approximation to the facility location with ρ < 2.
Let G be a graph and we ask whether G has a domination set of size ≤ k. Construct a
complete graph G from G by adding all edges not in G. Then define a weighting on G by
27.19 First note that VertexCoverApprox actually produces a vertex cover, since an edge is
only deleted when it is adjacent to a vertex that has already been covered by an edge in the
