Algorithms: Sequential, Parallel and Distributed 1-1
Chapter 25
Lower Bound Theory
At a Glance
Table of Contents
• Overview
• Objectives
• Instructor Notes
• Solutions to Selected Exercises
Algorithms: Sequential, Parallel and Distributed 1-2
Lecture Notes
Overview
In Chapter 25 we discuss various techniques for establishing lower bounds for the complexity
of algorithms. In particular, we discuss decision trees and comparison trees, adversary
arguments, and information theoretic arguments. We establish sharp lower bounds for the
problem of finding both the maximum and minimum values in a list, as well as the problem of
finding the largest and second largest value. We also establish an order-optimal lower bound
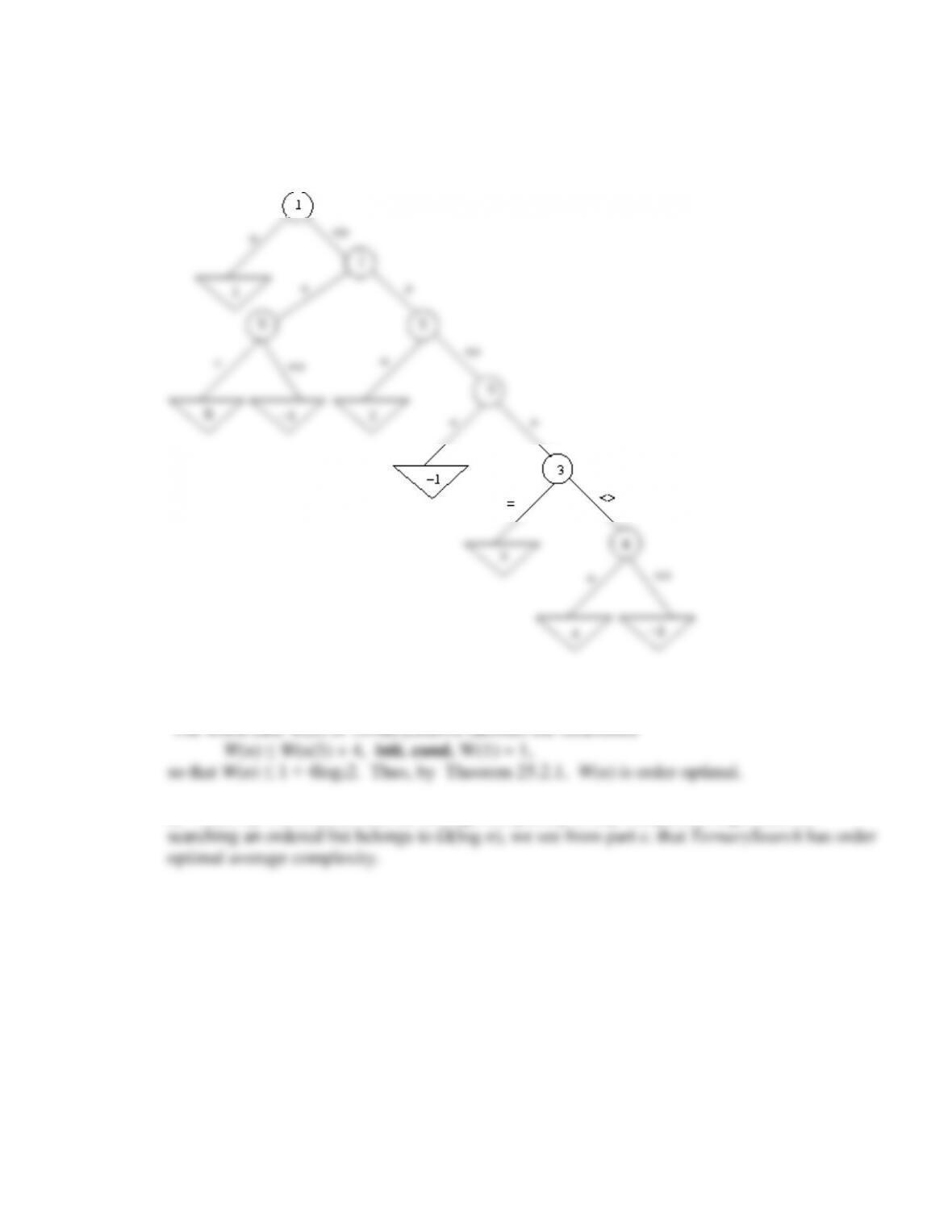
for the problem of finding the median value in a list. We finish the chapter with determining a
lower bound for the problem of sorting a list of size n in parallel sorting using n processors.
Chapter Objectives
After completing the chapter the student will know:
• The various techniques for establishing lower bounds for the complexity of algorithms,
including counting arguments, decision and comparison trees, adversary arguments, and
information theoretic arguments
• A lower bound for finding both the maximum and minimum values in a list, and an optimal
algorithm for this problem
Instructor Notes
Except for the material on parallel algorithms, the remainder of the material in this chapter can
be covered any time after the first four chapters are covered. For example, the instructor may
wish to discuss lower bound results using decision and comparison trees for searching and
Algorithms: Sequential, Parallel and Distributed 1-3
Solutions to Selected Exercises
Section 25.1 Basic Terminology and Techniques
25.1 a. We prove that there exists a set of flips that sorts any given stack of pancakes by
induction on the number n of pancakes.
Basis step: n = 1. Obvious.
Induction step: Assume the result is true for n – 1 pancakes, and consider a set of n pancakes.
b. The algorithm simply implements the procedure described in part a. The function FindMax
included in the algorithm PancakeSort performs a linear search to find the index of a largest
element in the list L[0:k].
i
FindMax(L[0:k])
//flip L[0:i] so that largest element in L[0:k] is placed in position 0
for j
0 to i/2 do
interchange(L[j], L[i – j])
endfor
//flip L[0:k], so that largest element in L[0:k] is placed in position k
c. Consider a list L[0:n – 1] consisting of alternating 0s and 1s, ending with a 0. Note that
there are n – 1 positions in the list where L[i] ≠ L[i + 1]. Call such a position a change position.
Algorithms: Sequential, Parallel and Distributed 1-4
d. When the largest pancake is found and brought to the top of the stack by a flip, if the non-
burnt side is facing up, then a flip of this pancake is made so that the non-burnt side is facing
25.2 To simplify the discussion, assume that n is a multiple of k + 1, n = m(k + 1). Let L[0:n –
1] be a list containing the integers 1, 2, …, n, divided up into m blocks, where the jth block
25.3 InsertionSort makes kn/2 + n/(k + 1) comparisons on the list described in the previous
exercise, so it does not quite achieve the lower bound established in that exercise, although it is
order-optimal.
25.4 We prove that BinarySearch2 is correct by induction on k = high – low.
Basis step: k = 0. Then low = high, and X is compared to L[low] and the correct result is
returned by BinarySearch2.
Induction step: Assume that BinarySearch2 is correct when called with all values of high –
25.6
a.
function TenarySearch(L[0: n – 1], Low, High, X) recursive
Input: L[0: n – 1] (a list of size n), Low,High (integers), X (a search element)
Output: an index i, Low ≤ i ≤ High, such that L[i] = X, -1 if no such index exists.
return (Low)
else
if X = L[High] then
return (High)
else
return (TenarySearch(L[0: n – 1], Third + 1, TwoThirds – 1, X))
else
return (TenarySearch(L[0: n – 1], TwoThirds + 1, High, X))
endif
end TenarySearch
Algorithms: Sequential, Parallel and Distributed 1-6
b. This should have asked for the comparison tree for n = 5 instead of n = 25 This tree is as
follows, where internal nodes show the index in the list L[0:4] that the search element is
compared to, and the leaf nodes show what is returned.
c.
d. Since by Theorem 25.2.2, the average complexity of any comparison algorithm for
25.7 For convenience of pseudocode and analysis, we assume in TernarySearch2 that n = 3k.
a.
function TenarySearch2(L[0: n – 1], Low, High, X) recursive
Input: L[0: n – 1] (a list of size n = 3k), Low,High (integers), X (a search element)
Output: an index i, Low ≤ i ≤ High, such that L[i] = X, -1 if no such index exists.
c. The worst case W(n) of TernarySearch2 satisfies the recurrence
d. Since by Theorem 25.2.2, the average complexity of any comparison algorithm for
25.8 Alter LinearSearch by first making the comparison of the search element X with L[0], and
25.9 The comparison tree T for any algorithm that determines whether there is an index i such
that L[i] = i in a sorted list of integers L[0: n – 1] must have n + 1 leaf nodes corresponding to
25.10
ennnneenn nn 2222
)12/(1
2logloglog)2/1()2(log)2/1()/(2log −++=
2ln
n
25.11 a. A list of integers where adjacent elements in the list differ by at most 1 satisfies an
intermediate value property, i.e., if i < j, and X is any value strictly in between L[i] and
L[j], then there is a k such that i < k < j such that L[k] = X. Thus, BinarySearch works for
25.12 With each comparison between two elements, as before we say that the larger of the two
elements wins the comparison, and the smaller loses. Each comparison results in exactly one
25.13 The following algorithm uses the optimal number n +
2
log n
– 2 of comparisons of
between list elements. However, there is a fair amount of overhead due to auxiliary arrays. We
j
n
for i
0 to n – 1 do //initialize arrays
Winners[0: i]
i
Start[i]
i //array of pointers to nodes of type LoserNode
→
→
Winners[m/2]
Winners[m]
End[Winners[m]]
→
Next
P
P
→
Loser
L[Winners[m + 1]]
endif
endfor
→
25.14 For L[0: n – 1] a list of distinct elements where n is even, there are two elements M1 <
M2 with the property that there are (n – 2)/2 elements smaller than M1 and (n – 2)/2 elements
larger than M2 (so that the median is usually taken to be (M1 + M2)/2). As in the proof of
25.15 We show that for any algorithm for merging two ordered sublists of size n/2, its worst
case cannot be such that O(W(n))
O(n). For assuming the contrary, using the algorithm as
25.16 Divide the list L[0:n – 1] into n1/2 sublists of size n1/2. Assigning n1/2 processors to
each sublist, perform a parallel recursive call (i.e., a parallelcall) to MinCRCW2 to compute
the minimum in each sublist. Now call MinCRCW to find the minimum of these n1/2 minimums
in constant time (one parallel comparison step). Clearly, the (parallel) worst-case complexity
