Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
Algorithms: Sequential, Parallel and Distributed 1-1
Chapter 21
Balanced Search Trees
At a Glance
Table of Contents
• Overview
• Objectives
• Instructor Notes
• Solutions to Selected Exercises
Algorithms: Sequential, Parallel and Distributed 1-2
Lecture Notes
Overview
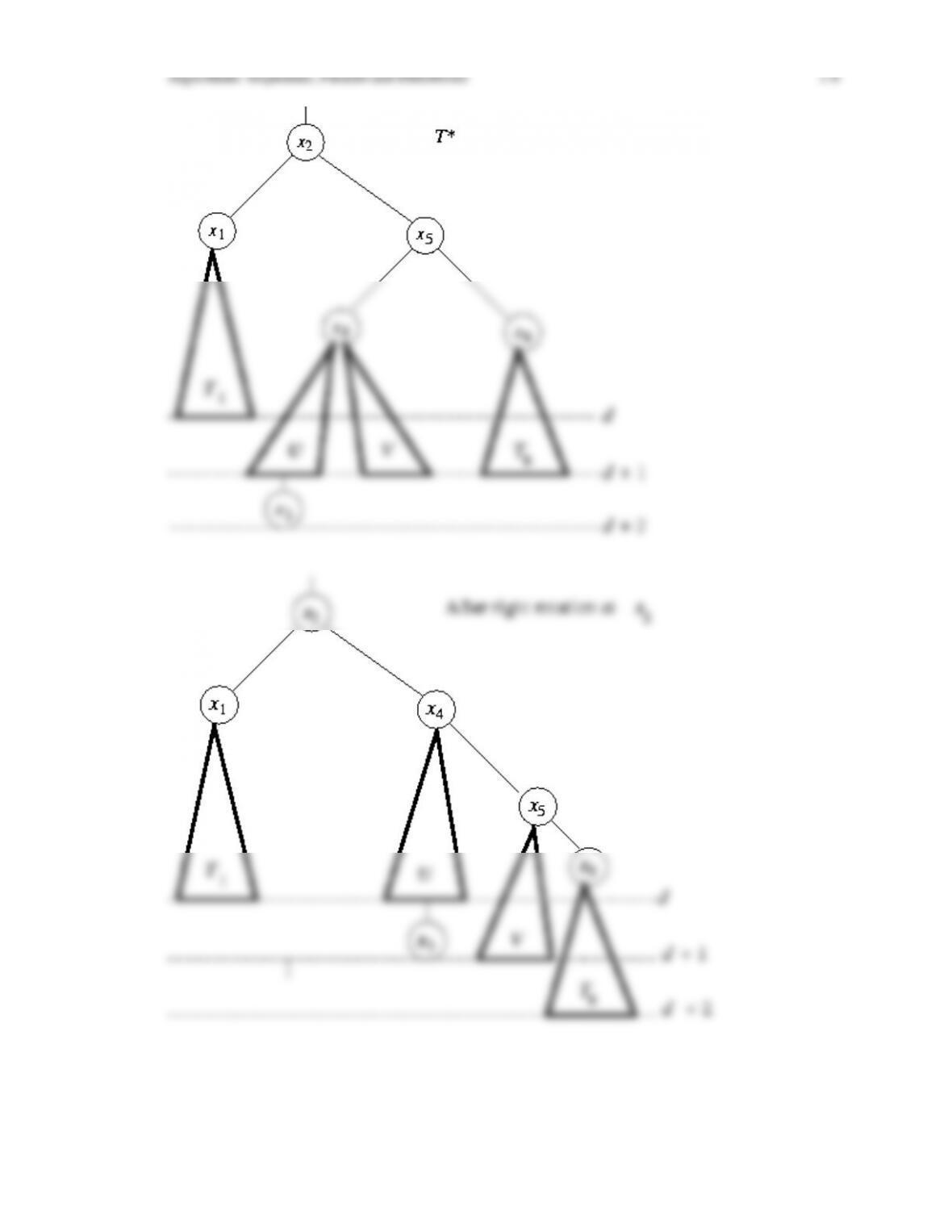
In Chapter 21 we introduce the notion of a balanced binary search tree, and show how rotations
in such trees can be used to help restore balance after nodes have been inserted or deleted. We
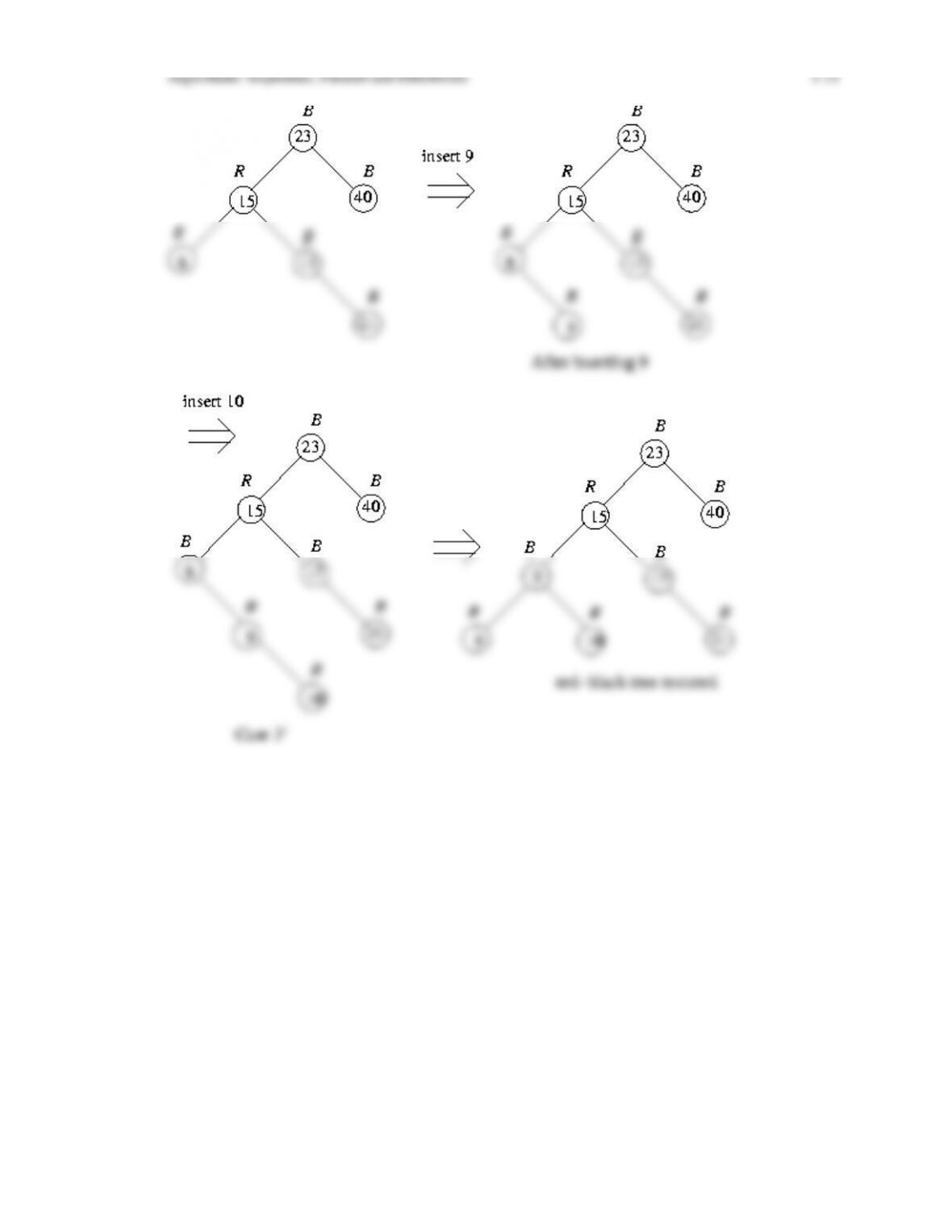
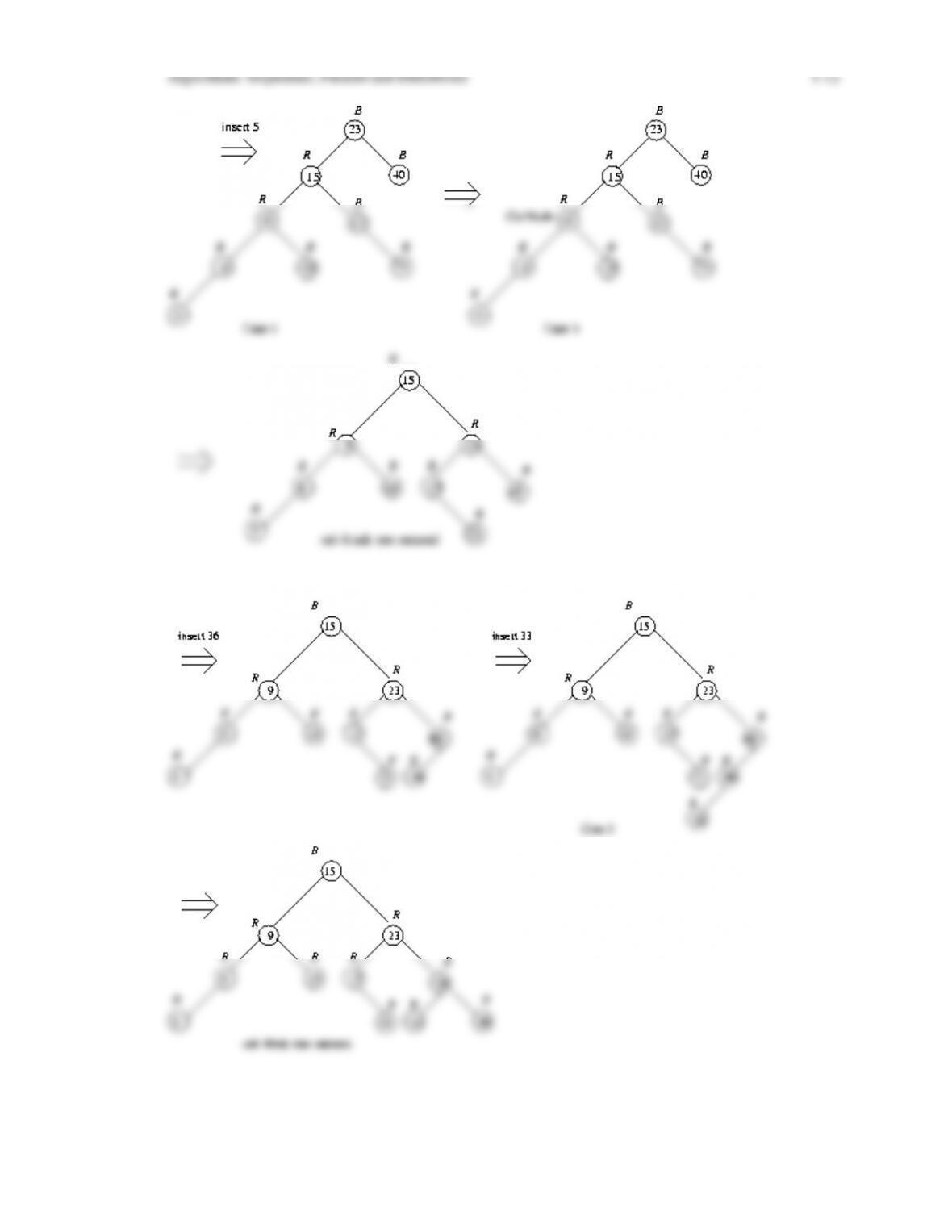
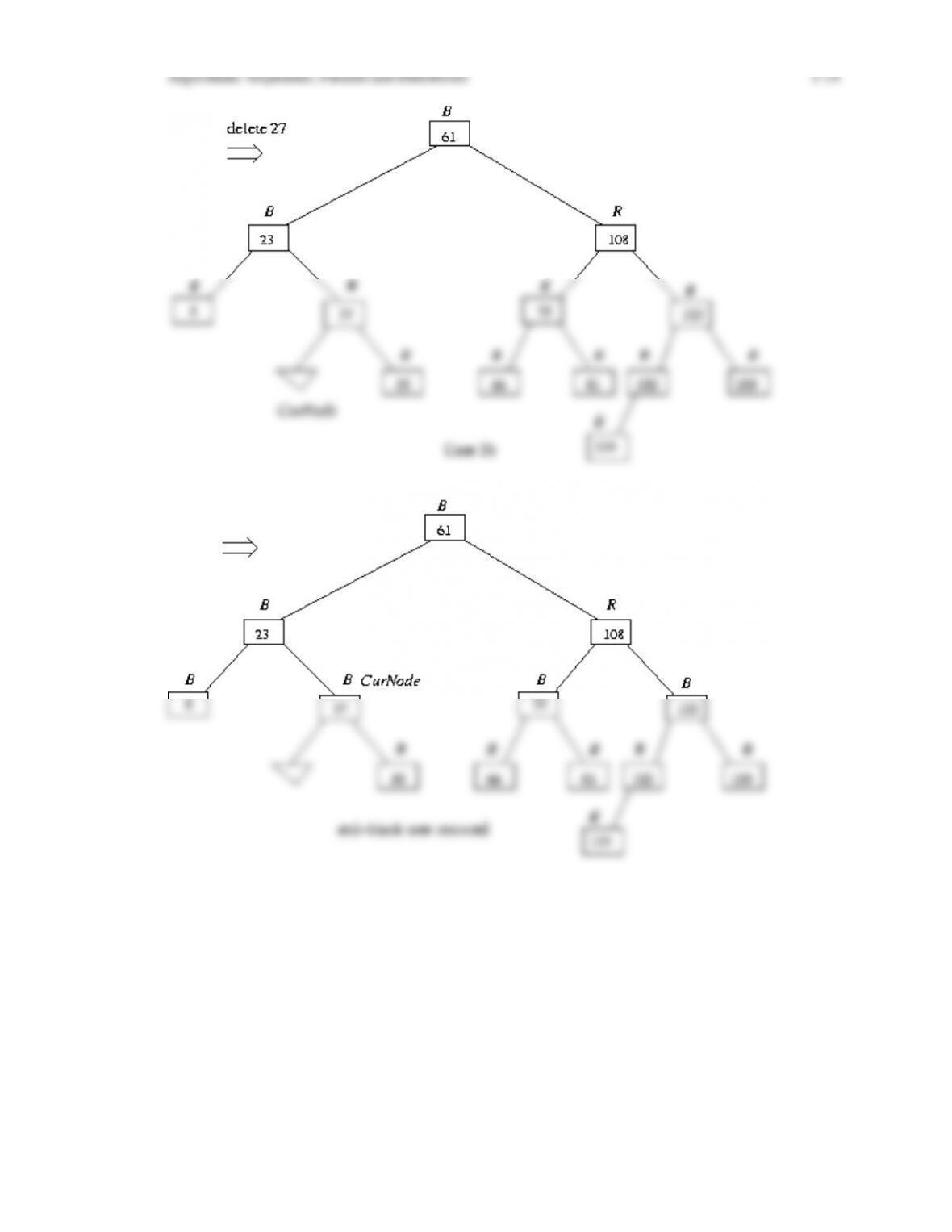
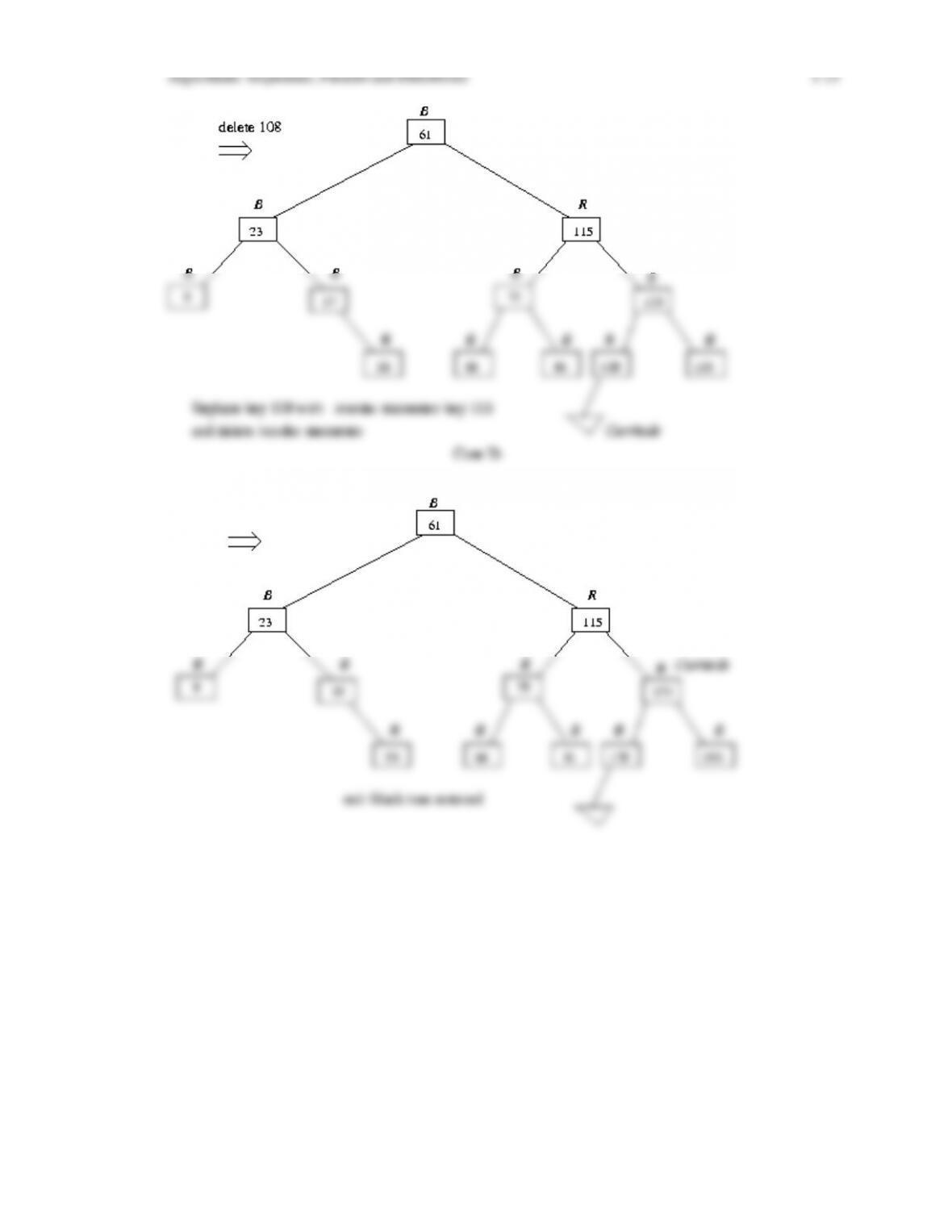
define the notion of an AVL tree and a red-black tree, and prove that the depth of a red-black
tree is logarithmic in the number of nodes in the tree. We then discuss algorithms for inserting
and deleting nodes in a red-black tree, including giving transition diagrams that show how
these algorithms proceed through the various cases until balance is restored. We finish the
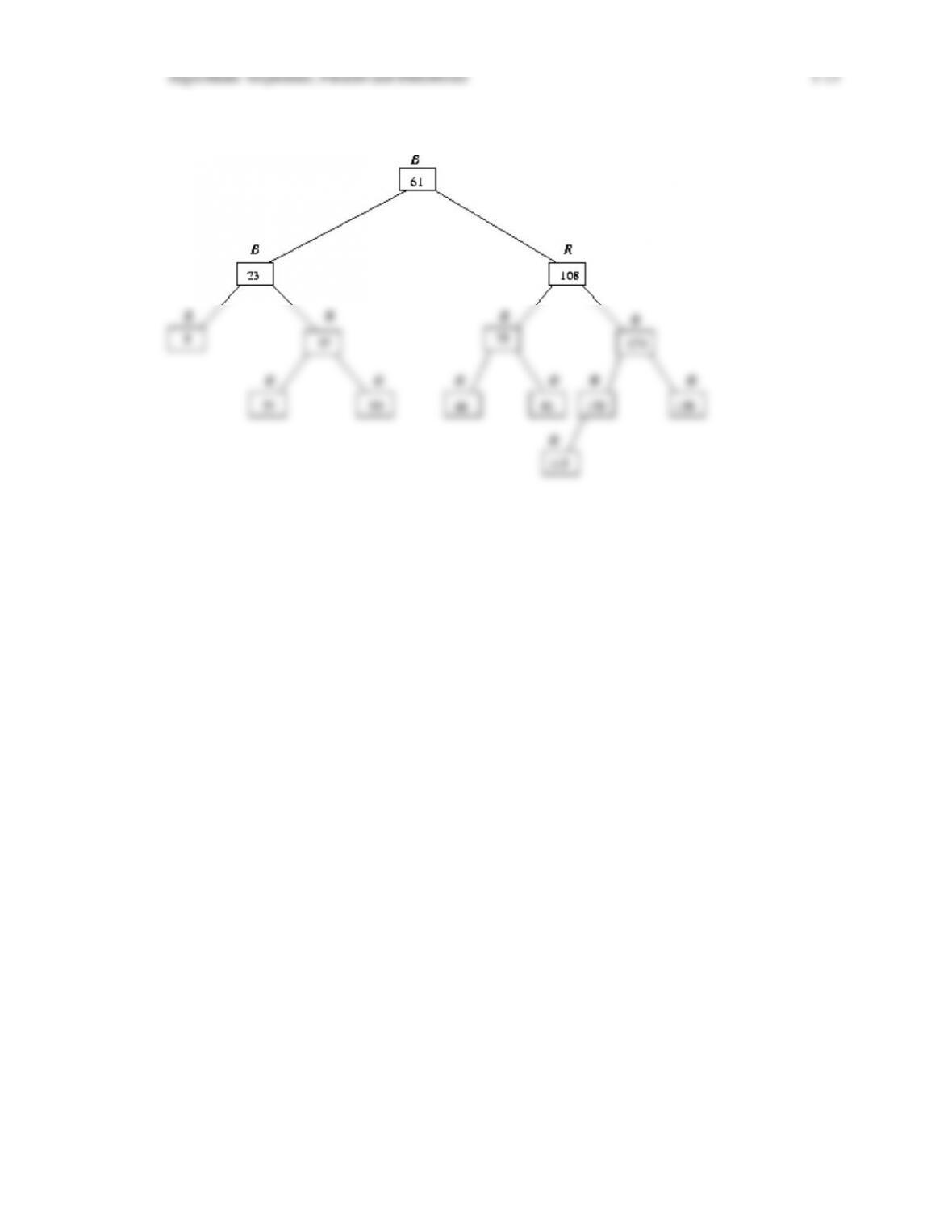
chapter with a discussion of the B-tree multiway search tree, which is a useful ADT for
maintaining externally stored databases.
Chapter Objectives
After completing the chapter the student will know:
• The definitions of AVL and red-black trees
• The notion of a rotation in a binary search tree, and its role in restoring balance in AVL and
red-black trees
Instructor Notes
The algorithms for inserting and deleting elements in a red-black tree are straightforward, but
cumbersome in detail. Certainly one would not expect the student (or the instructor!) to
memorize the various cases and what procedures are followed depending on these cases.
Algorithms: Sequential, Parallel and Distributed 1-3
Solutions to Selected Exercises
Section 21.2 Rotations of Binary Search Trees
21.1
function CreateBinSrchTree(i, j) recursive
Input: i, j (integers between 0 and n – 1, inclusive)
Output: creates a binary search tree for the keys Ki, Ki+1, …, Kj and returns a pointer to the root
21.2 Except for whatever is needed to assign information to the field Info, only three
statements need to be added to the pseudocode for InsertBinSrchTree given on p. 138 in the
21.3 That an inorder traversal of a binary search tree T visits the nodes in increasing order
of the keys is shown in the solution to Exercise 4.36 of Chapter 4. Thus, we only need show
that if the inorder traversal visits the nodes of the binary tree T in increasing order of the keys,
21.4
procedure RotateLeft(Root,Node)
Input: Root (→BinaryTreeNode) //points at root of a binary tree T
Node (→BinaryTreeNode) //points at node where rotation takes
//place
21.5 We prove that the depth d(T) of any AVL-tree on n nodes belongs to O(logn) by proving
the following proposition.
Proposition Let d = d(T) be the depth of an AVL tree T. Then each level of T is full for all
levels ≤ d/4.
21.6 There are a number of cases that occur when an insertion of an element into an AVL tree
T destroys the AVL property. Suppose that T* is the smallest subtree (that, is, rooted at the
deepest level) where the insertion violates the AVL property of T*. A straightforward case-by-
case analysis shows that a single rotation of T* will restore the AVL property of T*, and at the
same time restore the AVL property of the entire tree, except for two mirror-image cases, as
Algorithms: Sequential, Parallel and Distributed 1-7
Section 21.3 Red-Black Trees
21.7 Consider any two paths P1 and P2 from the root to leaf nodes in the red-black tree. Then
P1 and P2 have the same number b of black nodes. Let r1 and r2 be the number of red nodes in
21.9 In the pseudocode for RBCorrect(iii)OrMoveUpL, we assume that the parameter Node in
the call to DeleteBinSrch2 is an input-output parameter, so that after the call it is the node
actually deleted, which will be the inorder successor of the node containing the key to be
deleted in case the latter node has two non-null children. Also, DeleteBinSrch2 has added the
output parameter CurNode to the parameter list of DeleteBinSrch, where CurNode is the
.and. SRC→Color = black then //Case 1
Parent→Color ← red
Sibling→Color ← black
RotateLeft(Root, Parent)
//Case 3
Sibling→Color ← red
if Sibling→Color = black .and. SRC→Color = red then //Case 4
SRC→Color ← black
21.10 a. We only consider the unprimed cases, as the primed cases are similar. Our arguments
are based on Figure 21.9, which while it uses specific keys for ease of discussion, nevertheless
Case 1. Note that the number of black nodes of on paths passing through node 23 and going on
to either node 17 or node 55 not changed after the transformation. Note also that a path going
child 5. After the transformation, all paths going through 12 are deficient, so that the violation
Case 2b. After the transformation, all deficient paths add one black node (that is, they are no
Case 3. A simple check shows that all non-deficient paths have the same number of black
Case 4. (Deficient) paths going through 5 pick up one black node after the transformation, so
they are no longer deficient. A simple check shows that all non-deficient paths have the same
number of black nodes (that is, remain non-deficient) after the transformation. Since no other
violations of the red-black properties are introduced, the red-black property is now restored.
b.
if Node→LeftChild ≠ Sentinel .and. (Node→LeftChild)→Color = red then
(Node→LeftChild)→Color = black
return
endif
if Node→RightChild ≠ Sentinel .and. (Node→RightChild)→Color = red then
21.11
21.12
