Algorithms: Sequential, Parallel and Distributed 1-1
Chapter 16
Parallel Design Strategies
At a Glance
Table of Contents
• Overview
• Objectives
• Instructor Notes
• Solutions to Selected Exercises
Algorithms: Sequential, Parallel and Distributed 1-2
Lecture Notes
Overview
In Chapter 16 we discuss three widely used tools in parallel algorithm design: parallel
prefix, pointer jumping and parallel matrix multiplication. We discuss parallel prefix
computations on a PRAM, complete binary tree and two-dimensional mesh and
applications of such computations to designing parallel algorithms for the knapsack
problem and carry-lookahead addition. We then discuss pointer jumping and its
application to computing a minimum spanning tree on a CREW PRAM. Finally, we
discuss algorithms for matrix multiplication and matrix powers on a CREW PRAM, which
we apply to obtain an O(log2n) algorithm for the all-pairs shortest path problem in a
weighted digraph.
Chapter Objectives
After completing the chapter the student will know:
• The parallel prefix paradigm and its implementation on a PRAM, complete binary tree
and two-dimensional mesh
• The pointer jumping technique implemented on a CREW PRAM
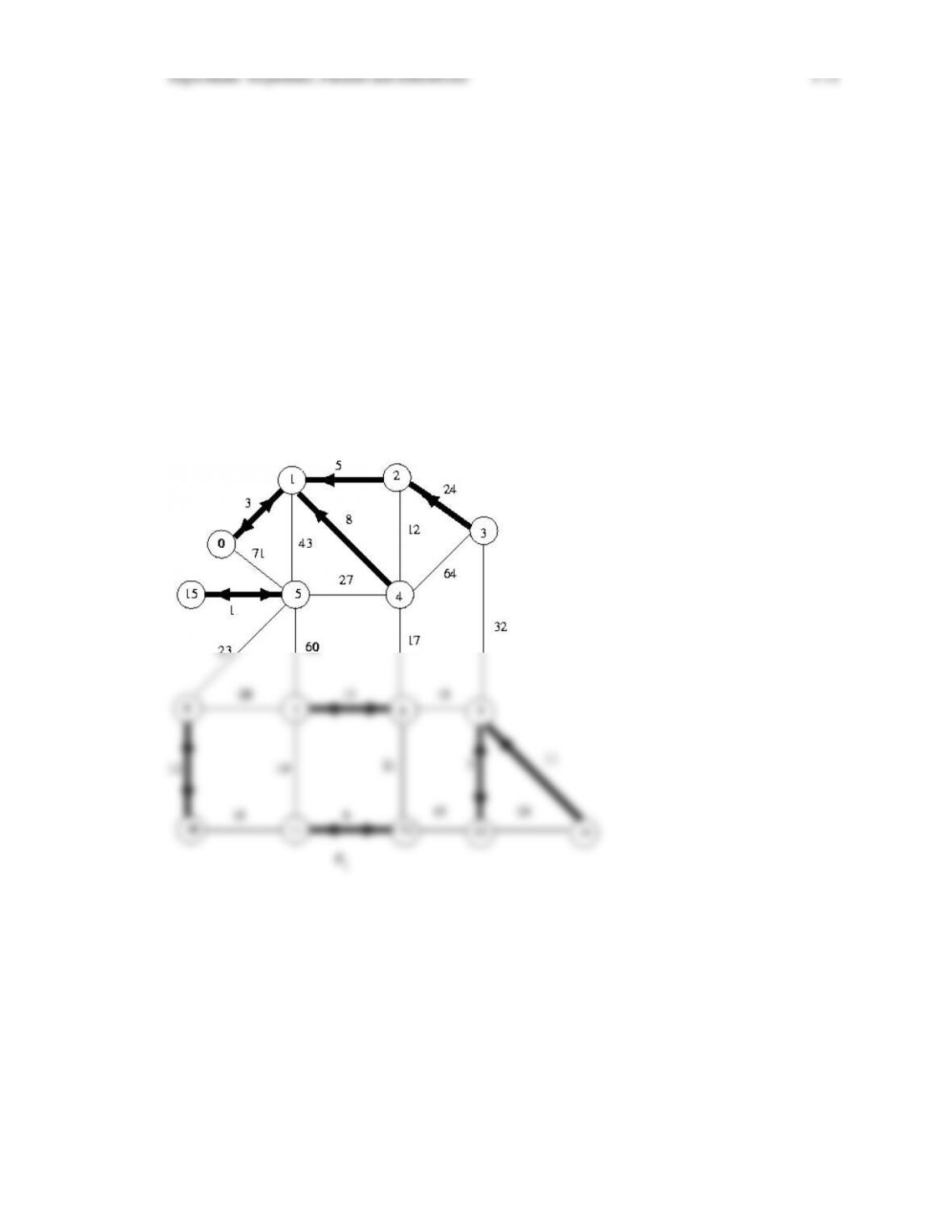
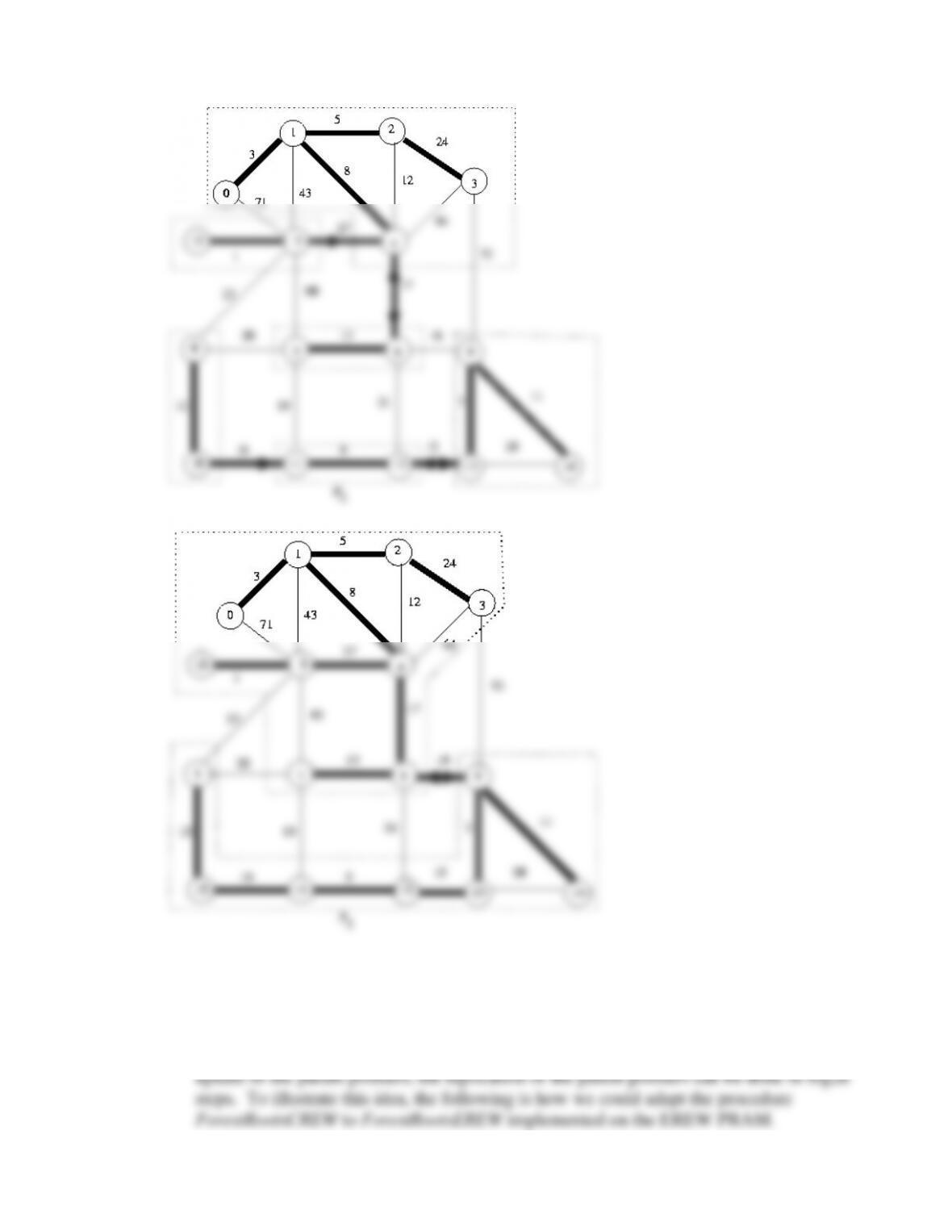
• A parallel algorithm for computing a minimum spanning tree and how pointer jumping
is used to acheive polylogarithmic complexity of the algorithm on a CREW PRAM.
• Matrix multiplication on a CREW PRAM
• Application on parallel prefix to the knapsack problem and carry-lookahead addition
• Application of matrix powers to the all-pairs shortest path problem in a weighted
digraph.
Instructor Notes
The application of the parallel prefix method to solve the carry-lookahead addition problem in
O(logn) time is surprising, since at first glance this problem seems essential sequential. Indeed,
to compute the proper entry for the ith bit position definitely requires knowing the appropriate
carry digit resulting from the previous bit positions. The surprising thing is that all n carries
can be computed in O(logn) time. Apparently this surprising result was used in the early days
of parallel computing to convince the Federal Funding agencies to support parallel algorithms
and architectures research.
The parallel algorithm for the minimum spanning tree problem presented in this chapter is
actually a parallelization of the sequential algorithm for this problem given by the Polish
Algorithms: Sequential, Parallel and Distributed 1-3
mathematician Barůvka in 1926. We also give a distribution version of this algorithm in
Chapter 19.
Solutions to Selected Exercises
16.1 Let Sik denote X[i]
…
X[k], 0 ≤ i < k ≤ n – 1, where Sii = X[i]. The correctness of
PrefixPRAM follows from the following three loop invariants that hold after j iterations of
the while loop, 0 ≤ j ≤
n
2
log
:
3. k = 2j.
We establish these loop invariants using induction on j.
Basis step: j = 0. Since Prefix[i] is initialized to X[i] = Sii, 0 ≤ i ≤ n – 1, conditions 1 and 2
– 1. Hence, by our induction hypothesis, for 2j-1 = k ≤ i ≤ min{2j – 1, n – 1}, Prefix[i] is
replaced by
Prefix[i – 2j-1]
Prefix[i] = S0, i – 2j–1
Si – 2j-1+1,i = S0i,
whereas for min{2j, n – 1}+ 1 ≤ i ≤ min{2j – 1, n – 1}, Prefix[i] is replaced by
n
log
2
n
log
n
log
2
2
n
log
2
16.2 In the following pseudocode for PrefexPT, we use the same conventions for indexing
processors as used in the pseudocode for MinPT that was given in the solution to Exercise
15.10. However, in this problem we assume that the n numbers x0, x1, … , xn-1,are stored in
the distributed variable X of the processor tree PT2n-1, so that xi is stored in leaf processor’s
memory location Pbin(k, i):X, n = 2k, 0 ≤ i ≤ n – 1.
Algorithms: Sequential, Parallel and Distributed 1-4
procedure PrefixPT(X,n)
X ← X + Y
end in parallel
endfor
//Phase 2: for leaves, add numbers in siblings and leave result in right sibling
for Pbin(k – 1, j), 0 ≤ j ≤ 2k – 1 – 1 do in parallel
Pbin(i, j)1:X ← Pbin(i,j):X
Pbin(i, j)0:X ← 0
end in parallel
//Phase 4: Compute binary fan-out sums
for i ← 1 to k – 1 do
16.4 To show that x
(y
z) = (x
y)
z for all x,y,z
{p,s,r}, note from the table on p.
524 in the text that when z is p, both products will evaluate to x
y. Also note that when z
16.5 Since S0i = s
σ1
…
σi, and p acts as an identity element for
, it follows that S0i
is either r or s for each i = 0, …, n. We prove that ci = 0 if S0i = s, and ci = 1, otherwise, by
induction on i.
16.6 The algorithm PrefixBinaryTree is a generalization of the algorithm PrefixPT to an
arbitary binary tree T. Thus, we give only a high-level description. In the following
discussion, we assume that the operands are numbers stored in the leaves of the tree in
traversal order, and that the operation is additon. The algorithm PrefixBinaryTree consists of
4 phases. In phase 1, fan-in sums are computed using a postorder traversal. We assume that
each have fewer than n nodes. It is easy to verify that PrefixBinaryTree with input tree T
works on those nodes in LT exactly as PrefixBinaryTree works with input tree LT, except
that before phase 3, the root node of LT contains the prefix sum corresponding to the sum of
all of the numbers in the leaves of LT. During phase 3 the latter prefix sum is transferred to
the root node of RT, or added to the single number in RT in case RT consists of a single
Algorithms: Sequential, Parallel and Distributed 1-6
16.8 a) It is clear from the definition of
¯ given in Figure 11.15 that
(a
¯ b)
¯ |c = a
¯ (b
¯ |c) = |c.
¯ agrees with on the set SS. Hence, the following two verifications complete
¯:
16.10 a) The following pseudocode solves the packing problem on the EREW PRAM.
Procedure PackPRAM(A[0:n – 1], Color[0:n – 1])
Model: EREW PRAM with p = n processors
Input: A[0:n – 1] (array of size n)
Color[0:n – 1] (Red,Blue coloring of the elements of A)
end in parallel
//Compute prefix sums
PrefixPRAM(PrefixR[0:n – 1])
PrefixPRAM(PrefixB[0:n – 1])
L ← PrefixR[n – 1]
Temp[PrefixR[i] – 1] ← A[i]
endif
if PrefixB[i] PrefixB[i – 1] then
Temp[PrefixB[i] + L – 1] ← A[i]
endif
coloring, invoke PackPRAM to pack the array. Then repeat the process m – 1 times, proceeding
from the 2nd least significant digit to the most significant digit, where at the ith step the coloring
is with respect to the ith least significant digit. The resulting algorithm, RadixSortPRAM, has
(mlogn) complexity.
c) The algorithm for k colors and array A[low,n] is recursive (low = 0 on initial call). If k = 1,
16.11 The parallelization is recursive, where with each recursive call, elements in the sublist
corresponding to the call are colored red and blue according to whether the digit in position i
in the binary string is 0 or 1, respectively. The initial call has i being the most significant
16.12 In the following pseudocode, we assume that the nodes in the forest are indexed by 0,1,2,
, n – 1, and root nodes r of the forest maintained by Parent[0:n – 1] are determined by the
condition Parent[r] = – 1.
Algorithms: Sequential, Parallel and Distributed 1-8
procedure Roots(Parent[0:n – 1], R[0:n – 1])
for i ← 0 to n – 1 do
r ← i
while R[r] = – 1 do
r ← Parent[r]
endwhile
16.13 No speedup over a sequential algorithm is possible unless the nodes in the linked list are
16.14 a. Since we know that the list has size n, and Start points to the beginning of the linked
list maintained by Next[0:n – 1], we merely set Distance[Start] = n – 2, and then march down
the linked list setting the distance for each node encountered to be one less than the previous
node.
b. Using pointer jumping on the EREW PRAM, we obtain an O(log n) algorithm for list
time updating the array Distance so that Property A remains valid for the new sublists. After
log2n parallel pointer-jumping steps, all the linked sublists maintained by Next consist of
singletons. Since Property A has been maintained for these sublists, Distance[0:n – 1]
necessarily has all the correct distances. We first give the pseudocode, and then discuss its
correctness, which amounts to showing that Property A is a loop invariant of the while loop.
else
Distance[i] ← 1
endif
end in parallel
while Next[Start] ≠ – 1 do
successor’s value Distance[Next[i]] to its own value Distance[i] before jumping around it by
changing Next[i]. Hence, the sum of the values Distance[j] for all indices j in the linked sublist
headed by i will clearly not change in the new linked sublist headed by i resulting from
performing the update action of any given execution of the while loop. In other words, while
the linked sublist headed by i is altered, the sum of the values Distance[j] in the sublist is left
16.15 Since we know the size of the list is n, we know that the while loop in ListRankPRAM
16.16 In the following pseudocode, we assume that the end of the linked list maintained by
Next[0:n – 1] is determined by the condition Next[i] = – 1, and that Start points to the first
node in the linked list.
procedure PrefixLinkListPRAM(X[0:n – 1], Next[0:n], Start)
Model: EREW PRAM with p = n processors
16.17 Given G = (V,E), and the weighting w(e) on the edges, where e = {i,j}, i < j, define the
new weighting to be the vector (w(e),i,j), where the ordering on the vectors is lexicographical,
and we sum the vectors using ordinary vector addition. Clearly, distinct edges have distinct
16.18
Algorithms: Sequential, Parallel and Distributed 1-12
16.19 The algorithm MSTCREW uses pointer jumping to find the leader of each supervertex,
as well as to the find the minimum edges adjacent to each supervertex vertex. Since this
may involve concurrent reads, it is enough to replicate the parent of each node throughout
an array of size n, so that each node j wanting to access the parent of a given node I can red
this value in position j of the array containing the replication of the parent of i. After each
16.20 Given an input graph G on n vertices, create a complete graph G* on n vertices where
16.21 Assume that the tree has vertices 1,2,…,n, and is given by the parent array Parent[1:n],
where Parent[r] = r determines the root node r. Note that given any vertex i, the problem of
determining the depth of i is equivalent to finding the ranking of i in the list i, Parent[i],
Parent[Parent[i]], …,Parentdepth(i)[i]=r. Thus, the following pseudocode
emulates the code for the list ranking problem.
16.22 In the solution to Exercise 16.20 we discussed how MSTCREW could be used to
16.23 MatVecProdCREW is the special case of MatMultCREW where the matrix B is a column
vector. To adapt it to an EREW PRAM, first broadcast B throughout a q×p two-dimensional
16.24 Similar to Exercise 16.23, adapting MatMultCREW to the EREW PRAM can be done by
first broadcasting the matrix A throughout a p×q×r three-dimensional array AA (so that