Algorithms: Sequential, Parallel and Distributed 1-1
Chapter 14
Matching and Network Flow Algorithms
At a Glance
Table of Contents
• Overview
• Objectives
• Instructor Notes
• Solutions to Selected Exercises
Algorithms: Sequential, Parallel and Distributed 1-2
Lecture Notes
Overview
In this chapter we discuss two fundamental problems related to graphs and networks, the
matching problem and the flow problem. We begin this chapter with a discussion of the
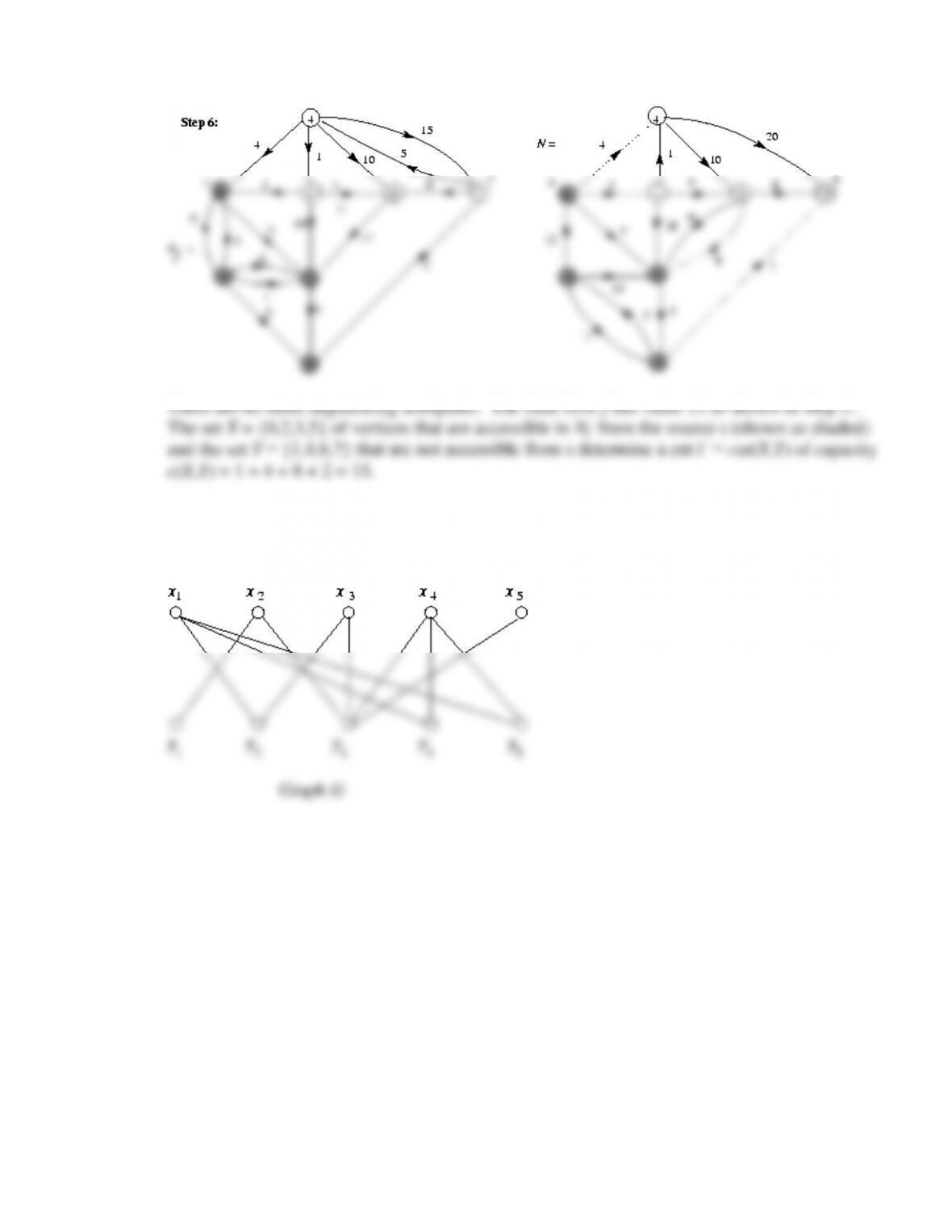
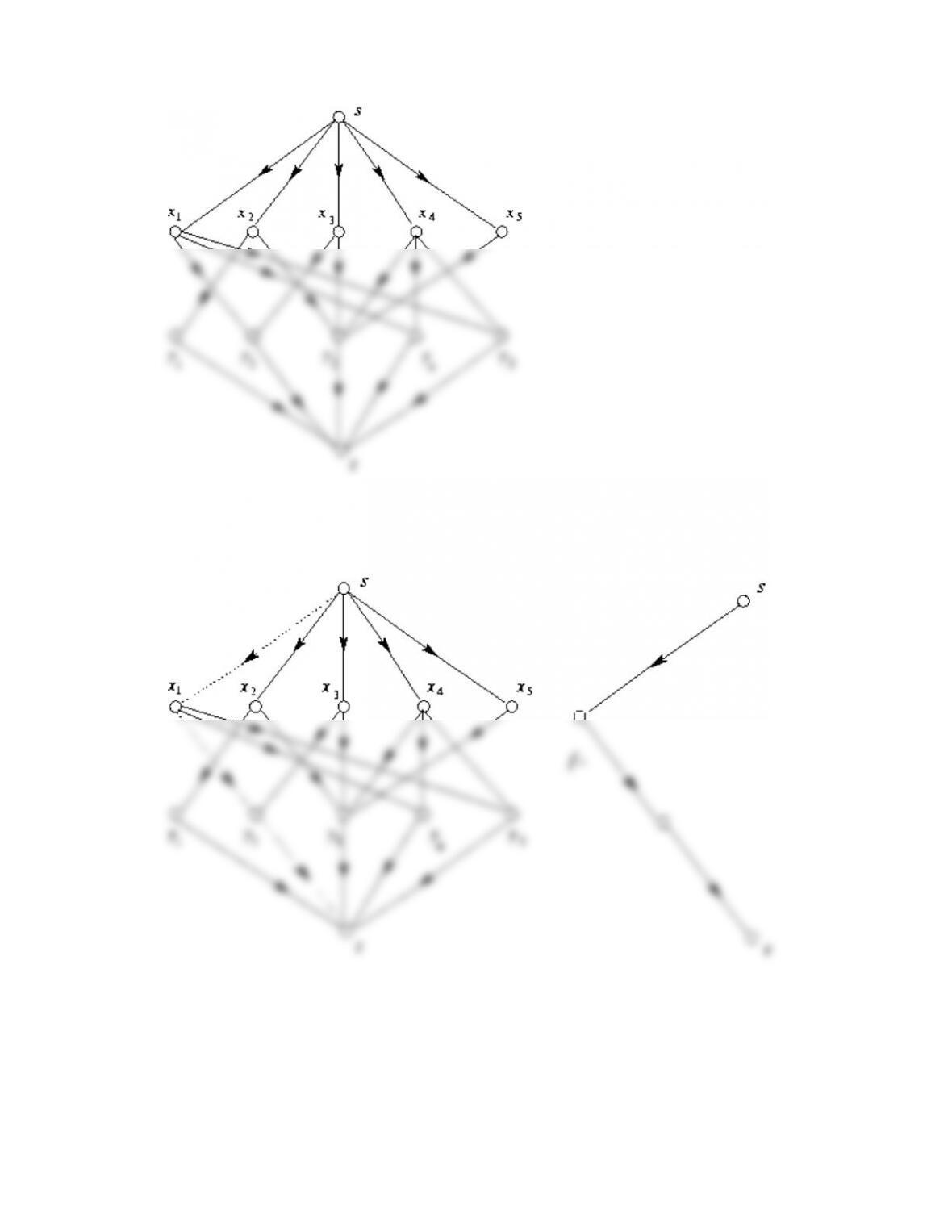
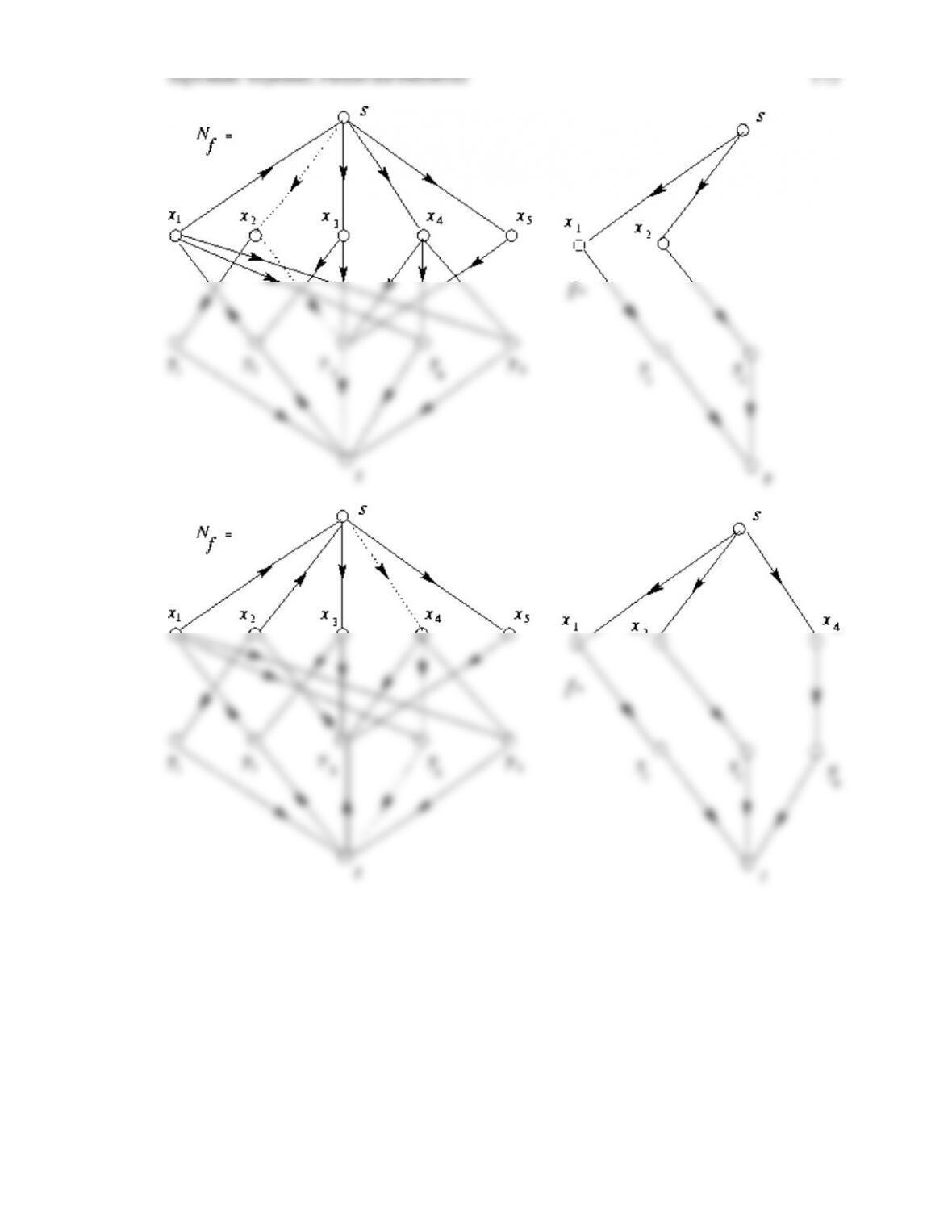
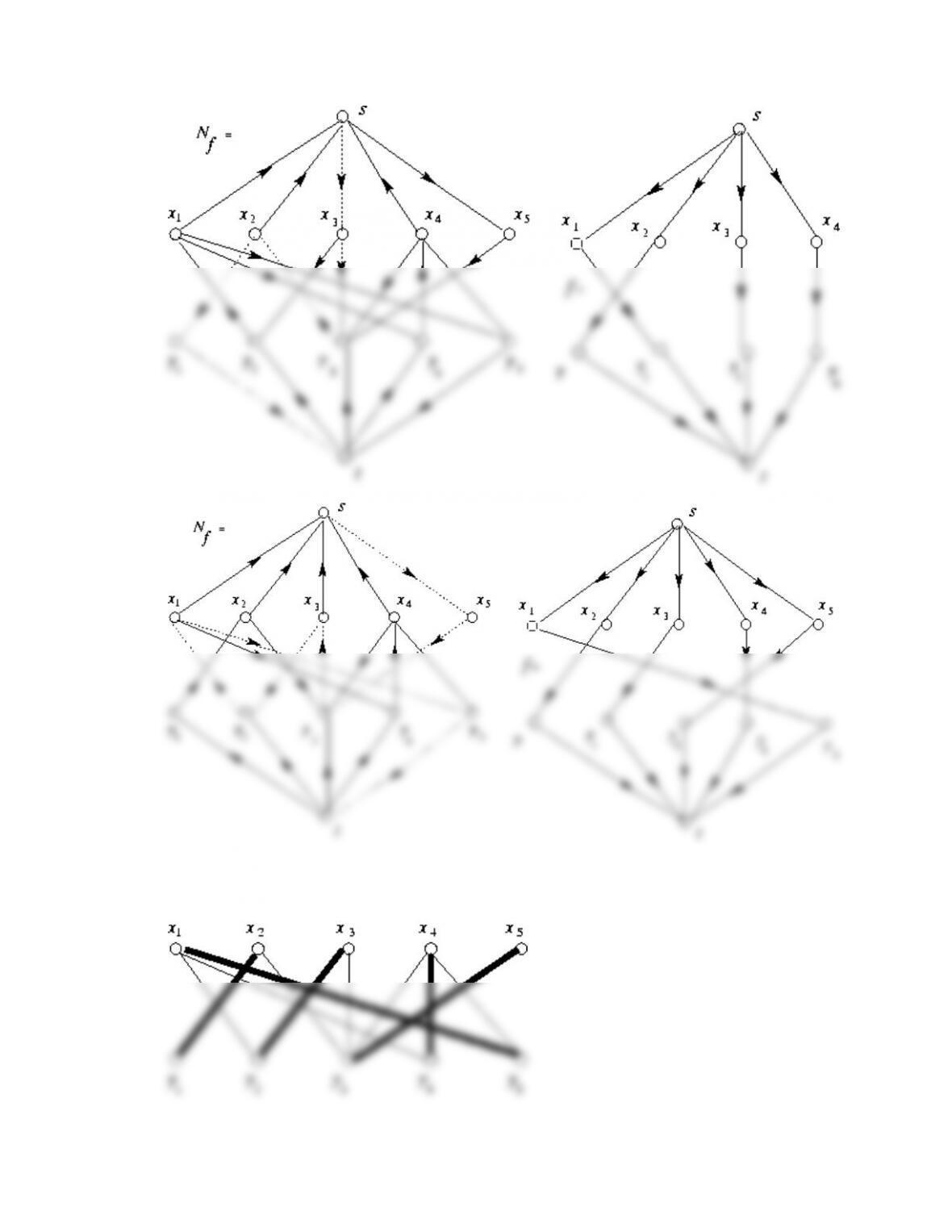
classical Hungarian algorithm for finding a perfect matching in a bipartite graph and
prove Hall’s classical theorem about the existence of a perfect matching in a bipartite
graph. We then discuss the Kuhn-Munkres algorithm, which utilizes the Hungarian
algorithm to compute a maximum weighted perfect matching in a weighted bipartite
Chapter Objectives
After completing the chapter the student will know:
• The basic definitions, such as matching, perfect matching, flow, cut, semipath,
augmenting semipath, etc.
• The Hungarian algorithm for computing a perfect matching in a bipartite graph
• The Kuhn-Munkres algorithm for computing a maximum weighted perfect
matching in a weighted complete bipartite graph.
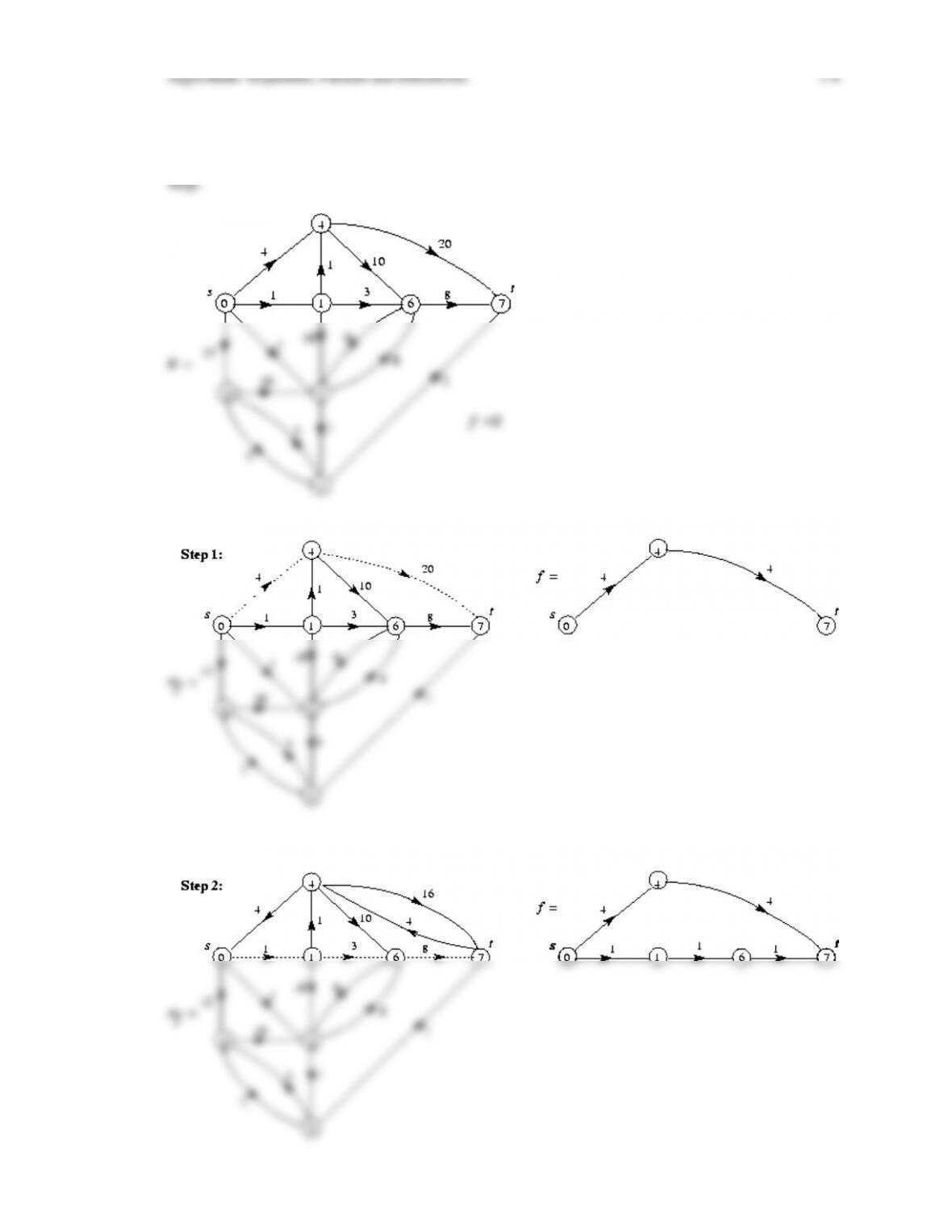
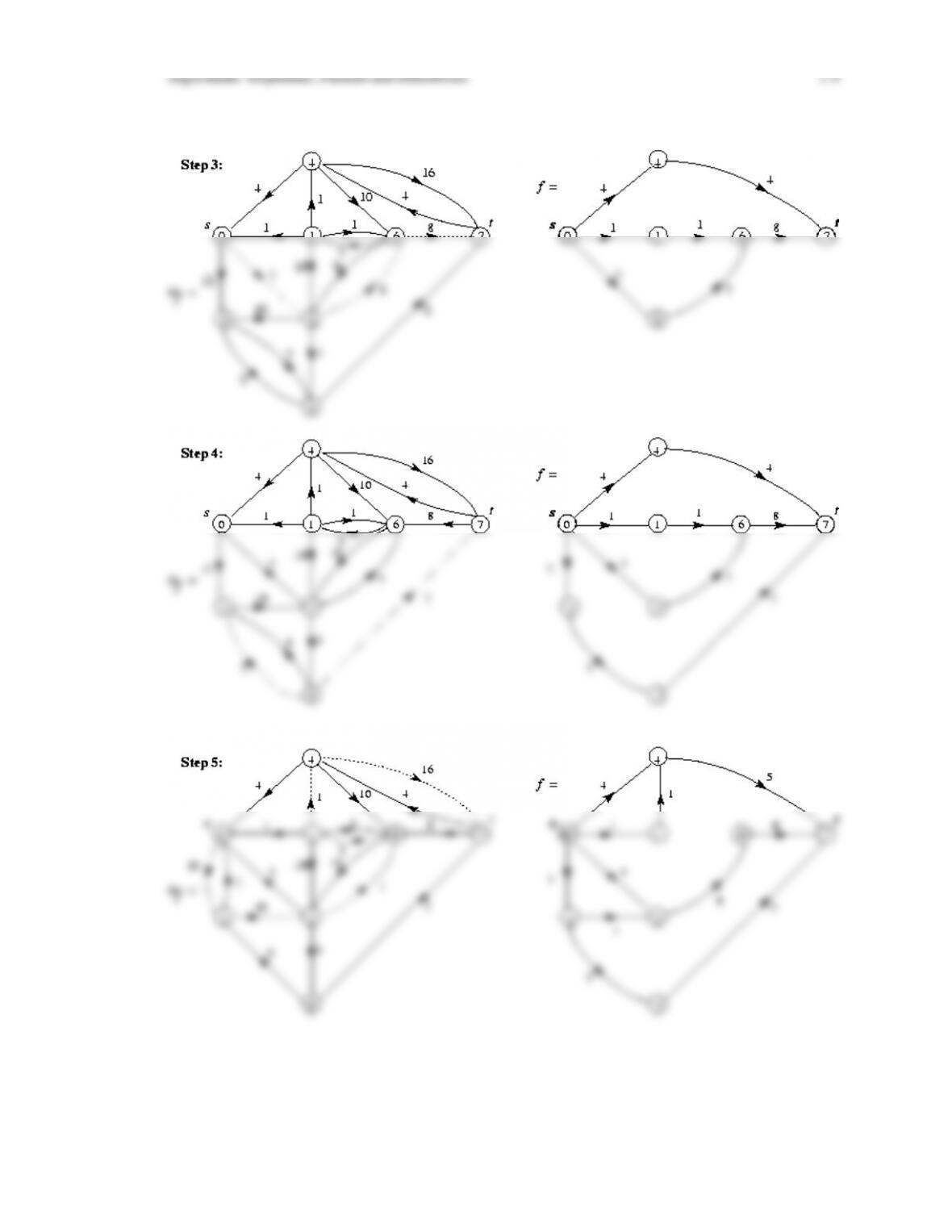
• The Max-Flow Min-Cut theorem
Instructor Notes
The instructor may wish to point out that the technique of using augmenting paths that was
applied in the Hungarian algorithm for finding a perfect matching in a bipartite graph motivates
edges to M, but also by removing some edges. Similarly, augmenting semipaths with respect to
a flow f in a capacitated network are used to increase the value of f by not only increasing the
flow on edges, but also by reducing the flow on some edges. In fact, via the construction given
in Figure 14.10 the concept of an augmenting semipath in a capacitated network with respect to
a flow generalizes that of an augmenting path in a bipartite graph with respect to a matching: an
the G has no perfect matching.
Solutions to Selected Exercises
Section 14.1 Perfect Matchings in Bipartite Graphs
14. 1 Let e1 e2 … e2k+1 denote the edges of the path P in the order they are visited when P is
traversed from initial to terminal vertex, so that the k edges e2 e4 … e2k are the edges of M.
14. 2 Since each edge of M is incident with exactly one vertex in XT, it follows that |XT| = |M|.
14. 3 Clearly, the path from the root of T to a node x
|XT| is an alternating path. Thus, the
14. 5 The M-alternating tree T can be computed using an algorithm similar to breadth-first
search rooted at r, except that, whenever a vertex x
XT, is reached the matching edge xy at x
14.6 We give two solutions generated by the procedure Hungarian. In the first solution, as in
the example on p. 424 in the text, the phrase “any … vertex” occurring in three statements in
the pseudocode for Hungarian is replaced by the phrase “the … vertex of smallest index” when
generating a perfect matching. In the second solution, we use the replacement phrase “the …
Initial matching {x1, y1}, { x3, y3}
First Solution
First M-augmenting Augmented matching M
E(P) = { x1y2, x2y1, x3y3}
path P
Second M-augmenting Augmented matching M
E(P) = { x1y2, x2y1, x3y3, x4y4}
path P
Algorithms: Sequential, Parallel and Distributed 1-5
Third M-augmenting path P
Final perfect matching M
E(P) = { x1y5, x2y1, x3y2, x4y4, x5y3 }
Second Solution
First M-augmenting path P Augmented matching M
E(P) = { x1y1, x3y3, x5y4}
Second M-augmenting path P Augmenting matching M
E(P) = { x1y1, x3y2, x4y3, x5y4}
Algorithms: Sequential, Parallel and Distributed 1-6
Third M-augmenting path P
Final perfect matching M
E(P) = { x1y5, x2y1, x3y2, x4y3, x5y4 }
14. 7 Consider any perfect matching M and let x1y1, x2y2, …, xnyn denote the edges M. Since
= =+== VvYyXx
iii vyxyxM )()()()()( 1
14. 8 Consider any edge xy. Then we have that
14. 9
Section 14.2 Maximum Flows in Capacitated Networks
14.11 Since f is a flow from s to t, for each vertex v different from s and t we have that
),()()(),( vfvwfuvfvf out
VvwEuv
in
===
. Thus, we have that
.0),(),(
},\{ =−
tsVv inout vfvf
(1)
out
14. 12
),()( 22112211 sffffval out
+=+
Esv Esv
14. 13 For v at vertex different from either s or t we have that
1),(),( == vv SinSout
, if
one edge of S is directed into to v and one edge of S is directed out of v. Otherwise, we have
that
0),(),( == vv SinSout
. Further,
.1),()( == sval SoutS
This proves that
S
is a flow.
14.15 Suppose to the contrary that there exists an edge e = xy of the cut Γ = cut(X,Y) was not
saturated. Then, f(xy) < c(xy). Thus, f(xy) – c(xy) > 0, so that xy is an edge in the f-derived
14.16 Suppose to the contrary that there exists an edge e = yx of the cut Γ = cut(X,Y), where x
and y belong to X and Y, respectively, such that f(yx) > 0. Then, f(xy) < c(xy). Then, xy is
14.19 In the following steps of the Edmonds-Karp algorithm, each shortest path chosen in the
f-derived network Nf is indicated by dotted edges. The corresponding f-derived network Nf
resulting from adding the flow associated with this path to the current flow is shown in the next
Algorithms: Sequential, Parallel and Distributed 1-10
14.22 In the following figures, all edges have unit capacity, and the flow value on any edge at
any given step is either 0 or 1.
Algorithms: Sequential, Parallel and Distributed 1-11
Associated network N, with each edge having unit capacity
Algorithms: Sequential, Parallel and Distributed 1-13
The Edmonds-Karp algorithm now terminates with the following maximum matching of the
orginial graph G having been found, which in this case is a perfect matching.
14.23 Consider the transformation of a bipartite graph G to a digraph D as illustrated in Figure
14.10. It is easily verified that a maximum set of pair-wise edge-disjoint paths in D from s to t