The problems in this chapter are primarily mathematical. They are intended to give students
some practice with the concepts introduced in Chapter 2, but the problems in themselves offer
few economic insights. Consequently, no commentary is provided. Results from some of the
analytical problems are used in later chapters, however, and in those cases the student will be
directed back to this chapter.
Solutions
2.1
22
( , ) 4 3 .f x y x y
6 2 3
dx
d. The
( , ) 16f x y
contour line is an ellipse centered at the origin. The slope of the
line at any point is given by
8 6 .dy dx x y
Notice that this slope becomes
more negative as x increases and y decreases.
2.2 a. Profits are given by
2
2 40 100.R C q q
The maximum value is found
by setting the derivative equal to 0:
4 40 0
d = q +
dq
,
implies
*10q
and
*100.
CHAPTER 2:
Mathematics for Microeconomics
( , ) 16f x y
2.4 Setting up the Lagrangian,
(0.25 ).x y xy
L
The first-order conditions are
1,
x
y
L
*40 .tg
b. Substituting for
*,t
2
*40 40 800
*
2
( ) 800.
df t
dg g
Chapter 2: Mathematics for Microeconomics
2
*
.MC
By the fundamental theorem of calculus,
0
( ) ( ) (0),
q
MC x dx TC q TC
*
180.5 98
82.5.
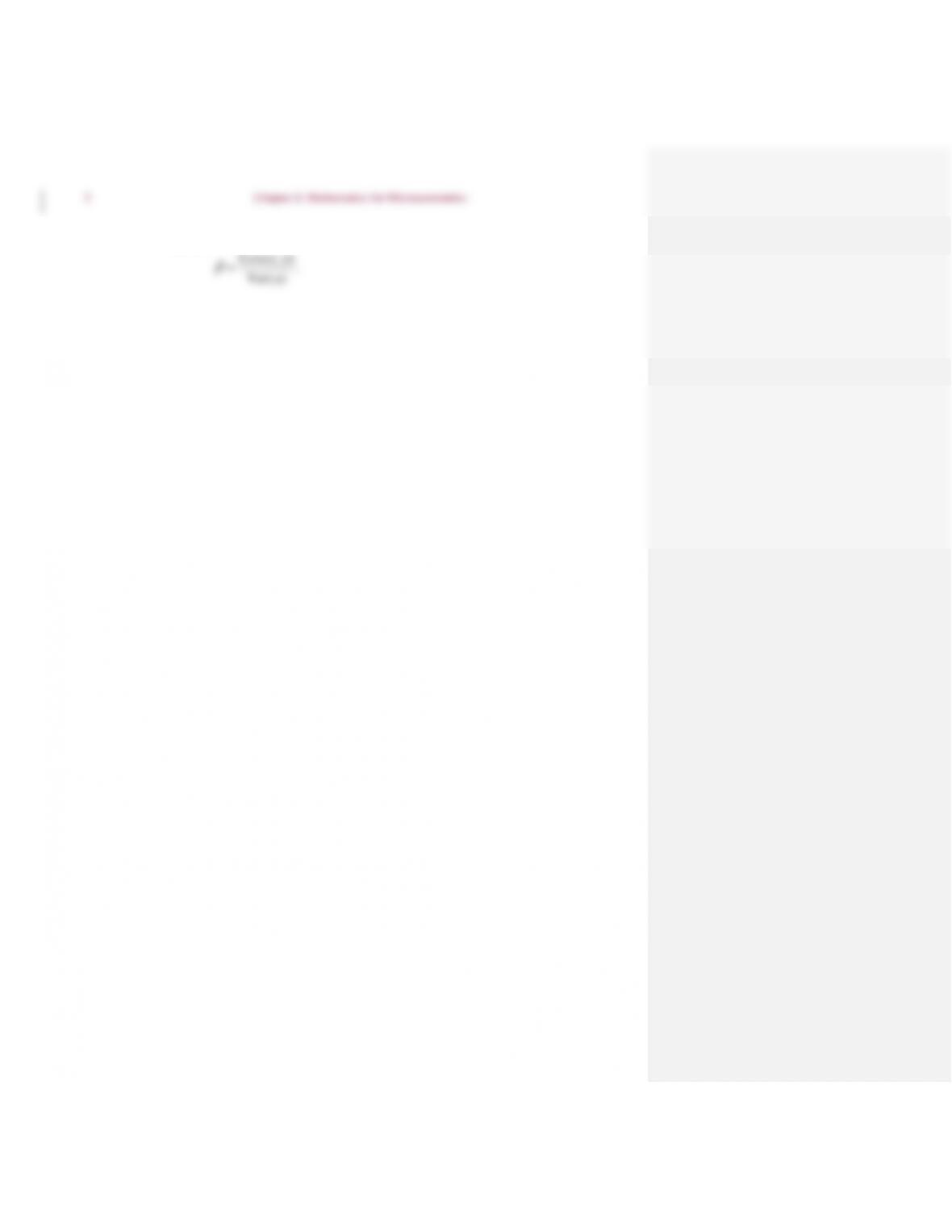
d. Assuming profit maximization, we have
2
2
( ) ( )
( 1)
( 1) ( 1) 98
2
( 1) 98.
2
p pq TC q
p
p p p
p
e. i. Using the above equation,
( 20) ( 15) 82.5 0 82.5.pp
ii. The envelope theorem states that
*( ).d dp q p
That is, the derivative of
the profit function yields this firm’s supply function. Integrating over
p
shows
the change in profits by the fundamental theorem of calculus:
20
15
20
15
20
2
15
(20) (15)
( 1)
2
180 97.5
82.5.
p
p
ddp
dp
p dp
pp
Analytical Problems
2.9 Concave and quasi-concave functions
The proof is most easily accomplished through the use of the matrix algebra of quadratic forms.
See, for example, Mas Colell et al.,1995, pp. 937–939. Intuitively, because concave functions lie
below any tangent plane, their level curves must also be convex. But the converse is not true.
Quasi-concave functions may exhibit “increasing returns to scale”; even though their level
curves are convex, they may rise above the tangent plane when all variables are increased
together.
Chapter 2: Mathematics for Microeconomics
2
A counter example would be the Cobb–Douglas function, which is always quasi–
concave, but convex when
1.
2.10 The Cobb–Douglas function
a.
1
2 1 2
2
11 1 1
2
22 1 2
11
12 21
1
12
0,
( 1) 0,
( 1) 0,
0.
0,
f x x
f x x
fx
x
x
f
fx
x
fx
Clearly, all the terms in Equation 2.114 are negative.
b. A contour line is found by setting the function equal to a constant:
12
,y c x x
implying
1
21
.x c x
Hence,
2
1
0.
dx
dx
2.11 The power function
is concave. Because
12
, 0,ff
Equation 2.114 is also satisfied, so the function is
quasi-concave.
c.
y
is quasi-concave as is
.y
However,
y
is not concave for
1.
This can be
shown most easily by
1 2 1 2
(2 ,2 ) 2 ( , ).f x x f x x
2.12 Proof of envelope theorem
Formatted: Indent: Left: 0″, First line: 0″
Chapter 2: Mathematics for Microeconomics
2
a. The Lagrangian for this problem is
b., c. Multiplication of each first-order condition by the appropriate deriviative yields
2211
1 2 1 2 0.
dx dx dx dx
f f g g
da da da da
*12
12 .
a
da
dx dx
d
df f f f
da a
e. Differentiation of the constraint
12
( ), ( ), 0g x a x a a
yields
1
2
dx dx
dg g g g
*.
a a a
df fg
da
L
Lagrangian shows also that
*.
dA
dP
This shows that the Lagrange multiplier does indeed show this incremental gain in
this problem.
2.13 Taylor approximations
a. A function in one variable is concave if
( ) 0.fx
Using the quadratic Taylor
1
11
x
4. To show Markov’s inequality use
21 ()
Ex
f. 1. Show that the PDF integrates to 1:
2
223
11
81
1.
3 9 9 9
x
x
xx
dx
2
234
11
15 5
( ) .
3 12 12 4
x
x
xx
E x dx
( 1 0Px
):
0
023
11
1.
3 9 9
x
x
xx
dx
Chapter 2: Mathematics for Microeconomics
2
2
22
2 2 2
22
Var( ) ( )
2 ( ) [ ( )]
()
.
2[ ( )] [ ( )]
( ) [ ( )]
x E x E x
E x xE x E x
E x E x E x
E x E x
b. Here, we let
x
yx
and apply Markov’s inequality to
y
and remember that
x
can only take on positive values.
2
2
22
22
()
( ) ( ) .
x
Ey
P y k P y k kk
independent.
