Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
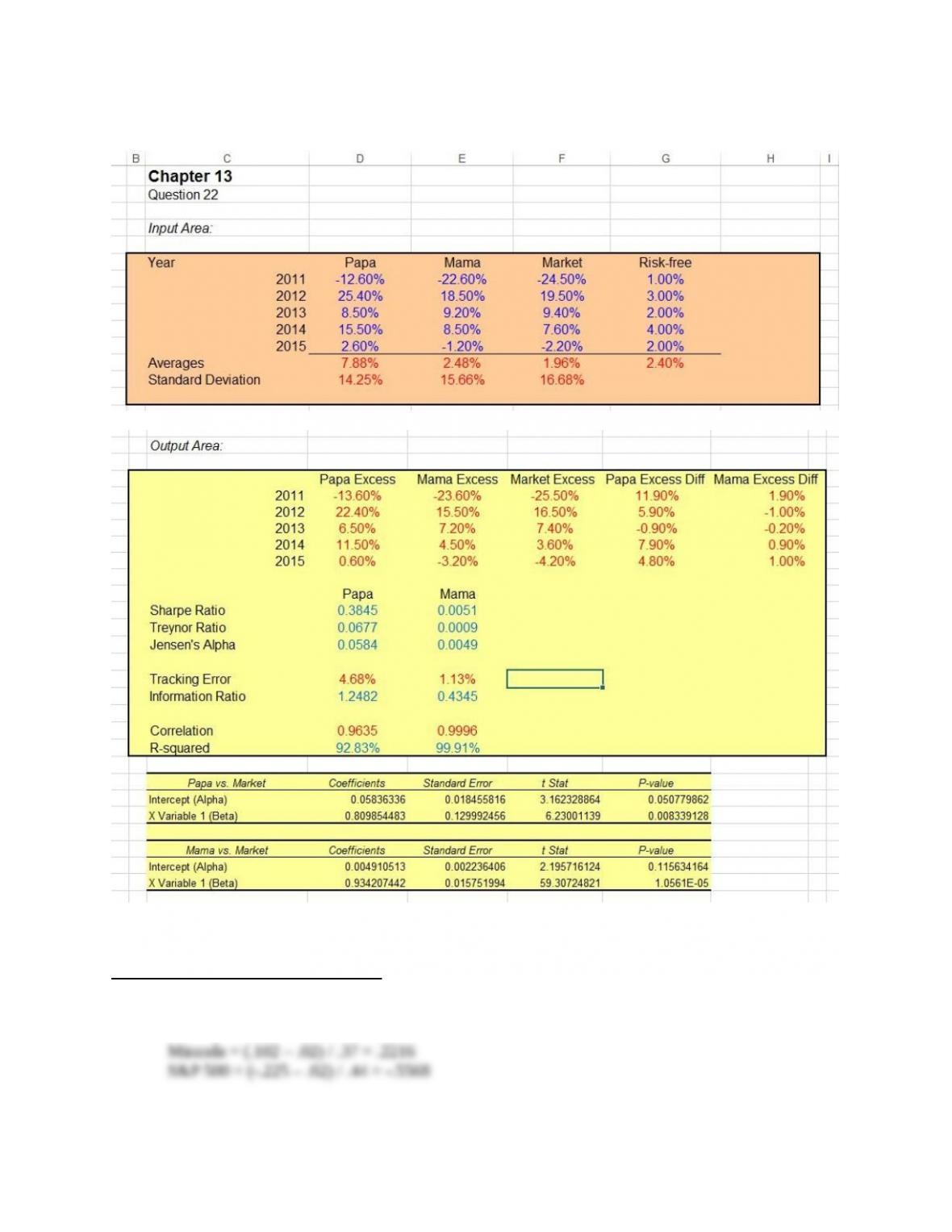
Chapter 13
Performance Evaluation and Risk Management
Concept Questions
1. The Sharpe ratio is calculated as a portfolio’s risk premium, or excess return, divided by the standard
2. A common weakness of both the Jensen alpha and the Treynor ratio is that both require an estimate
3. Jensen’s alpha is the difference between a stock’s or a portfolio’s actual return and that which is
4. An advantage of the Sharpe ratio is that a beta estimate is not required; however, the Sharpe ratio is
5. To determine significance, one might use the t-statistics or p-values from a regression estimate.
6. A Sharpe optimal portfolio is the portfolio with the highest possible Sharpe ratio given the available
7. The Sharpe ratio uses total deviation from the mean, while the Sortino ratio uses only returns that are
8. After establishing the desired probability (x), the VaR statistic provides the minimum loss you would
10. For sector funds or investments that only cover a portion of the market (e.g., value or growth), a
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
Solutions to Questions and Problems
NOTE: All end of chapter problems were solved using a spreadsheet. Many problems require multiple
steps. Due to space and readability constraints, when these intermediate steps are included in this
solutions manual, rounding may appear to have occurred. However, the final answer for each problem is
found without rounding during any step in the problem.
Core Questions
2 / 12
2. 8.60% /
√
1 / 12
= 29.79%
3.
Portfolio Sharpe ratio Treynor ratio Jensen's alpha
X .27586 .0640 .50%
5. R-squared gives the percentage of the fund’s return driven by the market, which is:
9. E(R) = (.12 + .18) / 2 = .15
10. For a portfolio with two investments having zero correlation, the Sharpe ratio would be calculated as
follows:
Sharpe ratio =xSE(RS)+ xBE(RB) - Rf
(xS
2σS
2+ xB
2σB
2)1/2
11.
Sharpe ratio =.5E(RS)+.5E(RB) - Rf
[. 52σS
2+.52σB
2+. 2(.5 )(.5 )(σS)(σB)(Corr (RS,RB))]1/2
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
12. Any portfolio of the two securities will also have the same expected return.
Sharpe ratio =E(RS) - Rf
(xS
2σS
2+ xB
2σB
2)1/2 =E(RB) - R f
(xS
2σS
2+ xB
2σB
2)1/2
13. Prob(R .11 – 2.326(.54)) = 1%
14. Prob(R .11 + 2.326(.54)) = 1%
15. E(R) = (.10 + .18) / 2 = .1400
16. E(R) = (.10 + .18) / 2 = .1400
17. E(R) = .14
18. wA = [(.12 – .05)(.482) – (.15 – .05)(.29)(.48)(.25)] / {(.12 – .05)(.482) + (.15 – .05)(.292)
– (.12 – .05 + .15 – .05)[(.29)(.48)(.25)]}
19. Sharpe = (.0546 - .0240) / .1505 = .2034
20. First find the average returns of the fund, the market and the risk free rate, which are 5.46%, 1.96%,
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
2.40%, respectively. The deviations for the fund and the market returns are 15.05% and 16.68%,
respectively.
Next find the excess return over the risk free rate, as well as the difference between the fund and
market returns.
Fund Excess Market Excess Difference
2011 -16.20% -25.50% 9.30%
The correlation between the fund and the market is .97.
The tracking error is the standard deviation of the difference in returns, which is 4.14.
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
Spreadsheet Problem
21. The Solver inputs are:
based on the following spreadsheet.
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
22.
CFA Exam Review by Kaplan Schweser
1. a
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
2. c
3. b
Copyright © 2018 McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill
Education.
