Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
Nonlinear equations 199
325 %this is a vapor
326 P = vdw(V,T,a,b);
327 else
328 %this is on the horizontal part
339 ylabel('$P$ (MPa)','FontSize',14)
340 top = strcat('Isotherm for $T = $',num2str(T),'K');
341 title(top,'FontSize',14)
342 out = h;
343
351 %vdW parameters: a,b
352 %units: P = MPa, V = L/mol, T = K
353
354 Pplot = zeros(500,1);
355 Vlplot = Pplot;
366 Vlplot(2) = Vl;
367 Vgplot(2) = Vg;
368 Tplot(2) = T;
369
370 fprintf('Go down from 395 K to 365K in -1 K increments')
380
381 fprintf('Go up to critical point in +1 K increments')
382 %now go up to 438 K from the value at 395 K. Reinitialize guesses
383 T = 395; Psat = Pplot(2); Vl = Vlplot(2); Vg = Vgplot(2);
384 for i = 33:75
395 for i = 76:125
396 T = T+0.1;
397 [Vl,Vg,Psat] = equilibrium(Psat,T,Vl,Vg,a,b);
398 Pplot(i) = Psat;
399 Vlplot(i) = Vl;
410 Vlplot(i) = Vl;
411 Vgplot(i) = Vg;
412 Tplot(i) = T;
413 end
414
425
426 %make the PV plot
427 g=figure;
428 plot(Vlplot,Pplot,'ob',Vgplot,Pplot,'ob')
429 xlabel('$\underline{V}$ (L/mol)','FontSize',14)
439 xlabel('$T$ (K)','FontSize',14)
440 ylabel('$P$ (MPa)','FontSize',14)
441 title('Phase envelope','FontSize',14)
442 text(370,1.8,'Liquid')
443 text(420,1,'Vapor')
(a) You want to rewrite the van der Waals equation of state in the form f(V) =0,
In Newton’s method, you need the derivative too,
A decent guess is 0.5, and the solution converged to a molar volume of 0.507813
L/mol.
The file output for this part is:
0.5 1 1.5 2 2.5 3
0
1
2
3
4
5
6
V(L/m ol)
P(MPa)
vdw Equat ion for T=470K
(b) Starting the volume very close to bwill usually converge to the root for the
liquid. Looking at the isotherm, you can see that the liquid root is around 0.4.
You can see that Newton’s method converged to the liquid’s root. The calculation
0.5 1 1.5 2 2.5 3
0
1
2
3
4
5
6
V(L/m ol)
P(MPa)
vdw Equat ion for T=425K
0 1 2 3 4 5 6 7 8 9 10
0.2
0.25
0.3
0.35
0.4
0.45
New t on method iterat ion, k
Value of molar volume, Vk(L/mol)
Evolution of Ne w ton Method f or V( 0 ) =0.23
10−14
10−12
10−10
10−8
10−6
10−4
10−2
100
102
Newton me tho d it e ration, k
Err or , |f(Vk|
Evolution of Ne w t on Method f or V( 0 ) =0.23
C o m p u t e d E rr or
S c a l in g R e s u l t
Nonlinear equations 203
(c) This calculation fails massively. If I print out the first 18 iterations, I can see
what happened:
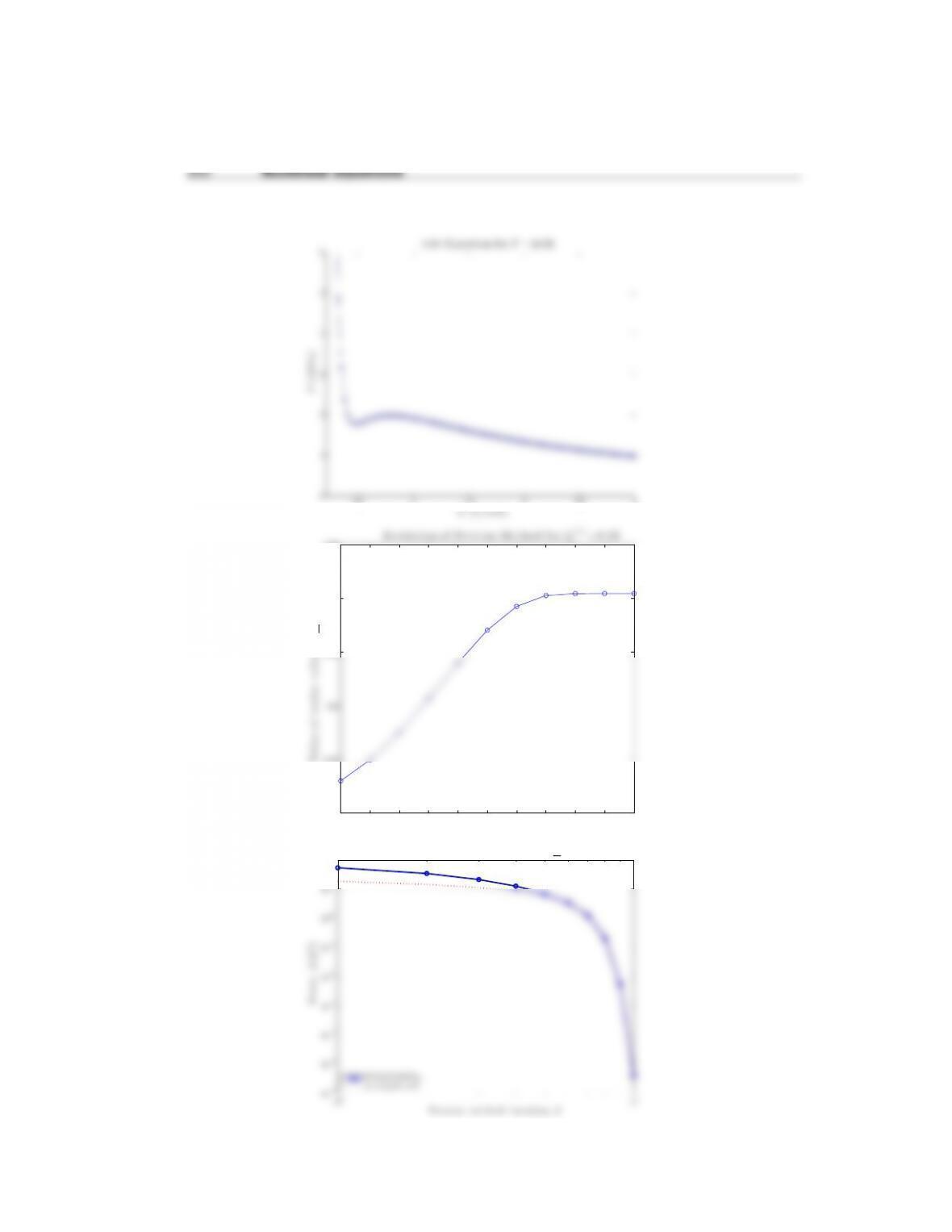
Computing volume for Vinit = 0.600000000
k V err
1 0.704145230 -3.335338e-02
3 1.804569869 -5.655852e-01
5 0.803762387 -1.738042e-02
7 0.696989028 -3.650306e-02
9 1.122542959 -1.538455e-01
11 0.768445361 -1.765214e-02
13 0.832381352 -2.070888e-02
15 0.787732853 -1.685907e-02
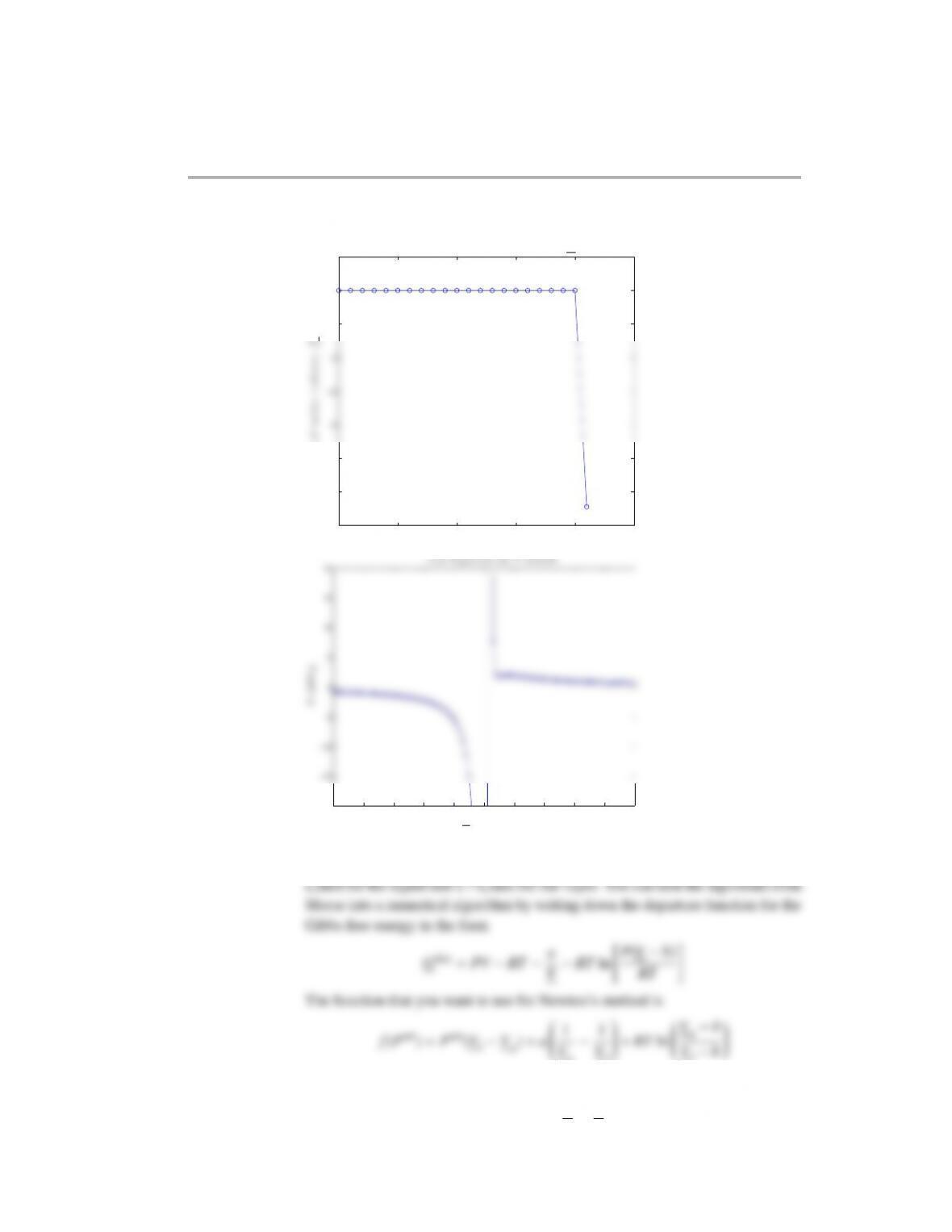
The calculation fails at iteration 21 because there is an overflow error. The plot of
point. The roots all converge at the critical temperature, so it becomes extremely
difficult to find the volume because the roots and the critical points of the function
are all very close. It is easy to hit the critical point of the function and get sent to
an unphysical, unrecoverable solution.
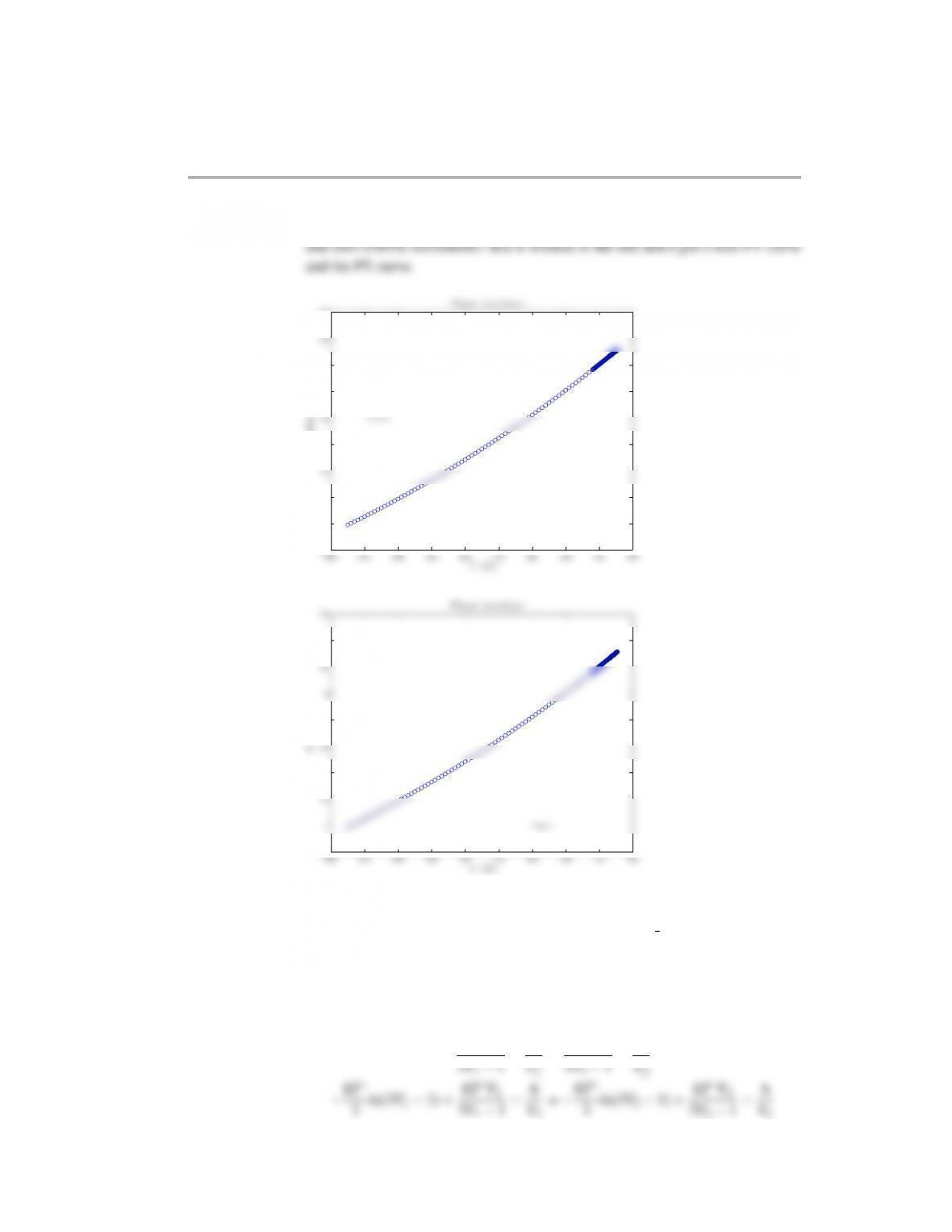
The file outputs for this part are:
204 Nonlinear equations
0 5 10 15 20 25
−14
−12
−10
−8
−6
−4
−2
0
2
x 1058
New t on method iterat ion, k
Value of molar volume, Vk(L/mol)
Evolution of Ne w ton Method f or V( 0 ) =0.6
−5 −4 −3 −2 −1 0 1 2 3 4 5
−20
−15
−10
−5
0
5
10
15
20
V(L/mol)
P(MPa)
vdw Eq uation f or T=425K
(d) The outputs for this part has a plot of the isotherm and a guess of 1.3 MPa
for the saturation pressure. At that pressure, a good guess for the volumes is 0.4
Vg−1
Vl
Vl−b
which has a very simple derivative,
f′(Psat)=Vl−Vg
Nonlinear equations 205
Note that you are working in somewhat strange units, but a MPa L/mol is actually
a kJ/mol. At each iteration, you want to first update Psat by Newton’s method,
k)
1.404886 MPa, Vl=0.352873 L/mol, and Vg=1.522065 L/mol. The plot of the
isotherm and the original cubic equation is provided.
0.5 1 1.5 2 2.5 3
0
0.5
1
1.5
2
2.5
3
V(L/mol)
P(MPa)
Guess of Psat for T=395K
2
3
4
5
6
P(MPa)
I s ot he r m f or T=395K
E O S v al u e s
I s ot h e r m
to 0.1K increments. To get really close to the critical point, I had to go to 0.01 K
206 Nonlinear equations
(4.1) The equations required for implicit Euler are
y1,i+1=y1,i−hky1,i+1y2
2,i+1
y2,i+1=y2,i−2hky1,i+1y2
2,i+1
y=0.9596. From the forward Euler, we have
yi+1=1+(0.01)(22−23)=0.96
0.1 0.5583 0.6 0.5149
1 -8.9167 -3 -17
(4.3) For one step of the predictor corrector with h=0.01 we get a predictor
yp
1=10 +0.01[cos(π)−102sin(π)] =9.99
(4.4) We first compute all of the kvalues:
k1=ln(2) =0.693
(4.5) Explicit Euler is
yn+1=yn+h f (yn)
and predictor-corrector is
In order for the values of yn+1to be the same, we need
Simplifying gives
The simplest way for this to be true is if f(yn)=0, i.e. if the derivative is zero at this
point and the function is flat. It is also possible to have a function f(y) where the step
size is such that the current value and the explicit Euler value with a step size hgive
the same slope, such as a periodic function.
(4.6) The predictor-correction solution is
y1=yp
2=3+17/4
2=12 +17
8=29
8
The error in the solution with h=1/4 is |4−29/8|=3/8. Since the error in this
scheme is quadratic, we would expect that
Initial value problems 223
Solving for h, we get
(4.7) (a)
(b) Implicit Euler requires newtons method or something similar to solve for yi+1
First put it in the form of a residual
then differentiate with respect to yi+1
xis the independent variable so it is known. Newton’s method for the kth iteration
is:
i+1−yi−h(y2(k)
i+1exp(−2xi+1))
The converged result is the new value of yi+1
(c) Predictor-corrector starts with an explicit euler step
After is a second step using yp
i+1
the new value of yi+1is the average of the two values
yi+1=yp
i+1+yc
i+1
2
(4.8) (a)
224 Initial value problems
(c) The equation for Implicit Euler is
this equation must be solved for yi+1. One simple way to do this is Newtons
method. The value of xi+1is known so first we write the above equation in the
form of a residual.
i+1,xi+1)
The converged result of Newtons method is now the new value of yi+1
(4.9) (a) Explicit Euler requires 5 time steps to evaluate y(2.5) the first is:
(4.10) The script to used to generate the solution to this problem can be found in 92p6p34 matlab.
The Matlab program for this problem is
Initial value problems 225
1function f92p6p34
2clc
3close all
4%initialize time steps
15 yee(2,1)=6;
16 for i=2:npts+1 %loop for EE
17 rke=getk(yee(:,i-1));
18 yee(:,i)=yee(:,i-1)+h*rke;
19 tee(i)=tee(i-1)+h;
integration\n')
30 disp(c) %displays the values for the initial condition and the ...
time steps required
31
32 %initilization for RK4
43 rk3=getk(yrk(:,i-1)+(h/2)*rk2);
44 rk4=getk(yrk(:,i-1)+h*rk3);
45 yrk(:,i)= yrk(:,i-1)+(h/6)*(rk1+2*rk2+2*rk3+rk4);
46 trk(i)=trk(i-1)+h;
47 end
56 rk=[trk;yrk];
57 for i=1:3
58 str1=L(i,:);
59 str2=num2str(rk(i,:));
60 d(i,:)=[str1,str2];
70 out(1,1)=dy1;
71 out(2,1)=dy2;
(a) Explicit Euler requires 4 time steps to reach t=2. The values of the intermediate
steps are
(b) For RK4 only one time step is needed but 4 function evaluations are computed
the four K vectors (listed y1;y2) are
(4.11) (a) Explicit Euler requires 4 steps to reach y(1) the first is:
The next four are
Initial value problems 227
(b) RK4 takes only one time step but requires four function evaluations. They are:
The final value is y(1) ≈0.8203
(4.12) (a) What differential equation is solved by this program?
(e) What does the variable crepresent?
The derivative of the residual (or function) for Newton’s method. It also OK if
they just write the equation that we are describing:
(4.13) The local stability analysis is
∂f
(4.14) (a) Rewriting the equations in matrix form:
d
dt "y1
y2#="0 1
−2−3#" y1
y2#
The constant matrix has eigenvalues with corresponding vectors:
Initial value problems 229
(d) The stability criteria for explicit euler is hλ≤2. The value of the eigenvalue
(4.15) Convert these into a system of equations by defining y1=yand y2=y′
The eigenvalue equation is λ2+4y2λ−1=0. Using the quadratic equation, the
eigenvalues are λ=−2y2±q4y2
2+1. The discriminant is always positive, so the
eigenvalues are real. For forward Euler to be stable, we require h≤2/|λmax|. The
maximum eigenvalue depends on the sign of the slope of the function:
−2y′−p(2y′)2+1 (y′>0)
(4.16) First we must compute the Jacobian in order to find the eigenvalues of problem about
Now we evaluate the Jacobian at t=0 such that (y1,y2)=(.5,5)
The eigenvalues of this matrix are λ=−3.618 and λ=−1.382. The stability criteria
230 Initial value problems
for explicit euler is hλ≤2. The value of the eigenvalue used is the absolute value of
the largest eigenvalue thus:
Based on the values of the eigenvalues returned for this matrix about t=0 I would
not expect this system to be stiff.
(4.17) This problem is the forward Euler integration of the differential equation
For non-linear ODEs, the approximation for the eigenvalue at some point ysis
In this problem, the time step of 0.05 is definitely smaller than the max step size.
(4.18) You need 4 coupled equations. The explanation is not required, but the problem you
need to solve is:
(4.19) Let the subscript on ydenote the order of the derivative. For the first equation, we get
d
y0
y1
=
y1
y2
,
y0
y1
=
2
1
y3
y0
y3
0
