Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
Solutions to Chapter 5 Exercises
SOLVED EXERCISES
S1. (a) R’s best-response rule is given by y = 10√x – x. L spends $16 million, so x = 16. Then
(b) R’s best response is y = 10√x – x, and L’s best response is x = 10√y – y. Solve these
simultaneously:
x = 10(10√x – x)1/2 – 10√x + x
S2. (a) Xavier’s costs have not changed, nor have the demand functions, so Xavier’s
(b) See the graph below. Yvonne’s best-response curve has shifted down; it has the same
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
S3. (a) La Boulangerie’s profit is
To find the optimal P1 without using calculus, we refer to the result in the appendix to Chapter 5,
This is La Boulangerie’s best-response function. You get the same answer by setting
1 1
/Y P¶ ¶
= –2P1 + 15
– 0.5P2 = 0 and solving for P1.
Similarly, La Fromagerie’s profit is
To find the solution for the equilibrium prices analytically, substitute La Fromagerie’s
best-response function for P2 into La Boulangerie’s best-response function. This yields P1 = 7.5 –
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
(b) Colluding to set prices to maximize the sum of profits means that the firms maximize the
joint-profit function:
Solving these two equations simultaneously yields the solution P1 = 3.5 and P2 = 9.
You can get the same answer by partially differentiating the joint-profit function with respect to
2
(c) When firms choose their prices to maximize joint profit, they act as a single firm and
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
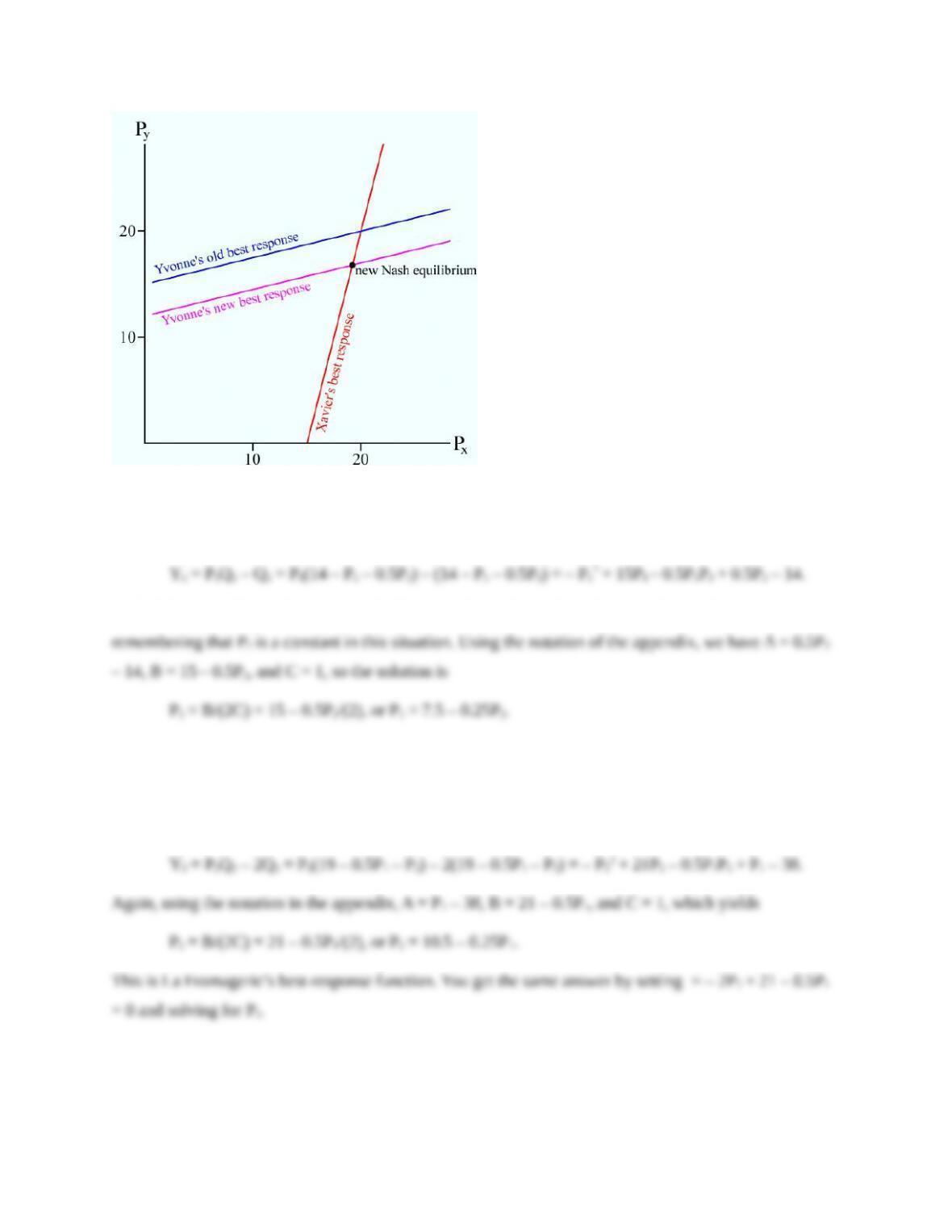
instance, plugging the joint-profit-maximizing value of La Boulangerie’s price into La Fromagerie’s
individual best-response rule will not yield La Fromagerie’s joint profit-maximizing price:
Likewise, plugging the joint-profit-maximizing value of La Boulangerie’s price into La Fromagerie’s
individual best-response rule gives
Thus, the two joint profit-maximizing prices are not best responses to each other; that is, they do not form
a Nash equilibrium.
(d) When firms produce substitutes, a drop in price at one store hurts the sales of the other.
Thus, as your rival drops her price, you also want to drop yours to attempt to maintain sales (and profits).
S4. To rationalize the nine possible outcomes, you need a separate argument for each one. We offer
just one example, leaving you to construct the rest. Note that you need not consider the strategy
S5. No matter what beliefs Colin might hold about what Rowena is playing, South is never Colin’s
best response. Therefore, South is not a rationalizable strategy for Colin. Since Rowena recognizes this,
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
S6. Using the third-round range of R, we have that S = 12 – R/2 must be at most 12 – 9/2 = 12 – 4.5
S7. (a) Cart 0 serves x customers and Cart 1 serves (1 – x), where x is defined by the equation
(b) Profits for Cart 0 are (p1 – p0 + 0.5)(p0 – 0.25). Profits for Cart 1 are symmetric:
(c) The graph is shown below. The Nash equilibrium prices are the values of p0 and p1 that
S8. (a) South Korea’s profit is
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
Using the notation in the appendix yields A = 0, B = 150 –qJapan, and C = 1, so South Korea’s best response
is
This is South Korea’s best-response function. You get the same answer by setting
Since Japan has the same price and cost per ship as South Korea, Japan’s profit is
Similarly, Japan’s best-response function is
(b) To find the solution for the equilibrium prices, substitute Japan’s best-response function
for qJapan into South Korea’s best-response function. This yields
South Korea’s profit is
Likewise, Japan’s profit is
Therefore, both countries make $2.5 billion in profits.
(c) South Korea’s new best-response function is
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
Japan’s new best-response function is
To find the solution for the new equilibrium prices, substitute Japan’s new best-response function for qJapan
into South Korea’s best-response function. This yields
Given this value for qKorea,
South Korea’s market share is 60 / (60 + 45) ≈ 57%, and Japan’s market share is approximately 43%.
South Korea’s profit is
YKorea = –qKorea2 + (180 – cKorea)qKorea – qKoreaqJapan
Japan’s profit is
YJapan = –qJapan2 + (180 – cJapan)qJapan – qKoreaqJapan
S9. (a) South Korea’s profit is
YKorea = qKorea, P – cKoreaqKorea = qKorea(180 – Q) – 30qKorea = qKorea(180 – qKorea – qJapan – qChina) – 30qKorea
Using the notation in the appendix, A = 0, B = 150 – qJapan – qChina, and C = 1, so the solution is
solving for qKorea.
Since Japan and China face the same price (P = 180 – Q) and cost (cKorea = cJapan = cChina) as South
Korea, the best-response functions for Japan and China are
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
(b) To find the solution for the equilibrium prices, first substitute China’s best-response
function into Japan’s best-response function:
Next, substitute Japan’s best-response function into China’s best-response function:
Then substitute these expressions for qJapan and qChina into South Korea’s best-response function:
Each country produces 37.5, so each has a market share of 33.3%.
Since each country has the same market share, price, and cost, they will all earn the same profit.
South Korea’s profit is
YKorea = –qKorea2 + (180 – 30)qKorea – qKorea * qJapan – qKorea * qChina
(c) In the duopoly situation, each country produced 50 VLCCs per year at a price of $80
million each, for a profit of $2.5 billion per country. In the triopoly, each country produced 37.5 VLCCs
S10. (a) Since the joint profits of the partnership are split equally, Monica and Nancy each get a
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
(b) We find Nancy’s best-response function by maximizing the expression Yn = 2m + 2n +
(c) We know from part (b) that Nancy’s best-response function is n = 1 + 0.25m. The game is
symmetric; Monica’s best-response function is m = 1 + 0.25n. To find the solution for the equilibrium
effort levels, substitute Nancy’s best-response function into Monica’s best-response function:
S11. Because Xavier cannot rationally believe that Yvonne will charge a negative price, and because
However, this narrows the range of prices only from below the Nash equilibrium. To narrow from
above, we need a starting point, namely an upper limit to the prices, such that no rational player would
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
meals, but that is because the linear functions we stipulated are unlikely to be valid over such a large
range. If it is not rational for anyone to charge a price higher than, say, 500, then because they know this,
S12. (a) The average of all numbers must be between 0 and 100. Thus the target number must be
(b) If all of Elsa’s classmates choose 40, then X = [49(40) + n]/50 = (1,960 + n)/50, where n
is the number Elsa selects. To win, Elsa’s number must be closer to one-half X than 40. Because of this,
(c) Similarly, if Elsa knew that all of her classmates would submit the number 10, then X =
[49(10) + n]/50 = (490 + n)/50. For Elsa to win, her number must be closer to one-half X than 10. Again,
(d) At a symmetric Nash equilibrium, all students will be choosing the same number. From
(e) To find rationalizable strategies to this game, use iterated elimination of
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
