Unlock document.
This document is partially blurred.
Unlock all pages and 1 million more documents.
Get Access
Solutions to Chapter 12 Exercises
SOLVED EXERCISES
S1. (a) The payoff table for the two types of travelers follows:
High Low
(b) The graph is shown below:
(c) There are three possible equilibria: a stable monomorphic equilibrium of all Low types (h
S2. Throughout the answers for this exercise, we let x represent the population proportion of the
invading type.
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
(a) In a population primarily consisting of A types with only a small proportion (x) of
invading T types, the A-type fitness is F(A) = 864(1 – x) + 936x = 864 + 72x and the T-type fitness is
F(T) = 792(1 – x) + 972x = 792 + 180x. F(A) > F(T) as long as 864 + 72x > 792 + 180x, or 72 > 108x, or
the population and Ns cannot prevent Ts from invading. A population of Ns invaded by Ts thus exhibits
neutral stability, where both the primary and secondary criteria for an ESS give ties. Since neither type is
more fit than the other, their proportions in the population will persist, only slightly adjusting as mutations
occur.
Against a group of mutant As, the N types have fitness F(N) = 972(1 – x) + 648x = 972 – 324x
(c) In a primarily T population, mutant As have fitness F(A) = 936(1 – x) + 864x = 936 –
72x, and the T-type fitness is F(T) = 972(1 – x) + 792x = 972 – 180x. F(T) > F(A) when 972 – 180x > 936
S3. (a) The payoff table follows:
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
Column
A T
(b) Let x be the population proportion of T players. Then the As’ expected years in jail are
20(1 – x) + 11x = 20 – 9x, and the Ts’ expected years in jail are 35(1 – x) + 6x = 35 – 29x. Then the T type
(c) See the payoff table below. The strategy N does not do well in this game. In a mixed
population that includes all three types, let x and y be the population proportions of T and N, respectively.
(b):
Column
A T N
S4. (a) The payoff table is shown below:
Male
Theater
(prop. y)
Movie
(prop. 1 – y)
(prop. 1 – x)
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
The diagram below shows the dynamics of the game:
(b) There are two ESS: (0, 0) and (1, 1).
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
S5. (a) The most obvious mixture to play is the mixed-strategy equilibrium of the two-player
(b) To calculate expected payoffs for pairs that include a Mixer type, remember that the
Mixer reports $100 with probability 0.4 and $50 with probability 0.6. So when a Mixer plays against a
The expected payoff when two Mixer types meet is a little more complicated, since there are four
cases to consider. With probability 0.4*0.4, both Mixers report $100. With probability 0.4*0.6, the first
The three-by-three table of expected payoffs with the Mixer type is then:
High Mixer Low
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
(c) Consider the case when a single High type attempts to invade a population entirely
composed of Mixer types. In this situation we need only the upper-left corner of the payoff table in part
(b):
High Mixer
In terms of m—the proportion of Mixer types in the population—the fitness of the High type is
100(1 – m) + 58m, whereas the fitness of the Mixer type is 82(1 – m) + 58m. When m = 1, it is true that
Now consider the case when a single Low type attempts to invade a population entirely composed
of Mixer types. Now we need only the lower-right corner of the payoff table in part (b):
Mixer Low
In terms of m—the proportion of Mixer types in the population—the fitness of the Low type is
58m + 50(1 – m), whereas the fitness of the Mixer type is 58m + 42(1 – m). When m = 1, the fitnesses of
Since either a High type or a Low type could successfully invade a population of Mixer types, the
Mixer phenotype is not an ESS of this game.
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
S6. (a) The fitness of the solar type, FS, is 2s + 3(1 – s) = 3 – s, and the fitness of the fossil fuel
There are three possible equilibria: an unstable monomorphic equilibrium where everyone uses
fossil fuels (s = 0), an unstable monomorphic equilibrium where everyone uses solar (s = 1), and a stable
(b) With the change in the (Solar, Solar) payoff, FS = ys + 3(1 – s) = 3 + (y – 3)s. There is no
change in FFF. At a polymorphic equilibrium, the fitness of the solar type is equal to the fitness of the
S7. (a) When t = 0.5, the fitness of tortoises is c * 0.5 + (–1) * 0.5 = 0.5c – 0.5, and the fitness of
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
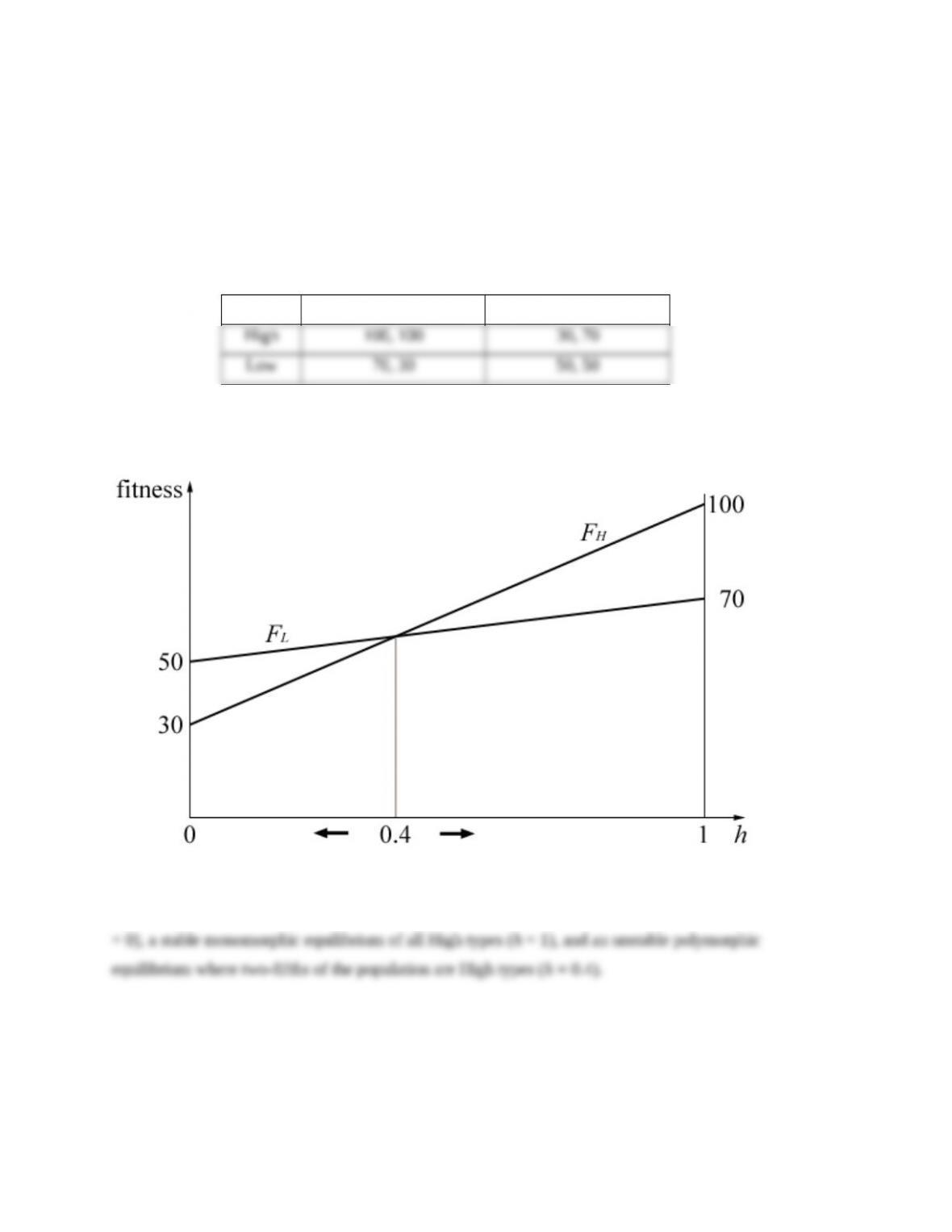
(b) When t = 0.1, the fitness of tortoises is c * 0.1 + (–1) * 0.9 = 0.1c – 0.9, and the fitness of
(c) When there is a population of pure tortoises (that is, when t = 1), the fitness of tortoises is
c * 1 + (–1) * 0 = c, and the fitness of hares is 1 * 1 + 0 * 0 = 1. If c = 1, tortoises and hares are equally fit
when t = 1, so an invading hare will at least hold its own against the tortoises. But really, after a hare has
(d) In terms of t and c, the fitness of tortoises is ct + (–1)(1 – t) = t + ct – 1. In terms of t, the
Note that as t approaches zero, c would need to be infinitely great for a tortoise to be more fit.
Regrettably, a single tortoise in a population of pure hares would never have a chance to have a pleasant
conversation with another tortoise. Thus—no matter the value of c—a single tortoise could never
successfully invade a population of pure hares.
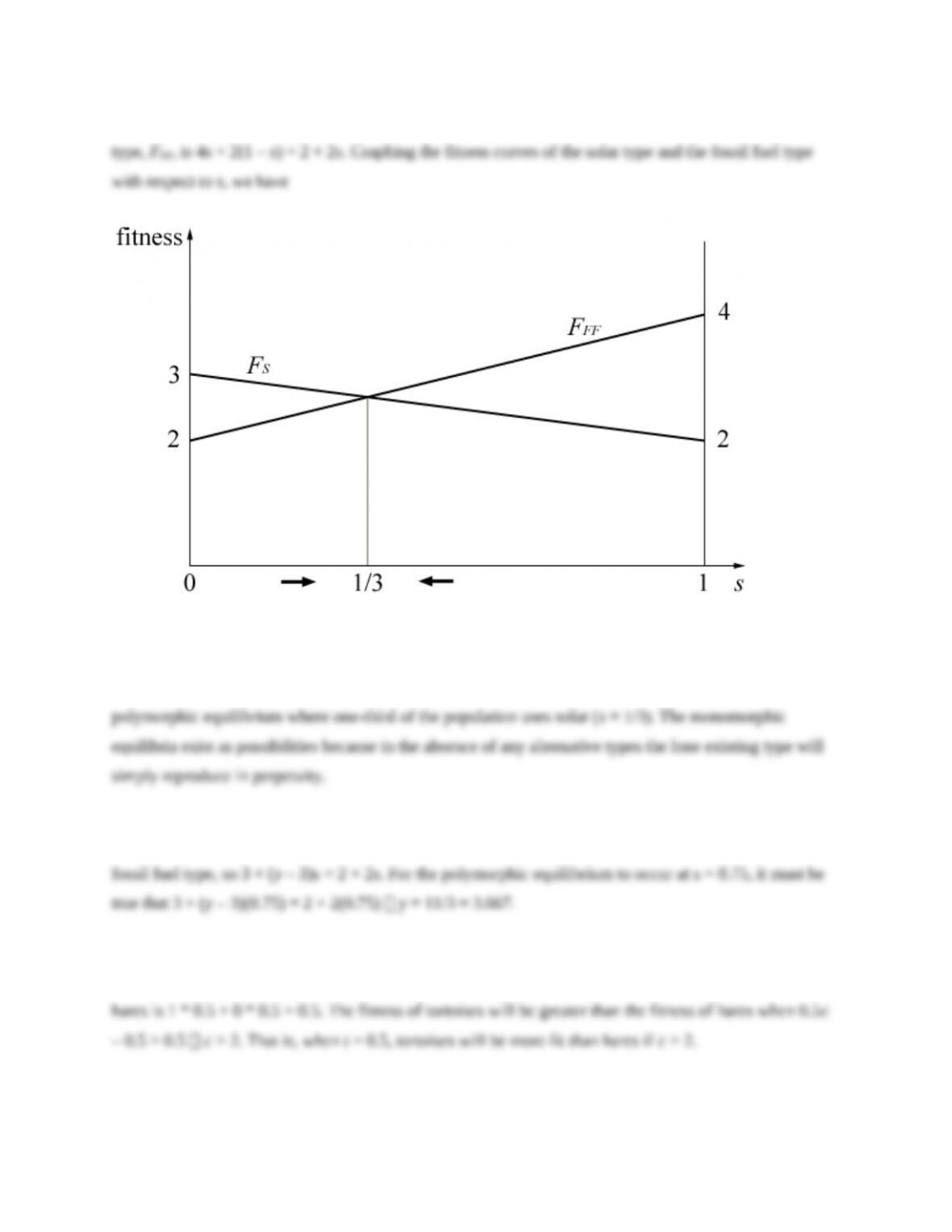
(e) In a polymorphic equilibrium, the fitness of tortoises must equal the fitness of hares. That
S8. (a) The fitness of X, FX, is 2x + 5(1 – x) = 5 – 3x.
The fitness of Y, FY, is 3x + 1(1 – x) = 1 + 2x.
(b) Following the expressions given for FX and FY in part (a) and given that x0 = 0.2, FX0 = 5 –
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
S9. (a) The fitness of the purple type, Fp, is 3g + 2(1 – g) = 2 + g.
(c) For there to be a polymorphic equilibrium, it must be the case that the fitness of purple
types is equal to the fitness of green types for some proportion of greens, g*, less than 1. For this
Graphing the fitness curve of the purple type and multiple fitness curves for green types of
varying levels of a helps us to visualize the mechanics of the game, as seen in the figure below:
The fitness of the purple type, Fp, is equal to the fitness of a given green type, Fg, whenever the
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
(d) The equilibrium proportion of green types, g*, in the stable polymorphic equilibrium is
the one where the fitness of the purple type is equal to the fitness of the green type:
2
2 4 ( 4) * 5
g a g g a
+ = + - Þ = -
Note that the expression for g* makes sense only as a proportion (which by definition must be
bounded between 0 and 1) when a ≤ 3. Reassuringly, this agrees nicely with the answer in part (c).
S10. Suppose the strategies are S1, S2, . . . , Sn, and the payoff of a player genetically programmed to
play i when matched against one genetically programmed to play j is Aij. Suppose the proportions of the
types are p1, p2, . . . , pn. Then the fitness of type i is
If strategy 1 is strictly dominated by strategy 2, then A1j < A2j for all j. The proportions sum to 1,
Next, suppose strategy 1 is weakly dominated by strategy 2. The two can have equal fitnesses if the
population consists of only those types against which the two have equal payoffs, but not if the population
Games of Strategy, Fourth Edition Copyright © 2015 W. W. Norton & Company
