978-0133915426 Chapter 17 Part 1

791

17–1.

SOLUTION

Thus,

Ans.Iy=1

3ml

2

m=rAl

=1

3rAl

3

=Ll

0

x2(rAdx)

Iy=L

M

x2dm

Determine the moment of inertia for the slender rod. The

rod’s density and cross-sectional area Aare constant.

Express the result in terms of the rod’s total mass m.

r

Iy

y

z

A

l

3

17–2.

The solid cylinder has an outer radius R, height h, and is

made from a material having a density that varies from its

center as where kand aare constants.

Determine the mass of the cylinder and its moment of

inertia about the zaxis.

r=k+ar2,

SOLUTION

Ans.

Ans.Iz=phR

4

2[k+2aR2

3]

Iz=2ph[kR

4

4+aR6

6]

Iz=2phLR

0

(kr

3+ar

5)dr

Iz=LR

0

r2(k+ar2)(2prdr)h

dI =r2dm =r2(r)(2prdr)h

m=phR

2(k+aR2

2)

m=2ph(kR2

2+aR4

4)

m=LR

0

(k+ar2)(2prdr)h

R

h

z

17–3.

Determ

i

ne t

h

e moment of

i

nert

i

a of t

h

e t

hi

n r

i

ng a

b

out the

zaxis.The ring has a mass m.

SOLUTION

Thus,

Ans.I

z

=mR

2

m=L2p

0

rARdu=2prAR

Iz=L2p

0

rA(Rdu)R2=2prAR

3

x

y

R

*17–4.

SOLUTION

Ans.kx=AIx

m=A50

3(200) =57.7 mm

=rpa50

2b(200)2

=rp(50)c1

2x2d200

0

m=Ldm =L200

0

pr(50x)dx

=rpa502

6b(200)3

=rpa502

2bc1

3x3d200

0

Ix=L1

2y2dm =1

2L200

0

50 x{pr(50x)} dx

dm =rpy2dx =rp(50x)dx

The paraboloid is formed by revolving the shaded area

around the xaxis. Determine the radius of gyration .The

density of the material is .r=5Mg>m3

kx

y

x

y250x

100 mm

17–5.

SOLUTION

Ans.kx=AIx

m=A86.17r

60.32r

=1.20 in.

m=L8

0

prx2/3 dx =60.32r

Ix=L8

0

1

2prx4/3 dx =86.17r

dI

x=1

2(dm)y2=1

2pry4dx

dm =rdV =rp y2dx

Determine the radius of gyration of the body. The

specific weight of the material is g=380 lb>ft3.

kx

y

x

2in.

y

3

=x

8in.

796

17–6.

The sphere is formed by revolving the shaded area around

the xaxis. Determine the moment of inertia and express

the result in terms of the total mass mof the sphere.The

material has a constant density r.

Ix

Thus,

Ans.Ix=2

5mr

2

=4

3rpr3

m=Lr

–r

rp(r2–x2)dx

=8

15 pr r5

Ix=Lr

–r

1

2rp(r2–x2)2dx

dIx=1

2rp(r2–x2)2dx

dm =rdV =r(py2dx)=rp(r2–x2)dx

x

y

x2+y2=r2

5

797

17–7.

The frustum is formed by rotating the shaded area around

the xaxis. Determine the moment of inertia and express

the result in terms of the total mass mof the frustum. The

frustum has a constant density .r

Ix

SOLUTION

Ans.Ix=93

70

mb2

m=L

m

dm =rp La

0

A

b2

a2x2+2b2

ax+b2

B

dx =7

3rpab2

=31

10rpab4

Ix=LdIx=1

2rp La

0

A

b4

a4x4+4b4

a3x3+6b4

a2x2+4b4

ax+b4

B

dx

dIx=1

2rp

A

b4

a4x4+4b4

a3x3+6b4

a2x2+4b4

ax+b4

B

dx

dIx=1

2dmy2=1

2rpy4dx

dm =rdV =rpy2dx =rp

A

b2

a2x2+2b2

ax+b2

B

dx

y

x

2b

b

–

axb

y

a

z

b

70

798

*17–8.

The hemisphere is formed by rotating the shaded area

around the yaxis. Determine the moment of inertia and

express the result in terms of the total mass mof the

hemisphere.The material has a constant density .r

Iy

Thus,

Ans.Iy=2

5mr

2

=rp

2cr4y–2

3r2y3+y5

5dr

0

=4rp

15 r5

Iy=L

m

1

2(dm)x2=r

2Lr

0

px4dy =rp

2Lr

0

(r2–y2)2dy

=rpcr2y–1

3y3dr

0

=2

3rp r3

V

0

x2y2r2

y

x

5

799

17–9.

SOLUTION

Thus,

Ans.Iy=m

6(a2+h2)

m=rV=1

2abhr

=1

12 abhr(a2+h2)

=abr[a2

3h3(h4–3

2h4+h4–1

4h4)+1

h(1

3h4–1

4h4)]

Iy=abrLk

0

[a3

3(h–z

h)3+z2(1 –z

h)]dz

=[b(a)(1 –z

h)dz](r)[a2

3(1 –z

h)2+z2]

=dm(x2

3+z2)

=1

12 dm(x2)+dm(x2

4)+dmz2

dIy=dIy+(dm)[(x

2)2+z2]

Determine the moment of inertia of the homogeneous

triangular prism with respect to the yaxis.Express the result

in terms of the mass mof the prism. Hint:For integration, use

thin plate elements parallel to the x–yplane and having a

thickness dz.

z

–h

––

a(x–a)z=

h

Ans:

Iy=

m

6

(

a2+h2

)

800

17–10.

The pendulum consists of a 4-kg circular plate and a

2-kg slender rod. Determine the radius of gyration of the

pendulum about an axis perpendicular to the page and

passing through point O.

Ans:

kO=2.17 m

O=

G+

=

c1

12

(2)

(

22

)

+2

(

1

2

)

d

+

c1

2

(4)

(

0.52

)

+4

(

2.52

)

d

=

28.17 kg

#

m

2

Thus, the radius of gyration is

kO=

AI

O

m

=

A28.17

4+2

=2.167 m =2.17 m Ans.

O

2 m

17–11.

The assembly is made of the slender rods that have a mass

per unit length of 3 kg

>

m. Determine the mass moment of

inertia of the assembly about an axis perpendicular to the

page and passing through point O.

O

0.8 m

0.4 m

SOLUTION

*17–12.

SOLUTION

Ans.=5.64 slug #ft2

=c1

2p(0.5)2(3)(0.5)2+3

10 a1

3bp(0.5)2(4)(0.5)2–3

10 a1

2bp(0.25)2(2)(0.25)2da490

32.2 b

Ix=1

2m1(0.5)2+3

10 m2(0.5)2–3

10 m3(0.25)2

D

etermine the moment of inertia of the solid steel assembly

about the xaxis. Steel has a specific weight of

.gst =490 lb>ft3

2ft3 ft

0.5 ft

0.25 ft

x

803

17–13.

SOLUTION

Ans.=7.67 kg #m2

=c2c1

12 (4)(1)2d+10(0.5)2d+18(0.5)2

IA=Io+md3

The wheel consists of a thin ring having a mass of 10 kg and

four spokes made from slender rods, each having a mass of

2kg. Determine the wheel’s moment of inertia about an

axis perpendicular to the page and passing through point A.

500 mm

Ans:

I

A=7.67

kg #m2

17–14.

SOLUTION

distance of from point Ocan be grouped as segment (2).

Mass Moment of Inertia:First, we will compute the mass moment of inertia of the

wheel about an axis perpendicular to the page and passing through point O.

The mass moment of inertia of the wheel about an axis perpendicular to the page

and passing through point Acan be found using the parallel-axis theorem

, where and .

Thus,

Ans.I

A=

84.94

+

8.5404(42)

=

221.58 slug

#

ft2

=

222 slug

#

ft2

d=4ftm=100

32.2 +8a20

32.2 b+15

32.2 =8.5404 slugIA=IO+md2

=84.94 slug #ft2

IO=a100

32.2 b(42)+8c1

12 a20

32.2 b(32)+a20

32.2 b(2.52)d+a15

32.2 b(12)

a1+3

2bft =2.5 ft

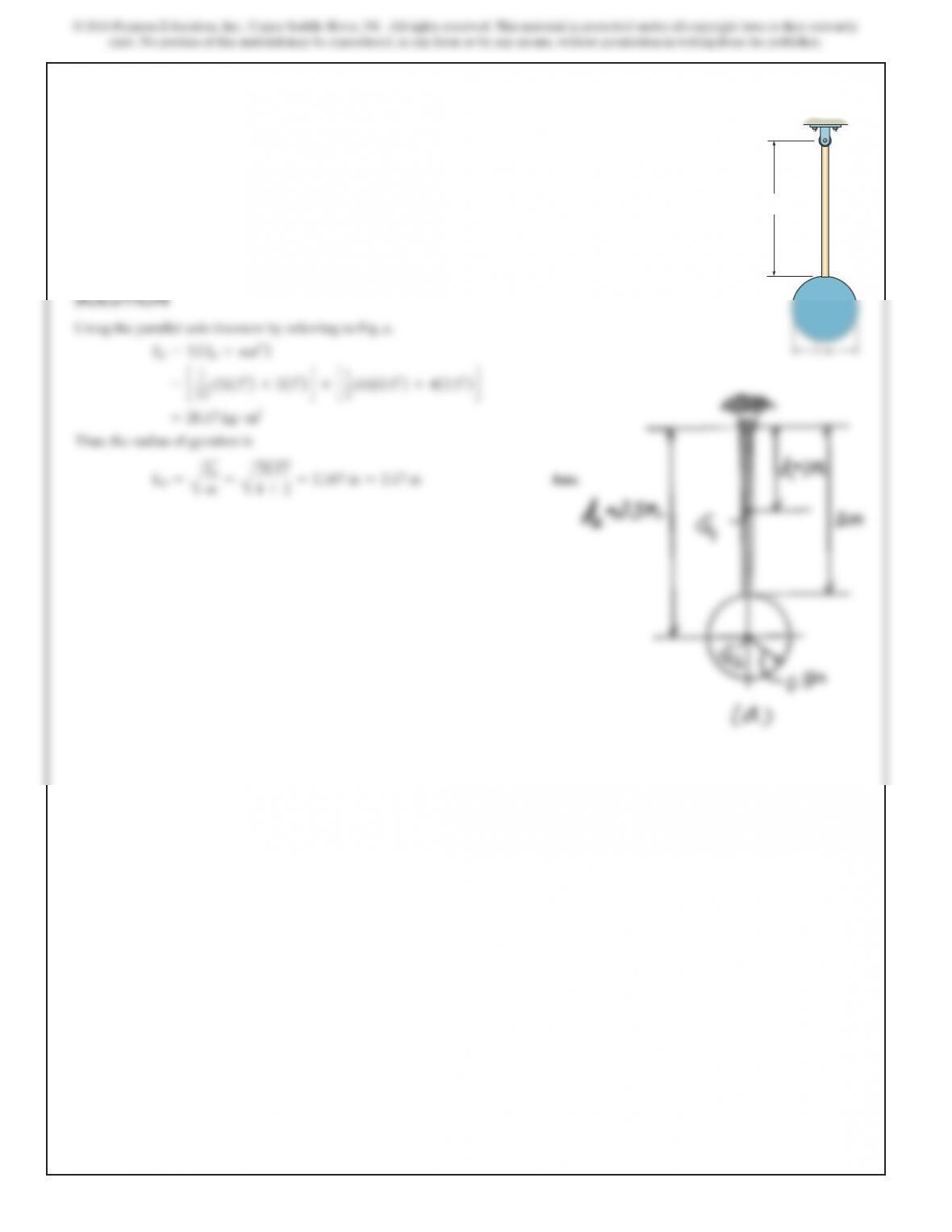
If the large ring,small ring and each of the spokes weigh

100 lb,15 lb,and 20 lb,respectively,determine the mass

moment of inertia of the wheel about an axis perpendicular

to the page and passing through point A.

O

1ft

4ft

17–15.

SOLUTION

Ans.IO=1.5987 +4.7233(1.4 sin 45°)2=6.23 kg #m2

m=50(1.4)(1.4)(0.05) –50(p)(0.15)2(0.05) =4.7233 kg

IO=IG+md2

=1.5987 kg #m2

IG=1

12

C

50(1.4)(1.4)(0.05)

DC

(1.4)2+(1.4)2

D

–1

2

C

50(p)(0.15)2(0.05)

D

(0.15)2

Determine the moment of inertia about an axis perpendicular

to the page and passing through the pin at O. The thin plate

has a hole in its center. Its thickness is 50 mm, and the

material has a density r =50 kg>m3.

150 mm

O

Ans:

*17–16.

SOLUTION

inertia of the plate about an axis perpendicular to the page and passing through point

Ofor each segment can be determined using the parallel-axis theorem.

Ans.=0.113 kg #m2

=c1

2(0.8p)(0.22)+0.8p(0.22)d–c1

12 (0.8)(0.22+0.22)+0.8(0.22)d

IO=©IG+md2

Determine the mass moment of inertia of the thin plate

about an axis perpendicular to the page and passing

through point O.The material has a mass per unit area of

.20 kg>m2

200 mm

O

807

17–17.

Determine the location

y

of the center of mass G of the

assembly and then calculate the moment of inertia about

an axis perpendicular to the page and passing through G.

The block has a mass of 3 kg and the semicylinder has a

mass of 5 kg.

Ans:

I

G=0.230 kg #m2

SOLUTION

G

400 mm

300 mm

200 mm

O

y

–

17–18.

Determine the moment of inertia of the assembly about an

axis perpendicular to the page and passing through point O.

The block has a mass of 3 kg, and the semicylinder has a

mass of 5 kg.

G

400 mm

300 mm

200 mm

O

y

–

SOLUTION

1

809

17–19.

Determine the moment of inertia of the wheel about an

axis which is perpendicular to the page and passes through

the center of mass G. The material has a specific weight

g

=

90 lb

>

ft

3

.

Ans:

I

G=118 slug #ft2

SOLUTION

1

G

O

0.5 ft

0.25 ft

1 ft

2 ft

*17–20.

Determine the moment of inertia of the wheel about an axis

which is perpendicular to the page and passes through point O.

The material has a specific weight g

=

90 lb

>

ft

3

.

G

O

0.5 ft

1 ft

0.25 ft

1 ft

2 ft

SOLUTION

90