Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.1. Starting from (8.5) and working in (x,y,z) Cartesian coordinates, determine an
equation that specifies the locus of points that defines a wave crest. Verify that the travel speed
of the crests in the direction of K = (k, l, m) is c =
ω
/|K|. Can anything be determined about the
wave crest travel speed in other directions?
Solution 8.1. The phase of the waveform in (8.5) is
K⋅x−
ω
t
. Thus wave crests are specified
by:
K⋅xcrest −
ω
t=2n
π
,
since cos(2n
π
) = 1. In (x,y,z) Cartesian coordinates with K = (k, l, m), this is the equation for a
series of planes:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.2. For ka << 1, use the potential for linear deep water waves,
φ
(z,x,t)=a
ω
k
( )
ekz sin(kx −
ω
t)
and the waveform
η
(x,t)=acos kx −
ω
t
( )
+
α
ka2cos 2 kx −
ω
t
( )
[ ]
to show that:
a) with an appropriate choice of the constant
α
, the kinematic boundary condition (8.16) can be
satisfied for terms proportional to (ka)0 and (ka)1 once the common factor of a
ω
has been divided
out, and
b) with an appropriate choice of the constant
γ
, the dynamic boundary condition (8.19) can be
satisfied for terms proportional to (ka)0, (ka)1, and (ka)2 when
ω
2 = gk(1 +
γ
k2a2) once the
common factor of ag has been divided out.
Solution 8.2. a) First determine the horizontal (u) and vertical (w) velocities from the given
velocity potential:
u=
∂φ
∂
x=a
ω
k
ekz kcos(kx −
ω
t)
[ ]
=a
ω
ekz cos(kx −
ω
t)
,
w=
∂φ
∂
z=a
ω
k
kekz
[ ]
sin(kx −
ω
t)=a
ω
ekz sin(kx −
ω
t)
,
and the derivatives of the surface waveform:
∂η
∂
t=
ω
asin kx −
ω
t
( )
+2
ωα
ka2sin 2kx −
ω
t
( )
[ ]
,
∂η
∂
x=−ka sin kx −
ω
t
( )
−2
α
k2a2sin 2kx −
ω
t
( )
[ ]
.
Use these results and the surface waveform in (8.16),
∂φ
∂
z
$
%
& ‘
(
)
z=
η
=
∂η
∂
t+
∂η
∂
x
∂φ
∂
x
$
%
& ‘
(
)
z=
η
:
a
ω
ek
η
sin(kx −
ω
t)=
ω
asin kx −
ω
t
( )
+2
ωα
ka2sin 2kx −
ω
t
( )
[ ]
+ −ka sin kx −
ω
t
( )
−2
α
k2a2sin 2kx −
ω
t
( )
[ ]
( )
a
ω
ek
η
cos(kx −
ω
t).
To simplify, let
β
= kx –
ω
t, and divide out common factors to find:
ek
η
sin
β
=sin
β
+2
α
kasin(2
β
)−ka sin
β
+2
α
k2a2sin(2
β
)
( )
ek
η
cos
β
.
Since matching up through terms proportional to ka is necessary, the exponential function should
be expanded through its first-order term,
ek
η
≅1+ka cos
β
for ka << 1, so
1+ka cos
β
( )
sin
β
=sin
β
+2
α
ka sin(2
β
)−ka sin
β
+2
α
k2a2sin(2
β
)
( )
1+ka cos
β
( )
cos
β
.
Perform the various multiplications, and group terms that are proportional to (ka)0 and (ka)1.
sin
β
+ka cos
β
sin
β
( )
=sin
β
+ka 2
α
sin(2
β
)−sin
β
cos
β
( )
+k2a2…
( )
.
The (ka)0 terms match. The (ka)1 terms will match if:
cos
β
sin
β
=2
α
sin(2
β
)−sin
β
cos
β
→2cos
β
sin
β
=2
α
sin(2
β
)
,
and this equation is satisfied when
α
= 1/2.
b) First determine the time derivative of the velocity potential and use the notation of part a):
∂φ
∂
t=a
ω
k
ekz −
ω
cos(kx −
ω
t)
[ ]
=−a
ω
2
k
ekz cos
β
.
After using the Bernoulli equation, the dynamic boundary condition is:
∂φ
∂
t+1
2
u2+gz
$
%
& ‘
(
)
z=
η
=0→ − a
ω
2
kek
η
cos
β
+
ρ
2a2
ω
2e2k
η
cos2
β
+a2
ω
2e2k
η
sin2
β
( )
+g
η
=0
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.3. The field equation for surface waves on a deep fluid layer in two dimensions (x,z)
is:
∂
2
φ ∂
x2+
∂
2
φ ∂
z2=0
, where
φ
is the velocity potential,
∇
φ
=(u,w)
. The linearized free-
surface boundary conditions and the bottom boundary condition are:
∂φ ∂
z
( )
z=0≅
∂η ∂
t
,
∂φ ∂
t
( )
z=0+g
η
≅0
, and
∂φ ∂
z
( )
z→−∞ =0
,
where z =
η
(x,t) defines the free surface, gravity g points downward along the z-axis, the
undisturbed free surface lies at z = 0. The goal of this problem is to develop the general solution
for these equations without assuming a sinusoidal form for the free surface as was done in
Section 8.1and 8.2.
a) Assume
φ
(x,z,t)=Λ(x,t)Z(z)
, and use the field equation and bottom boundary condition to
show that
φ
(x,z,t)=Λ(x,t)exp(+kz)
, where k is a positive real constant.
b) Use the results of part a) and the remaining boundary conditions to show:
∂
2Λ
∂
t2+gkΛ=0
and
∂
2Λ
∂
x2+k2Λ=0
.
c) For a fixed value of k, find Λ(x,t) in terms of four unknown amplitudes A, B, C, and D.
d) For the initial conditions:
η
= h(x) and ∂
η
/∂t =
˙
h (x)
at t = 0, determine the general form of
φ
(x, z, t).
Solution 8.3. a) Insert
φ
(x.z,t)=Λ(x,t)Z(z)
into the field equation
∂
2
φ ∂
x2+
∂
2
φ ∂
z2=0
and
divide by
φ
to find:
1
Λ
∂
2Λ
∂
x2+1
Z
d2Z
dz2=0
. The first term depends only on x and t while the second
depends only on z; thus each must be constant to ensure the equation is satisfied for all possible
(x, z, t). Therefore set the first term equal to –k2 and the second term equal to +k2. Then, the
equation involving Z(z) is
d2Z dz2−k2Z=0
which has the solution: Z = A+e+kz + A–e–kz, where
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Λ(x,t)=#
A sin(kx)sin t gk
( )
+#
B sin(kx)cos t gk
( )
+#
C cos(kx)sin t gk
( )
+#
D cos(kx)cos t gk
( )
.
Unfortunately, this form hides the wave-propagation character of the solution, but with the use of
trigonometric angle-sum and angle-difference formulae for the sine and cosine functions, the
above form for Λ can be written:
Λ(x,t)=Asin kx −t gk
( )
+Bcos kx −t gk
( )
+Csin kx +t gk
( )
+Dcos kx +t gk
( )
,
where 2A = B´ – C´, 2B = A´ + D´, 2C = B´ + C´, and 2D = –A´ + D´.
d) The above form for Λ is only valid when k ≥ 0, so k may take on any non-negative value.
Thus, the final solution must be of the form:
φ
(x,z,t)=
A(k)sin kx −t gk
( )
+B(k)cos kx −t gk
( )
+
C(k)sin kx +t gk
( )
+D(k)cos kx +t gk
( )
$
%
&
‘
&
(
)
&
*
&
ekz dk
0
+∞
∫
.
Now combine the initial and boundary conditions. The first boundary condition evaluated at t = 0
implies:
∂φ ∂
z
( )
(z,t)=0=
∂η ∂
t
( )
t=0=˙
h (x)
, or
˙
h (x)=A(k)+C(k)
[ ]
sin kx
( )
+B(k)+D(k)
[ ]
cos kx
( )
{ }
kdk
0
+∞
∫
.
The second boundary condition evaluated at t = 0 implies:
∂φ ∂
t
( )
(z,t)=0=−g
η
( )
t=0=−gh(x)
, or
−gh(x)=gk −A(k)+C(k)
[ ]
cos kx
( )
+B(k)−D(k)
[ ]
sin kx
( )
{ }
dk
0
+∞
∫
The final formulae for A, B, C, and D are found from considerations of symmetry about x = 0:
˙
h (x)−˙
h (−x)=2k A(k)+C(k)
[ ]
sin kx
( )
dk
0
+∞
∫
,
˙
h (x)+˙
h (−x)=2k B(k)+D(k)
[ ]
cos kx
( )
dk
0
+∞
∫
,
−g h(x)+h(−x)
( )
=gk −A(k)+C(k)
[ ]
cos kx
( )
dk
0
+∞
∫
, and
−g h(x)−h(−x)
( )
=gk B(k)−D(k)
[ ]
sin kx
( )
dk
0
+∞
∫
and can be evaluated in formal terms via inverse sine and cosine transforms.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.4. Derive (8.37) from (8.27).
Solution 8.4. Use the velocity components specified in (8.27), and the definition of the stream
function in two-dimensions (x, z):
u=
∂ψ
∂
z=a
ω
cosh k(z+H)
( )
sinh kH
( )
cos(kx −
ω
t)
, and
w=−
∂ψ
∂
x=a
ω
sinh k(z+H)
( )
sinh kH
( )
sin(kx −
ω
t)
.
Integrate each equation to find:
ψ
=a
ω
k
sinh k(z+H)
( )
sinh kH
( )
cos(kx −
ω
t)+f(x)
, and
ψ
=a
ω
k
sinh k(z+H)
( )
sinh kH
( )
cos(kx −
ω
t)+g(z)
.
where f and g are single-variable functions of integration. These are consistent when f(x) = g(y) =
constant, and this constant can be set to zero without loss of generality. The final result is (8.37):
ψ
=a
ω
k
sinh k(z+H)
( )
sinh kH
( )
cos(kx −
ω
t)
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.5. Consider stationary surface gravity waves in a rectangular container of length L
and breadth b, containing water of undisturbed depth H. Show that the velocity potential
φ
=
Acos(m
π
x/L)cos(n
π
y/b)cosh[k(z + H)]e–i
ω
t, satisfies the Laplace equation and the wall boundary
conditions, if (m
π
/L)2 + (n
π
/b)2 = k2. Here m and n are integers. To satisfy the linearized free-
surface boundary condition, show that the allowable frequencies must be
ω
2 = gk tanh(kH).
[Hint: combine the two boundary conditions (8.18) and (8.21) into a single equation ∂2
φ
/∂t2 = −g
∂
φ
/∂z at z = 0.]
Solution 8.5. Start from
φ
=Acos m
π
x L
( )
cos n
π
y b
( )
cosh k(z+H)
[ ]
e−i
ω
t
and compute
velocities.
u=
∂φ
∂
x=−A m
π
L
( )
sin m
π
x L
( )
cos n
π
y b
( )
cosh k(z+H)
[ ]
e−i
ω
t
which implies u = 0 at x = 0 and x = L, so the x-direction BCs are satisfied. Similarly,
v=
∂φ
∂
y=−A n
π
b
( )
cos m
π
x L
( )
sin n
π
y b
( )
cosh k(z+H)
[ ]
e−i
ω
t
which implies v = 0 at y = 0 and y = b, so the y-direction BCs are satisfied. The Laplacian is:
∂
2
φ
∂
x2+
∂
2
φ
∂
y2+
∂
2
φ
∂
z2=−m2
π
2
L2−n2
π
2
b2+k2
&
‘
(
)
*
+
Acos m
π
x L
( )
cos n
π
y b
( )
cosh k(z+H)
[ ]
e−i
ω
t
,
and it equals zero when:
k2=m2
π
2
L2+n2
π
2
b2
.
The linearized free surface boundary conditions are:
∂η ∂
t=
∂φ ∂
z
and
∂φ ∂
t=−g
η
at z = 0,
which can be combined to get:
∂
2
φ ∂
t2=−g
∂η ∂
t=−g
∂φ ∂
z
at z = 0.
Using the given potential, this requires
A(−i
ω
)2cos m
π
x L
( )
cos n
π
y b
( )
cosh k(z+H)
[ ]
e−i
ω
t
[ ]
z=0
=−gAk cos m
π
x L
( )
cos n
π
y b
( )
sinh k(z+H)
[ ]
e−i
ω
t
[ ]
z=0
,
or
−
ω
2cosh kH
[ ]
=−gk sinh kH
[ ]
which can be written:
ω
2=gk tanh kH
[ ]
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.6. A lake has the following dimensions L = 30 km, b = 2 km, and H = 100 m. If the
wind sets up the mode m = 1 and n = 0, show that the period of the oscillation is 32 min.
Solution 8.6. Use the results of Exercise 8.5:
k2=m2
π
2
L2+n2
π
2
b2
and
ω
2=gk tanh kH
[ ]
,
and eliminate k to find:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.7. Fill a square or rectangular cake pan half-way with water. Do the same for a round
frying pan of about the same size. Agitate the water by carrying the two pans (outside) while
walking briskly at a consistent pace on a horizontal surface.
a) Which shape lends itself better to spilling?
b) At what portion of the perimeter of the rectangular pan does spilling occur most readily?
c) Explain your observations in terms of standing wave modes.
Solution 8.7. a) For the pans tested by the third author, the water usually spilled out of the square
or rectangular pan first.
b) The water almost always left the square or rectangular pan from a corner.
c) All of the resonant modes of the rectangular pan have maximum vertical surface displacement
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.8. Use (8.27), (8.28), and (8.38), to prove (8.39).
Solution 8.8. Equation (8.38) specifies a double integration,
Ek=
ρ
2
λ
u2+w2
( )
−H
0
∫
0
λ
∫dzdx
, (8.38)
involving the two velocity components given by (8.27):
=e2kH
4
1
2k−e−2kH
2k
!
“
#$
%
&+H
2−e−2kH
4
1
2k−e+2kH
2k
!
“
#$
%
&
=1
8k
e2kH −1+4kH −e−2kH +1
( )
=1
8k
e2kH +4kH −e−2kH
( )
sinh2k(z+H)
( )
−H
0
∫dz =1
4
e2k(z+H)−2+e−2k(z+H)
( )
−H
0
∫dz
=e2kH
4
e2kz
−H
0
∫dz −1
2
dz
−H
0
∫+e−2kH
4
e−2kz
−H
0
∫dz
=e2kH
4
e2kz
2k
#
$
%&
‘
(
−H
0
−H
2+e−2kH
4
e−2kz
−2k
#
$
%&
‘
(
−H
0
=e2kH
4
1
2k−e−2kH
2k
#
$
%&
‘
(−H
2−e−2kH
4
1
2k−e+2kH
2k
#
$
%&
‘
(
=1
8k
e2kH −1−4kH −e−2kH +1
( )
=1
8k
e2kH −4kH −e−2kH
( )
Thus, wave kinetic energy becomes:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.9. Show that the group velocity of pure capillary waves in deep water, for which the
gravitational effects are negligible, is cg = (3/2)c.
Solution 8.9. For surface waves in the presence of gravity and surface tension, the dispersion
relationship is given by (8.56):
ω
=k g +
σ
k2
ρ
%
&
‘
(
)
*
tanh kH
( )
.
When gravity is negligible, this simplifies to:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.10. Assuming deep water, plot the group velocity of surface gravity waves, including
surface tension
σ
, as a function of
λ
for water at 20 °C (
ρ
= 1000 kg/m3 and
σ
= 0.074 N/m).
a) Show that the group velocity is
cg=1
2
g
k
1+3
σ
k2
ρ
g
1+
σ
k2
ρ
g
.
b) Show that this becomes minimum at a wave number given by
σ
k2
ρ
g=2
3−1.
c) Verify that cg min = 17.8 cm/s.
Solution 8.10. a) Start from (8.56):
ω
=k g +
σ
k2
ρ
%
&
‘
(
)
*
tanh kH
( )
. In deep water tanh(kH) ≈ 1, so
this simplifies to:
ω
≅gk +
σ
k3
ρ
. The group velocity in this case is:
cg=
∂ω
∂
k=
∂
∂
kgk +
σ
k3
ρ
=1
2gk +
σ
k3
ρ
g+3
σ
k2
ρ
&
‘
(
)
*
+ =1
2
g
k
1+3
σ
k2
ρ
g
1+
σ
k2
ρ
g
.
This relationship is plotted here; group speed is on the vertical axis in m/s and wavelength is on
the horizontal axis in cm.
b) The minimum group speed is found by differentiating cg with respect to k, setting this
derivative equal to zero, solving for kmin, and then evaluating cg at kmin.
!”
!#$”
!#%”
!#&”
!#'”
!#(“
!#)”
!#*”
!#+”
!#,”
!” %!” ‘!” )!” +!” $!!” $%!” $’!” $)!” $+!” %!!”
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.11. The energy propagation characteristics of sinusoidal deep-water capillary-gravity
waves follow those of pure gravity waves when corrections are made for the influence of surface
tension. Assume a waveform shape of
η
(x,t) = acos(kx –
ω
t) for the following items.
a) Show that the sum of the wave’s kinetic and potential energies (per unit surface area) can be
written:
E=Ek+Ep=1
2
ρ
a2
g
where
g=g+k2
σ ρ
.
b) Determine the wave energy flux EF (per unit length) from
<Begin Equation>
EF =
ω
2
π
!
p u
−∞
0
∫dz −
σ
t⋅u
[ ]
z=0
&
‘
()
*
+dt
0
2
π ω
∫
,
</End Equation>
where t is the surface tangent vector, and the extra term involving
σ
represents energy transfer
via surface tension.
c) Use the results of parts a) and b) to show that EF = Ecg, where cg is the group velocity
determined in Exercise 8.10 part a).
Solution 8.11. a) The kinetic and potential energies of sinusoidal deep-water capillary gravity
waves can be written:
Ek=
ρ
2
λ
u2+w2
( )
−H
0
∫
0
λ
∫dzdx
, and
Ep=
ρ
g
λ
z
0
η
∫dz dx
0
λ
∫+
σ
λ
1+∂
η
∂x
#
$
%&
‘
(
2
−1
#
$
%
%
&
‘
(
(dx
0
λ
∫
,
where the second term in the potential energy is the surface tension contribution. Using (8.47)
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
b) From the problem statement, the energy flux crossing any fixed x-location is:
EF =
ω
2
π
!
p u
−∞
0
∫dz −
σ
t⋅u
[ ]
z=0
&
‘
()
*
+dt
0
2
π ω
∫
.
The pressure fluctuation p´ is given by (8.30) so the linearized Bernoulli equation implies:
≅ −
σ
a
ω
cos(kx −
ω
t)−a2k
ω
sin2(kx −
ω
t)
( )
and the approximation is valid when ka << 1, which is the case here.
At any location, the time average of cos(kx –
ω
t) is zero, while the time average of
cos2(kx –
ω
t) and sin2(kx –
ω
t) are both 1/2. Thus,
EF =
ρ
a2
ω
3
4k2+
σ
a2k
ω
2
.
c) To show that EF = Ecg, where cg is the group velocity determined in Exercise 8.10 part a),
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 8.12. The effect of viscosity on the energy of linear deep-water surface waves can be
determined from the wave motion’s velocity components and the viscous dissipation (4.58).
a) For incompressible flow, the viscous dissipation of energy per unit mass of fluid is
ε
=2
µρ
( )
Sij
2
where Sij is the strain rate tensor and µ is the fluid’s viscosity. Determine
ε
using
(8.47).
b) The total wave energy per unit surface area, E, for a linear sinusoidal water wave with
amplitude a is given by (8.42). Assume that a is function time, set dE/dt = –
ε
, and show that a(t)
= a0exp[–2(µ/
ρ
)k2t] where a0 is the wave amplitude at t = 0.
c) Using a nominal value of µ/
ρ
= 10–6 m2/s for water, determine the time necessary for an
amplitude reduction of 50% for water-surface waves having
λ
= 1 mm, 1 cm, 10 cm, 1 m, 10 m,
and 100 m.
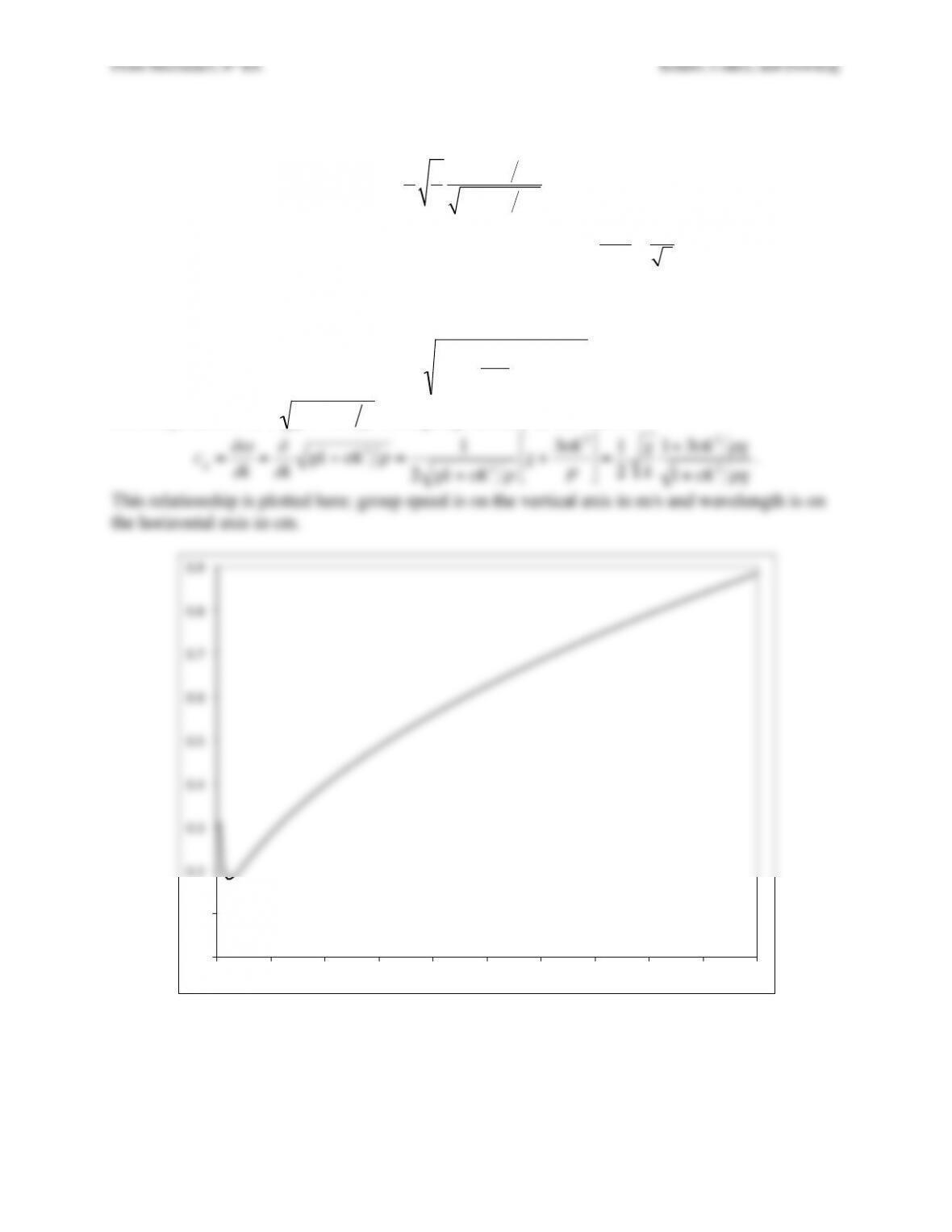
d) Convert the times calculated in c) to travel distances by multiplication with an appropriate
group speed. Remember to include surface tension. Can a typhoon located near New Zealand
produce increased surf on the coast of North America? [The circumference of the earth is
approximately 40,000 km].
Solution 8.12. a) First calculate the stress tensor using the velocity components specified by
(8.47):
u=a
ω
ekz cos(kx −
ω
t)
and
w=a
ω
ekz sin(kx −
ω
t)
.
Sij =1
2
∂
ui
∂
xj
+
∂
uj
∂
xi
#
$
%
%
&
‘
(
( =
∂
u
∂
x1
2
∂
u
∂
z+
∂
w
∂
x
( )
1
2
∂
w
∂
x+
∂
u
∂
z
( )
∂
w
∂
z
)
*
+
,
–
.
=a
ω
kekz −sin(kx −
ω
t) cos(kx −
ω
t)
cos(kx −
ω
t) sin(kx −
ω
t)
)
*
+
,
–
.
.
Now compute the viscous kinetic-energy dissipation per unit mass:
where the deep-water dispersion relationship
ω
2 = gk has been used to reach the final form.
Integrating the differential equation represented by the extreme ends of this extended equality
produces:
E=E0exp −4
µρ
( )
k2t
{ }
, or in terms of wave amplitude:
a=a0exp −2
µρ
( )
k2t
{ }
,
where E0 and a0 are the wave energy and amplitude, respectively, at t = 0.