Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
=p∞+1
2
ρ
U2
( )
π
a2−2a2p∞+1
2
ρ
U21−9
4sin2
θ
( )
[ ]
sin2
θ
d
θ
θ
=0
π
∫
=p∞+1
2
ρ
U2
( )
π
a2−2a2p∞+1
2
ρ
U2
[ ]
sin2
θ
d
θ
π
∫−2a21
2
ρ
U2
( )
−9
4
( )
sin4
θ
d
θ
π
∫
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.44. The flow-field produced by suction flow into
a round vacuum cleaner nozzle held above a large flat
surface can be easily investigated with a simple experiment,
and analyzed via potential flow in (R,
ϕ
, z)-cylindrical
coordinates with the method of images.
a) Do the experiment first. Obtain a vacuum cleaner that has
a hose for attachments. Remove any cleaning attachments
(brush, wand, etc) or unplug the hose from the cleaning
head, and attach an extension hose or something with a
round opening (~4 cm diameter is recommended). Find a
smooth dry flat horizontal surface that is a ~0.5 meter or
more in diameter. Sprinkle the central 1/3 of the surface
with a light granular material that is easy to see (granulated sugar, dry coffee grounds, salt, flour,
talcum powder, etc. should work well). The grains should be 1/2 to 1 mm apart on average. Turn
on the vacuum cleaner and lower the vacuum hose opening from ~0.25 meter above the surface
toward the surface with the vacuum opening facing toward the surface. When the hose gets to
within about one opening diameter of the surface or so, the granular material should start to
move. Once the granular material starts moving, hold the hose opening at the same height or lift
the hose slightly so that grains are not sucked into it. If many grains are vacuumed up, distribute
new ones in the bare spot(s) and start over. Once the correct hose-opening-to-surface distance is
achieved, hold the hose steady and let the suction airflow of the vacuum cleaner scour a pattern
into the distributed granular material. Describe the shape of the final pattern, and measure any
relevant dimensions.
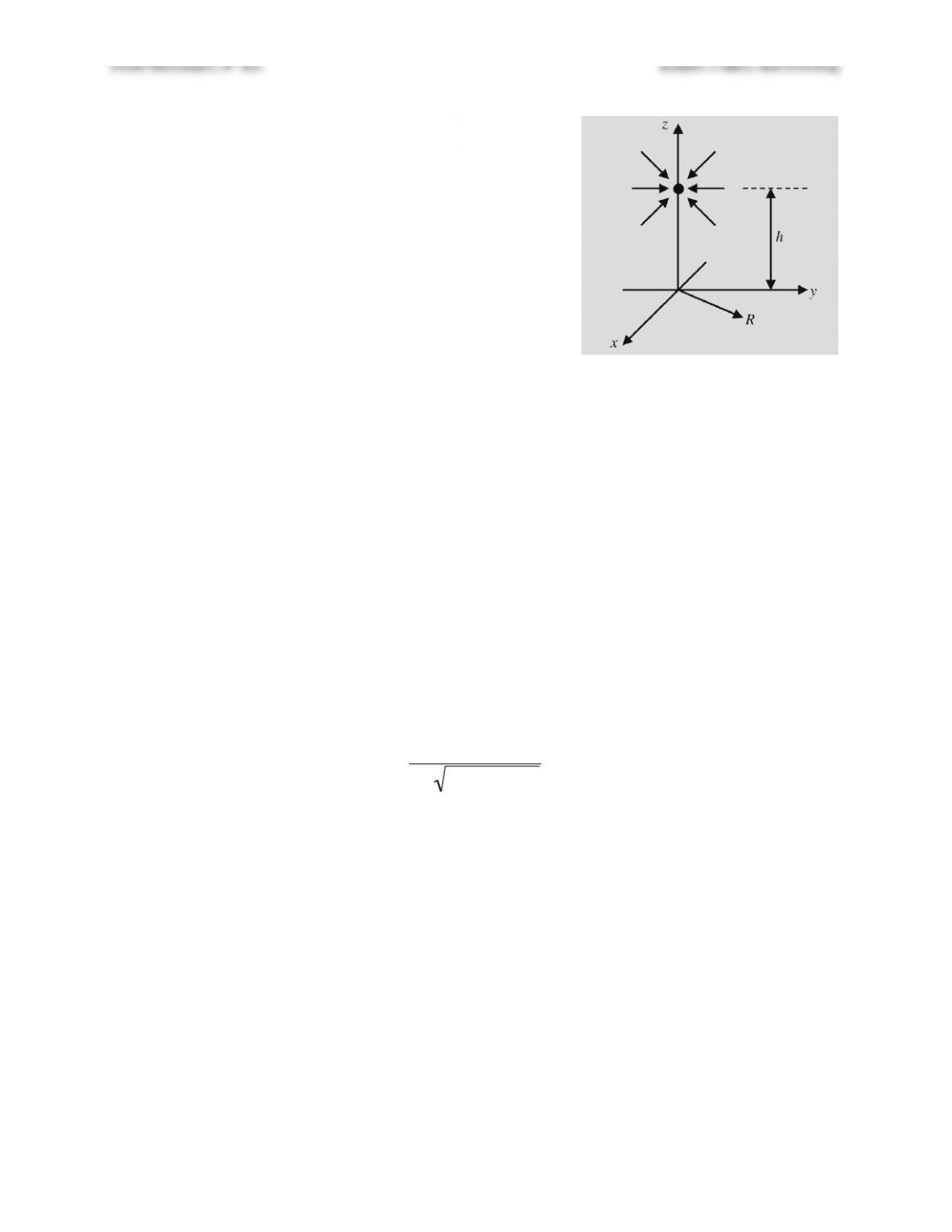
Now see if ideal flow theory can explain the pattern observed in part a). As a first
approximation, the flow field near the hose inlet can be modeled as a sink (a source with strength
–Q) above an infinite flat boundary since the vacuum cleaner outlet (a source with strength +Q)
is likely to be far enough away to be ignored. Denote the fluid density by
ρ
, the pressure far
away by p∞, and the pressure on the flat surface by p(R). The potential for this flow field will be
the sum of two terms:
φ
(R,z)=+Q
4
π
R2+(z−h)2+K(R,z)
b) Sketch the streamlines in the y–z plane for z > 0.
c) Determine K(R,z).
d) Use dimensional analysis to determine how p(R) – p∞ must depend on
ρ
, Q, R, and h.
e) Compute p(R) – p∞ from the steady Bernoulli equation. Is this pressure distribution consistent
with the results of part a)? Where is the lowest pressure? (This is also the location of the highest
speed surface flow). Is a grain at the origin of coordinates the one most likely to be picked up by
the vacuum cleaner?
Solution 7.44. a) The pattern scoured in the granular material is axisymmetric. The scoured
region is a ring that is a little larger than the vacuum cleaner opening. A pile of the granular
material is left directly below the center of the vacuum cleaner opening.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
c) Based on the method of images, K must represent a sink at z = –h, so:
K(R,z)=+Q
4
π
R2+(z+h)2
d) 5 parameters – 3 dimensions = 2 groups. Clearly
Π1=R h
. A little more effort yields:
( )
[ ]
( )
[ ]
)
,
Dividing out all the non-zero factors and parameters yields:
R1−2R h
( )
2
( )
=0
, which implies: R
= 0, or
R=h2
. The second answer matches (within experimental accuracy) the radius of the
ring on the surface where the scouring was most complete in the experiment. The first answer, R
= 0, is a stagnation point (a pressure maximum) so a grain located there is not likely to be picked
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.45. There is a point source of strength Q (m3/s) at the origin, and a uniform line sink
of strength k = Q/a extending from z = 0 to z = a. The two are combined with a uniform stream U
parallel to the z-axis. Show that the combination represents the flow past a closed surface of
revolution of airship shape, whose total length is the difference of the roots of:
z2
a2
z
a±1
“
#
$ %
&
‘ =Q
4
π
Ua2
Solution 7.45. From the symmetry of the flow, the
stagnation points that define the length of the body must
lie on the z-axis. Consider first the stagnation point, P, to
d!
!
U
P
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercsie 7.46. Using a computer, determine the surface contour of an axisymmetric half-body
formed by a line source of strength k (m2/s) distributed uniformly along the z-axis from z = 0 to z
= a and a uniform stream. The nose of this body is more pointed than that formed by the
combination of a point source and a uniform stream. From a mass balance, show that far
downstream the radius of the half-body is
r=ak
π
U
.
Solution 7.46. The Stokes stream function for this flow is given by:
ψ
=1
2
UR2−k
4
π
(z−
ζ
)d
ζ
(z−
ζ
)2+R2
0
a
∫=1
2
UR2+k
4
π
(z−a)2+R2−z2+R2
( )
,
where the final equality follows from evaluating the integral. The body contour will follow the
!”
!#$”
%”
&%” &!#$” !” !#$” %” %#$” ‘”
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.47. Consider the radial flow induced by the collapse of a spherical cavitation bubble
of radius R(t) in a large quiescent bath of incompressible inviscid fluid of density
ρ
. The pressure
far from the bubble is p∞. Ignore gravity.
a) Determine the velocity potential
φ
(r,t) for the radial flow outside the bubble.
b) Determine the pressure p(R(t), t) on the surface of the bubble.
c) Suppose that at t = 0 the pressure on the surface of the bubble is p∞, the bubble radius is Ro,
and its initial velocity is
−˙
R
o
(i.e. the bubble is shrinking), how long will it take for the bubble to
completely collapse if its surface pressure remains constant?
Solution 7.47. a) All of the flow will be in the radial direction. Thus:
∇2
φ
=1
r2
∂
∂
r
r2
∂φ
∂
r
%
&
‘ (
)
* =0
.
Away from r = 0, this equation can be integrated directly to find:
φ
=−A/r
, where A may be a
function of time. To evaluate A, match the radial fluid velocity at the surface of the sphere to the
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.48. Derive the apparent mass per unit
depth into the page of a cylinder of radius a that
travels at speed
Uc(t)=dxcdt
along the x-axis in
a large reservoir of an ideal quiescent fluid with
density
ρ
. Use an appropriate Bernoulli equation
and the following time-dependent two-dimensional
potential:
φ
(x,y,t)=−a2Uc(x−xc)
(x−xc)2+y2
, where xc(t) is location of the center of the cylinder, and the
Cartesian coordinates are x and y. [Hint: steady cylinder motion does not contribute to the
cylinder’s apparent mass; keep only the term (or terms) from the Bernoulli equation necessary to
determine apparent mass].
Solution 7.48. In an ideal incompressible fluid, the hydrodynamic loads on the moving cylinder
will occur through pressure forces and the pressure will be set by the unsteady Bernoulli
equation (UBE).
ρ∂φ
∂
t+1
2
ρ
∇
φ
2+
ρ
gy +p=p∞
or
p∞−p=
ρ∂φ
∂
t+1
2
ρ
∇
φ
2+
ρ
gy
The force that the fluid applies to the cylinder, Fc, is
Fc=(p∞−p)ndS =
surface
∫(p∞−p)erBad
θ
θ
=0
θ
=2
π
∫
where B is the length of the cylinder along its axis,
er=excos
θ
+eysin
θ
, and
θ
is an angle
measured from the positive x-axis with its apex at the center of the cylinder. In addition, define
the distance from the center of the cylinder as
R(t)=x−xc(t)
( )
2+y2
so that
cos
θ
=x−xc(t)
( )
R(t)
. Now the potential can be written:
φ
(R,
θ
)=−a2UcR
( )
cos
θ
where R,
θ
,
and Uc are all functions of time for a fixed (x,y) location. Only the unsteady term in the UBE
will contribute a term that involves
dUcdt ≡˙
U
c
, thus:
p∞−p=−
ρ
a2˙
U
cR
( )
cos
θ
+terms leading to no net force
( )
.
Evaluate this one unsteady term on R = a,
p∞−p
( )
R=a=−
ρ
a˙
U
ccos
θ
+…
, and this leads to:
FcB=−
ρ
a2˙
U
ccos
θ
(excos
θ
+eysin
θ
)d
θ
θ
=0
θ
=2
π
∫=−
ρ
a2˙
U
c(
π
ex+0ey)=−
π
a2
ρ
˙
U
cex
So, the apparent mass of the cylinder is equal to the mass of the fluid displaced by the cylinder.
The streamlines for this flow when Uc < 0 are shown in Figure 3.2b.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.49. A stationary sphere of radius a and mass m resides in inviscid fluid with constant
density
ρ
.
a) Determine the buoyancy force on the sphere when gravity g acts downward.
b) At t = 0, the sphere is released from rest. What is its initial acceleration?
c) What is the sphere’s initial acceleration if it is a bubble in a heavy fluid (i.e. when m → 0)?
Solution 7.49. a) The buoyancy force arises from the static pressure acting on the surface of the
sphere. Choose the spherical coordinate system so that ez points opposite gravity and the
hydrostatic pressure is
p=po−
ρ
gz
. Thus the buoyancy force on sphere will be:
FB=−(p−po)era2sin
θ
d
θ
d
ϕ
0
π
∫
0
2
π
∫=(po−p)excos
ϕ
sin
θ
+eysin
ϕ
sin
θ
+ezcos
θ
( )
a2sin
θ
d
θ
d
ϕ
0
π
∫
0
2
π
∫
Performing the
ϕ
integration eliminates two of the coordinate directions, so
FB=2
π
(+
ρ
gz)eza2cos
θ
sin
θ
d
θ
0
π
∫=2
πρ
ga3ezcos2
θ
sin
θ
d
θ
0
π
∫
,
where
p−po=−
ρ
gz
, and z = acos
θ
have been used. The
θ
-integration is completed via a
straightforward change of variable:
FB= +2
πρ
ga3ezcos2
θ
sin
θ
d
θ
0
π
∫=−2
πρ
ga3ez
β
2d
β
1
−1
∫= + 4
3
πρ
ga3ez
.
b) Newton’s second law for the sphere will be:
FB−mgez=(m+madded )dus
dt
, where madded is 1/2
the mass of the displaced fluid. Thus,
dus
dt =FB−mgez
m+madded
=(4 /3)
ρ
a3g−mg
m+2 /3
( )
ρ
a3ez=(4 /3)
ρ
a3−m
2 /3
( )
ρ
a3+mgez
c) If m → 0, then
dus
dt =2gez
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.50. A sphere of mass m and volume V is attached to the end of a light thin flexible
cable of length L. In vacuum, with gravity g acting, the natural frequencies for small longitudinal
(bouncing) and transverse (pendulum) oscillations of the sphere are
ω
b and
ω
p. Ignore the effects
of viscosity, and estimate these natural frequencies when the same sphere and cable are
submerged in water with density
ρ
w. What is
ω
p when
m<<
ρ
wV
?
Solution 7.50. For the longitudinal (bouncing) vibrations, the natural frequency will be
determined from the simple linear differential equation:
Md2z
dt 2+
σ
z=0
where z is the coordinate
of the sphere’s center of mass in longitudinal direction, and
σ
is the extensional stiffness of the
cable. In a vacuum, there will be no fluid dynamic effects so the longitudinal natural frequency
is
ω
b=
σ
M
. When the sphere is placed in water, it will have added mass equal to one half the
mass of the displaced fluid, so that small longitudinal oscillations will follow:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.51. Determine the ideal-flow force on a stationary sphere for the following unsteady
flow conditions.
a) The free stream of velocity Uez is constant but the sphere’s radius a(t) varies.
b) The free stream velocity magnitude changes, U(t)ez, but the sphere’s radius a is constant.
c) The free stream velocity changes direction U(excosΩt+ eysinΩt), but its magnitude U and the
sphere’s radius a are constant.
Solution 7.51. a) The potential for a stationary sphere with a constant radius in a uniform flow
parallel to the z-axis is given by (7.85):
φ
=Ur 1+a3
2r3
#
$
%
&
‘
(
cos
θ
.
When the sphere’s radius varies, a time dependent source term proportional to 1/r must be added
to this potential to produce the requisite radial velocity at r = a. The strength of this source term
is Q = 4πa2(da/dt), thus the appropriate time dependent potential for this situation is:
φ
=Ur 1+a3
2r3
#
$
%
&
‘
(
cos
θ
−a2
r
da
dt
, so
∂φ
∂
t=3
2
Ua2
r2
$
%
&
‘
(
)
da
dt
cos
θ
−2a
r
da
dt
$
%
& ‘
(
)
2
−a2
r
d2a
dt 2
,
∂φ
∂
z=uz=U1+a3
2r3
$
%
&
‘
(
) −3
2
Ua3z2
r5+a2z
r3
da
dt =U1+a3
2r31−3cos2
θ
( )
$
%
&
‘
(
) +a2
r2
da
dt
cos
θ
,
∂φ
∂
r=ur=U1−a3
r3
%
&
‘
(
)
*
cos
θ
+a2
r2
da
dt
and
1
r
∂φ
∂θ
=u
θ
=−U1+a3
2r3
&
‘
(
)
*
+
sin
θ
.
Now consider a CV that encloses the sphere and expands and contracts with it. In this
case, the control surface velocity will be b = (da/dt)er. The integral momentum equation (4.17)
becomes:
d
dt
ρ
udV
CV
∫+
ρ
u(u−b)⋅ndA
CS
∫=d
dt
ρ
udV
CV
∫+
ρ
uur−da
dt
&
‘
( )
*
+
dA
CS
∫=−p
CS
∫erdA +Fs
.
Here the control surface is spherical so n = er, the flux integral is zero because ur = da/dt on the
control surface (r = a), and Fs is an externally applied force that holds the sphere stationary. The
ideal flow force on the sphere, FIF, will be equal and opposite to Fs so
FIF =−Fs=−p
[ ]
r=aera2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫−d
dt
ρ
ur2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫
r=0
a
∫dr
.
From the symmetry of the flow, the only non-zero force component is in the z-direction:
FIF
( )
z=ez⋅FIF =−p
[ ]
r=acos
θ
a2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫−d
dt
ρ
uzr2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫
r=0
a
∫dr
.
The pressure is obtained from the unsteady Bernoulli equation:
ρ∂φ
∂
t+1
2
ρ
∇
φ
2+p=p∞+1
2
ρ
U2
, or
p=p∞+1
2
ρ
U2− ∇
φ
2
( )
−
ρ∂φ
∂
t
.
On r = a this simplifies to:
p
[ ]
r=a=p∞+1
2
ρ
U2−da
dt
%
&
‘ (
)
*
2
−9
4U2sin2
θ
%
&
‘
‘
(
)
*
* −
ρ
3
2Uda
dt
cos
θ
−2da
dt
%
&
‘ (
)
*
2
−ad2a
dt2
%
&
‘
‘
(
)
*
*
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
This can be rearranged into terms that do not lead to a net force, those in [,]-brackets below, and
the one term that does, the final term:
p
[ ]
r=a=p∞+3
2
ρ
da
dt
$
%
& ‘
(
)
2
+1
2
ρ
U21−9
4
sin2
θ
$
%
& ‘
(
) +
ρ
ad2a
dt2
,
–
.
/
0
1
−
ρ
3
2Uda
dt
cos
θ
.
Therefore, the pressure contribution to the ideal-flow force is:
=−2
πρ
d
dt
U
β
+a3
2r3
β
−
β
3
( )
#
$
%&
‘
(+a2
r2
da
dt
β
2
2
)
*
+,
–
.
−1
+1
r=0
a
∫r2dr =−2
πρ
Ud
dt
2
r=0
a
∫r2dr
=−4
π
3
ρ
Ud
dt
a3
( )
=−4
πρ
Ua2da
dt
.
This term represents momentum change that occurs within the sphere.
Combining the pressure and internal-momentum-change forces leads to:
FIF
( )
z=−2
πρ
Ua2da
dt
(sphere internal flow included).
which is a thrust force when da/dt > 0; the sphere is pushed upstream when its radius increases.
In this case, momentum change in the sphere’s interior provides the decisive contribution to the
This time consider a fixed-size CV that encloses the sphere. Use the integral momentum
equation (4.17) to find:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
FIF
( )
z=−p
[ ]
r=acos
θ
a2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫−d
dt
ρ
uzr2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫
r=0
a
∫dr
.
The flux term considered in part a) is zero here because the sphere doesn’t change size; its
surface is motionless (ur = 0 at r = a).
The unsteady term’s contribution to the ideal-flow force is
−d
dt
ρ
uzr2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫
r=0
a
∫dr =−4
π
3
ρ
a3dU
dt
,
and can be obtained by repeating the part a) analysis of this term with a = const. and U = U(t).
such a switch is not necessarily helpful because of the kinematic relationship
u
[ ]
inertial frame =Ω×x+u
[ ]
rotating frame
, where Ω is the angular rotation rate of the rotating frame.
With z-axis vertical, Ω = Ωez, x = (x, y, z), and an inertial-frame velocity of u = U(excosΩt+
eysinΩt), this kinematic relationship becomes:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
where the free stream velocity changes direction,
U=U(excosΩt+eysinΩt)
, and the dipole
strength opposes the free stream and sets the sphere’s diameter,
d=−2
π
Ua3(excosΩt+eysinΩt)
.
Using spherical coordinates,
x=exrcos
ϕ
sin
θ
+eyrsin
ϕ
sin
θ
+ezrcos
θ
, performing the dot
products, and using the two-angle sum formula for the cosine function allows the potential to be
written entirely in terms of scalars:
φ
=U r +a3
2r2
#
$
%
&
‘
(
cos )
ϕ
sin
θ
,
where
ϕ
´ =
ϕ
– Ωt. The radial and angular velocities, and ∂
φ
/∂t are:
∂φ
∂
r=ur=U1−a3
r3
%
&
‘
(
)
*
cos +
ϕ
sin
θ
,
1
r
∂φ
∂θ
=u
θ
=U1+a3
2r3
%
&
‘
(
)
*
cos +
ϕ
cos
θ
,
1
rsin
θ
∂φ
∂ϕ
=u
ϕ
=−U1+a3
2r3
‘
(
)
*
+
,
sin –
ϕ
, and
∂φ
∂
t=ΩU r +a3
2r2
%
&
‘
(
)
*
sin +
ϕ
sin
θ
.
As in parts a) and b), the ideal flow force on the sphere, FIF, can be obtained from a
surface integral of the pressure, and a volume integral over the sphere’s interior.
FIF =−p
[ ]
r=aera2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫−d
dt
ρ
ur2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫
r=0
a
∫dr
.
To evaluate the pressure term, use the Bernoulli equation,
ρ∂φ
∂
t+1
2
ρ
∇
φ
2+p=const.
,
from the stagnation point at r = a,
θ
= π/2, and
ϕ
´ = π to any other point on the surface of the
sphere to find the pressure
p(a,
θ
,#
ϕ
)≡p
[ ]
r=a
on the surface of the sphere:
3
2
ρ
ΩUasin $
ϕ
sin
θ
+1
2
ρ
U29
4cos2$
ϕ
cos2
θ
+sin2$
ϕ
( )
+p(a,
θ
,$
ϕ
)=p(a,
π
/2,
π
)
.
Rearrange this and denote p(a, π/2, π) by ps.
p(a,
θ
,#
ϕ
)=ps−9
8
ρ
U21−cos2#
ϕ
sin2
θ
( )
−3
2
ρ
ΩUasin #
ϕ
sin
θ
.
Only the final term on the right leads to a net pressure force:
−p
[ ]
r=aera2sin
θ
d
ϕ
d
θ
ϕ
=0
2
π
∫
θ
=0
π
∫
=3
2
ρ
ΩUa2sin )
ϕ
sin2
θ
excos
ϕ
sin
θ
+eysin
ϕ
sin
θ
+ezcos
θ
( )
d
ϕ
d
θ
.
ϕ
=0
2
π
∫
θ
=0
π
∫
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.52. Consider the flow field produced by a sphere of radius a that moves in the x–
direction at constant speed U along the x-axis in an unbounded environment of a quiescent ideal
fluid with density
ρ
. The pressure far from the sphere is p∞ and there is no body force. The
velocity potential for this flow field is:
φ
(x,y,z,t)=−a3
U
2
x−Ut
(x−Ut)2+y2+z2
“
#$
%
3 2
.
a) If
u=(u,v,w)
, what is
u(x, 0, 0, t)
, the velocity along the x-axis as a function of time? [Hint:
consider the symmetry of the situation before differentiating in all directions.]
b) What is p(x,0,0,t), the pressure along the x-axis as a
function of time?
c) What is the pressure on the x-axis at x = Ut ± a?
d) If the plane defined by z = h is an impenetrable flat
surface and the sphere executes the same motion, what
additional term should be added to the given potential?
e) Compared to the sphere’s apparent mass in an
unbounded environment, is the sphere’s apparent mass
larger, the same, or smaller when the impenetrable flat
surface is present?
Solution 7.52. a) To save writing let,
r(t)=(x−Ut)2+y2+z2
“
#$
%
1 2
, so
φ
=−a3
U
2
(x−Ut)
r3(t)
.
Compute velocity components from
∇
φ
=
u
. Start with:
u=∂
φ
∂x=−a3
U
2
r2(t)−3(x−Ut)2
r5(t)
#
$
%&
‘
(
,
evaluate this on the x-axis (y = z = 0) where
r(t)=x−Ut
to find:
u(x, 0, 0, t)=a3
U
. Here
φ
x!
y !
z !
h !
x = Ut !
U !
2a !
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
c) At x = Ut ± a the factor in large (,)-parentheses in the part b) result is unity, so p = p∞ +
(1/2)
ρ
U2 at these locations. This answer can also be reached by noting that the specified
locations are stagnation points on the sphere when it is stationary and the flow moves past it.
d) The method of images applies to this situation, so an image sphere must move along the line
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 7.53. In three dimensions, consider a solid object moving with velocity U near the
origin of coordinates in an unbounded quiescent bath of inviscid incompressible fluid with
density
ρ
. The kinetic energy of the moving fluid in this situation is:
KE =1
2
ρ
∇
φ
2
V
∫dV
where
φ
is the velocity potential and V is a control volume that contains all of the moving fluid
but excludes the object. (Such a control volume is shown in the figure for Exercise 7.29 when
A3→0
and U = 0.)
a) Show that
KE =−1
2
ρ φ
∇
φ
⋅n
( )
A
∫dA
where A encloses the body and is coincident with its
surface, and n is the outward normal on A.
b) The apparent mass, M, of the moving body may be defined by
KE =1
2MU2
. Using this
definition, the result of a), and (7.97) with xs = 0, show that M = 2πa3
ρ
/3 for a sphere.
Solution 7.53. Start from the given equation, use the
recommended CV, add
φ
∇2
φ
=0
to the integrand, and apply
Green’s divergence theorem.
KE =
ρ
2
lim
A3→0∇
φ
2
V
∫dV =
ρ
2
lim
A3→0∇
φ
⋅ ∇
φ
( )
V
∫dV
=
ρ
2
lim
A3→0∇
φ
⋅ ∇
φ
+
φ
∇2
φ
( )
V
∫dV =
ρ
2
lim
A3→0∇ ⋅
φ
∇
φ
( )
V
∫dV
=
ρ
2
lim
A3→0
φ
∇
φ
⋅ni
Ai
∫dA
i=1
3
∑
where n1 is the normal on A1, n2 is the normal on A2, and n3 is the normal on A3. When the limit is
taken, the net contribution of A3 is zero because the surface area of A3 goes to zero. This leaves:
KE =
ρ
2
φ
∇
φ
⋅n1
A1
∫dA +
ρ
2
φ
∇
φ
⋅n2
A2
∫dA
,
where n1 points away from the origin on A1 and n2 points inward on A2. By definition, the
volume V enclosed by A1 contains all the moving fluid, thus
∇
φ
⋅n1=u⋅n1=0
on A1, so the first
integral in the last equation is equal to zero. Now define the outward normal on A2 as n = – n2,
and drop the subscript from the body-conforming surface A2 to reach:
KE =−
ρ
2
φ
∇
φ
⋅n
A
∫dA
.
b) The potential for a sphere of radius a moving at velocity U that is instantaneously centered at
the origin of a spherical coordinate system is:
φ
=−a3
2r3U⋅x=−a3
2r2Ucos
θ
,
where the second equality follows when the direction of the z-axis is chosen to coincide with the
sphere’s velocity at the moment of interest. For a sphere, n = er and surface area element is dA =
a2sin
θ
d
θ
d
ϕ
, so the kinetic energy integral becomes:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling