Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
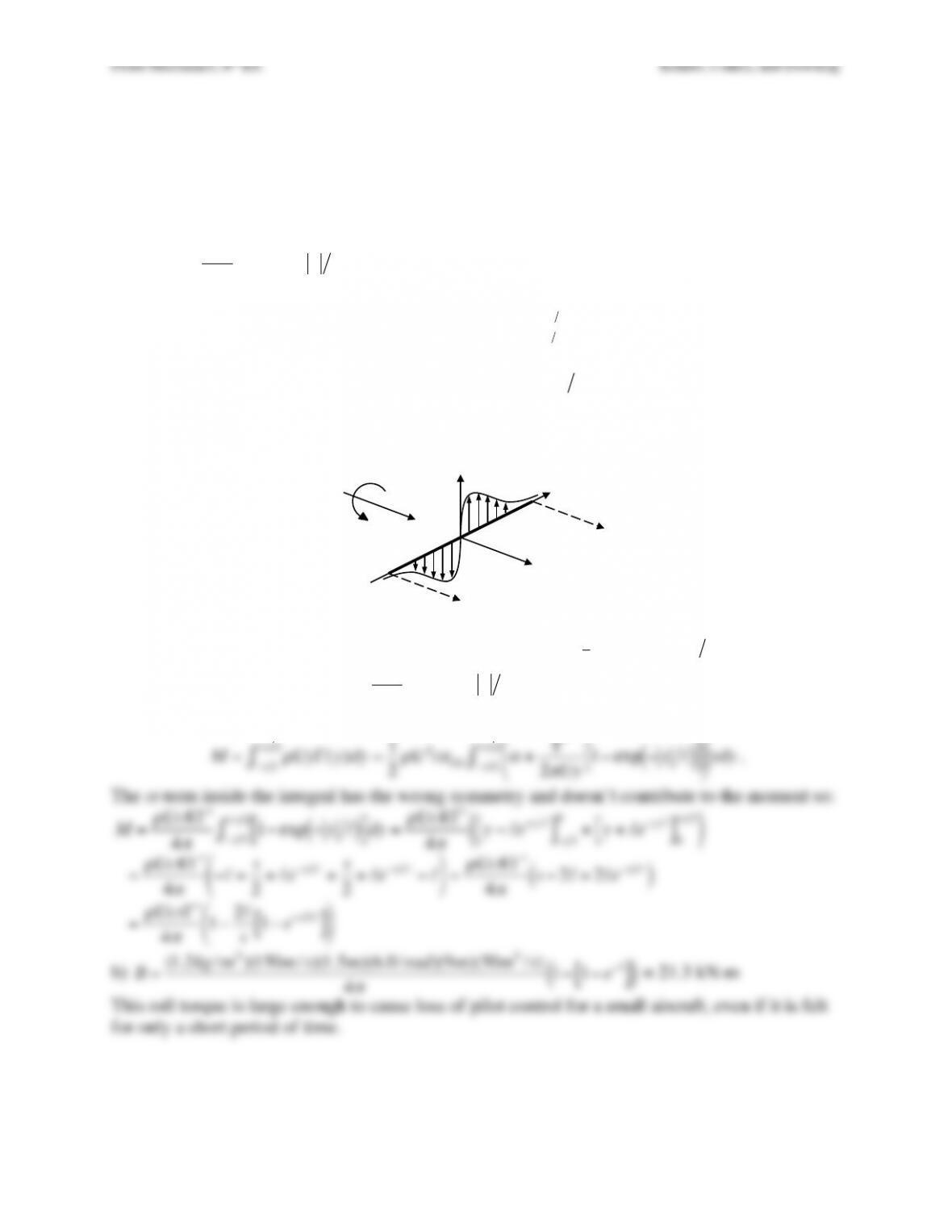
Exercise 14.10. A thin Zhukhovsky airfoil has a lift coefficient of 0.3 at zero incidence. What is
the lift coefficient at 5° incidence?
Solution 14.10. From (14.12), the lift coefficient of a Zhukhovsky airfoil is:
CL=2
π
(
α
+
β
)
.
If CL = 0.3 when
α
= 0, then
β
= 0.3/2π. Therefore when
α
= 5°,
CL=2
π
5°
180°
π
+0.3
2
π
#
$
% &
‘
( =0.848
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.11. The simplest representation of a three-dimensional aircraft wing in flight is the
rectangular horseshoe vortex.
a) Calculate the induced downwash at the center of the wing.
b) Assuming the result of part a) applies along the entire wingspan, estimate
CDi
, the lift-induced
coefficient of drag, in terms of the wing’s aspect ratio: AR = s2/A, and the wing’s coefficient of
lift
CL=L1
2
ρ
U2A
( )
, where A is the planform area of the wing.
c) Explain why the result of part b) appears to surpass the performance of the optimal elliptic lift
distribution.
Solution 14.11. a) Use the result of exercise 14.10. For the rectangular horseshoe vortex, each of
the trailing vortices induces a vertical velocity of
w=−Γ
4
π
(b/2) cos90°−cos180°
( )
=−Γ
2
π
b
.
Thus, the total downwash velocity will be twice this:
wtotal =−Γ
π
b
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.12. The circulation across the span of a wing follows the parabolic law
Γ=Γ01−2y s
( )
2
( )
. Calculate the induced velocity w at midspan, and compare the value with
that obtained when the distribution is elliptic.
Solution 14.12. From
Γ=Γ01−2y s
( )
2
( )
, determine
dΓ
dy =−8Γ0y s2
. Then, from (14.13)
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.13. An untwisted elliptic wing of 20-m span supports a weight of 80,000 N in a
level flight at 300 km/hr. Assuming sea level conditions, find (i) the induced drag and (ii) the
circulation around sections halfway along each wing.
Solution 14.13. (i) An untwisted wing with an elliptic area is expected to have an elliptic
circulation distribution. The induce drag in this case is given by (14.25):
Di=2L2
πρ
U2s2=2(8 ×104N)2
π
(1.2kgm−3)(83.3ms−1)2(20m)2=1.22kN
,
where 300 km/hr has been converted to 83.3 m/s.
(ii) Also from (14.25), the maximum circulation Γ1 is
Di=
π
8
ρ
Γ
1
2
and this implies
Γ
1=8Di
ρπ
=8(1.22 ×103N)
π
(1.2kgm−3)=50.9m2s−1
.
Halfway along each wing:
Γ(±s/4) =Γ
11−2(±s/4)
s
$
%
& ‘
(
)
2
$
%
&
&
‘
(
)
)
1 2
=50.9 m2
s1−1
2
$
%
& ‘
(
)
2
$
%
&
&
‘
(
)
)
1 2
=44.1 m2
s
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.14 . A wing with a rectangular planform (span = s, chord = c) and uniform airfoil
section without camber is twisted so that its geometrical angle,
α
w, decreases from
α
r at the root
(y = 0) to zero at the wing tips (y = ± s/2) according to the distribution:
α
w(y)=
α
r1−2y s
( )
2
.
a) At what global angle of attack,
α
t, should this wing be flown so that it has an elliptical lift
distribution? The local angle of attack at any location along the span will be
α
t +
α
w. Assume the
two-dimensional lift curve slope of the foil section is K.
b) Evaluate the lift and the lift-induced drag forces on the wing at the angle of attack determined
in part a) when:
α
r = 2°, K = 5.8 rad.–1, c = 1.5 m, s = 9 m, the air density is 1 kg/m3, and the
airspeed is 150 m/s
Solution 14.14. a) For an elliptical lift distribution without camber (
β
= 0), only the first two
terms of the finite wing lifting line equation (14.20) are needed:
K
2
Uc
α
=1+cKn
4ssin
γ
$
%
&
‘
(
)
n=1
∞
∑Γnsin(n
γ
)
.
The first two terms of this non-traditional Fourier series “solution” are obtained by matching the
left side of the equation to the right side evaluated at n = 1.
K
2
Uc
α
=1+cK
4ssin
γ
$
%
&
‘
(
)
Γ
1sin(
γ
)=Γ
1sin(
γ
)+cK
4sΓ
1
For the wing twist specified in the problem statement,
α
=
α
t+
α
w=
α
t+
α
r1−2y s
( )
2
. Now,
switch to the angle coordinate,
y=−s2
( )
cos
γ
, of the lifting line equation so that
α
=
α
t+
α
rsin
γ
, and plug this into the last equation:
K
2
Uc
α
t+
α
rsin(
γ
)
( )
=Γ
1sin(
γ
)+cK
4sΓ
1
.
Require equality of the constant and sin
γ
terms on both sides of the equation:
K
2
Uc
α
t= + cK
4sΓ
1
, and
K
2
Uc
α
r=Γ
1
.
Eliminate Γ1 and solve for
α
t;
α
t=Kc
α
r(4s)
. Note that this angle is positive so the wing must
be pitched slightly upward. For the parameters given in part b) the value of
α
t is 0.48°.
b) The lift will be:
L=
π
s
4
ρ
UΓ
1=
π
sc
8
ρ
U2K
α
r
, so
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.15. Consider the wing shown in Figure 14.25. If the foil section is uniform along the
span and the wing is not twisted, show that the three-dimensional lift coefficient, CL,3D is related
to the two-dimensional lift coefficient of the foil section, CL,2D, by:
CL,3D=CL,2D1+2Λ
( )
,
where Λ = s2/A is the aspect ratio of the wing.
Solution 14.15. The wing shown in Figure 14.24 has an elliptical planform. Thus, with a uniform
foil section and no twist, it will have an elliptical lift distribution and constant downwash w. The
lift force L3D of the three-dimensional wing can be calculated in terms of an integral of the
circulation Γ(y) at each span location y. Starting from (14.15) and (14.17) with
β
= 0, this is:
L3D=
ρ
UΓ(y)dy
−s2
+s2
∫=K
2
ρ
U2c(y)
α
−w
U
‘
(
) *
+
,
dy
−s2
+s2
∫=K
2
ρ
U2
α
−w
U
‘
(
) *
+
, c(y)dy
−s2
+s2
∫=K
2
ρ
U2
α
−w
U
‘
(
) *
+
,
A
.
The final two equalities follow because the downwash velocity w is constant for an elliptical lift
distribution, and the integral of the cord c(y) over the span is the planform area A. The two ends
of this extended equality imply:
CL,3D=L3D
1 2
( )
ρ
U2A=K
α
−w
U
%
&
‘ (
)
*
. (&)
Here, the downwash velocity is given by (14.24), w = Γ1/2s, and Γ1 is related to the total lift force
L3D of the three-dimensional wing by (14.21):
L3D=
π
s
4
ρ
UΓ
1
.
Therefore (&) becomes:
CL,3 D=K
α
−1
2sU
4L3D
π
s
ρ
U
&
‘
(
)
*
+ =K
α
−A
π
s2
L3D
1 2
( )
ρ
U2A
&
‘
(
)
*
+ =K
α
−1
π
ΛCL,3 D
&
‘
( )
*
+
,
where Λ = s2/A is the wing’s aspect ratio. Solving for CL,3D produces:
CL,3D=K
α
1+K
π
Λ
( )
≅CL,2D
1+2
π π
Λ
( )
=CL,2D
1+2Λ
( )
,
where the angle of attack
α
is measured from the zero-lift orientation of the wing, and the second
equality is approximate because the foil section’s two-dimensional lift-curve slope K in viscous
flow may be a little smaller than its inviscid value K = 2
π
.
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.16. The wing-tip vortices from large heavy aircraft can cause a disruptive rolling
torque on smaller lighter ones. Lifting line theory allows the roll torque to be estimated when the
small airplane’s wing is modeled as a single linear vortex with strength
Γ(y)
that resides at x = 0
between y = –s/2 and y = +s/2. Here, the small airplane’s wing will be presumed rectangular
(span s, chord c) with constant foil-shape, and the trailing vortex from the heavy airplane’s wing
will be assumed to lie along the x-axis and produce a vertical velocity distribution at x = 0 given
by:
w(y)=“
Γ
2
π
y1−exp −y
( )
[ ]
. To simplify your work for the following items, ignore the
trailing vortices (shown as dashed lines) from the small airplane’s wing and assume U >> w.
a) Determine a formula for the rolling moment,
M=
ρ
UyΓ(y)dy
−s2
+s2
∫
, on the small aircraft’s
wing in terms of Γ´, s, c, , the air density
ρ
, the flight speed of the small aircraft U, and the lift-
curve slope of the small aircraft’s wing section
K=dCL,2Dd
α
, where
α
is the small-aircraft-
wing angle of attack.
b) Calculate M when
ρ
= 1.2 kg/m3, U = 150 m/s, K = 6.0/rad, b = 9 m, c = 1.5 m, Γ´ = 50 m2/s,
and s/(2
) = 1. Comment on the magnitude of this torque.
Solution 14.16. a) Use the second lifting line equation,
Γ(y)=1
2UcK
α
+w(y)U
( )
, and the
specified vertical velocity,
w(y)=“
Γ
2
π
y1−exp −y
( )
[ ]
to determine the roll torque on the small
aircraft’s wing:
M=
ρ
UyΓ(y)dy
−s2
+s2
∫=1
2
ρ
U2ca2D
α
+‘
Γ
2
π
Uy 1−exp −y
( )
[ ]
)
*
+
,
–
.
ydy
−s2
+s2
∫
.
The
α
-term inside the integral has the wrong symmetry and doesn’t contribute to the moment so:
M=
ρ
UcK #
Γ
4
π
1−exp −y
( )
[ ]
dy
−s2
+s2
∫=
ρ
UcK #
Γ
4
π
y−e+y
[ ]
−s2
0+y+e−y
[ ]
0
+s2
( )
=
ρ
UcK #
Γ
4
π
−+s
2+e−s2+s
2+e−s2−
‘
(
) *
+
, =
ρ
UcK #
Γ
4
π
s−2+2e−s2
( )
=
ρ
Ucs #
Γ
4
π
1−2
s
1−e−s2
[ ]
‘
(
) *
+
,
b)
B=(1.2kg /m3)(150m/s)(1.5m)(6.0 /rad)(9m)(50m2/s)
4
π
1−1−e−1
[ ]
( )
= 21.3 kN-m
This roll torque is large enough to cause loss of pilot control for a small aircraft, even if it is felt
for only a short period of time.
w(y)!y!
x!
z!
U
!´!
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.17. Consider the ideal rectilinear horseshoe vortex of a simple wing having span s.
Use the (x, y, z) coordinates shown for the following items.
a) Determine a formula for the induced vertical velocity w at (x, y, 0) for x > 0 and y > 0.
b) Using the results of part a), evaluate the induced vertical velocity at the following three
locations (s, 0, 0), (0, s, 0), and (s, s, 0)
c) Imagine that you are an efficiency-minded migrating bird and that the rectilinear horseshoe
vortex shown is produced by another member of your flock. Describe where you would choose
to center your own wings. List the coordinates of the part b) location that is closest to your
chosen location.
Solution 14.17. The induced vertical velocity w at (x, y, 0) for x > 0 and y > 0 will be the result
of the sum of the induced velocities from (1) the port-side vortex located at y = –s/2, (2) the
bound vortex of the wing located at x = 0, and (3) the starboard-side vortex located at y = +s/2.
All three vortices have strength Γ. Using the angles in the planform drawing provided. The sum
of induced velocity from vortices (1) and (2) and (3) is:
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.18. As an airplane lands, the presence of the ground changes the plane’s
aerodynamic performance. To address the essential features of this situation, consider uniform
flow past a horseshoe vortex (heavy solid lines below) with wingspan b located a distance h
above a large flat boundary defined by z = 0. From the method of images, the presence of the
boundary can be accounted for by an image horseshoe vortex (heavy dashed lines below) of
opposite strength located a distance h below the boundary.
a) Determine the direction and the magnitude of the induced velocity at x = (0, 0, h), the center
of the wing.
b) Assuming the result of part a) applies along the entire wingspan, estimate L and
Di
, the lift
and lift-induced drag, respectively, in terms of b, h, Γ, and
ρ
= fluid density.
c) Compare the result of part b) to that obtained for the horseshoe vortex without a large flat
surface:
L=
ρ
UΓb
and
Di=
ρ
Γ2
π
. Which configuration has more lift? Which one has less
drag? Why?
Solution 14.18. a) Five vortices will contribute to the induced velocity at
x=(0,0,h)
. Number
these as follows:
1 = starboard wingtip vortex
2 = starboard wingtip image vortex
3 = port wingtip vortex
4 = port wingtip image vortex
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
u2=Γ
ez
b/2
2h
$
&
‘
)
The sum of these five terms is:
utotal =−Γez
π
b+Γ
2
π
(b/2)2+4h2
ez
b/2
(b/2)2+4h2
%
&
‘
‘
(
)
*
*
−Γex
2
π
(2h)
b/2
(b/2)2+4h2
utotal =−Γ
4h2
%
&
(
)
ez−Γ
b/2
ex=−uzez−uxex
b) The lift force will be:
L=
ρ
U−wx
( )
Γb
, and the induced drag force will be:
Di=L
ε
=
ρ
U−wx
( )
Γbwz
U−wx
=
ρ
Γbwz=
ρ
Γ2
π
4h2
(b/2)2+4h2
‘
(
)
*
+
,
Note, that as h/b → 0, the induced drag disappears.
c) For constant speed flight close to the ground surface, there is less lift and less drag for a fixed
value of Γ. The lowering of the lift occurs because the induced velocity from the main wing’s
image vortex slows the on-coming stream at the location of the real wing. The induced drag is
lower because the image tip vortices produce upwash that partially counter acts the downwash
unexpectedly long period of time before touching down. This apparent delay in touching down is
merely the time necessary for pilot to adjust the aircraft’s trim to continue its decent while flying
in ground effect. [Spoilers are flaps on the top of the wing that spoil the airflow on the suction
side of the wing; they are used to increase form drag and reduce lift in a controlled manner.]
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.19. Before modifications, an ordinary commercial airliner with wingspan s = 30 m
generates two tip vortices of equal and opposite circulation having Rankine velocity profiles (see
(3.28)) and a core size
σ
o = 0.5 m for test-flight conditions. The addition of wing-tip treatments
(sometimes known as winglets) to both of the aircraft’s wing tips doubles the tip vortex core size
at the test condition. If the aircraft’s weight is negligibly affected by the change, has the lift-
induced drag of the aircraft been increased or decreased? Justify your answer. Estimate the
percentage change in the induced drag.
Solution 14.19. For the conditions stated, the lift-induced drag of the aircraft has decreased by
the addition of winglets. This contention is supported by an approximate analysis of the kinetic
energy of the vortex flow behind the aircraft.
In an unbounded nominally-quiescent fluid medium, an increase in length dl of a single
semi-infinite line vortex increases the kinetic energy of the fluid by, dKE, where:
dKE =1
2
ρ
u
θ
22
π
rdr
0
∞
∫
[ ]
dl
.
A Rankine vortex is defined by:
u
θ
(r)=Γ2
πσ
2
( )
r for r≤
σ
Γ2
π
r for r>
σ
‘
(
)
*
+
,
where
σ
is the core size, and r is the distance perpendicular to the vortex axis. Thus, the kinetic
energy increment for Rankine vortex is:
dKE =1
2
ρ
Γ
2
πσ
2
&
‘
( )
*
+
2
0
σ
∫r22
π
rdr +lim
R→∞
Γ
2
π
r
&
‘
( )
*
+
2
σ
R
∫2
π
rdr
/
0
1
2
3
4
dl
.
The upper limit of the second integral is problematic for a single vortex. However, the airliner
will have two wing-tip vortices of equal and opposite sign so evaluation of the limit is not
necessary at this point.
Performing the two integrations yields:
dKE =1
2
ρ
Γ2
2
π
1
σ
4r3
0
σ
∫dr +lim
R→∞
1
r
σ
R
∫dr
)
*
+
,
–
.
dl =
ρ
Γ2
4
π
1
σ
4
σ
4
4+lim
R→∞
ln r
( )
σ
R
)
*
+
,
–
.
dl
=
ρ
Γ2
4
π
1
4+lim
R→∞
ln R
( )
−ln
σ
)
*
+
,
–
.
dl
.
Use the final part of this equality, divide by the time increment dt, and recognize dl/dt = U = the
aircraft’s velocity, to find:
dKE
dt =
ρ
Γ2U
4
π
1
4+lim
R→∞
ln R
( )
−ln
σ
)
*
+
,
–
.
.
For an aircraft that produces two counter rotating tip vortices, we can write the following
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Fluid Mechanics, 6th Ed. Kundu, Cohen, and Dowling
Exercise 14.20. Determine a formula for the range, R, of a long-haul jet-engine aircraft in steady
level flight at speed U in terms of: MF = the initial mass of usable fuel; MA = the mass of the
airframe, crew, passengers, cargo, and reserve fuel; CL/CD = the aircraft’s lift–to-drag ratio; g =
the acceleration of gravity; and
η
= the aircraft’s propulsion system thrust-specific fuel
consumption (with units of time/length) defined by: dMF/dt = –
η
D, where D = the aircraft’s
aerodynamic drag. For simplicity, assume that U, the ratio CL/CD, and
η
are constants. [Hints. If
M(t) is the instantaneous mass of the flying aircraft, then L = Lift = Mg, M = MF + MA, and dM/dt
= dMF/dt. The final formula is known as the Breguet range equation.]
Solution 14.20. For steady level flight, an aircraft’s engine thrust T will equal its drag D. Thus,
the beginning equation is:
dM
dt =dM f
dt =−
η
D
.
Use the two ends of this extended equality, and divide on the left by M and on the right by L/g.
This leads to:
1
M
dM
dt =−
η
Dg
L=−1
CLCD
g
η
.
Separate the differential on the left and recognize that Udt = ds = an element of path length along
the flight:
1
M
MF+MA
MA
∫dM =−1
CLCD
g
η
UU dt
0
t
∫=−1
CLCD
g
η
Uds
0
R
∫
,
where t is the time of steady level flight and R is the range of the flight. Perform the integrations
to find:
ln MA
MA+MF
!
“
#$
%
&=−1
CLCD
g
η
UR
.
Solve for R to reach the final form:
R=U CLCD
( )
g
η
ln 1+MF
MA
!
“
#$
%
&
.
Interestingly, air density does not explicitly enter this formula. Plus, the apparent proportionality
between R and U may be somewhat misleading. The aircraft’s lift must balance its weight so
higher U must be paired with lower CL, and lower U must be paired with higher CL. Plus, CD
tends to increase with increasing CL, too (see Figure 14.28), so maximizing the range of a jet
engine aircraft means achieving a high lift-to-drag ratio at high speed.