CHAPTER 8
8.1 Prepare a little Monte Carlo code that integrates I(z)=Rb
af(z,x)dx. Apply your code to a few simple integrals,
plus
si(z)=−Zπ/2
0
e−zcos xcos(zsin x)dx =Si(z)−π
2.
Note: Si(1) =0.94608.
A=0.
B=1.570796
WRITE(*,*) ’INPUT # OF BUNDLES’
FINT=0.
DO I=1,NBUNDLS
X=A+(B-A)*RAN1(ISEED)
END
0.95
0.96
0.97
0.98
242 RADIATIVE HEAT TRANSFER
8.2 In a Monte Carlo simulation involving the plate of Problem 3.9 but of finite width w, a photon bundle is to be
emitted from the plate with a wavelength of λ=2µm. Find the emission point and direction of this photon
bundle in terms of random numbers.
CHAPTER 8 243
8.3
w
w
A triangular, isothermal surface as shown has the following spectral emittance:
ǫλ=
0.1, λ < 2µm; θ≤60◦
0.6, λ > 2µm; θ≤60◦
0.0,all λ;θ > 60◦
For a Monte Carlo simulation
(a) find a point of bundle emission in terms of random numbers,
(b) find a wavelength of bundle emission in terms of random numbers,
(c) find a direction of bundle emission in terms of random numbers.
=0.6f(λT)−0.5f(λcT)λ>λc
0.6−0.5f(λcT), λ < λc,
0.6−0.5f(λcT), λ > λc,
CHAPTER 8 245
8.4 A semicircular disk as shown has a temperature distribution given by T(r)=
T0/1+(r/R)2, and its emittance is gray and nondiffuse with
ǫ′=ǫ′
λ(λ, θ, ψ)=(0.6, 0 ≤θ≤30◦,
0, θ > 30◦.
For a Monte Carlo simulation
(a) find a point of emission in terms of random numbers,
(b) find a direction of emission in terms of random numbers. You may leave your answer in simple implicit
form.
246 RADIATIVE HEAT TRANSFER
8.5 A light pipe with direct solar irradiation is to be investigated via a Monte Carlo method. Such a device consists
of a straight or curved tube covered with a highly-reflective material to pipe light into a room. At visible
wavelengths the reflectance from the pipe wall is ρ′
λ(θout)=1.5ρλcos θout, with reflection angle θout measured
from the local surface normal, and visible light intensity due to direct sunshine may be approximated by
Lλ=KλIλ,sun =Cexp[−A2(λ−λ0)2], λ0=0.56µm,A=20/µm.
(a) Find the pertinent relationship to determine wavelengths of emission as a function of random number.
(b) Find an expression for reflection angle vs. random number.
(a)
CHAPTER 8 247
8.6 At the Aaronsburg (Pennsylvania) Apple Fest you have won a large piece of el-
derberry pie (yumh!) as shown. The wheels in the oven must have been spinning,
because it appears that the number of elderberries per unit area increases lin-
early proportional with radius! If there are 1000 elderberries otherwise randomly
distributed on the slice, make a scatter plot of elderberries on the pie slice.
x
y
0 5 10 15 20
0
5
10
15 1000 berri
x
y
0 5 10 15 20
0
5
10
15 1000 berries
uniform dist
248 RADIATIVE HEAT TRANSFER
8.7 Consider a black disk 0 ≤r≤Rwith temperature distribution T4(r)=T4
0e−C(r/R)2. Develop the random
number relations for points of emission; draw random numbers for 1000 emission points and draw them in
a scattergram for the cases of C=0 and C=5. Use R=10 cm.
CE=1.-exp(-C)
DO i=1,NB
!
! point of emission
!
IF(CE>0.) THEN
8.8 A disk of radius Ris opposed by a square plate (sides of length R) parallel to it, and a distance Raway. Find
the view factor from disk to square plate. Use 100,000 bundles, plotting updated results after every 5,000
bundles.
F=0.
!
! break up into 20 samples
!
nout=NB/20
DO i=1,20
DO j=1,nout
!
sy=sint*sin(psi)
sz=sqrt(1-sint2)
!
! photon distance to square, check x,y-coordinates there
!
d=R/sz
250 RADIATIVE HEAT TRANSFER
CHAPTER 8 251
8.9 Consider two infinitely long parallel plates of width wspaced a distance hapart (see Configuration 32) in
Appendix D).
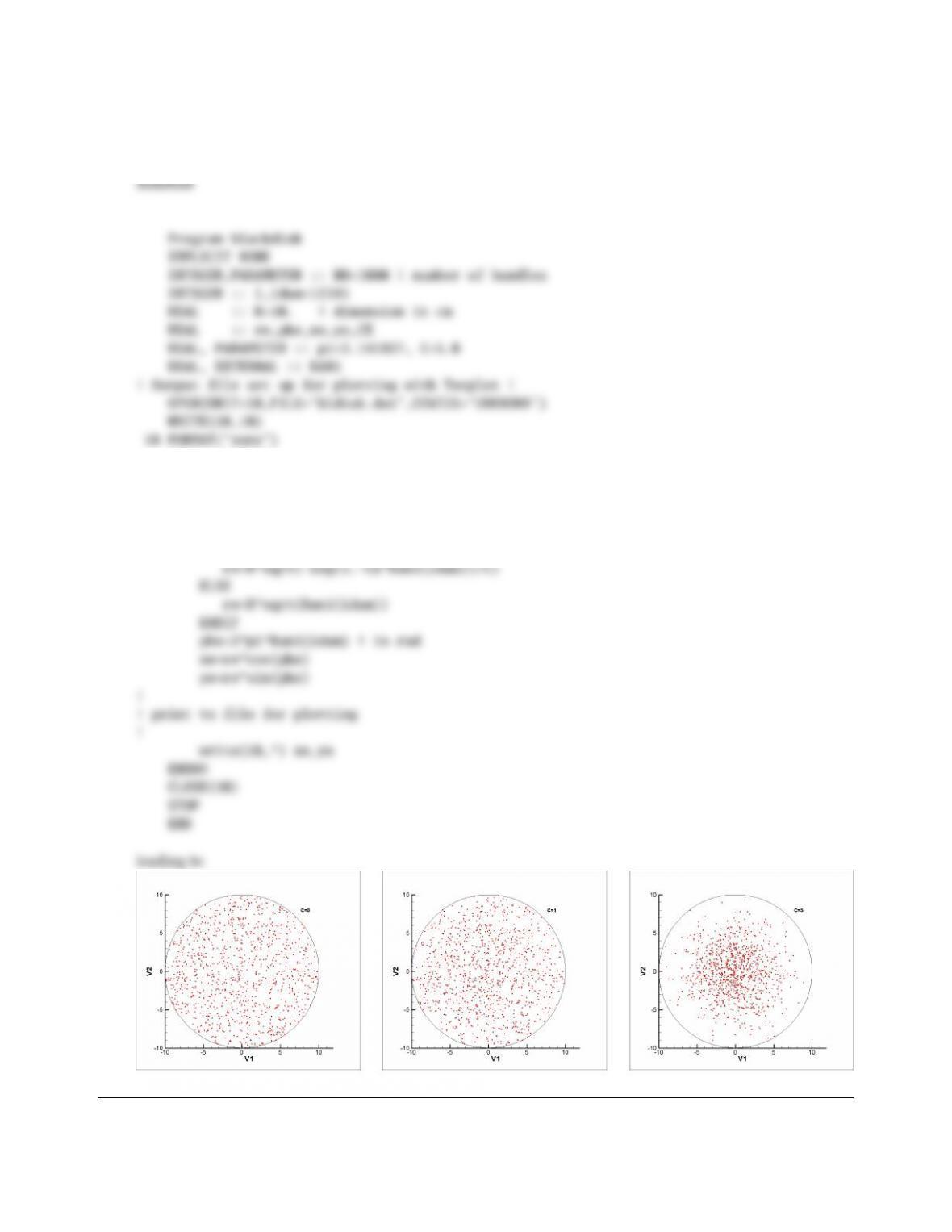
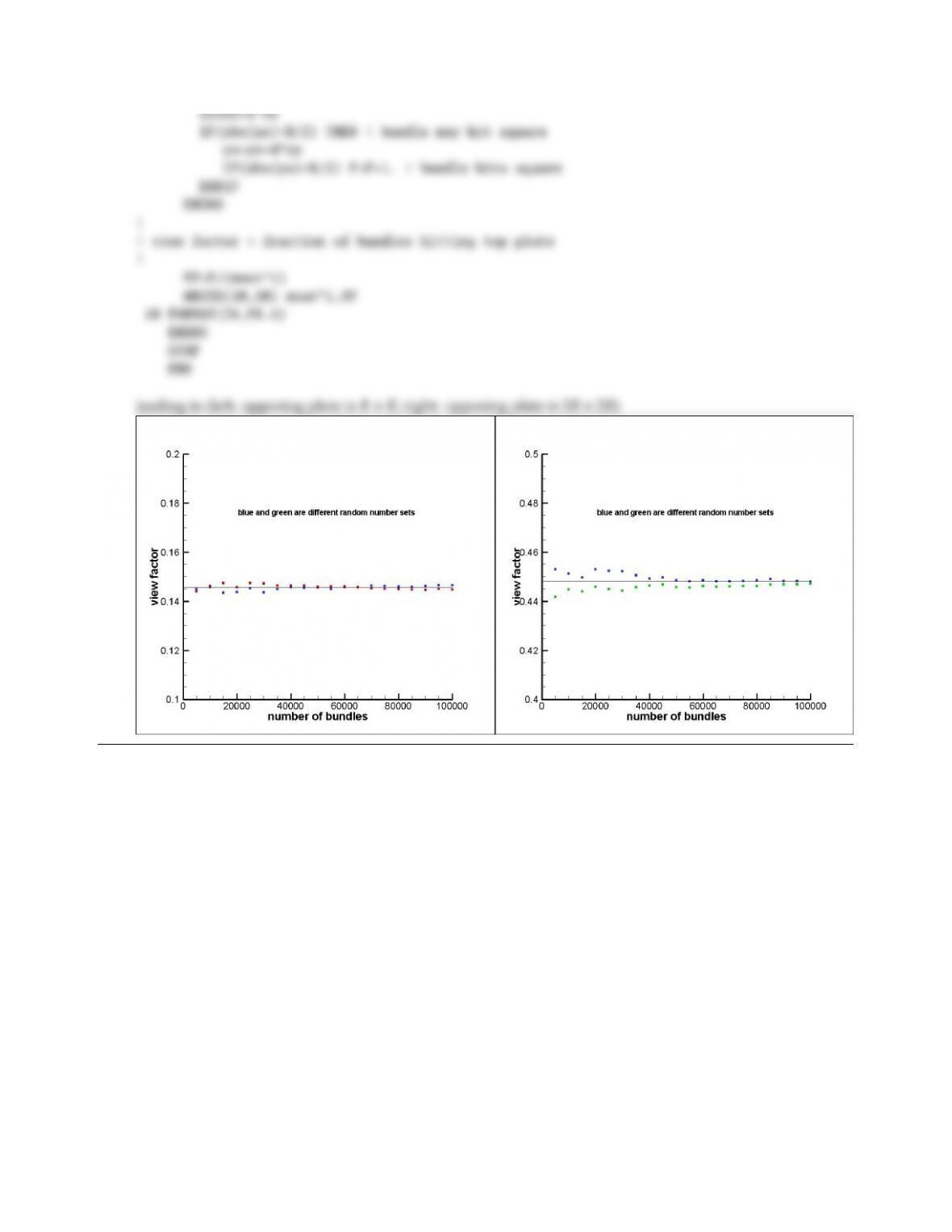
(a) Calculate F1−2via Monte Carlo for the case that the top plate is horizontally displaced by a distance L. Use
L=h=w.
(b) Calculate Fs
1−2via Monte Carlo for the case that both plates are specular (with identical reflectances
ρs
1=ρs
2=0.5), but not horizontally displaced. Use L=0; h=w.
Prepare a figure similar to Fig. 8-2, also including analytical results for comparison.
PI=4.*ATAN(1.)
! SET LENGTHS, EMISSIVITIES
EPS2=0.5 ! assumed diffuse
WW=1. ! width of plates
HH=1. ! distance between plates
!
! EXACT VIEW FACTOR (FOR ABOVE AL,WW,HH)
!F12EX=(.5*(SQRT((AL+WW)**2+HH**2)+SQRT((AL-WW)**2+HH**2))-SQRT(AL**2+HH**2))/WW
!WRITE(*,*) ’INPUT # OF BUNDLES’
PSI=2.*PI*RAN1(ISEED) ! azimuthal angle of emission
COSPS=COS(PSI)
SINPS=SIN(PSI)
SINSQTH=RAN1(ISEED) ! sinˆ2 of polar angle of emission
NNOW=100.*K
WRITE(LU,2000) NNOW,F12/NNOW,F12EX
1000 CONTINUE
2000 FORMAT(I6,2E12.4)
STOP
END
EPS1=0.5 ! assumed specular
AL=0. ! horizontal displacement of plates (here = 0)
HH=1. ! distance between plates
!
! EXACT VIEW FACTORS (FOR ABOVE AL,WW,HH)
!N=0
10 N=N+1
F(N)=SQRT(1.+N*N)-N