CHAPTER 5
5.1
Tsky
fire
ground
h
4
4
4
3
2
1
A fire fighter (approximated by a two-sided black surface at
310 K 180 cm long and 40 cm wide) is facing a large fire at a dis-
tance of 10 m (approximated by a semi-infinite black surface at
1500 K). Ground and sky are at 0◦C (and may also be approx-
imated as black). What are the net radiative heat fluxes on the
front and back of the fire fighter? Compare these with heat rates
by free convection (h=10 W/m2K, Tamb =0◦C).
=0.5446,
F1−4=1−F13 =0.4554.
=1.8×0.4×5.670 ×10−83104−15004×0.5446−2734×0.4554
Q1=−112 kW
Q2=1.8×0.4×5.670 ×10−8(3104−2734)=150 W
For comparison, for free convection
Q1=Q2=Ah(Tman −Tamb)=1.8×0.4×10 ×(310−273) =266 W
CHAPTER 5 101
5.2
T3 = 500 K
q2 = 0
A small furnace consists of a cylindrical, black-walled enclosure, 20 cm long and
with a diameter of 10 cm. The bottom surface is electrically heated to 1500 K,
while the cylindrical sidewall is insulated. The top plate is exposed to the envi-
ronment, such that its temperature is 500 K. Estimate the heating requirements
for the bottom wall, and the temperature of the cylindrical sidewall, by treating
the sidewall as (a) a single zone, (b) two equal rings of 10 cm height each.
0.252=18
q1=5.670 ×10−8h15004−12654×0.9443−5004×0.0557i=1.4965 ×105W
m2
and
Q1=πr2q1=π×0.052×1.4965 ×105=1.175 kW
(b) Breaking up the cylindrical surface, A2, into a bottom half, A4, and a top half, A5, leads to
0.52=6,F1−m=3−√9−1=0.1716,
F1−4=1−F1−m=0.8284,
F1−5=F1−m−F1−3=0.1716 −0.0557 =0.1158.
102 RADIATIVE HEAT TRANSFER
=3.3143 ×1012K4or T4=1349 K,
T5=15004[0.0290×(1−0.5858)+0.2071×0.1781]
q1=5.670×10−8h15004−13494×0.8284−11604×0.1158−5004×0.0557i
=1.1927 ×105W
CHAPTER 5 103
5.3 Repeat Problem 5.2 for a 20 cm high furnace of quadratic
(10 cm ×10 cm) cross-section.
q1=5.670 ×10−8h15004−12654×0.9314−5004×0.0686i=1.5147 ×105W
m2
and
Q1=a2q1=0.12×1.5147 ×105=1.5147 kW
(b) Breaking up the vertical surface, A2, into a bottom half, A4, and a top half, A5, leads to
q1=Eb1−Eb4F1−4−Eb5F1−5−Eb3F1−3,
is an artificial square at mid-height of the furnace, separating A4and A5. From Configuration 38,
X=Y=1,F1−m=2
π(ln 2
√3
+2√2 tan−11
√2−2 tan−11)=0.1998,
F1−4=1−F1−m=0.8002,
F1−5=F1−m−F1−3=0.1998 −0.0686 =0.1312.
=2.3180 ×1012K4or T4=1234 K,
T5=15004[0.0328×(1−0.5999)+0.2000×0.1672]
q1=5.670×10−8h15004−12344×0.8002−10644×0.1312−5004×0.0686i
Q1=0.12×1.7209 ×105=1.721 kW
CHAPTER 5 105
5.4 A small star has a radius of 100,000 km. Suppose that the star is originally at a uniform temperature of
1,000,000 K before it “dies,” i.e., before nuclear fusion stops supplying heat. If it is assumed that the star has a
constant heat capacity of ρcp=1 kJ/m3K, and that it remains isothermal during cool-down, estimate the time
required until the star has cooled to 10,000 K. Note: A body of such proportions radiates like a blackbody
(Why?).
t=1.960 ×105s=54.43 h
The extremely short cool-down time indicates the enormous amount of energy radiated from a blackbody
at 1,000,000 K. Of course, in reality, the star would not remain isothermal and the cooling time would be
106 RADIATIVE HEAT TRANSFER
5.5
A1
w=20cm
q0=10W/cm2
A collimated light beam of q0=10 W/cm2originating from a
blackbody source at 1250 K, is aimed at a small target A1=
Light reflected from A1travels on to a detector A2=1 cm2,
coated with the same material as A1.
How much of the collimated energy q0is absorbed by detector A2?
CHAPTER 5 107
5.6 Repeat Problem 5.2 for the case that the top surface of the furnace is coated with a gray, diffuse material with
emittance ǫ3=0.5 (other surfaces remain black).
0.5−11−1
2×0.9443=9.795 ×104W
Q1=π×0.052×9.795 ×104=770 W
Heat flux is reduced by 35% due to the reflection term in the denominator for q1.
The temperature of the side wall is found from
108 RADIATIVE HEAT TRANSFER
5.7 A long half cylindrical rod is enclosed by
a long diffuse, gray isothermal cylinder as
shown. Both rod and cylinder may be con-
sidered isothermal (T1=T2, ǫ1=ǫ2,T3, ǫ3) and
gray, diffuse reflectors. Give an expression for
the heat lost from the rod (per unit length).
j
j 1
RiRo
A2
A1
A3
CHAPTER 5 109
5.8
Consider a 90◦pipe elbow as shown in the figure (pipe diameter =
D=1 m; inner elbow radius =0, outer elbow radius =D). The elbow
is isothermal at temperature T=1000 K, has a gray diffuse emittance
ǫ=0.4, and is placed in a cool environment. What is the total heat loss
from the isothermal elbow (inside and outside)?
110 RADIATIVE HEAT TRANSFER
5.9
5 cm
2 cm
4 cm
A2
A3
A1
For the configuration shown in the figure, determine the temperature of Surface 2
with the following data:
Surface 1 : T1=1000 K,
q1=−1 W/cm2,
ǫ1=0.6;
Surface 2 : ǫ2=0.2;
Surface 3 : ǫ3=0.3,perfectly insulated.
All configurations are gray and diffuse.
Solution
ǫ1−1F2−1q1+1
ǫ2
and, from conservation of energy,
A1q1+A2q2=0.(5.9-C)
F2−3+F2−1F1−3=F2−3+F1−3(1−F2−3)=F1−3+F2−3(1−F1−3)
=F1−3+F1−2F2−3=F.
Therefore,
1
ǫ1−F2−1F1−3
Fq1−1
ǫ2−F1−2F2−3
Fq2=Eb1−Eb2.
R1=4
5,R2=3
5,X=1+1+4
25
16
25
=45
16,
F1−2=1
45
−1
=0.0919.
A2
=4.7179 ×1012 K4
T2=1474 K
112 RADIATIVE HEAT TRANSFER
5.10
A1
r
2r
2r
2r
A2
A3
Two pipes carrying hot combustion gases are enclosed in a cylindrical
duct as shown. Assuming both pipes to be isothermal at 2000 K and
diffusely emitting and reflecting (ǫ=0.5), and the duct wall to be
isothermal at 500 K and diffusely emitting and reflecting (ǫ=0.2),
determine the radiative heat loss from the pipes.
CHAPTER 5 113
5.11 A cubical enclosure has gray, diffuse walls which interchange energy. Four of the walls are isothermal at Ts
with emittance ǫs, the other two are isothermal at Ttwith emittance ǫt. Calculate the heat flux rates per unit
time and area.
114 RADIATIVE HEAT TRANSFER
5.12
a
aa
a
A1
T,
ϕ
ϕ
Panel
Door
∋
A2A3
During launch the heat rejector radiative panels of the Space Shuttle are
folded against the inside of the Shuttle doors. During orbit the doors
are opened and the panels are rotated out by an angle ϕas shown in the
figure. Assuming door and panel can be approximated by infinitely long,
isothermal quarter-cylinders of radius aand emittance ǫ=0.8, calculate
the necessary rotation angle ϕso that half the total energy emitted by panel
(2) and door (1) escapes through the opening. At what opening angle will
a maximum amount of energy be rejected? How much and why?
A12ǫ12Eb12 max
ǫ12 +(1 −ǫ12)2 √2/π
CHAPTER 5 115
5.13
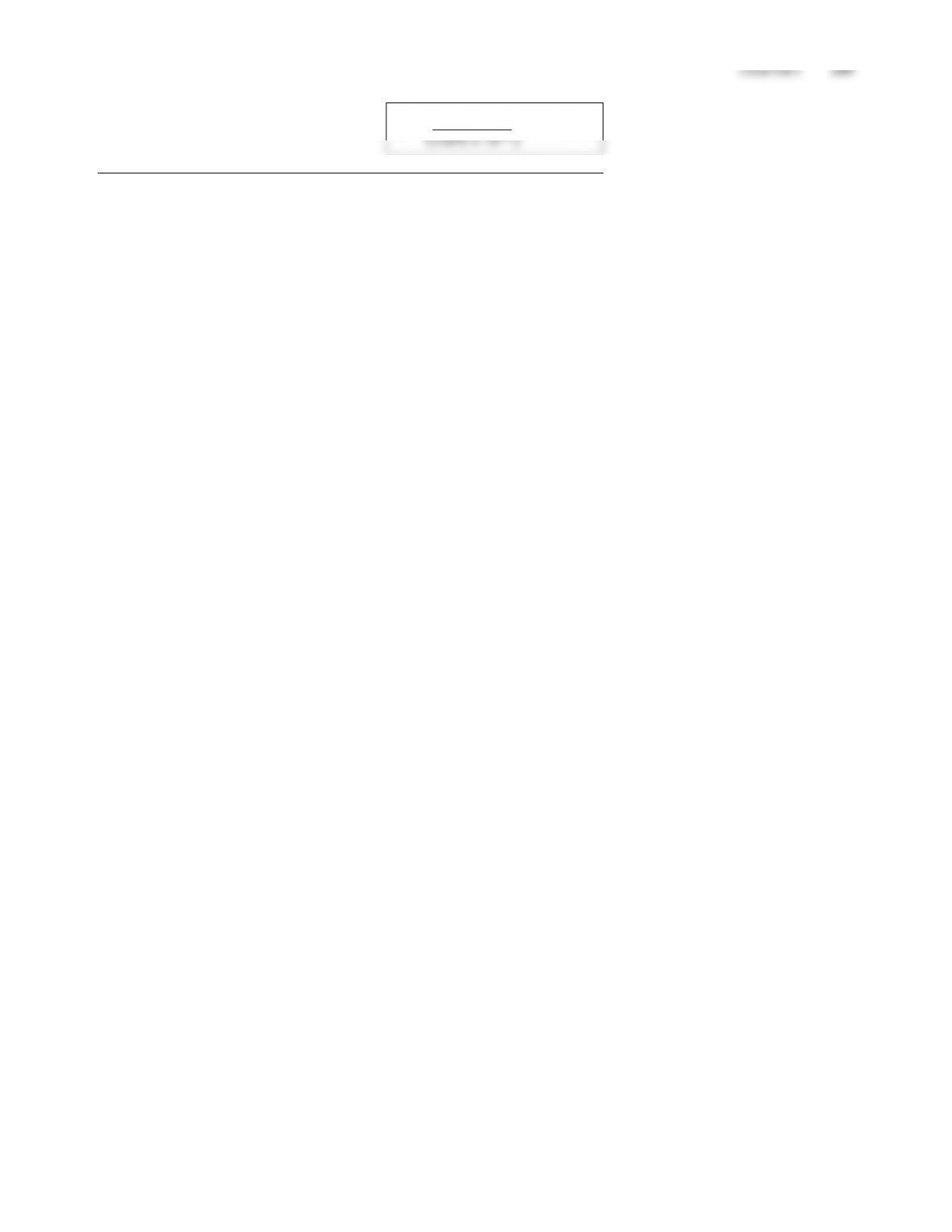
1m
1m
1m
A2
A1
(flat or grooved)
(1mm thick, insulated)
1cm
1cm A1 for case 2
(100 grooves)
Consider two 1 ×1 m2, thin, gray-diffuse plates located a distance h=1 m
apart. The temperature of the top plate is maintained at T1=1200 K, whereas
the bottom plate is initially at T2=300 K and insulated on the outside. In
case 1, the surface of the top plate is flat, whereas in case 2 grooves, whose
dimensions are indicated below, have been machined in the plate’s surface.
In either case the surfaces are gray and diffuse, and the surroundings may be
considered as black and having a temperature T∞=500 K; convective heat
transfer effects may be neglected.
(a) Estimate the effect of the surface preparation of the top surface on the
initial temperature change of the bottom plate (dT2/dt at t=0).
(b) Justify, then use, a lumped-capacity analysis for the bottom plate to predict the history of temperature
and heating rates of the bottom plate until steady-state is reached.
The following properties are known: Top plate: ǫ1=0.6,T1=1200 K; bottom plate: T2(t=0) =300 K,
ǫ2=0.5, ρ2=800 kg/m3(density),cp2=440 J/kg K,k2=200 W/m K.
Case 1 (A1is flat):
0.6=5
3,B=5
3−11
5=2
15
15 −1
5×5
31200
500 4−4
5×2
15 +4
5×5
3
2×5
3−(2 −1)1
5×2
15
D=
10
=0.4960
Case 2 (A1is grooved): calling a flat surface covering the grooved surface A1f, and noting that all radiation
from A2to A1passes through A1f, and all radiation from A2passing through A1ftravels on to A1, we have
2. Also, F2−∞ =4
5as before, and F1−∞ =1−F1−1−F1−2=
1−1
2=−1
10 =2
5. Thus
2×4
3−(2 −1) 1
10 ×2
15
D=
8
3−1
75
=0.4975,
q2=(−2.923 +0.4975 ×0.64)×5.670 ×10−85004=−10,130 W/m2.
q2
or dθ
dt =−q2
ρ2cp2δ2T∞
=C∗−D∗θ4,
where
θ=T2
;C∗=−c
;D∗=D
.
Case 1:
Case 2:
118 RADIATIVE HEAT TRANSFER
5.14
d
Inner wall
q = 300 kW/m2
3 = 0.3, q3 = 0
Outer wall,
s2 = 0.6
Silicon carbide rods (s/d = 2)
∋
∋
1 = 0.8
∋
A row of equally-spaced, cylindrical heating elements (s=2d) is used to
heat the inside of a furnace as shown. Assuming that the outer wall is
made of firebrick with ǫ3=0.3 and is perfectly insulated, that the heating
rods are made of silicon carbide (ǫ1=0.8), and that the inner wall has
an emittance of ǫ2=0.6, what must be the operating temperature of the
rods to supply a net heat flux of 300 kW/m2to the furnace, if the inner
wall is at a temperature of 1300 K?
=3.8248 ×105W/m2=(1−0.1628)Eb1−0.4186 Eb3
or, dividing by F1−3,
0.8−1×0.6576 ×191,000 −300,000
0.6−5.670 ×10−8×13004
=−6.9334 ×105W/m2=−0.6576 Eb1−0.3424 Eb3,
T1= 7.4933 ×105
=1907 K