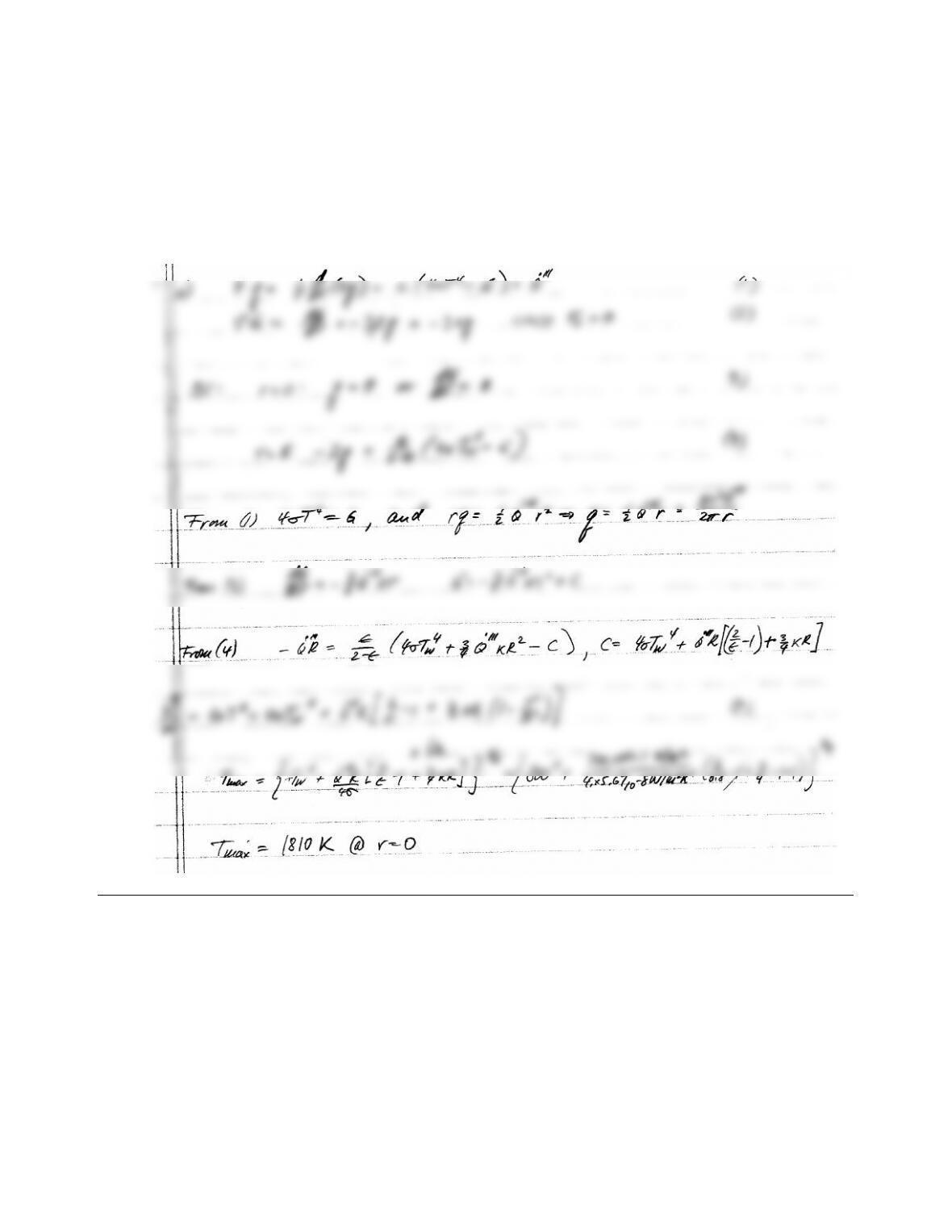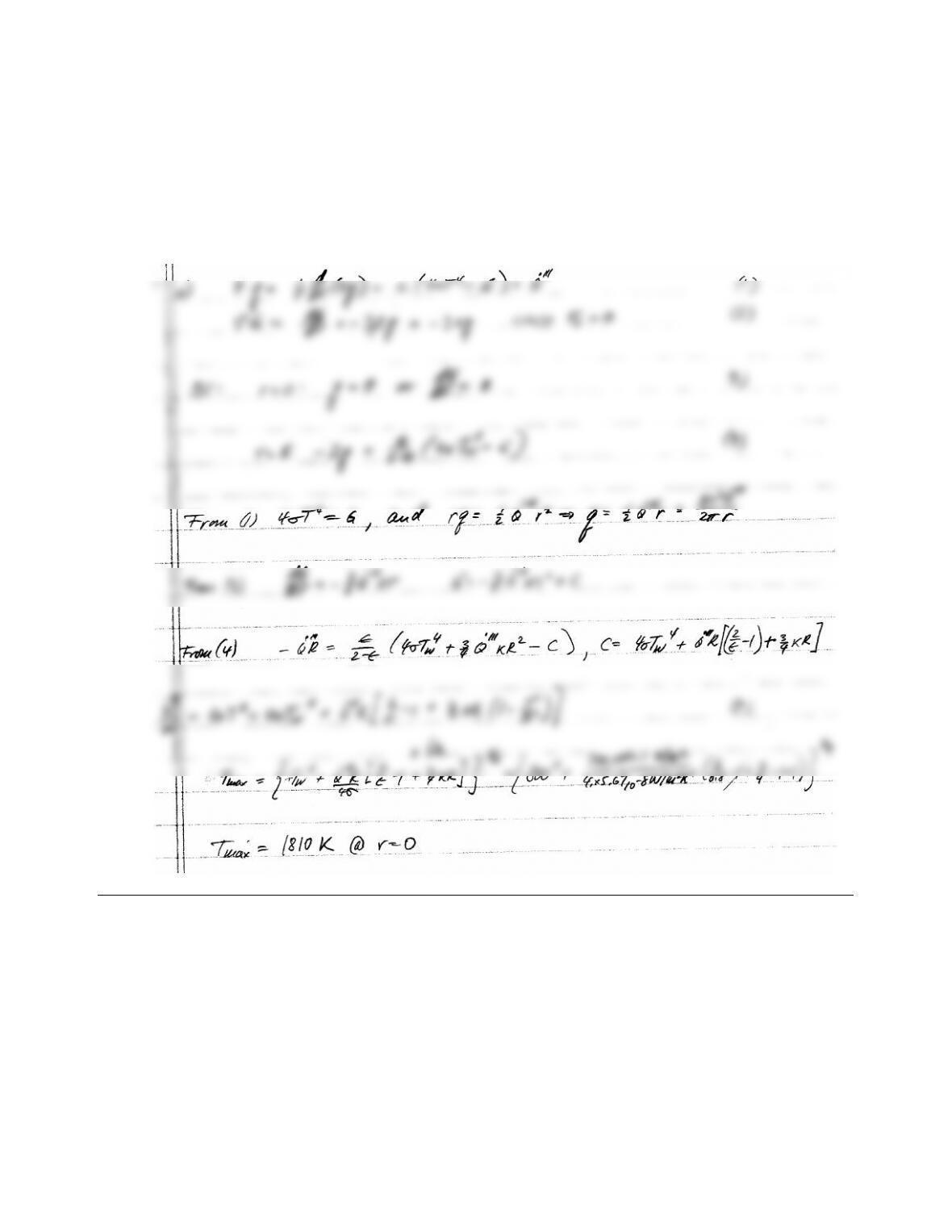CHAPTER 16 417
16.9 Two infinitely long concentric cylinders of radii R1and R2with emittances ǫ1and ǫ2both have the same
constant surface temperature Tw. The medium between the cylinders has a constant absorption coefficient κ
and does not scatter; uniform heat generation ˙
Q′′′ takes place inside the medium. Determine the temperature
distribution in the medium and heat fluxes at the wall if radiation is the only means of heat transfer by using
the P1-approximation.
Solution
From equation (16.35), (16.37) and (16.47) we have, also applying the condition of radiative equilibrium with
internal heat generation,
∇·q=1
d
Q′′′
Introducing b=4
31
ǫ−1
2,Φ = 4σ(T4−T4
w)
˙
Q′′′ /κ ,Ψ = q
˙
Q′′′ /κ, this becomes
1
τ
d
dτ(τΨ)=1,dΦ
dτ=−3Ψ,
τ=τ1:b1Φ′= Φ −1, τ =τ2:−b2Φ′= Φ −1.
Integrating:
Applying the boundary conditions,
2τ2+3C1
τ2=−3
4τ2
2−3C1ln τ2+C2−1.
Subtracting these two leads to
3
2(τ1b1+τ2b2)+3
4(τ2
2−τ2
1)
τ1
τ2
τ1
and
C2=1+ b2
τ2
+ln τ2!3C1+3
2τ2b2+3
4τ2
2.
4(τ2
τ2
τ2!+3
2τ2b2+1.
2−1
4τ
b1
τ1
+b2
τ2
+ln τ2
τ1
CHAPTER 16 419
16.10 An infinite, black, isothermal plate bounds a semi-infinite space filled with black spheres. At any given
distance, z, away from the plate the particle number density is identical, namely NT=6.3662 ×108m−3.
However, the radius of the suspended spheres diminishes monotonically away from the surface as
a=aoe−z/L;ao=10−4m,L=1 m.
(a) Determine the absorption coefficient as a function of z(you may make the large-particle assumption).
(b) Determine the optical coordinate as a function of z. What is the total optical thickness of the semi-infinite
space?
(c) Assuming that radiative equilibrium prevails and that the differential approximation is valid, set up the
boundary conditions.
(d) Solve for heat flux and temperature distribution (as a function of z).
T4
w
4+3τ∞
4+3τ∞
420 RADIATIVE HEAT TRANSFER
16.11 Consider two parallel black plates both at 1000 K, which are 2 m apart. The medium between the plates emits
and absorbs (but does not scatter) with an absorption coefficient of κ=0.05236 cm−1(gray medium). Heat is
generated by the medium according to the formula
˙
Q′′′ =CσT4,C=6.958 ×10−4cm−1,
where Tis the local temperature of the medium between the plates. Assuming that radiation is the only
important mode of heat transfer, determine the heat flux to the plates.
and (16.47), and applying the condition of radiative equilibrium with internal heat generation,
dq
dz =κ(4σT4−G)=˙
Q′′′ =CσT4,
dG
dz =−3κq,
subject to
τ=0 : 2q=4σT4
w−4−C
κσT4=4σT4
w−4κ
C−1dq
dτ(0),
and a similar boundary condition at τ=τL; however, the second boundary condition may be replaced by
C1=4σT4
0.1(4κ/C−1) cos 0.05τL−2 sin 0.05τL
=4×5.670 ×10−8×10004W/m2
=9078.8W
m2
CHAPTER 16 421
16.12 A furnace burning pulverized coal may be approximated by a gray cylinder at radiative equilibrium with
uniform heat generation ˙
Q′′′ =0.266 W/cm3, bounded by a cold black wall. The gray and constant absorption
and scattering coefficients are, respectively, 0.16 cm−1and 0.04 cm−1, while the furnace radius is R=0.5 m.
Scattering may be assumed to be isotropic. Using the P1-approximation:
(a) Set up the relevant equations and their boundary conditions;
(b) Calculate the total heat loss from the furnace (per unit length);
(c) Calculate the radial temperature distribution; what are centerline and adjacent-to-wall temperatures,
respectively?
(d) Qualitatively, keeping the extinction coefficient constant, what is the effect of varying the scattering
coefficient on (i) heat transfer rates, (ii) temperature levels?
=1.6625 (69
9),
since τR=(0.16 +0.04) cm−1×50 cm =10. Thus,
CHAPTER 16 423
16.13 The coal particles of Problem 12.3 are burnt in a long cylindrical combustion chamber of R=1 m radius. The
combustor walls are gray and diffuse, with ǫw=0.8, and are at 800 K. Since it is well stirred, combustion
results in uniform heat generation throughout of ˙
Q′′′ =720 kW/m3. Determine the maximum temperature in
the combustor, using the P1/differential approximation, assuming radiation is the only mode of heat transfer
(use κ=4.5 m−1and σs=0.5 m−1if results of Problem 12.3 are not available).
Solution
424 RADIATIVE HEAT TRANSFER
16.14 Estimate the radial temperature distribution in the sun. You may make the following assumptions:
(i) The sun is a sphere of radius R;
(ii) As a result of high temperatures in the sun the absorption and scattering coefficients may be approxi-
mated to be constant, i.e., κν, βν=const ,f(ν, T,r) (free-free transitions!);
(iii) Due to high temperatures, radiation is the only mode of heat transfer;
(iv) The fusion process may be approximated by assuming that a small sphere at the center of the sun releases
heat uniformly corresponding to the total heat loss of the sun (i.e., assume the sun to be concentric spheres
with a certain heat flux at the inner boundary r=ri).
(a) Relate the heat production to the effective sun temperature TSHMeff=5777 K.
(b) Would you expect the sun to be optically thin, intermediate, or thick? Why? What are the prevailing
boundary conditions?
(c) Find an expression for the temperature distribution (for r>ri).
(d) What is the surface temperature of the sun?
Solution
(a) The total heat leaving the sun, assuming steady state, must equal the internal heat production. Since the
(b) The sun is optically very thick: Shooting a light beam of any wavelength into the sun we would hardly
expect to find a fraction exiting from the other side! Thus, the P1-approximation should do well to model the
sun. Boundary conditions: At r=rithe total amount of heat generation goes into the outer sun over an area
of 4πr2
i, or
τ=τR:−2q=−G.
where we have also scattering assumed to be isotropic. Thus, 4σT4=Gand
τ2q=const =τ2
RqR.
426 RADIATIVE HEAT TRANSFER
16.15 Repeat Problem 16.14 but replace assumption (iv) by the following: The fusion process may be approximated
by assuming that the sun releases heat uniformly throughout its volume corresponding to the total heat loss
of the sun.
428 RADIATIVE HEAT TRANSFER
16.18 A revolutionary new fuel is ground up into small particles, magnetically confined to remain within a spherical
cloud of radius R. This cloud of particles has a constant, gray absorption coefficient, does not scatter, and
releases heat uniformly at ˙
Q′′′ (W/m3). The cloud is suspended in a vacuum chamber, enclosed by a large,
isothermal chamber (at Tw). Heat transfer is solely by radiation, i.e., ∇·q=1/r2dr2q/dr =˙
Q′′′ .
(a) Assuming the P-1 approximation to be valid, set up the necessary equations and boundary conditions to
determine the heat transfer rates, and temperature distribution within the spherical cloud.
(b) Determine the maximum temperature in the cloud.
κ1+2
3κR+1
2(κR)2+4σT4