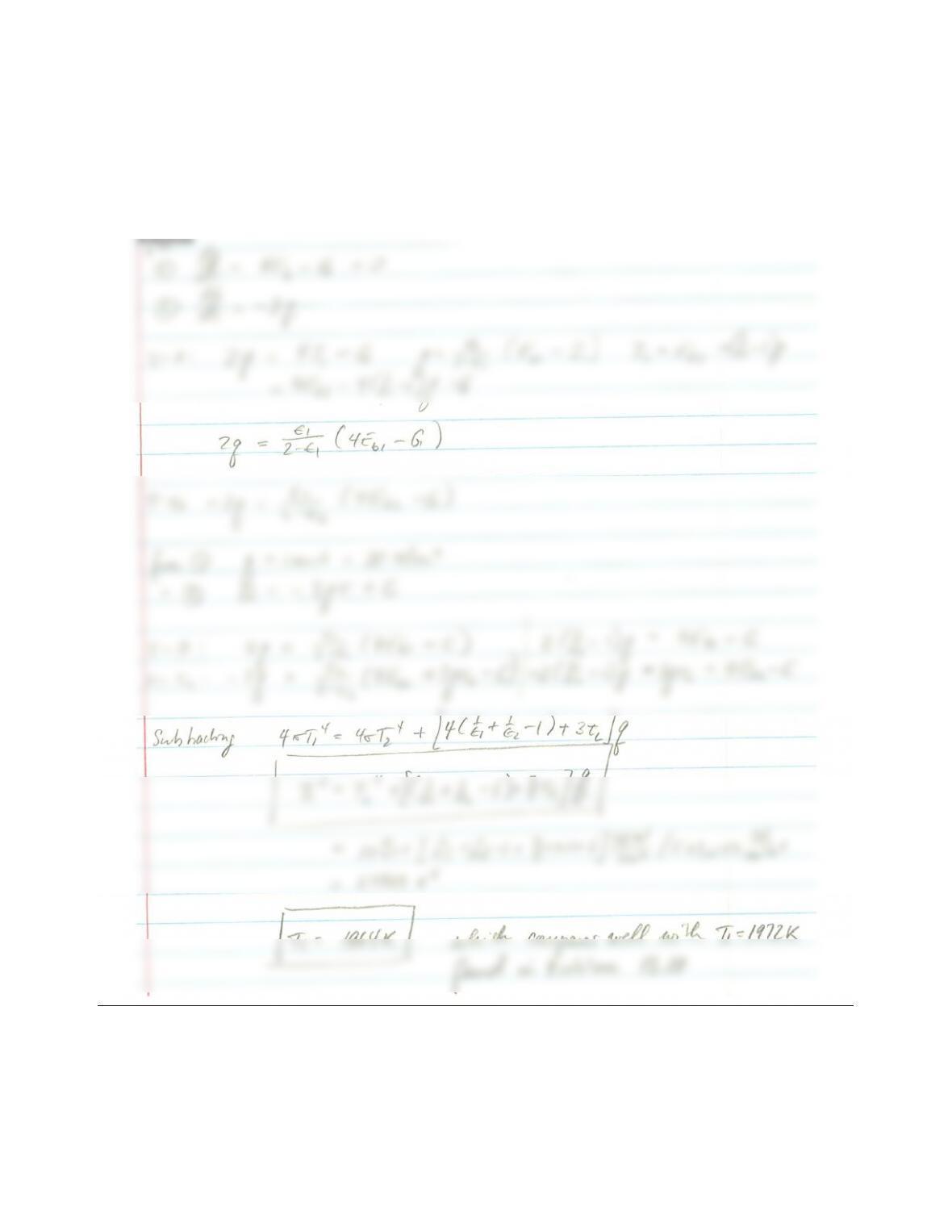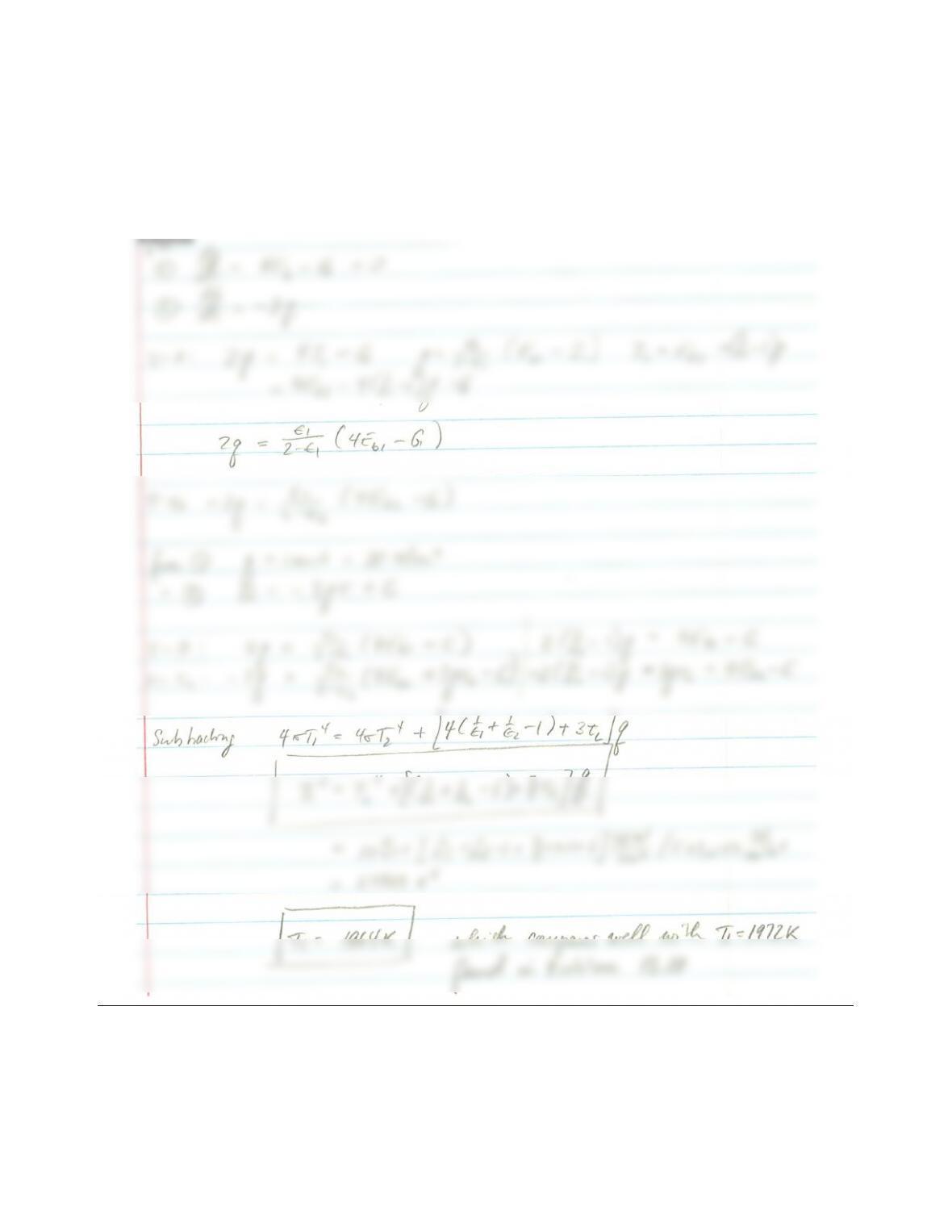CHAPTER 15 391
Tmax =2172 K,
Q′′′
392 RADIATIVE HEAT TRANSFER
15.12 Do Problem 15.10 using the Milne-Eddington approximation.
394 RADIATIVE HEAT TRANSFER
15.13 Do Problem 15.10, using the exponential-kernel approximation.
Note: The necessary exact integral relations have been given in Problem 14.3.
2 cosh 3
8τL+sinh 3
8τL
396 RADIATIVE HEAT TRANSFER
15.14 Consider (a) two parallel plates, (b) two concentric spheres. The bottom/inner surface needs to dissipate a
heat flux of 30 W/cm2and has a gray-diffuse emittance ǫ1=0.5. The top/outer surface is at T2=1000 K with
ǫ2=0.8. The medium in between the surfaces is gray and nonscattering (κ=0.1 cm−1), has a thickness of
L=5 cm and is at radiative equilibrium. Determine the temperature at the bottom/inner surface necessary to
dissipate the supplied heat for the two different cases (the radius of the inner sphere is R1=5 cm), using the
Milne-Eddington approximation. Compare with the results of Problem 14.12.
CHAPTER 15 397
15.15 A material produces an amount of heat that is constant per unit volume, i.e., ˙
Q′′′ =const. This heat
production needs to be removed by thermal radiation. It is proposed to grind up the (fixed volume of) material
into small particles, which are to be suspended evenly between two cold plates of (identical) emissivity ǫ.
Since it is important to keep the overall temperature level in the particles as low as possible, should the
particles be ground as fine as possible, as large as possible, or does some optimum radius exist? What is the
optimum particle size, and what is the maximum temperature if this size is employed? You may assume
one-dimensional parallel plates with a constant volume fraction of particles, black particles with relatively
large size parameters, and you may use the Schuster-Schwarzschild approximation.
CHAPTER 15 399
15.16 Do Problem 15.15 using the Milne-Eddington (differential) approximation.
=1
=fv
4˙
ǫ−1+r3
2
CHAPTER 15 401
15.18 Consider parallel, black plates, spaced 1 m apart, at constant temperatures T1and T2. Due to pressure
variations, the (gray) absorption coefficient is equal to
κ=κ0+κ1z;κ0=0.01 cm−1;κ1=0.0002 cm−2,
where zis measured from Plate 1. The medium does not scatter radiation. Determine, for radiative equi-
librium, the nondimensional heat flux Ψ = q/σ(T4
1−T4
2) by (a) the exact method, (b) the regular diffusion
approximation, (c) the diffusion approximation with jump boundary conditions, (d) the two-flux method, (e)
the differential approximation, and (f) the kernel approximation.
(a) Exact: From Table 14.1 Ψ = 0.3900.
(b) Regular diffusion: From equation (15.16)
σ(T4
1−T4
2)=4
3τL
(c) Diffusion with jump condition: Again,
2q=σT4
τ=τL:−1
2q=σT4
2−σT4(τL)=σT4
1−C+3
4qτL.
Subtracting gives
τ=0 : 2q=4σT4
1−G=4σT4
1−C,
τ=τL:−2q=4σT4
2−G=4σT4
1−C+4qτL,
CHAPTER 15 403
15.19 An infinite, black, isothermal plate at 1000 K bounds a semi-infinite space filled with black spheres of uniform
radius a=100 µm. The particle number density is maximum adjacent to the surface, and decays exponentially
away from the surface according to
NT=N0e−Cz;N0=108m−3,C=πm−1.
(a) Determine the absorption and extinction coefficients as functions of z.
(b) Determine the optical coordinate as a function of z. What is the total optical thickness of the semi-infinite
space?
(c) Assuming that radiative equilibrium prevails and using the Milne-Eddington approximation, set up the
boundary conditions and solve for heat flux and temperature distribution (as a function of z).
w
4τ∞
4×1=4
