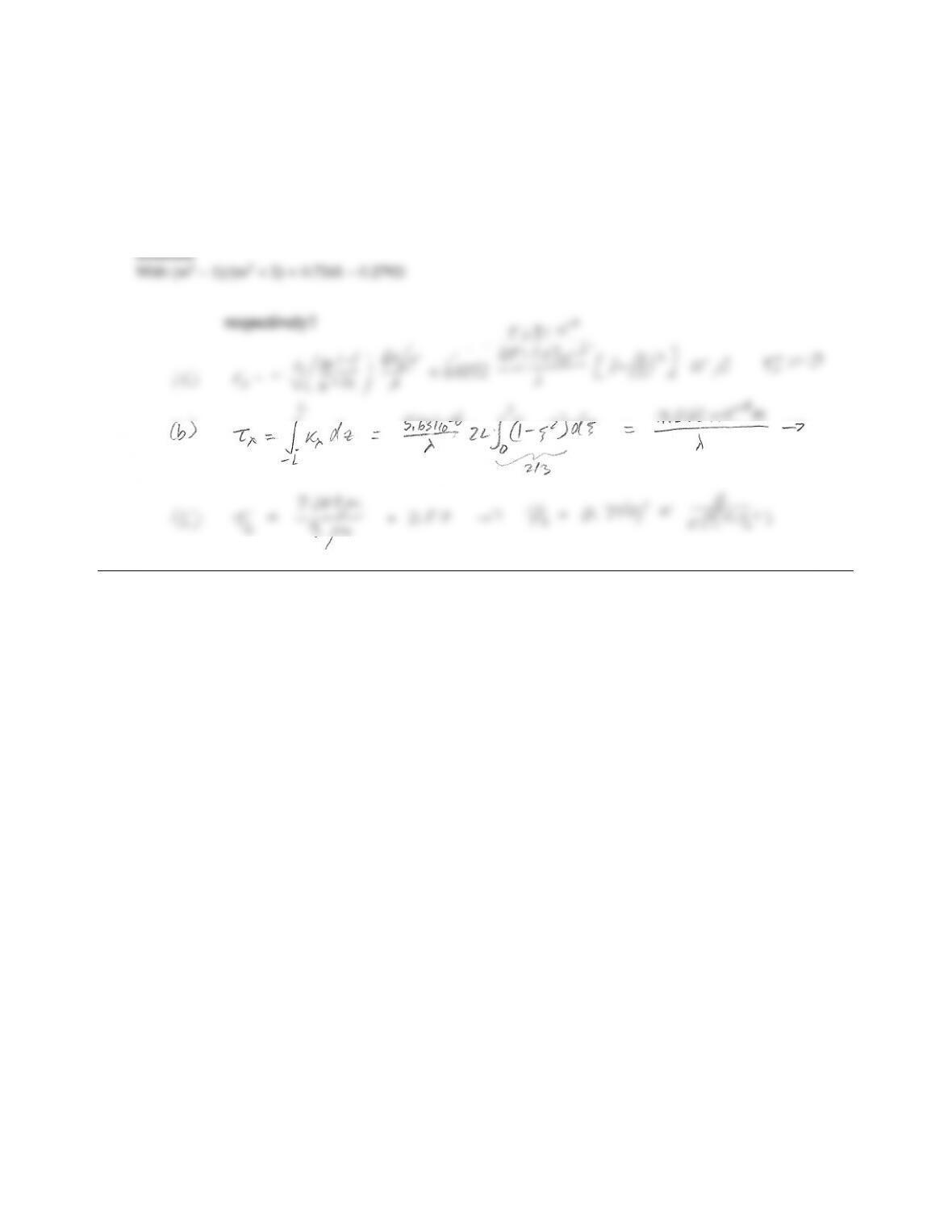350 RADIATIVE HEAT TRANSFER
12.13 A semi-infinite space is filled with black spheres. At any given distance, z, away from the plate the particle
number density is identical, namely NT=6.3662 ×108m−3. However, the radius of the suspended spheres
diminishes monotonically away from the surface as
a=a0e−z/L;a0=10−4m,L=1 m.
(a) Determine the absorption coefficient as a function of z(you may make the large-particle assumption).
(b) Determine the optical coordinate as a function of z. What is the total optical thickness of the semi-infinite
space?
CHAPTER 12 351
12.14 A semi-infinite space is filled with black spheres of uniform radius a=100 µm. The particle number density
is maximum adjacent to the surface, and decays exponentially away from the surface according to
NT=N0e−Cz;N0=108m−3,C=πm−1.
(a) Determine the absorption and extinction coefficients as functions of z.
(b) Determine the optical coordinate as a function of z. What is the total optical thickness of the semi-infinite
space?
352 RADIATIVE HEAT TRANSFER
12.15 In a combustion chamber radiatively nonparticipating gases are mixed with soot and coal particles. The
following is known (per m3of mixture):
Soot: uniform particle size, as=10 nm, mass =10−3kg,
complex index of refraction m2−1
m2+2=0.5λ2−0.1λi(λin µm).
Coal: uniform particle size, ac=1 mm, mass =1 kg, coal is black.
Density of both, coal and soot, is 2,000 kg/m3.
Determine the spectral absorption coefficient of the mixture for the near infrared.
3πa3
cρcπa2
=3
4
mc
ρcac
=3
4
1 kg/m3
2000 kg/m3×1mm =0.375m−1
Total absorption coefficient:
κλ=κλs+κλc=0.942 +0.375 =1.317m−1.
CHAPTER 12 353
12.16 In a sheet flame confined between two large parallel plates −L≤z≤+L=1 m soot is generated mainly in the
central flame region, leading to a local soot volume fraction of fv(z)=fv0[1 −(z/L)2], with fv0=1.07 ×10−6.
The soot is propane soot with a complex index of refraction of m=2.21 −1.23i.
(a) Determine the relevant radiative properties of the mixture, assuming the combustion gases to be non-
participating.
(b) What is the spectral optical thickness of the 2Lthick layer?
354 RADIATIVE HEAT TRANSFER
12.17 A laser beam at 633 nm wavelength is probing a 1 m thick layer of gold nanoparticles suspended in air (radius
a=10 nm; for gold at 633 nm: m=0.47 −2.83i). If the exiting laser beams is attenuated by 10% due to
absorption and scattering, determine
(a) the number density of gold particles,
(b) their volume fraction.
CHAPTER 12 355
12.18 A LIDAR laser beam (operating in the green at λ=0.6µm) is shot into the sky. At a height of 1km the
laser encounters a 200m thick cloud consisting of tiny water droplets of varying size (1 nm ≤a≤20 nm), but
constant particle distribution function everywhere (n=6×1015/nm m3).
1. Determine the water droplet volume fraction in the cloud.
2. Determine its spectral absorption coefficient; compare with equation (12.123).
3. What fraction of the laser beam will be transmitted through the cloud? How much will be absorbed?
Note: Water at 0.6µm has an index of refraction of m≃1.35 −10−7i.
Solution
356 RADIATIVE HEAT TRANSFER
12.19 Redo Problem 12.4 for propane soot with a single mean radius of am=0.1µm in a flame with f0=10−6and
T0=1500 K. Show that the small particle limit is appropriate for, say, λ > 3µm. For hand calculations you
may approximate the index of refraction by a single average value (say, at 3 µm), and the emissive power by
Wien’s law.
=1.03693
=266.3 m−1K−1.
CHAPTER 12 357
Thus,
βP=2.5212 ×10−6×266.3 m−1K−11500 K(1+ξ)2=1.007(1+ξ)2m−1.
λ=2.5212 m−1(1+ξ). λ
µm!;βP=3.83 fvC0T
C2
358 RADIATIVE HEAT TRANSFER
12.20 Redo Problem 12.19 for the case that the soot has agglomerated into mass fractal aggregates of 1000 soot
particles each (Df=1.77 and kf=8.1).
Ca
sca
NCp
sca
=193.71−1000−1/4=75.9
and
Thus, with 74.9×1.566 =117.3
βλ=2.521 m−1(1+ξ), λ
µm!+117.3m−1, λ
µm!4
.
To evaluate the Planck-mean extinction coefficient, we first evaluate the Planck-mean scattering coefficient
for single particles
Ebλd(λT)
=C1
σ
i=1Z∞
0
y7e−iC2ydy =C1
σC5
2
i=1
i8Z∞
0
x7e−xdx
| {z }
=Γ(8)=1344
=1344C1
∞
X
1
=1344×3.742×10−16W m21.00408
=4.847 ×109m−4K−4.
Thus,
σp
P=1.566 ×10−24m3(1+ξ)[1500 K(1+ξ)]44.847 ×109m−4K−4
CHAPTER 12 359
12.21 Consider a particle cloud with a distribution function of n(a)=Ca2e−ba, where ais particle radius and band
Care constants. The particles are soot (m≃1.5−0.5i), and measurements show the soot occupies a volume
fraction of 10−5, while the number density has been measured as NT=1012/cm3. Calculate the extinction,
absorption, and scattering coefficients of the cloud for the wavelength range 1 µm<λ<4µm.