5-141
5-148E A plane wall in space is subjected to specified temperature on one side and radiation and heat flux on the other. The
finite difference formulation of this problem is to be obtained, and the nodal temperatures under steady conditions are to be
determined.
Assumptions 1 Heat transfer through the wall is given to be steady and
one-dimensional. 2 Thermal conductivity is constant. 3 There is no heat
generation. 4 There is no convection in space.
Properties The properties of the wall are given to be k=1.2 Btu/hft°F,
= 0.80, and
s = 0.6.
Analysis The nodal spacing is given to be x = 0.1 ft. Then the number of
nodes becomes
1/ += xLM
= 0.3/0.1+1 = 4. The left surface
temperature is given to be T0 = 520 R = 60F. This problem involves 3
T0
x
1
qs
•
•
•
•
0
2
3
Tsurr
5-142
5-149 A nuclear fuel element, modeled as a plane wall, generates 3 107 W/m3 of heat uniformly with both side surfaces
cooled by liquid. The finite difference equations and the nodal temperatures are to be determined, and the surface
temperatures of both sides of the fuel element are to be compared with analytical solution.
Assumptions 1 Heat transfer through the nuclear fuel element is
steady and one-dimensional. 2 Thermal properties are constant. 3
Heat transfer by radiation is negligible.
Properties The thermal conductivity is given as 57 W/m∙K.
Analysis (a) The nodal spacing is given as Δx = 8 mm. Then the
number of nodes M becomes
mm 40
L
m = 5:
0)/()2/()()/1( 5
2
54 =+++−
TkxhkexTkxhT
(b) The nodal temperatures under steady conditions are determined by solving the 6 equations above simultaneously with an
equation solver. Copy the following lines and paste on a blank EES screen to solve the above equations:
e_gen=3E7
h=8000
k=57
2
3
4
5-143
(c) Using the analytical solution from Chapter 2, for a plane wall of thickness 2L with heat generation, the surface
temperature exposed to convection can be determined using
)m 02.0)( W/m103(
37
gen
Le
5-144
5-150 A fuel element, modeled as a plane wall, generates 5 107 W/m3 of heat uniformly with both side surfaces cooled by
liquid. The finite difference equations and the nodal temperatures are to be determined by making use of the symmetry line of
the plane wall.
Assumptions 1 Heat transfer through the fuel element is steady and one-dimensional. 2 Thermal properties are constant. 3
Heat transfer by radiation is negligible.
Properties The thermal conductivity is given as 67 W/m∙K.
Analysis (a) The nodal spacing is given to be Δx = 4 mm. Then the number
of nodes M becomes
mm 20
L
5-145
5-151 A square cross section with uniform heat generation is undergoing a steady two-dimensional heat transfer. The top and
right surfaces are subjected to convection while the left and bottom surfaces maintain a constant temperature. The finite
difference equations and the nodal temperatures are to be determined.
Assumptions 1 Steady heat conduction is two-dimensional. 2 Thermal properties are constant. 3 The heat generation in the
body is uniform.
Properties The conductivity is given to be k = 25 W/m∙K.
Analysis (a) There is symmetry about the diagonal line passing through the center. Therefore, T1 = T4, and the unknown
temperatures are T1, T2, and T3. Thus, we need to have 3 equations to determine them uniquely.
200
1
13
12
−
−
−
y
T
y
TT
TT
y
5-147
5-153 Starting with an energy balance on a disk volume element, the one-dimensional transient implicit finite difference
equation for a general interior node for
),( tzT
in a cylinder whose side surface is subjected to convection with a convection
coefficient of h and an ambient temperature of T for the case of constant thermal conductivity with uniform heat generation
is to be obtained.
Analysis We consider transient one-dimensional heat conduction in
the axial z direction in a cylindrical rod of constant cross-sectional
area A with constant heat generation
0
e
and constant conductivity k
Convection
h, T
Disk
5-152
Therefore, any time step less than 8.779 s can be used to solve this problem. For convenience, let us choose the time step to
be ∆t = 6 s. Then the mesh Fourier number becomes
32544.0
)m 025.0(
)s 6)(s/m 109.33(
2
26
2=
=
=
−
x
t
(for ∆t = 6 s)
(c) With the initial nodal temperatures of 650°C, the results obtained from successive iterations are listed in the following
table:
Time
step, i
Time,
s
Nodal temperature,°C
i
T0
i
T1
i
T2
i
T3
i
T4
0
0
650
650
650
650
650
1
6
629.3
650
650
650
650
2
12
622.8
643.3
650
650
650
3
18
616.3
638.8
647.8
650
650
4
24
611.4
634.4
645.6
649.3
650
5
30
607.0
630.6
643.2
648.3
649.5
6
36
603.1
627.0
640.7
647.0
648.7
7
42
599.5
623.7
638.3
645.5
647.6
8
48
596.2
620.6
635.9
643.9
646.3
9
54
593.2
617.6
633.5
642.1
644.7
10
60
590.3
614.8
631.1
640.1
643.0
(d) From Chapter 4, the approximate analytical solution is given as
),(
2
1LxeA
TtxT
−
=
−
5-154
To start the Solve Table at 2 go to ‘Calculate’ and select ‘Solve table’ (or hit F3) and make the ‘First Run
Number’ as 2. The initial temperatures and the initial time ‘0’ can be set manually in the parametric table“
Row = TableRun#
Time = TableValue(‘Table 1′, Row-1, #Time)+DELTAt/60
Duplicate i = 0,7
T_old[i] = TableValue(‘Table 1′, Row-1, #T[i])
End
” Finite difference equations”
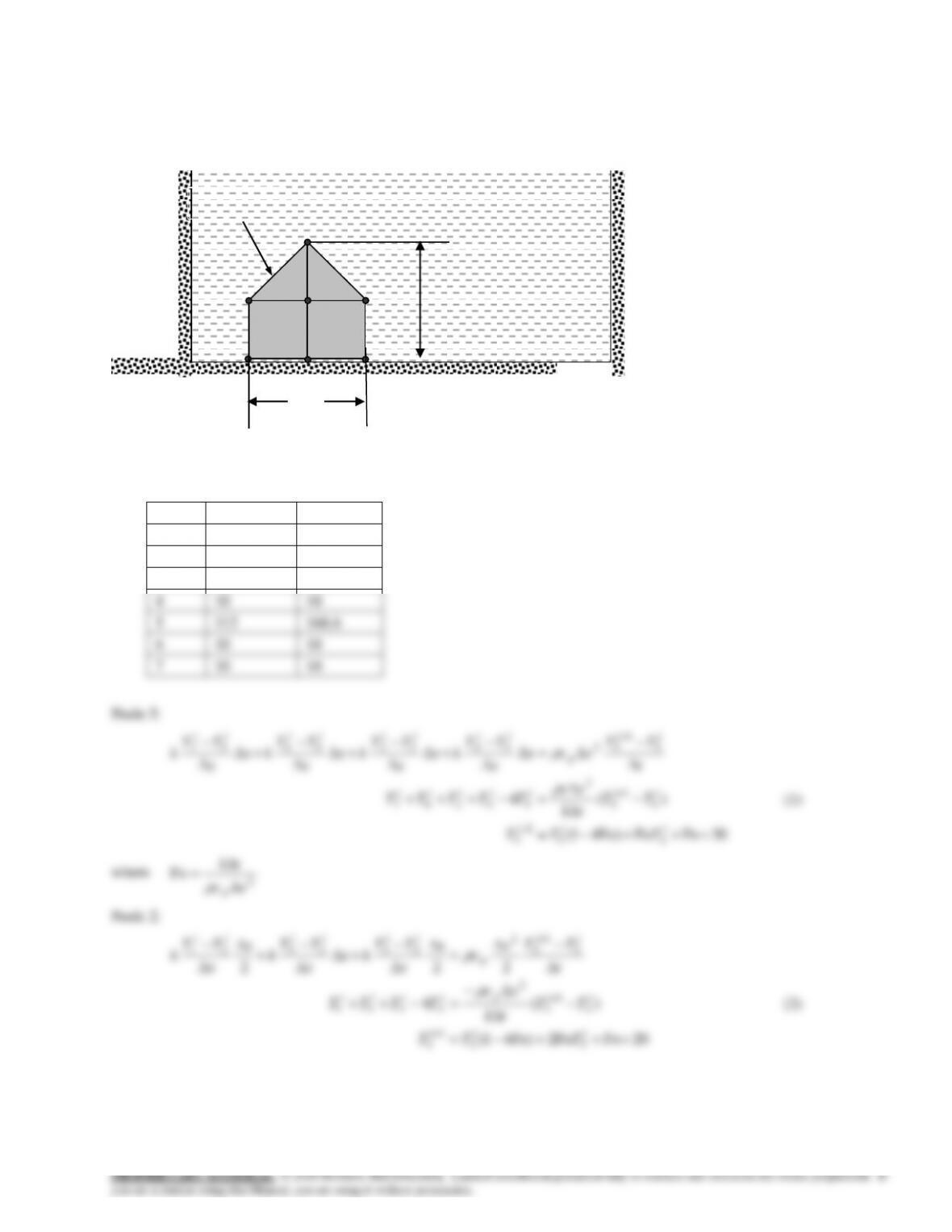
“Node 0” 2*T[1]-2*T[0]+e_gen*DELTAx^2/k_1 = (T[0] – T_old[0])/tau_1
“Node 1” T[0]-2*T[1]+T[2]+e_gen*DELTAx^2/k_1 = (T[1] – T_old[1])/tau_1
“Node 2” T[1]-2*T[2]+T[3]+e_gen*DELTAx^2/k_1 = (T[2] – T_old[2])/tau_1
“Node 3” T[2]-2*T[3]+T[4]+e_gen*DELTAx^2/k_1 = (T[3] – T_old[3])/tau_1
“Node 4” T[3]-2*T[4]+T[5]+e_gen*DELTAx^2/k_1 = (T[4] – T_old[4])/tau_1
“Node 5” k_1*(T[4]-T[5])/DELTAx + k_2*(T[6]-T[5])/DELTAx+e_gen*(DELTAx/2) =
1/2*(((rho_1*c_1*DELTAx)/DELTAt)+(((rho_2*c_2*DELTAx)/DELTAt)))*(T[5]-T_old[5])
“Node 6” T[5]-2*T[6]+T[7] = (T[6] – T_old[6])/tau_2
“Node 7” 2*(T[6]-T[7])+2*DELTAx*h/k_2*(T_infi-T[7]) = (T[7]-T_old[7])/tau_2
Temperature distribution in the fuel rod and cladding at different times
Node temperature (oC)
Time = 10 min
Time = 20 min
Time = 30 min
Node temperature (oC)
T0
468.3
389.8
339.1
T1
464.1
386.1
335.9
T2
451.4
375.2
326.5
T3
430.3
357.1
310.9
T4
400.8
331.9
289.1
T5
362.9
299.8
261.3
T6
257.2
213
187
T7
140
120.4
109
Discussion In most of the practical cases, during the cooling of nuclear reactor rods, the water used for convective cooling
undergoes a phase change process that enhances the rate of heat removal from the nuclear rods. Determination of the exact
heat transfer rates to the cooling water and the estimation of pressure drop due to two– phase flow of water (as the water
undergoes phase change) are quite challenging.
5-155
5-159 Starting with an energy balance on a volume element, the two-dimensional transient explicit finite difference equation
for a general interior node in rectangular coordinates for T(x, y, t) for the case of constant thermal conductivity k and uniform
heat generation
0
e
is to be obtained.
Analysis (See Figure 5-24 in the text). We consider a rectangular region in which heat conduction is significant in the x and y
directions, and consider a unit depth of z = 1 in the z direction. There is uniform heat generation in the medium, and the
thermal conductivity k of the medium is constant. Now we divide the x-y plane of the region into a rectangular mesh of nodal
5-156
5-160 A two-dimensional long steel bar shown in the figure is considered. The finite difference equations for the unknown
temperatures in the grid using the explicit method is to be written and dimensionless parameters are to be identified. Also, the
range of time steps for stability condition and the temperature field at certain times are to be determined.
Assumptions 1 Heat transfer through the body is transient and two-dimensional. 2 All surafces of the bar except the bottom
surface are maintained at a constant temperature. 3 Thermal conductivity is constant. 4 There is no heat generation.
Analysis (a) the finite difference equations for the unknown temperatures in the grid using the explicit method are
Node
T (10 s)
T (20 s)
1
10
10
2
443.3
234.4
3
10
10
4
10
10
5
315
168.6
6
10
10
7
10
10
20FoFo2)Fo41(
52
1
2
++−=
+
iii
TTT
tk
Ts = 10C
1
8
6
5
4
7
3
5 cm
2
5
5 cm
5-157
(b) For both steps, stability condition is
⎯→⎯⎯→⎯−
4
1
4
1
Fo0Fo41
2
xc
tk
p
5-158
Fundamentals of Engineering (FE) Exam Problems
5-161 The unsteady forward-difference heat conduction for a constant area, A, pin fin with perimeter, p, exposed to air whose
temperature is T0 with a convection heat transfer coefficient of h is
*
2
0
2
*
1
*
1
2
1* 2
1m
p
p
mm
p
mT
Ac
hp
xc
k
T
A
xhp
TT
xc
k
T
−
−−
++
=+−
+
In order for this equation to produce a stable solution, the quantity
Ac
hp
xc
k
p
p
+
2
2
must be
(a) Negative (b) zero (c) Positive (d) Greater than 1 (e) Less than 1
5-162 Air at T0 acts on top surface of the rectangular solid shown in
Fig. P5-162 with a convection heat transfer coefficient of h. The
correct steady-state finite-difference heat conduction equation for
node 3 of this solid is
(a) T3 = [(k/2)( T2 + T4 + T7) + hT0] / [(k/) + h]
(b) T3 = [(k/2)( T2 + T4 + 2T7) + hT0] / [(2k/) + h]
(c) T3 = [(k/)( T2 + T4 ) + hT0] / [(2k/) + h]
(d) T3 = [(k/)( T2 + T4 + T7) + hT0] / [(k/) + h]
(e) T3 = [(k/)( 2T2 + 2T4 + T7 ) + hT0] / [(k/) + h]
5-163 What is the correct unsteady forward-difference heat conduction equation of node 6 of the rectangular solid shown in
Fig. P5-163 if its temperature at the previous time (
t) is
*
6
T
?
*
6
2*
10
*
7
*
2
*
5
21
6
*
6
2*
10
*
7
*
2
*
5
21
6
*
6
2*
10
*
7
*
2
*
5
21
6
*
6
2*
10
*
7
*
2
*
5
21
6
*
6
2*
10
*
7
*
2
*
5
21
6
)/(41)()/(2 )(
)/(21)()/(2 )(
)/(2)()/( )(
)/(1)()/( )(
)/(41)()/( )(
TctkTTTTctkTe
TctkTTTTctkTd
TctkTTTTctkTc
TctkTTTTctkTb
TctkTTTTctkTa
pp
i
pp
i
pp
i
pp
i
pp
i
−++++=
−++++=
++++=
−++++=
−++++=
+
+
+
+
+
T0, h
• • • •
1
5
9
2 3
10
6
7
11
• • • •
• • • •
4
8
12
x =
y =
• • • •
1
5
9
2 3
10
6
7
11
• • • •
• • • •
4
8
12
x =
y =
