5-25 A pin fin with negligible heat transfer from its tip is considered. The complete finite difference formulation for the
determination of nodal temperatures is to be obtained.
Assumptions 1 Heat transfer through the pin fin is given to be steady and one-dimensional, and the thermal conductivity to
be constant. 2 Convection heat transfer coefficient is constant and uniform. 3 Radiation heat transfer is negligible. 4 Heat
loss from the fin tip is given to be negligible.
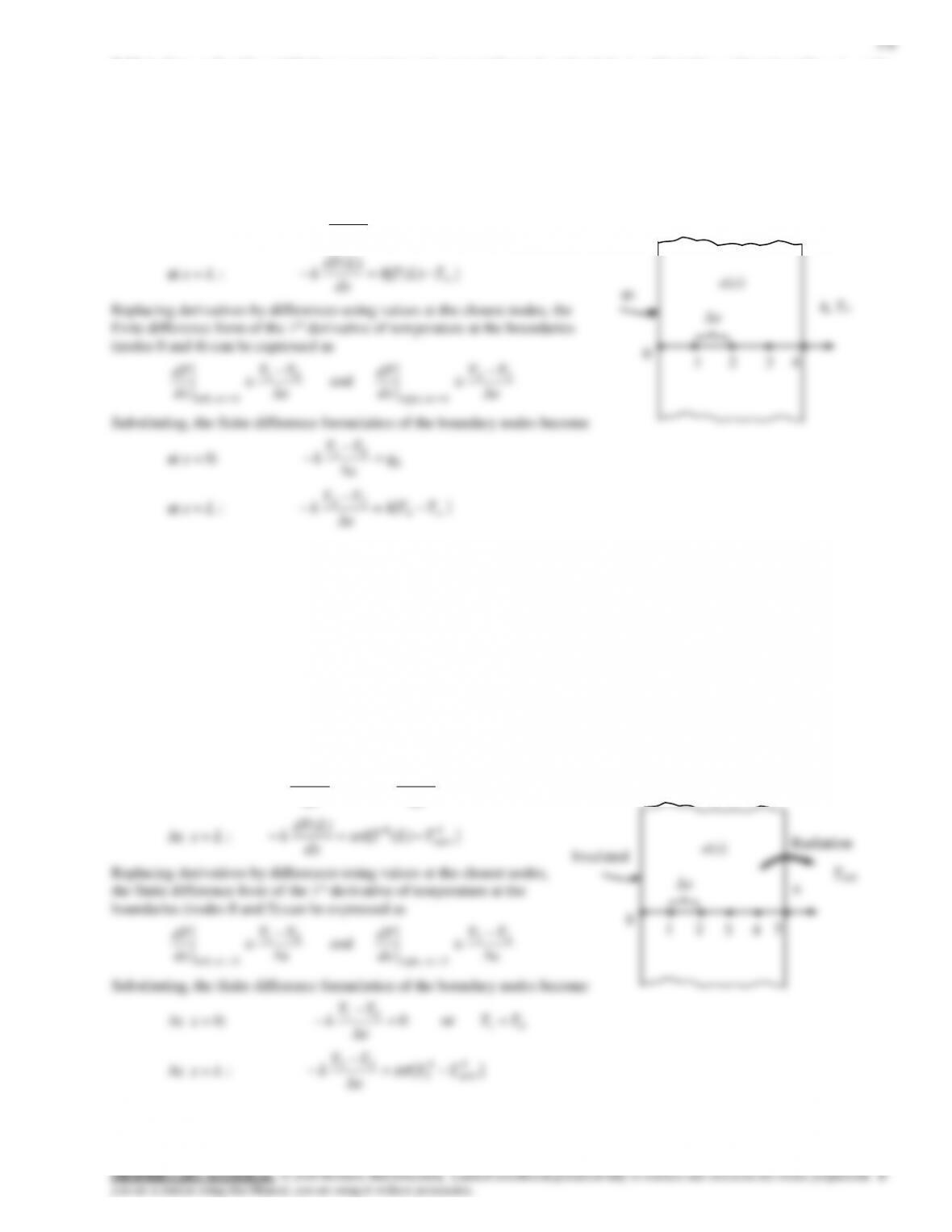
Analysis The nodal network consists of 3 nodes, and the base temperature T0 at
node 0 is specified. Therefore, there are two unknowns T1 and T2, and we need
two equations to determine them. Using the energy balance approach and taking
the direction of all heat transfers to be towards the node under consideration, the
finite difference formulations become
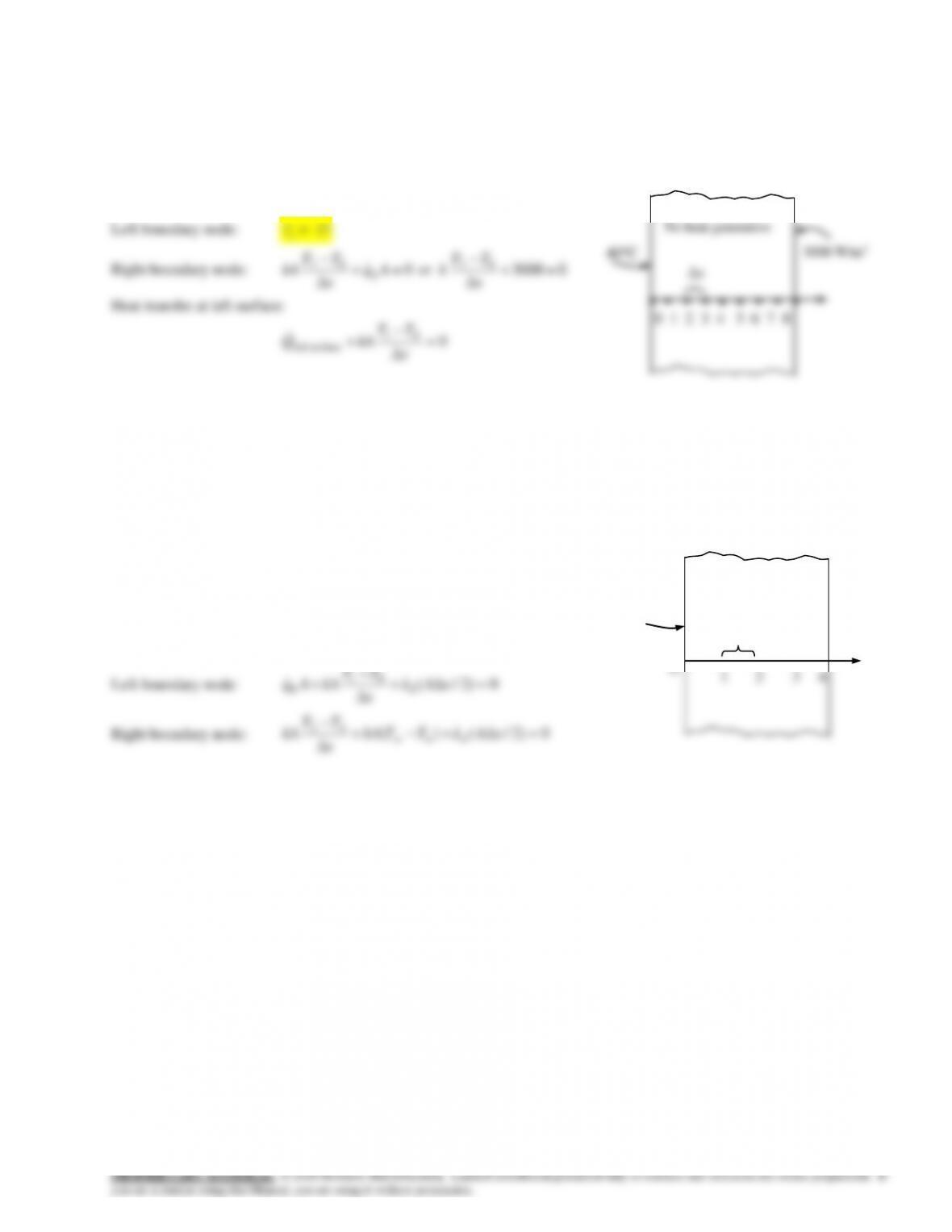
5-26 A plane wall with variable heat generation and constant thermal conductivity is subjected to combined convection,
radiation, and heat flux at the left (node 0) and specified temperature at the right boundary (node 5). The finite difference
formulation of the left boundary node (node 0) and the finite difference formulation for the rate of heat transfer at the right
boundary (node 5) are to be determined.
Assumptions 1 Heat transfer through the wall is given to be
steady and one-dimensional. 2 The thermal conductivity is
given to be constant.
Analysis Using the energy balance approach and taking the
direction of all heat transfers to be towards the node under
consideration, the finite difference formulations become
Left boundary node (all temperatures are in K):
0)2/()()( 00
01
0
4
0
4
surr =++
−
+−+− xAeAq
x
TT
kATThATTA
Heat transfer at right surface:
0)2/(
5
54
surfaceright =+
−
+xAe
x
TT
kAQ