Problem 5.150
The optimal way (from an energy standpoint) to transfer from one
circular orbit about a primary body
B
to another circular orbit is via
the so-called Hohmann transfer, which involves transferring from one
circular orbit to another using an elliptical orbit that is tangent to both
at the periapsis and apoapsis of the ellipse. The ellipse is uniquely
defined because we know
rP
(the radius of the inner circular orbit) and
rA
(the radius of the outer circular orbit), and therefore we know the
semimajor axis
a
by Eq. (5.88) and the eccentricity
e
by Eq. (5.87) or
Eqs. (5.90). Performing a Hohmann transfer requires two maneuvers,
the first to leave the inner (outer) circular orbit and enter the transfer
ellipse and the second to leave the transfer ellipse and enter the outer
(inner) circular orbit.
A spacecraft
S1
is transferring from circular low Earth parking
orbit with altitude
100 mi
to a circular orbit with radius
rA
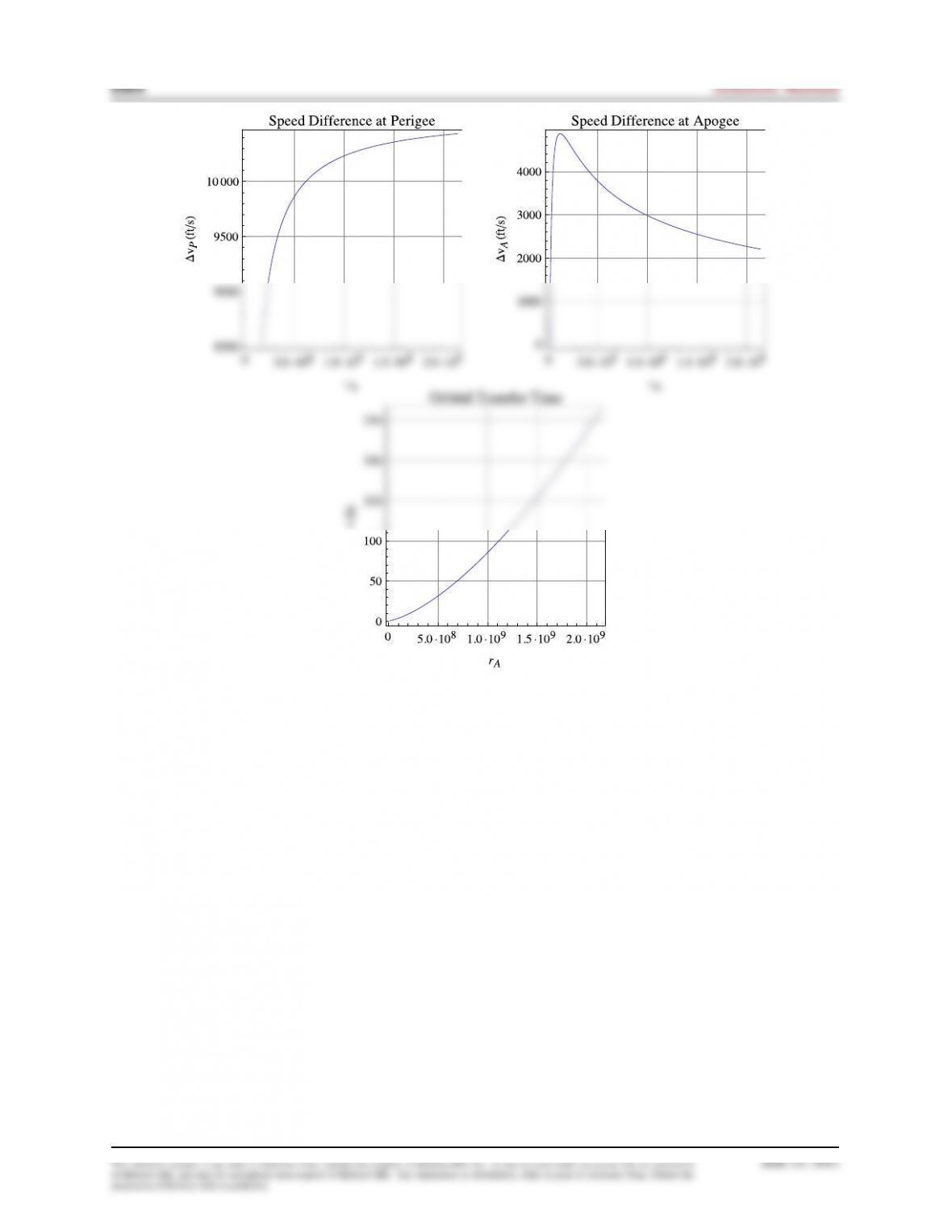
. Plot, as
a function of
rA
for
rPrA100rP
, the change in speed
vP
required at perigee of the elliptical transfer orbit, as well as the change
in speed
vA
required at apogee. In addition, plot the time as a
function of
rA
, again for
rPrA100rP
, required for the orbital
transfer. Assume that the changes in speed are impulsive; that is, they
occur instantaneously.
Next, let
v1
,
v2
,
v3
and
v4
denote the speeds of the satellite corresponding to the initial circular orbit, the
speed needed at perigee to move onto the the transfer orbit, the speed on the transfer orbit at apogee, and
e
reD3959 mi
is the radius of the Earth and
gD32:2 ft=s2
is the acceleration due to gravity on the surface of
the Earth. Hence, applying Eq. (2), we can determine the speeds v1,v2,v3and v4as follows:
e
e
of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the
permission of McGraw-Hill, is prohibited.