978-0073380308 Chapter 5 Solution Manual Part 22

1060 Solutions Manual

A disk

A

with mass

m

moves on a frictionless horizontal surface. The disk

is attached to point

O

with an elastic cord. The disk follows the trajectory

shown between

¿

and

¡

. The coordinates of

A

at

¿

and

¡

are

.x1;y

1/D

.1:5; 5:0/ cm

and

.x2;y

2/D.4:0; 3:0/ cm

, respectively. If the velocity of

A

at

¿

is parallel to the

y

axis and has a magnitude

v1D2:0 m=s

, determine

v2, the speed of Aat ¡, knowing that ✓D35ı.

Solution

where Erand Evare the position and velocity of A, respectively.

Force Laws. All forces are accounted for on the FBD.

Dynamics 2e 1061

Problem 5.135

A sphere of mass

m

slides over the outer surface of a cone with angle



and height

h

. The sphere was released at a height

h0

with a velocity of

magnitude

v0

and a direction that was completely horizontal. Assume

that the opening angle of the cone and the value of

v0

are such that

the sphere does not separate from the surface of the cone once put in

motion. In addition, assume that the friction between the sphere and the

cone is negligible. Determine the vertical component of the sphere’s

velocity as a function of the vertical position

´

(measured from the base

of the cone), v0,h,h0, and .

Solution

where Vis the potential energy of the system, and where, denoting the speed of the particle by v,

T1D1

2mv2

1and T2D1

2mv2

2:(3)

Force Laws. Choosing the datum for gravity to be at ´D0, we have

v2

2D.1 Ctan2/v2

´C✓hh0

h´◆2

v2

0:(13)

Substituting Eqs. (3), (4), the last of Eqs. (8), and Eq. (13) into Eq. (3), we have

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.

Dynamics 2e 1063

Problem 5.136

Consider a planet orbiting the Sun, and let

P1

,

P2

,

P3

, and

P4

be

the planet’s position at four corresponding time instants

t1

,

t2

,

t3

,

and

t4

such that

t2t1Dt4t3

. Letting

O

denote the position

of the Sun, determine the ratio between the areas of the orbital

sectors

P1OP2

and

P3OP4

.Hint: The area of triangle

OAB

defined by the two planar vectors

Ec

and

E

d

as shown is given by

Area(OAB)DjEc⇥E

dj.

Solution

t1Er⇥mEvdt DZt4

t3Er⇥mEvdt; (2)

for any two time intervals

t1tt2

and

t3tt4

such that

t2t1Dt4t3

, i.e., for any two time

intervals of equal duration. Since mis constant, Eq. (2) can be simplified to

Zt2

Problem 5.137

Using the lengths shown, as well as the property of an ellipse that

states that the sum of the distances from each of the foci (i.e., points

O

and

B

) to any point on the ellipse is a constant, prove Eq. (5.93),

that is, that the length of the semiminor axis can be related to the

periapsis and apoapsis radii via bDprPrA.

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.

Dynamics 2e 1065

Problem 5.138

Using the last of Eqs. (5.102), along with Eq. (5.103), solve for the eccentricity

e

as a function of

E

,



,

and GmB.

(a)

Using that result, along with fact that

e0

, show that

E<0

corresponds to an elliptical orbit,

ED0

corresponds to a parabolic trajectory, and E>0corresponds to a hyperbolic trajectory.

(b) Show that for eD0, the expression you found for eleads to Eq. (5.82).

Solution

We start by repeating here for convenience Eqs. (5.102) (on p. 391 of the textbook), Eq. (5.103) (on p. 391 of

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.

In addition, since the orbit is circular, the semimajor

a

axis coincides with the orbit’s radius, so that we have

aDrcDrP, which allows us to write

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.

Dynamics 2e 1067

Problem 5.139

Assuming that the Sun is the only significant body in the solar system (the mass of the Sun accounts for

99.8% of the mass of the solar system), determine the escape velocity from the Sun as a function of the

distance

r

from its center. What is the value of the escape velocity (expressed in km/h) when

r

is equal to

the radius of Earth’s orbit? Use

1:989⇥1030 kg

for the mass of the Sun and

150⇥106km

for the radius of

Earth’s orbit.

rD150⇥106km D150⇥109m. Therefore, the escape velocity of Earth is

.vesc/Earth D4:207⇥104m=sD151;500 km=h:

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.

Problem 5.140

The S-IVB third stage of the Saturn V rocket, which was used

for the Apollo missions, would burn for about

2:5 min

to place

the spacecraft into a “parking orbit.” Then, after several orbits, it

would burn for about

6min

to accelerate the spacecraft to escape

velocity to send it to the Moon. Assuming a circular parking orbit

with an altitude of

170 km

, determine the change in speed needed

at

P

to go from the parking orbit to escape velocity. Assume that

the change in speed occurs instantaneously so that you need not

worry about changes in orbital position during the engine thrust.

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.

Dynamics 2e 1069

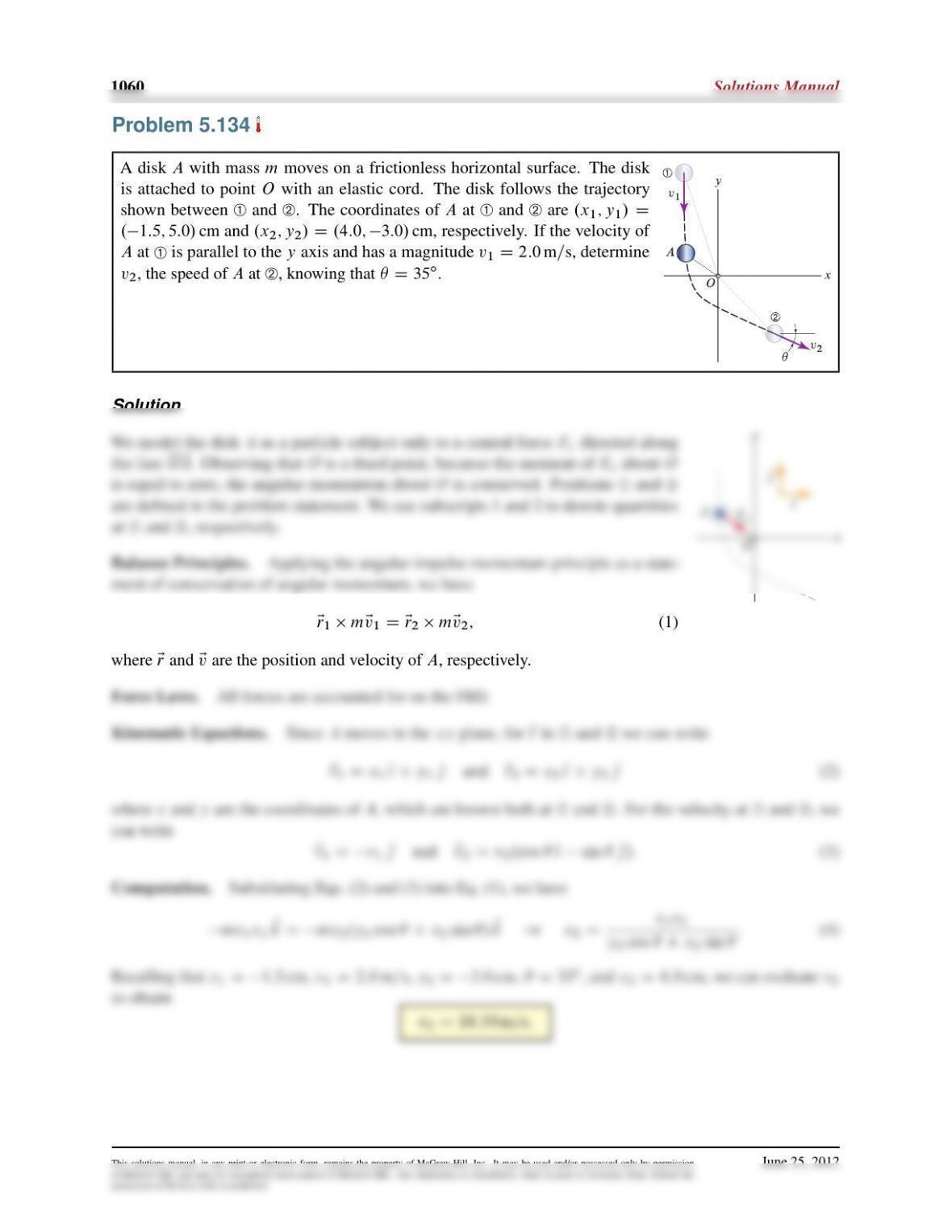
Problem 5.141

In 1705, Edmund Halley (1656–1742), an English astronomer, claimed that the comet sightings of 1531,

1607, and 1682 were all the same comet. He predicted this comet would return again in 1758. Halley did

not live to see the comet’s return, but it did return late in 1758 and reached perihelion in March 1759. In

honor of his prediction, this comet was named “Halley.” Each elliptical orbit of Halley is slightly different,

but the average value of the semimajor axis

a

is about

17:95 AU

. Using this value, along with the fact that

its orbital eccentricity is

0:967

(the orbit is drawn to scale, but the Sun is shown to be 36 times bigger than

it should be), determine

(a) the orbital period in years of Halley’s comet, and

(b)

its distance, in AU, from the Sun at perihelion

P

and at aphelion

A

. Look up the orbits of the planets

of our solar system on the Web. What planetary orbits is Halley near to at perihelion and aphelion?

Use 1:989⇥1030 kg for the mass of the Sun.

365 days.

Part (b).

Let the distances from the Sun at

P

and

A

be denoted by

rP

and

rA

, respectively. We can

of McGraw-Hill, and must be surrendered upon request of McGraw-Hill. Any duplication or distribution, either in print or electronic form, without the

permission of McGraw-Hill, is prohibited.